基于可能度的區間直覺模糊數排序方法及其在決策中的應用

魏艷艷，陳子春,徐福成

(西華大學數學與計算機學院，四川 成都 610039)

1986年，保加利亞學者Atanassov[1]對模糊集進行了拓展，把僅考慮隸屬度的模糊集推廣到同時考慮隸屬度、非隸屬度和猶豫度3個方面信息的直覺模糊集[2]，它在處理模糊性和不確定性等實際問題方面更具靈活性和實用性。目前直覺模糊集理論已被廣泛應用于決策、模式識別、機器學習、醫療診斷、市場預測等領域，取得了豐碩的研究成果[3-13]。由于直覺模糊集的隸屬度與非隸屬度有時很難用精確的數值來表達，Atanassov和Gargov又對直覺模糊集進行推廣，提出了區間直覺模糊集[3],同時定義了區間直覺模糊集的一些基本運算法則。文獻[4]定義了區間直覺模糊數概念，提出了區間直覺模糊加權平均算子與幾何算子，并通過引入區間直覺模糊的得分函數和精確函數，給出了一種基于區間直覺模糊信息的決策方法。進一步，文獻[5-6]給出了區間直覺模糊加權與有序加權平均算子及混合平均算子、加權與有序加權幾何算子及混合幾何算子等。在區間直覺模糊信息環境下進行多屬性決策問題研究時，區間直覺模糊數的排序是前提。文獻[5]基于得分函數和精確函數給出了區間直覺模糊數的一種排列方法。最近，文獻[7]通過再引入隸屬不確定性指標和猶豫不確定性指標，給出了區間直覺模糊數的一種全序排列方法。

直覺模糊數的得分函數與精確函數分別表達的是隸屬度與非隸屬度的代數和與差，它們是一個確定的值。 區間直覺模糊數的隸屬度與非隸屬度不是一個確定值，而是落在某個區間,反映了隸屬度與非隸屬度的不確定性。 當用一些確定指標值, 比如得分函數、精確函數、隸屬不確定性指標和猶豫不確定性指標對區間直覺模糊數進行排序時，并不能夠體現區間直覺模糊數的這種不確定性；因此，本文提出一種用區間數表達的得分函數和精確函數定義，然后基于可能度引入區間直覺模糊數的一種新的排序方法，并基于這種新的排序，給出了區間直覺模糊信息環境下的多屬性決策方法。

1 區間直覺模糊集的基本知識

為了便于討論，下面介紹區間直覺模糊集的基本定義與運算性質。

定義1[2]設X為一非空論域，一個X上的直覺模糊集A定義為

A={|x∈X}

其中：函數μA:X→[0,1]與υA:X→[0,1]滿足：0≤μA(x)+υA(x)≤1,?x∈X；μA(x)和υA(x)分別表示元素x屬于直覺模糊集A的隸屬度和非隸屬度。πA(x)=1-μA(x)-υA(x)，通常稱為x屬于A的直覺模糊指標，表示x屬于A的不確定程度。

Xu等在文獻[8]中稱(μ,υ)為直覺模糊數，其中μ∈[0,1],υ∈[0,1],μ+υ≤1，給出了直覺模糊數α=(μ,υ)的得分函數S(α)=μ-υ和精確函數H(α)=μ+υ，并利用得分函數和精確函數給出了直覺模糊數的排序方法。

由于客觀事物的復雜性和不確定性，隸屬度與非隸屬度的值往往難以用精確的實數值來表達，而用區間數形式表達則比較適合；因此，Atanassov等[1-3]又對直覺模糊集進行了擴展，提出了區間直覺模糊概念。

定義2[3]設X為一非空論域，D[0,1]是[0,1]區間中所有閉子區間之集合。一個X上的區間直覺模糊集A定義為

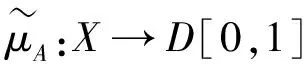
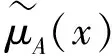
為了利用方便，徐澤水等在文獻[4-6]中稱序對([a,b],[c,d])是所謂的區間直覺模糊數，其中[a,b]?[0,1]，[c,d]?[0,1],b+d≤1，并給出了區間直覺模糊數的運算法則與集成方法，其中集成方法有區間直覺模糊加權與有序加權算術平均算子及混合平均算子、加權與有序加權幾何算子及混合幾何算子等，本文主要用到區間直覺模糊數的加權平均算子和加權幾何算子。

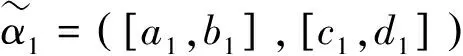
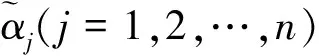
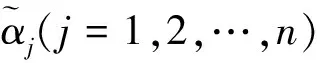
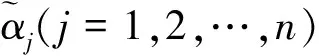
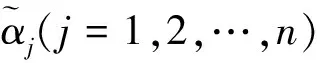
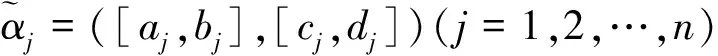
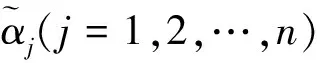
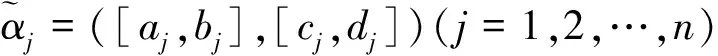
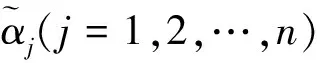
為了對區間直覺模糊數進行比較，以便得到滿足要求的最佳方案，徐澤水等在文獻[4]中給出區間直覺模糊數的得分函數和精確函數的定義。

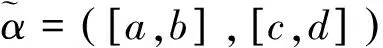
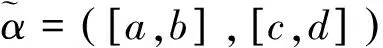
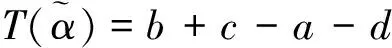
2 區間直覺模糊數的得分函數與精確函數

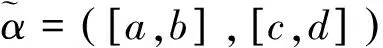
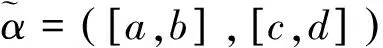
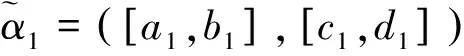
其中，μ是R×R上的面積測度。

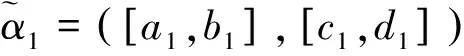
根據定義，容易得到：

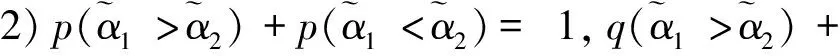
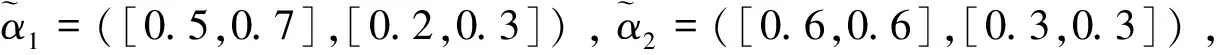
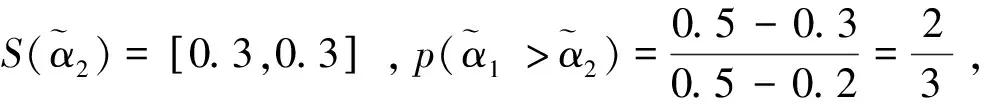
基于得分函數可能度和精確函數可能度，下面給出2個區間直覺模糊數的排序方法。

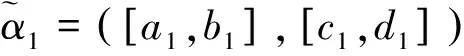
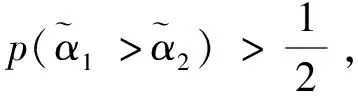
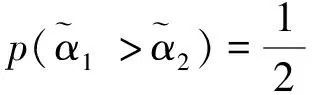
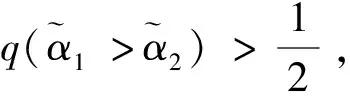
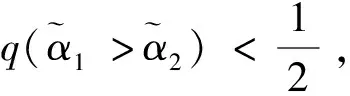
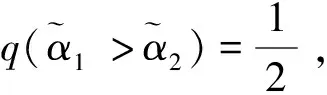
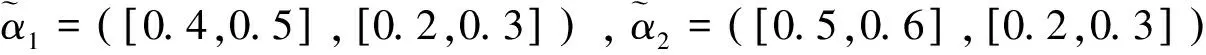
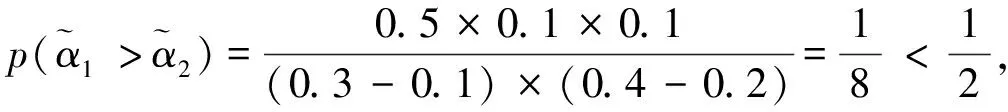
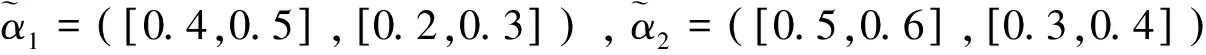
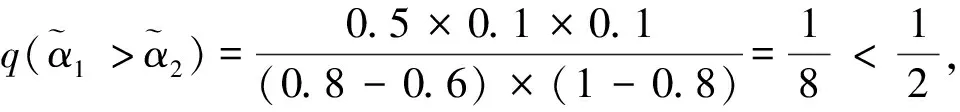
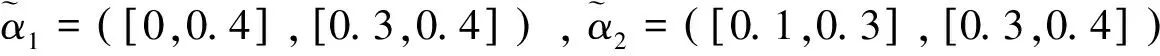
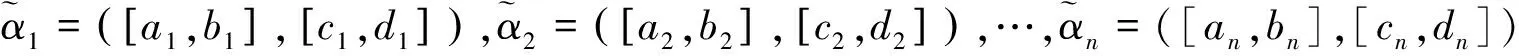
其中pij≥0,pij+pji=1,pii=0.5,i,j=1,2,…,n。稱p是得分函數互補矩陣。

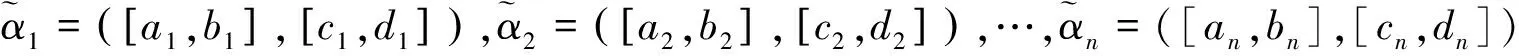
其中：qij≥0,qij+qji=1,qii=0.5,i,j=1,2,…,n。稱q是精確函數互補矩陣。

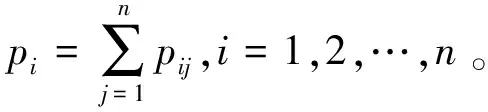
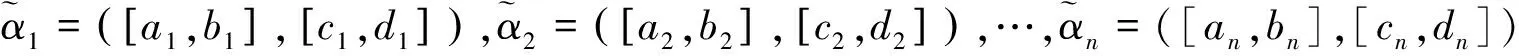
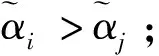
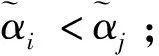
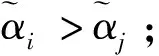
運用定義14給出的區間直覺模糊數的排序方法，下面給出一種基于加權平均算子和加權幾何算子下的區間直覺模糊多屬性決策法，具體如下：

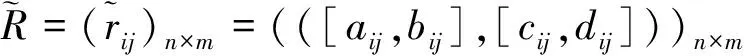
步驟1 利用區間直覺模糊數的加權平均算子

或加權幾何算子

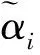
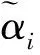
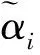
3 實例分析

下面利用一個投資決策問題來說明我們提出的方法的可行性和有效性。

假設一個基金經理在一個財富管理公司評估4個投資機會，X={x1,x2,x3,x4}。選擇每種投資機會都有4個屬性：冒險(a1)、增長(a2)、政治問題(a3)和環境因素(a4)，基金經理提供了各投資機會在各屬性下的評估信息，經過統計處理后可表示為區間直覺模糊數，決策矩陣[9]如下

這個矩陣中的每個元素都是一個區間直覺模糊數，代表了基金經理評估一種替代方案的隸屬度和非隸屬度。例如，矩陣的左上角的元素([0.42,0.48],[0.4,0.5])反映了基金經理認為在冒險(a1)遠景下選擇投資x1是優越的概率為42%～48%，不優越程度在40%～50%之間。假設基金經理提供出了各屬性的權重信息：ω1=0.150 0(冒險)，ω2=0.175 0(增長)，ω3=0.375 0(政治問題)，ω4=0.300 0(環境因素)。下面根據本文所給出的區間直覺模糊信息環境下的多屬性決策方法計算出4種投資機會的排序。

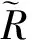
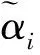
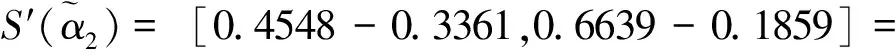
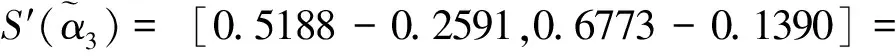
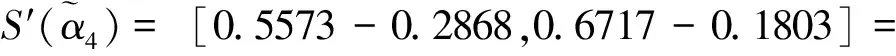
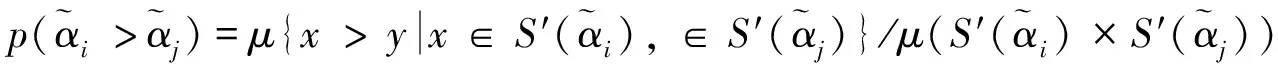
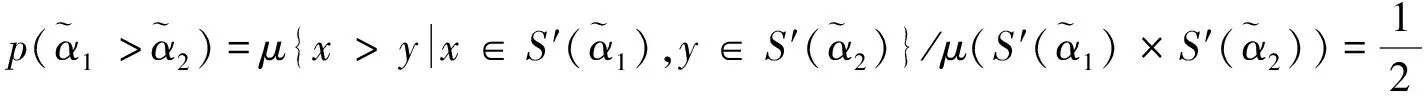
步驟4求得

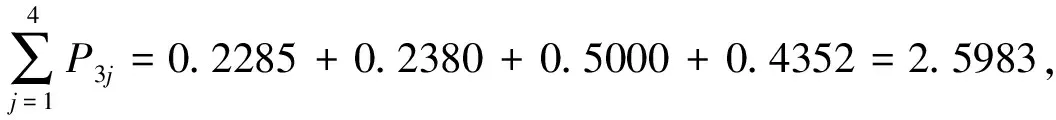
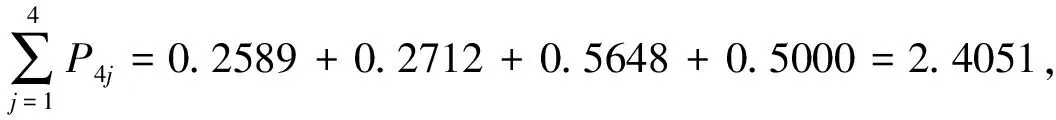
因此最終排序為x3?x4?x2?x1。

對于這個投資問題，利用加權平均算子得到的排序為x3?x4?x2?x1，利用幾何算子得到的排序為x4?x3?x2?x1，因此總的來說x3和x4是首要選擇，x1和x2作為次要選擇。

4 結束語

本文對模糊數問題進行了研究，為區間直覺模糊數提出了一種新的排序方法，該方法利用得分函數區間和精確函數區間求出得分函數可能度和精確函數可能度，然后對區間直覺模糊數進行排序。本文還給出了基于直覺模糊信息的一種新的決策方法，將區間直覺模糊決策矩陣轉化為區間數的決策矩陣，再運用得分函數區間的可能度求和得到排序。

[1]Atanassov K.Intuitionistic Fuzzy Sets[J].Fuzzy Sets and Systems, 1986，20: 87-96.

[2]Atanassov K.Intuitionistic Fuzzy Sets: Theory and Applications[M]. Heidelberg: Physica-Verlag, 1999.

[3]Atanassov K,Gargov G.Interval-valued Intuitionistic Fuzzy Sets[J]. Fuzzy Sets and Systems, 1989,31(3): 343-349.

[4]徐澤水.區間直覺模糊信息的集成方法及其在決策中的應用[J].控制與決策，2007, 22(2): 215-219.

[5]徐澤水，陳劍.一種基于區間直覺判斷矩陣的群決策方法[J].系統工程理論與實踐，2007, 27(4): 126-133.

[6]Xu Z S,Chen J.On Geometric Aggregation over Interval-valued Intuitionistic Fuzzy Information[C]//In Proceedings of the fourth international conference on fuzzy systems and knowledge discovery. Washington: IEEE Computer Society Press,2007: 466-471.

[7]Wang Z,Li K W, Wang W.An Approach to Multiattribute Decision Making with Interval-valued Intuitionistic Fuzzy Assessments and Incomplete Weights[J]. Information Sciencesg，2009,179: 3026-3040.

[8]Xu Z S, Yager R.Some Geometric Aggregations Based on Intuitionistic Fuzzy Sets[J]. International Journal of General Systems, 2006,35: 417-413.

[9]Herrera F,Herrera-Viedma E.Linguistic Decision Analysis: Steps for Solving Decision Problems under Linguistic Information[J].Fuzzy Sets and Systems,2000,115:67-82.

[10]Hsu S C, Wang T C.Solving Multi-criteria Decision Making with Incomplete Linguistic Preference Relations[J].Expert Systems with Applications,2011, 38:10882-10888.

[11]J W ,J B L.Some Programming Models to Derive Priority Weights from Additive Interval Fuzzy Preference Relation[J].Knowledge-Based Systems,2012,27:69-77.

[12]Z P.Rational Decision MakingModels with Incomplete Weight Informationfor Production Line Assessment[J].Information Sciences,2013,222:696-716.

[13]J W.Robust Optimization Analysis for Multiple Attribute Decision Making Problems with Imprecise Information[J].Annals of Operations Research,2012, 197:109-122.