帶二階Hermite插值條件的最小二乘估計(jì)

(西華大學(xué)數(shù)學(xué)與計(jì)算機(jī)學(xué)院, 四川 成都 610039)

插值，即構(gòu)造函數(shù)使得已知點(diǎn)能最大程度的滿足某種函數(shù)關(guān)系，通過構(gòu)造已知點(diǎn)和點(diǎn)之間的某種內(nèi)在規(guī)律的數(shù)量關(guān)系，進(jìn)而推測(cè)未知點(diǎn)的性質(zhì)。在現(xiàn)實(shí)生活中，我們的研究通常是基于有限樣本數(shù)據(jù)，且已知的這些數(shù)據(jù)也很可能不會(huì)恰好滿足已知的某個(gè)函數(shù)。插值法就是構(gòu)造函數(shù)，從而揭示樣本數(shù)據(jù)間的內(nèi)在規(guī)律的方法。

常見的插值法有：Lagrange插值、Newton插值多項(xiàng)式、Hermite插值、分段低次插值、三次樣條插值[1-7]。每種插值法都有其優(yōu)缺點(diǎn)。Lagrange插值結(jié)構(gòu)緊湊、思想清晰、顯式表示、公式對(duì)稱，與插值節(jié)點(diǎn)的編號(hào)無關(guān)，適合理論分析；但是該方法無承襲性。Newton插值法既有Lagrange插值公式便于理論分析的優(yōu)點(diǎn)，又具有承襲性，從而在需要增加節(jié)點(diǎn)時(shí)，可大大減少計(jì)算量；然而該法只是Lagrange插值公式的一種變形[8-11]。Hermite插值作為顯式算法，簡(jiǎn)單且收斂性、穩(wěn)定性好，而且具有局部性，即如果要修改某個(gè)數(shù)據(jù)，插值曲線僅僅在某個(gè)局部范圍內(nèi)受到影響，而代數(shù)插值卻會(huì)影響到整個(gè)插值區(qū)間；然而該法光滑性不高，若要提高光滑度，必須提供較多的信息才能達(dá)到。分段三次Hermite插值比分段線性插值效果明顯要好，但其要求給出節(jié)點(diǎn)上的導(dǎo)數(shù)值，所要提供的已知信息變多，其光滑度也不高，只有一階導(dǎo)數(shù)連續(xù)。三次樣條插值具有良好的收斂性與穩(wěn)定性，又有二階光滑性，理論上和實(shí)際都有重要意義。

實(shí)際工作中，變量間未必都有線性關(guān)系，如服藥后血藥濃度與時(shí)間的關(guān)系、疾病療效與療程長(zhǎng)短的關(guān)系、毒物劑量與致死率的關(guān)系等常呈曲線關(guān)系。曲線擬合是指選擇適當(dāng)?shù)那€類型來擬合觀測(cè)數(shù)據(jù)，并用擬合的曲線方程分析兩變量間的關(guān)系。已知數(shù)據(jù)通常本身不一定可靠，個(gè)別數(shù)據(jù)的誤差甚至可能遠(yuǎn)遠(yuǎn)大于已知數(shù)據(jù)，不妨記樣本數(shù)據(jù)點(diǎn)為(xk,yk),k=1,2,…，n，并稱為擬合點(diǎn)。最小二乘法在工業(yè)技術(shù)和其他科學(xué)研究中有廣泛應(yīng)用。如果還要求擬合曲線必須經(jīng)過另外s個(gè)點(diǎn)(xk,yk),k=1,2,…,s，那么這s個(gè)點(diǎn)就稱為插值點(diǎn),文獻(xiàn)[1-5]中討論了帶插值條件的最小二乘法,文獻(xiàn)[6]系統(tǒng)地闡述了最小二乘法。本文將在插值條件的基礎(chǔ)上,增加滿足一階導(dǎo)數(shù)和二階導(dǎo)數(shù)條件的要求,即二階Hermite插值條件。下面給出帶二階Hermite插值條件的最小二乘法的定義。

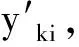
1 主要結(jié)果及證明

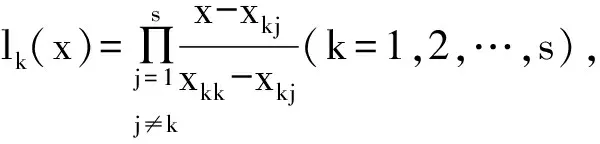
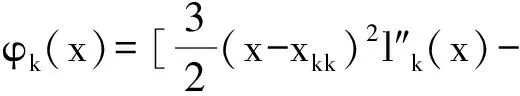
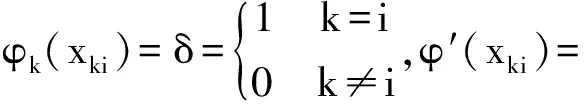
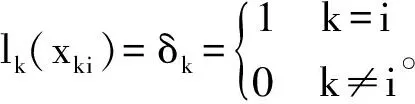
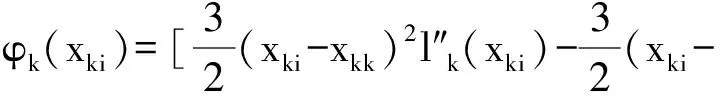
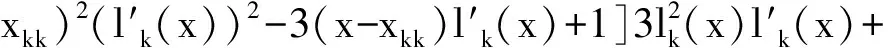
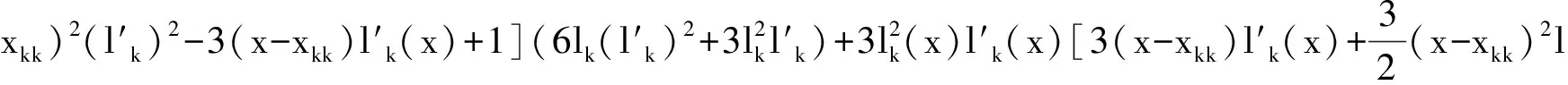
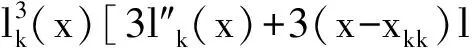
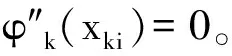
同理可證

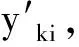
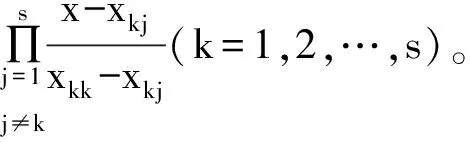
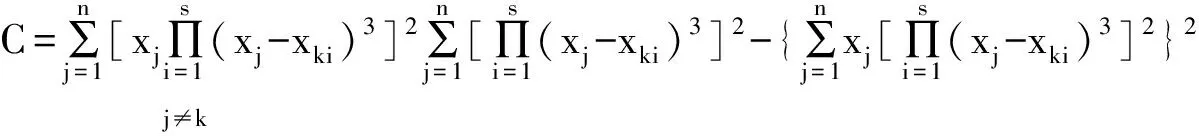
(2)

其中:

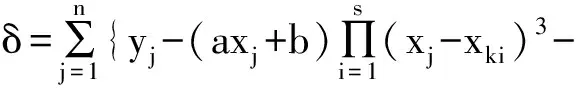
若將δ看作關(guān)于自變量a、b的二元函數(shù)，則上述問題轉(zhuǎn)化為求函數(shù)δ=δ[a,b]在哪些點(diǎn)取得最小值。即解方程組

(3)

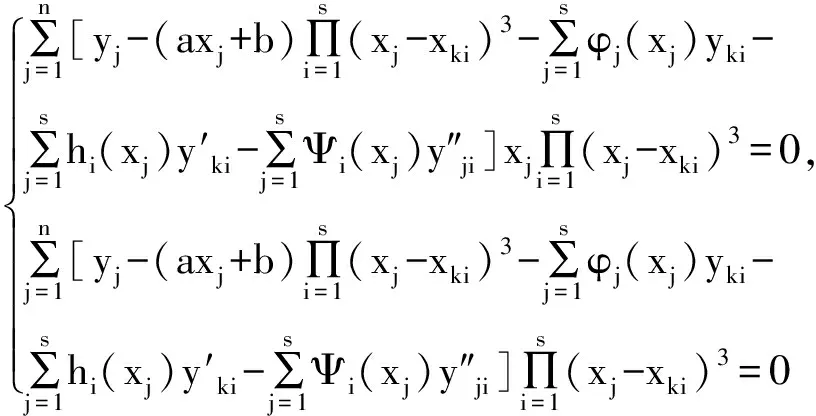
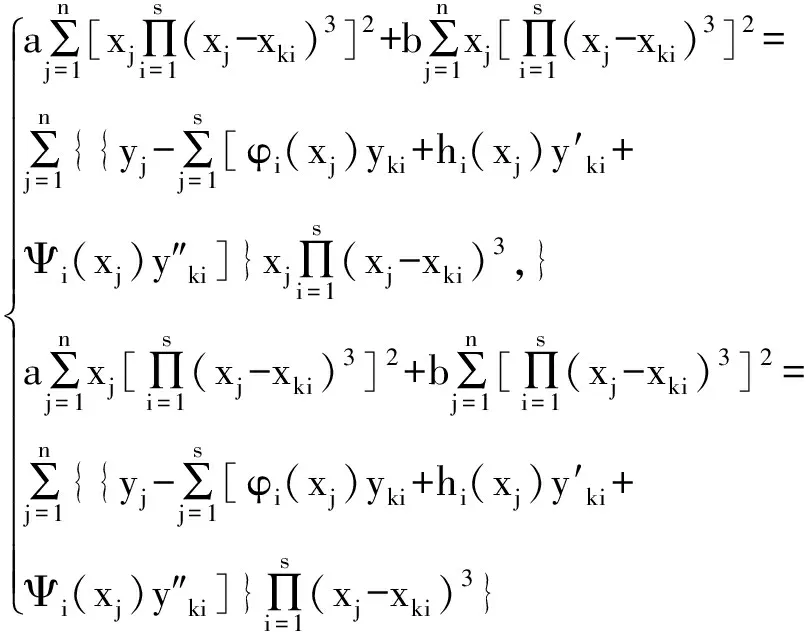
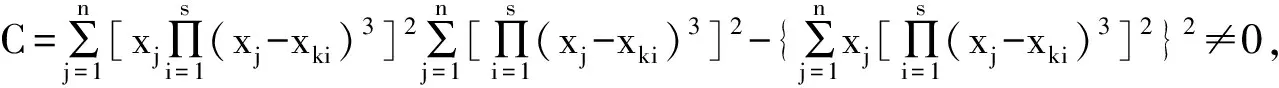
故方程組的解為

(4)

經(jīng)過帶二階Hermite插值條件的最小二乘法的擬合，使得曲線的擬合效果更好。

2 Lingo程序設(shè)計(jì)

設(shè)n為需要擬合的點(diǎn)的個(gè)數(shù)，k為滿足插值點(diǎn)、一階導(dǎo)數(shù)點(diǎn)、二階導(dǎo)數(shù)點(diǎn)的個(gè)數(shù)，s-1是需要尋找的擬合曲面的次數(shù)，則帶n個(gè)擬合點(diǎn)、k個(gè)插值點(diǎn)、k個(gè)一階導(dǎo)數(shù)點(diǎn)及k個(gè)二階導(dǎo)數(shù)點(diǎn)的s-1次曲線擬合的Lingo程序如下：

model:

sets:

shuju/1..n/:x,y;

chazhi/1..k/:a,b,c,d,e,f;

xishu/1..s/:z;

endsets

data:

x=?;!輸入擬合點(diǎn)數(shù)據(jù);

y=?;

a=?;!輸入插值點(diǎn)數(shù)據(jù);

b=?;

c=?;!輸入一階導(dǎo)數(shù)點(diǎn)數(shù)據(jù);

d=?;

e=?;!輸入二階導(dǎo)數(shù)點(diǎn)數(shù)據(jù);

f=?;

enddata

min=@sum(shuju:(z(s)*x^(s-1)+z(s-1)*x^(s-2)+..+z(2)*x+z(1)-y)^2);

@for(chazhi:z(s)*a^(s-1)+z(s-1)*a^(s-2)+..+z(2)*a+z(1)=b);

@for(chazhi:(s-1)*z(s)*c^(s-2)+(s-2)*z(s-1)*c^(s-3)+..+2*z(3)*c+z(2)=d);

@for(chazhi:(s-1)*(s-2)*z(s)*e^(s-3)+(s-2)*(s-3)*z(s-1)*e^(s-4)+...+2*z(3)=f);

@free(z(i));(i>1)

end

示例

擬合點(diǎn)357 9 26.3 25.724.823.9插值點(diǎn)126.8一階導(dǎo)數(shù)點(diǎn)1-1二階導(dǎo)數(shù)點(diǎn)1-5

model:

sets:

shuju/1..4/:x,y;

chazhi/1..1/:a,b,c,d,e,f;

xishu/1..4/:z;

endsets

data:

x=3 5 7 9;

y=26.3 25.7 24.8 23.9;

a=1;

b=26.8;

c=1;

d=-1;

e=1;

f=-5;

enddata

min=@sum(shuju:(z(4)*x^3+z(3)*x^2+z(2)*x+z(1)-y)^2);

@for(chazhi:z(4)*a^3+z(3)*a^2+z(2)*a+z(1)=b);

@for(chazhi:3*z(4)*c^2+2*z(3)*c+z(2)=d);

@for(chazhi:6*z(4)*e+2*z(3)=f);

@free(z(1));

@free(z(2));

@free(z(3));

@free(z(4));

end

運(yùn)行結(jié)果

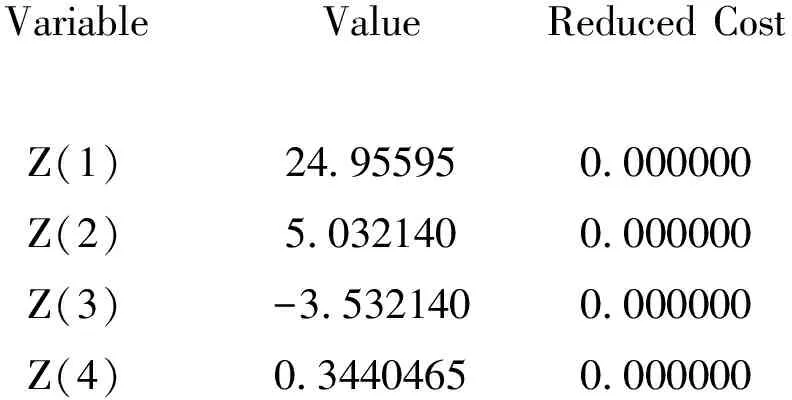
VariableValueReduced CostZ(1)24.955950.000000Z(2)5.0321400.000000Z(3)-3.5321400.000000Z(4)0.34404650.000000

[1]顏寧生. 帶Hermite插值條件的最小二乘估計(jì)[J].大學(xué)數(shù)學(xué)學(xué)報(bào): 2011, 27(5) : 80-84.

[2]顏寧生. 帶插值條件的最小二乘法[J].北京服裝學(xué)院學(xué)報(bào): 2007, 27(2) : 42-48.

[3]顏寧生. 帶一個(gè)插值點(diǎn)的最小二乘估計(jì)和最大似然估計(jì)[J].北京服裝學(xué)院學(xué)報(bào)， 2008, 28(3) : 56-59.

[4]張光遠(yuǎn), 李慶福, 顏寧生. 帶Hermite 插值條件下的三點(diǎn)曲線擬合[J].溫州職業(yè)技術(shù)學(xué)院學(xué)報(bào), 2009, 9(4) : 61- 63.

[5]顏寧生. 帶一個(gè)插值點(diǎn)的回歸模型的參數(shù)分析[J].高等數(shù)學(xué)研究, 2010, 13(4) : 6- 8.

[6]賈小勇, 徐傳勝, 白欣. 最小二乘法的創(chuàng)立及思想方法[J].西北大學(xué)學(xué)報(bào):自然科學(xué)版, 2006, 36(3) : 507 -511.

[7]Liu Guangpu, Gao Yuchun.The Application of MATLAB in Communication Theory [J]. Procedia Engineering, 2012, 28(3)：321-324.

[8]吉家鋒,張曉麗,謝維成.用MATLAB計(jì)算等距三次樣條插值問題[J].四川工業(yè)學(xué)院學(xué)報(bào),2003(S1): 37-40.

[9]劉衛(wèi)國.MATLAB程序設(shè)計(jì)與應(yīng)用[M].2版.北京：高等教育出版社，2006.

[10]張德豐.MATLAB程序設(shè)計(jì)與典型應(yīng)用[M].北京：電子工業(yè)出版社，2009.

[11]李海濤. MATLAB程序設(shè)計(jì)教程[M].北京：高等教育出版社，2010.