基于改進遺傳算法的滿堂支架傳感器優化布置
韓大勇,李建宇,呂貴賓
(1.中電建路橋集團有限公司,北京100048; 2.中水電鄭州投資發展有限公司,河南鄭州450000)
近幾年,橋梁工程建設數量與日俱增。在橋梁工程建設中,可根據橋型、橋址地理位置等因素采用不同的橋梁建設施工方法,較常采用的方法有懸臂施工法和支架法施工。在滿堂支架法施工過程中,由于支架桿件數量巨大、桿件受力復雜,對其進行穩定性監測時,傳感器的最合理布置方案成為一個需認真考慮分析的問題。如何利用盡可能少的傳感器來獲取滿堂支架最可靠、最全面的受力信息和穩定性狀態,就是傳感器優化布置的主要目的[1]。
遺傳算法起源于達爾文的生物進化理論,生物進化的動力和機制在于自然選擇,自然選擇是用變異做材料,通過生存斗爭實現的。凡是具有適應環境的有利變異個體,在生存斗爭中將有更多機會生存和繁殖后代,而適應性較小的個體將被淘汰,因此,生物進化便是“物競天擇,適者生存”的過程[2]。
遺傳算法的兩大特點是群體搜索策略和解群中串之間的信息相互交叉。其基本過程為:首先隨機的產生一些個體組成初始種群(population)(即問題的一群候選解),按預先根據目標函數確定的適應度函數計算各個體對問題函數的適應度(fitness),再根據個體適應度對個體對應的染色體進行選擇(selection),抑制適應度低的染色體,弘揚適應度高的染色體,然后借助于遺傳算子進行交叉(crossover)和變異(mutation)產生進化了的一代群體。如此反復,不斷向更優解方向進化,最后得到滿足某種終止條件的最適應問題環境的群體,其中的最優個體經過解碼(decoding)而獲得問題的最優解。
本文將傳統的遺傳算法進行改進,并應用改進的遺傳算法對一個實例橋梁工程所搭設的滿堂支架進行了傳感器優化布置方案計算。計算結果表明,改進的遺傳算法可更好的滿足滿堂支架傳感器優化布置計算的需要,計算效率大大提高,有較高的實用價值。
1 改進遺傳算法
基本遺傳算法(Simple Genetic Algorithm,SGA)是指采用比例選擇、單點交叉和基本位變異算子的遺傳算法,其遺傳過程簡單,容易理解,是其它遺傳算法的雛形和基礎,為其它各種遺傳算法提供了基本框架。
本文在傳統遺傳算法的基礎上對其進行改進和優化[3],具體的優化改動有:
1.1 二重結構編碼
二重結構編碼方法如表 1所示。個體染色體表示的二重結構由變量碼和附加碼兩行組成。上行s(i)為變量xj的附加碼s(i)=j,下行為變量xs(i)對應于附加碼s(i)的值。
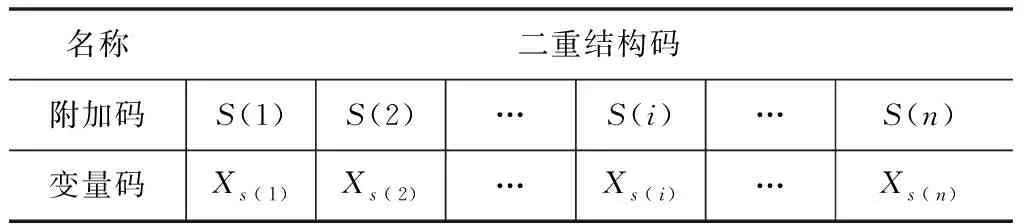
表 1 二重結構編碼
對某個個體編碼時,首先按洗牌方式隨機產生附加碼{s(i),(i=1,…,n)},列于上行;然后隨機產生下行的變量碼值(0或1),這樣構成一個個體的二重結構編碼。
個體解碼時,需要考慮約束條件。如表 2所示,按照從左到右的順序,依次考慮變量的附加碼,即按順序考慮附加碼為s(i)的物件,如果處理到某個物件時違背了約束條件,強制使該物件的變量值ps(i)為1,直到所有物件都處理完為止。
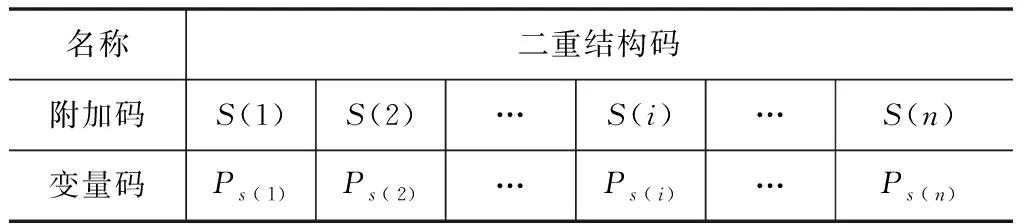
表 2 二重結構解碼
解碼算法的步驟如下:
第1步i=1,sum=0。
第2步 若xs(i)=0,則ps(i)=0,執行第4步,否則,執行第3步。
第3步 若sum+as(i)≤b,則ps(i)=1,sum=sum+as(i),否則ps(i)=0。
第4步i=i+1,若i≤n,返回到第3步,否則終止。
例如:從10個節點中選擇4個節點布置傳感器,如果隨機產生的附加碼和變量碼序列如表 3所示,它對應于一個可行解,即選擇了序號2,1,4,3的節點。

表3 一個個體的二重結構編碼與解碼
1.2 部分匹配交叉
部分匹配交叉步驟如下:
(1)隨機選取兩個交叉點i,j,i≠j,若i>j,則i?j;
(2)交換兩個父個體交叉點i、j之間的匹配段;
(3)對子個體1、子個體2中的兩端部分,分別保留從其父個體中繼承未選擇的編碼;
(4)對子個體1、子個體2中的兩端部分,若從其父個體中繼承的編碼與交換后中間段編碼出現重復,則根據父個體中間段的映射關系決定所取編碼。如果映射關系中存在傳遞關系,即備選交換有多個碼,則選擇此前未確定的一個碼作交換。
本操作只針對個體的上行附加碼進行,子個體的下行變量碼順序不變。
兩個個體X,Y經過部分匹配交叉操作后產生的兩個子個體X*、Y*的情況如圖1所示。

附加碼31561098724變量碼0110001101X附加碼12734659108變量碼1100100011Y

附加碼X1X346572X變量碼0110001101附加碼12761098XXX變量碼1100100011

附加碼91834657210變量碼0110001101X附加碼12761098345變量碼1100100011Y
圖1 二重結構部分區配交叉
1.3 逆位變異
二重結構編碼的變異操作采用逆位變異算子,即對父個體隨機產生兩個變異點,兩點間的上行附加碼按相反順序重新排列,而下行的變量碼順序不變,如圖 2所示。

附加碼31561098724變量碼0110001101X

附加碼31589106724變量碼0110001101X*
圖2 逆位變異
1.4 自適應交叉變異
遺傳算法參數中交叉概率pc和變異概率pm的選擇是影響遺傳算法行為和性能的關鍵所在,直接影響算法的收斂性。自適應遺傳算法中pc和pm隨適應度自動改變,當適應度值低于平均適應度值時,說明該個體是性能不好的個體,對它采用較大的交叉率和變異率;如果適應度值高于平均適應度值,說明該個體性能優良,對它就根據其適應度值取較小的交叉率和變異率,在保持群體多樣性的同時,又保證了遺傳算法的收斂性。pc和pm的計算表達式見式(1)、(2):
(1)
(2)
式中:pc1=0.9,pc2=0.6,pm1=0.1,pm2=0.001,其中pc1~pc2和pm1~pm2為經驗的取值范圍。fmax為群體中最大的適應度值;favg為每代群體的平均適應度值;f1為要交叉的兩個個體中較大的適應度值;f2為要變異個體的適應度值。
2 算法實現
本文以鄭州市三環路快速化工程為研究背景,對其建設過程中使用的滿堂支架系統進行了傳感器優化布置計算。以滿堂支架桿件縱橋向位移傳感器最優測點選擇為例,采用工具軟件MATLAB進行改進遺傳算法的實現。
(1)根據滿堂支架有限元計算結果,選取縱橋向位移較大的6根桿件進行分析。即橫橋向從北向南數第8排(箱梁腹板下方),縱橋向從東向西數第2根(5#橋墩附近)、10根(1/4跨徑)、18根(跨中附近)、19根(跨中附近)、28根(1/4跨徑)、37根(4#橋墩附近),對各桿件節點進行編號,共有78個節點,如圖 3所示。
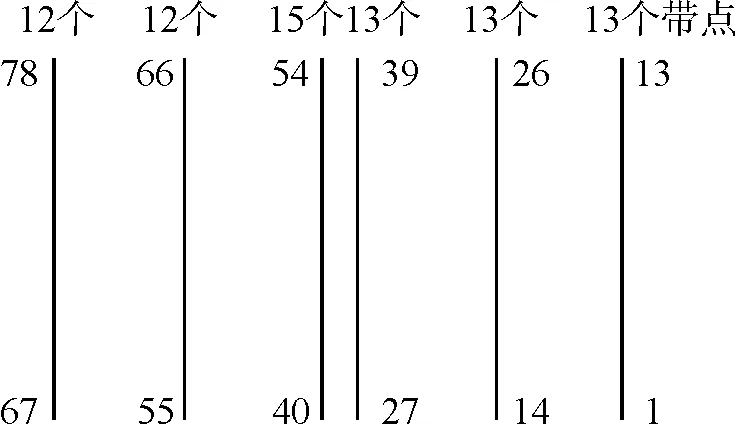
圖 3 節點選取示意
(2)從滿堂支架ANSYS有限元計算結果中導出上述節點各施工階段縱橋向位移值,作為模態參數,用于適應度函數的計算。
(3)設置改進遺傳算法初始參數,從78個候選位置選取12個節點布置縱向位移傳感器,MATLAB中的參數查看窗口如圖 4所示。

圖 4 遺傳算法基本參數
(4)將上述數據輸入MATLAB軟件中,結果如圖5所示。
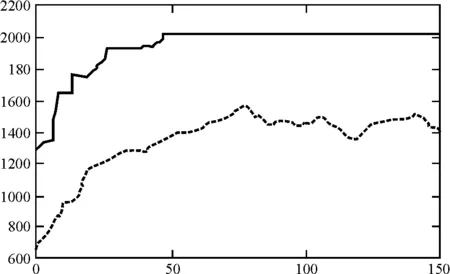
圖 5 傳感器布置算法收斂過程及結果
圖5中,上曲線為最優個體適應度值,下曲線為種群平均適應度值,由曲線變化可見改進遺傳算法以較好的概率得到最優解。
由圖 6可得,各傳感器的最優布置位置。
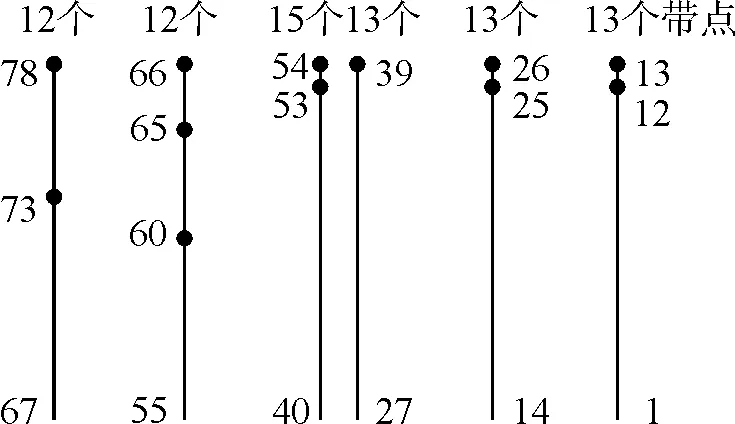
圖 6 傳感器布置示意
通過調整遺傳算法計算參數,可得到布置不同個傳感器時的具體位置,可為滿堂支架傳感器的現場選型與安裝提供理論參考。
3 結論
從實際工程需求出發,本文對采用改進遺傳算法進行滿堂支架傳感器優化布置進行了實踐,得到如下結論:
(1)改進遺傳算法用于滿堂支架傳感器優化布置,相比于傳統遺傳算法效率更高,滿足工程計算的需要。
(2)通過對實際工程進行傳感器優化布置的計算可知,運用改進遺傳算法進行滿堂支架傳感器布置方案優化,可利用較少的傳感器把握滿堂支架整體受力信息,具有較好的經濟效益。
[1] 王振華. 大跨度鐵路鋼桁斜拉橋傳感器優化布置研究[D]. 成都: 西南交通大學, 2011
[2] 李戈, 秦權, 董聰. 用遺傳算法選擇懸索橋監測系統中傳感器的最優布點[J]. 工程力學, 2000, 17(2): 25-35
[3] 黃民水, 朱宏平, 李煒明. 基于改進遺傳算法的橋梁結構傳感器優化布置[J]. 振動與沖擊, 2008, 27(3): 82-86

