基于高斯混合模型的非高斯隨機振動幅值概率密度函數

程紅偉， 陶俊勇， 蔣 瑜， 陳 循

(1.國防科技大學 裝備綜合保障技術重點實驗室，長沙 410073;2.國防科技大學 機電工程與自動化學院，長沙 410073)

在工程實際中，一般基于高斯假設對機械振動信號進行統計分析和研究。但是，近來越來越多的學者注意到機械振動的高斯性假設在某些情況下是不成立的，機械隨機振動的非高斯特性開始受到關注。Steinwolf[1]研究了湍流邊界層在機翼蒙皮所引起振動的非高斯性。Gioffré[2]，Gurley[3]和董欣[4]分別研究了風引起的振動載荷的非高斯性。Rouillard[5]深入研究了車輛振動環境的非高斯性，并提出了一種基于計算機程序的高斯分解方法。Rychlik等[6-8]對海浪引起的振動載荷的非高斯性進行了大量的統計研究。

對于平穩非高斯振動信號，概率密度函數能夠全面地反映其統計特性，它決定了非高斯信號高階矩和高階累積量的大小。非高斯隨機信號幅值概率密度函數的數學描述，主要有Edgeworth展開法、高斯變換法和最大熵法。Harremoes[9]對比分析了最大熵法和Edgeworth展開法的優缺點。Winterstein[10]分析了Edgeworth展開法的缺點，并通過對高斯概率密度函數進行非線性變換，得到基于高斯變換法的非高斯概率密度函數。在隨機信號非高斯性較強的情況下，Edgeworth展開法得到的概率密度曲線會出現負值并呈現多峰態；而基于最大熵理論的方法也會使單峰的非高斯概率密度函數呈現多峰態[9]。高斯變換法的問題在于僅適用于一定的峭度范圍，并且該方法計算過程復雜[10]。另外，Steinwolf[11]提出了一種基于經驗信息的高斯曲線拼接法。Rouillard[5,12]提出了基于搜尋算法的高斯混合模型。高斯拼接法和Rouillard提出的高斯混合法，都能夠較好地逼近非高斯隨機振動信號概率密度函數。但是，這兩種方法計算量大，工程中應用困難。

綜上所述，針對非高斯振動信號的幅值概率密度函數，需要提出一種既能滿足計算精度要求，而計算過程又相對簡單的數學模型。在本研究中，我們基于高斯混合模型的數學思路，提出了基于非高斯振動信號高階統計量的高斯混合模型。應用該數學模型對仿真非高斯振動信號和實測非高斯振動信號的幅值概率密度進行表述，通過與經驗分布的對比驗證了該方法的有效性。通過與其它方法的對比，進一步驗證了該方法的正確性和工程應用價值。

1 非高斯振動

從理論上來說，能夠全面描述一個隨機過程非高斯特性的統計量和頻譜函數為：高階矩、高階累積量和高階譜[13-14]。但是由于隨機過程高階統計量和高階譜的復雜性，使其在非高斯振動領域難以開展工程應用。所以，研究人員大都借助隨機變量的高階統計量來描述平穩隨機過程的非高斯性，其中最常用的是標準化3階中心矩和標準化4階中心矩，即偏斜度γ3和峭度γ4[1,15-17]，

(1)

(2)

其中，X為非高斯隨機變量；μX和σX分別為X的均值和標準差；M3和M4分別為X的3階中心矩和4階中心矩，可由X的概率密度函數計算得到。需要注意的是，高斯隨機變量的偏斜度恒為0，峭度恒為3。

對于零均值平穩非高斯振動，通過時域樣本序列可以對其偏斜度和峭度進行估計，

(3)

(4)

其中，x(t)為隨機過程X(t)的樣本信號；T為樣本時間長度。

Rouillard[5]和Rizzi[18]分別對實際環境中的非高斯振動信號進行了大量的統計分析，并指出在實際振動環境中，很少存在嚴格意義上的平穩信號，所以大多隨機振動的非高斯性是由短時非平穩性造成的。然而，對于短時非平穩信號，從長時間的觀測序列來看，它具有平穩信號的特性。所以，在工程中對于宏觀平穩，而短時非平穩的振動信號一般都基于平穩隨機過程假設對其進行處理。

2 高斯混合模型

Middleton[19]在研究通信系統中多源疊加噪聲信號的幅值概率分布時提出了高斯混合模型，并在通信領域得到廣泛的應用。高斯混合模型的統一表達式為，

(5)

其中fNG為非高斯概率密度函數；fi(x)為第i個高斯分量的概率密度函數；αi為第i個高斯分量的權值，0 ≤αi≤ 1，∑αi=1。一般情況下，2、3階高斯混合模型就可以給出精度足夠高的非高斯概率密度函數[20]。在本研究中，我們采用2階高斯混合模型，

fNG(x)=αf1(x)+(1-α)f2(x)

(6)

根據Middleton提出的高斯混合模型理論，需要在全面掌握各噪聲源的物理特性的前提下，以Poisson分布來確定不同高斯分量的權值αi，這在機械振動信號處理中是不能實現的。

眾所周知，零均值高斯概率密度函數可以由標準差完全確定。所以零均值非高斯過程的二階高斯混合模型可以表示為：

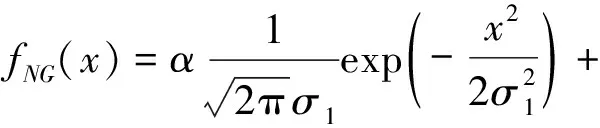
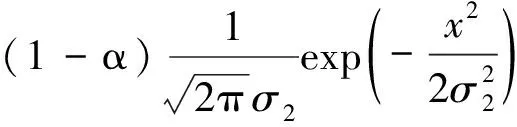
(7)

其中σ1和σ2分別為高斯分量1和高斯分量2的標準差；α和1-α分別為高斯分量1和高斯分量2的權值。式(7)中有三個未知量：σ1、σ2和α。

可以根據非高斯振動樣本信號來估計其2、4、6階中心矩，在零均值情況下中心矩和原點矩相同，

(8)

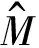
(9)

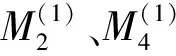
(10)

所以有，

(11)

將式(11)代入式(9)，得方程組：

(12)

以式(8)給出的樣本估計量代替真值，則有：

(13)

對于方程組(13)，通過科學計算軟件求解得到未知量α，σ1和σ2，將其代入式(7)中，得到給定非高斯振動信號的幅值概率密度函數。

3 示例

為了綜合驗證所提出的高斯混合模型的有效性，這里給出了兩個示例的詳細計算過程：

(1)峭度較低的仿真非高斯振動信號；

(2)峭度較大的實測車輛振動信號。

最后，通過對4個振動信號(兩個仿真信號，兩個實測信號，進行誤差分析，從定量的角度來驗證高斯混合模型的準確性和有效性。

3.1 仿真信號

引入一個對稱分布的非高斯仿真信號，如圖1所示。該仿真信號的均值為0，方差為1.1976 × 103，偏斜度為0，峭度為8.1394。圖1(a)為信號的時域序列；圖1(b)為功率譜密度，該振動信號是寬帶非高斯信號。

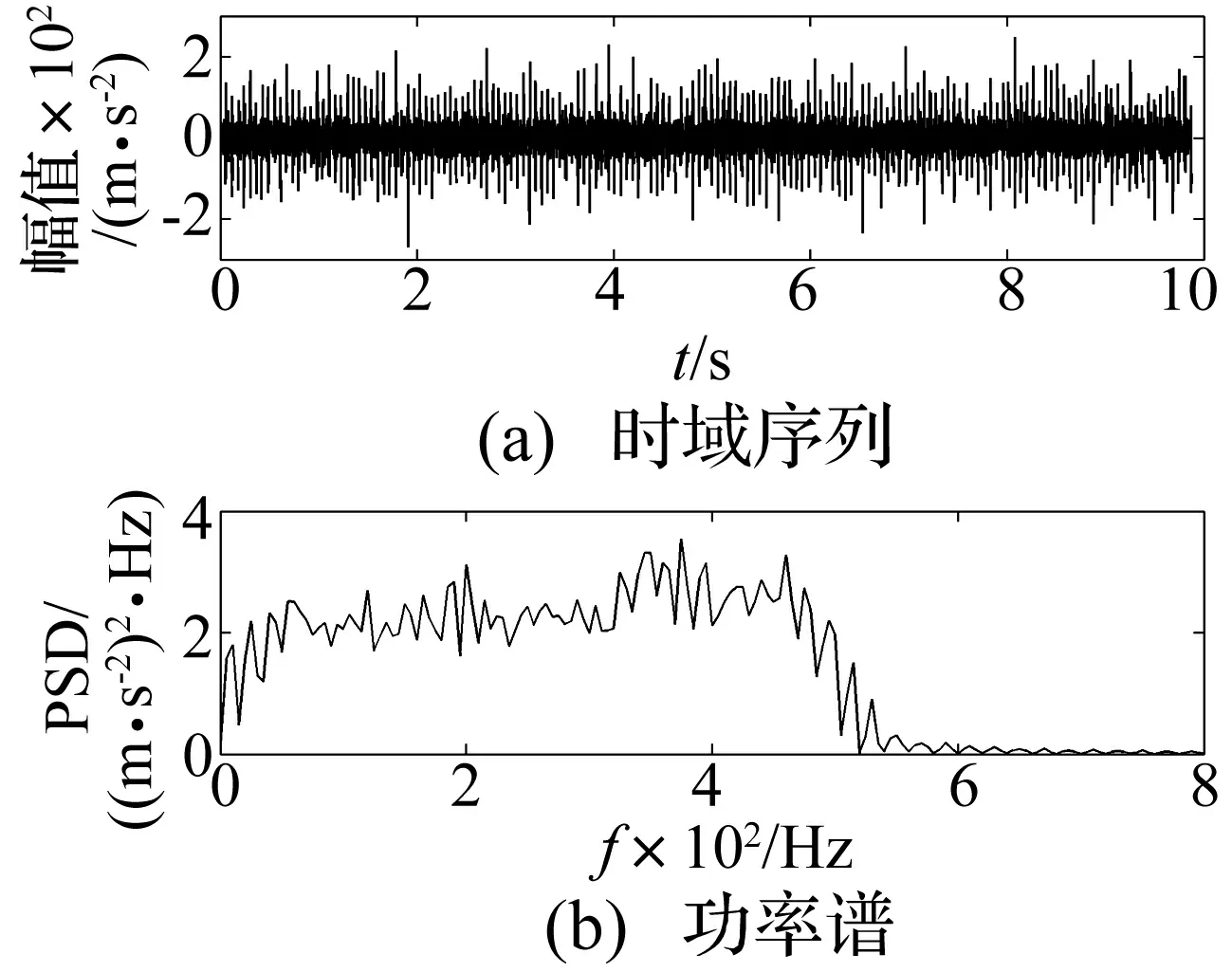
圖1 仿真非高斯振動信號，峭度：8.1394

將圖1(a)所示的樣本序列代入式(8)，得，

(14)

將上式代入方程組(13)得，

(15)

將式(15)代入式(7)，得非高斯幅值概率密度函數，

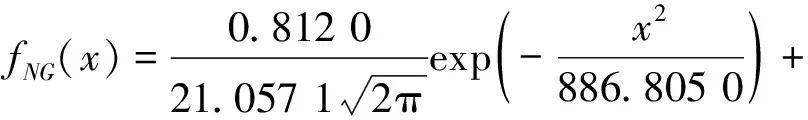
(16)

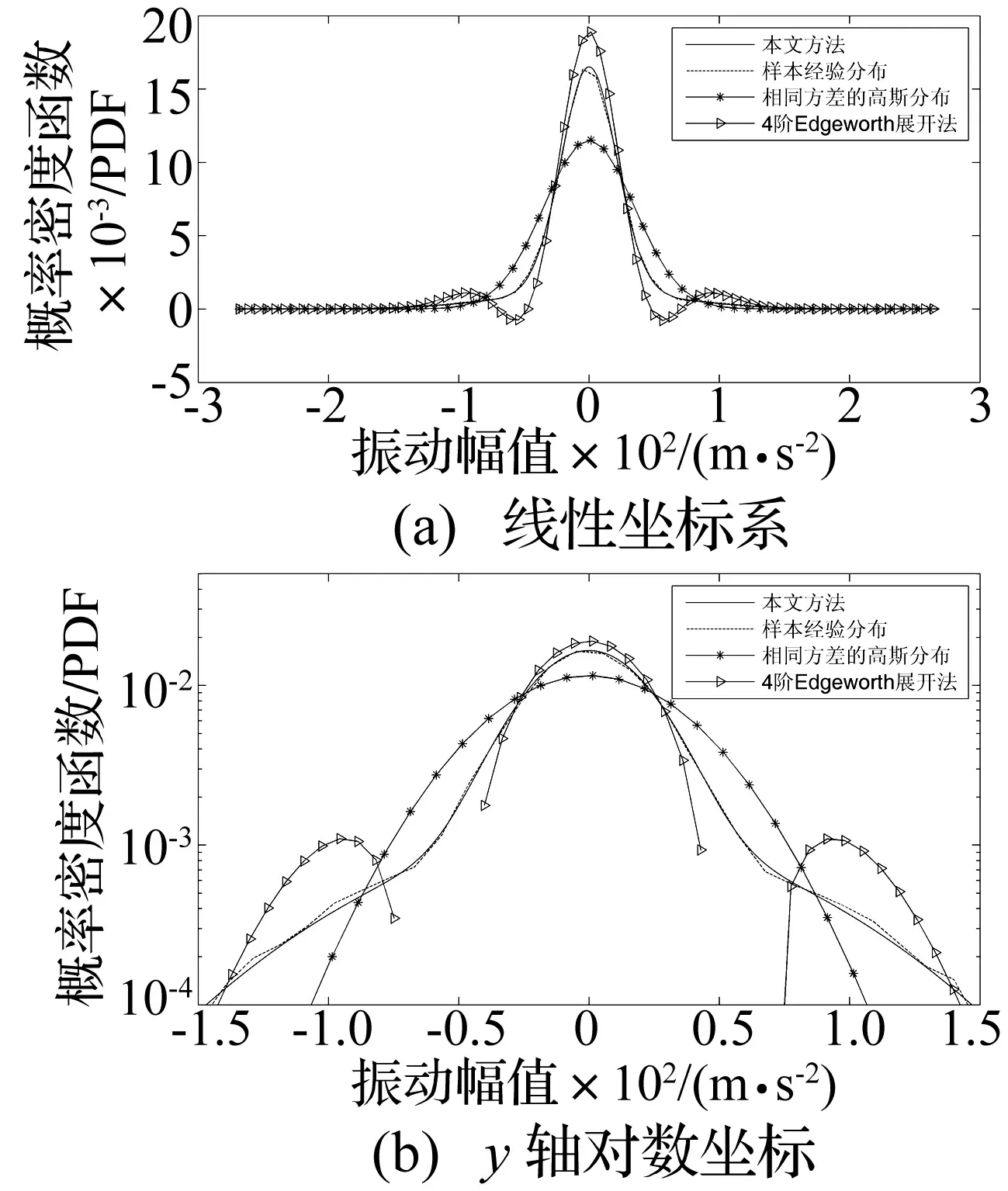
圖2 仿真非高斯信號幅值概率密度曲線

圖2給出了基于以下四種方法得到的概率密度曲線：① 樣本序列的經驗分布；② 本文所提出的高斯混合模型；③ 高斯假設分布；④ 四階Edgeworth展開法。因為時域樣本序列有足夠的長度，所以認為經驗分布有足夠高的精度，以它作為其他數學模型的參考標準。圖2(a)為線性坐標下的概率密度曲線，可以清晰地顯示出分布曲線中間峰值部分的差異；圖2(b)為半對數坐標下的幅值概率密度曲線，可以清晰地顯示出分布曲線在尾部的差異。從圖2可以看出，基于高斯假設的概率密度曲線與經驗分布曲線差異很大，所以工程中基于高斯假設來處理非高斯信號將引入很大的誤差；基于4階Edgeworth展開的非高斯幅值概率密度曲線出現了負值和多峰態，Edgeworth展開法只適用于峭度值很小的非高斯振動信號；基于本文提出的高斯混合法無論是在分布曲線的尖峰附近還是尾部都能精確地逼近經驗分布。

3.2 實測信號

某型運輸車輛載貨平臺實測振動信號，如圖3所示。該振動信號的均值為0，方差為38.646 2，偏斜度為0，峭度為22.971 6。圖3(a)為信號的時域序列；圖3(b)為功率譜密度，該振動信號具有窄帶非高斯特性。

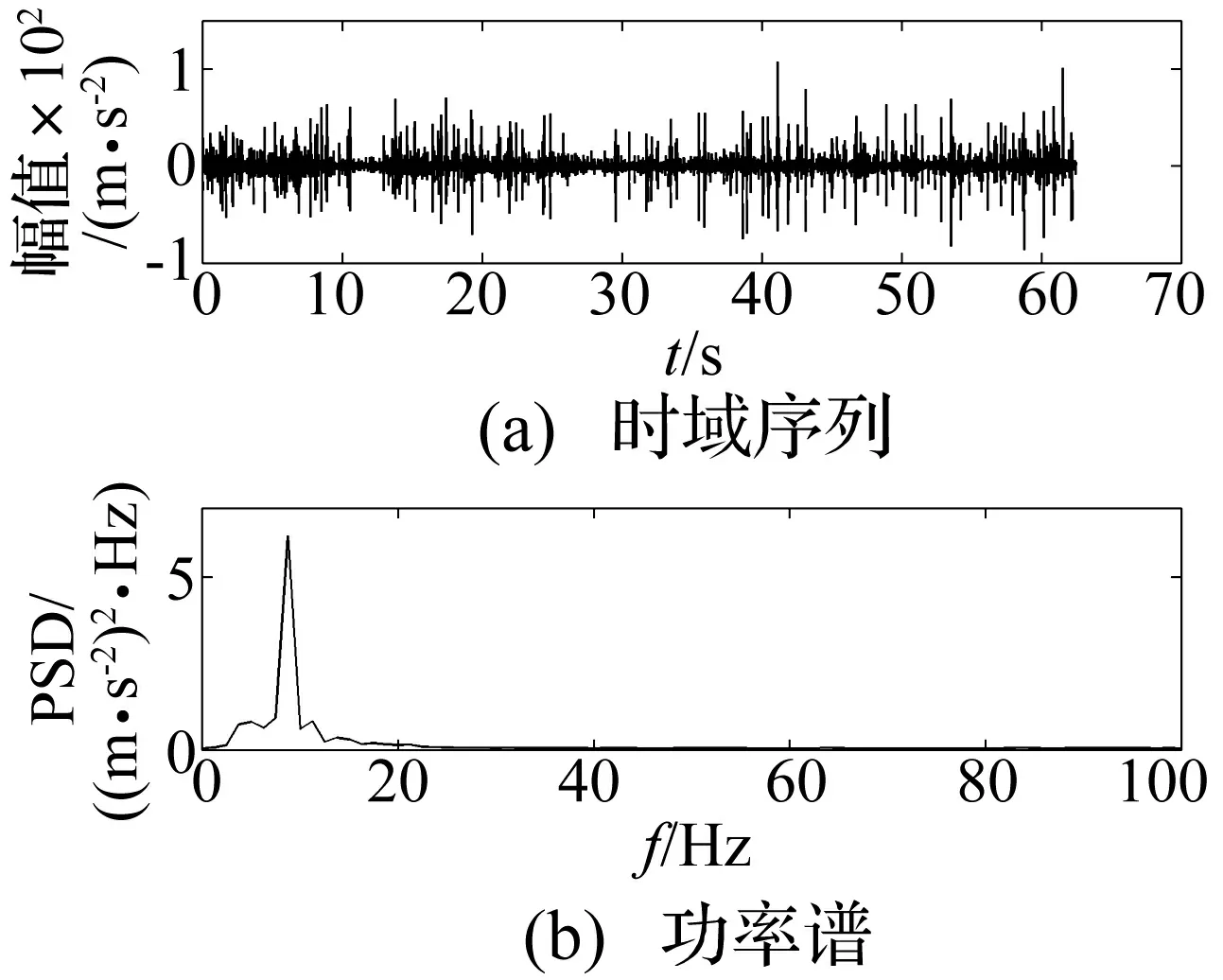
圖3 車輛測量非高斯振動信號，峭度為22.9716

將圖3(a)中的樣本序列代入式(8)得，

(17)

將式(17)代入方程組(13)得，

(18)

將式(18)代入(7)，得非高斯幅值概率密度函數，

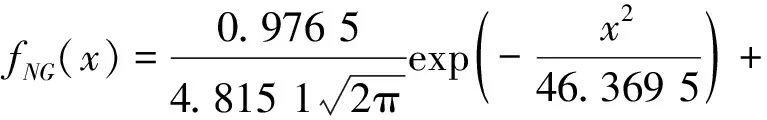
(19)

圖4給出了3.1所述的四種方法的概率密度曲線。同樣采用樣本經驗分布作為其他數學模型的參考標準。可以看出，隨著峭度的增加，基于高斯假設和Edgeworth展開的概率密度函數的誤差將會增大，而本文所提出的方法仍能夠較好地逼近樣本信號的經驗分布。

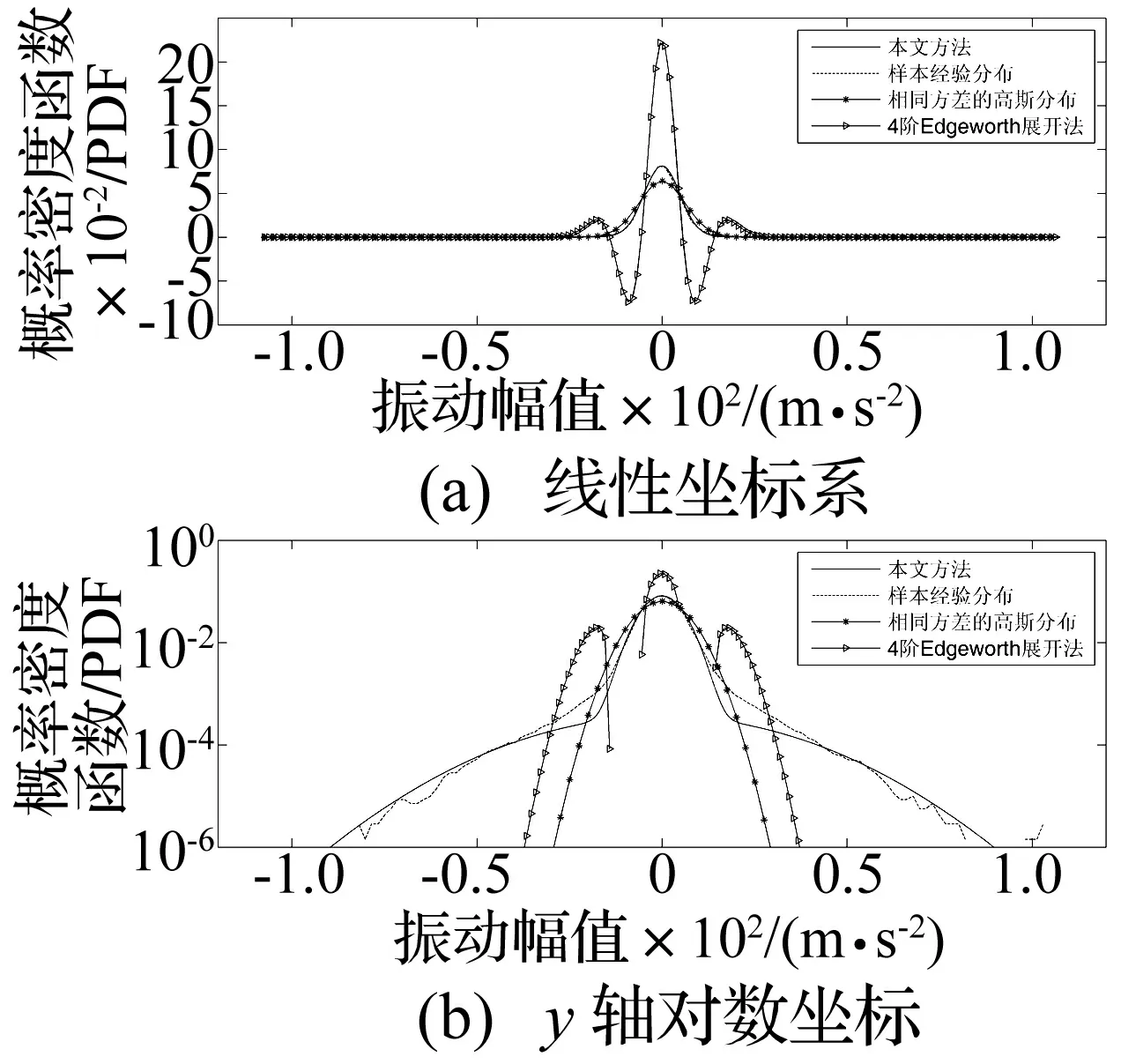
圖4 車輛非高斯信號的幅值概率密度曲線

3.3 結果分析

為了進一步分析所提出方法的準確性，這里以相對均方誤差來衡量各幅值概率密度曲線對經驗分布曲線的偏離程度。這里定義相對均方誤差為，

(20)

其中f為基于某種模型或方法得到的非高斯概率密度函數，fEM為基于樣本序列得到的經驗分布。

為了充分驗證方法的有效性，在3.1和3.2兩個示例的基礎上，又分別引入了一個峭度較低的仿真信號和某型飛機實測非高斯振動信號。分別計算了本文提出的高斯混合模型概率密度函數、高斯假設下的概率密度函數和基于Edgeworth展開的概率密度函數與樣本經驗分布之間的相對均方誤差，如表1所示。

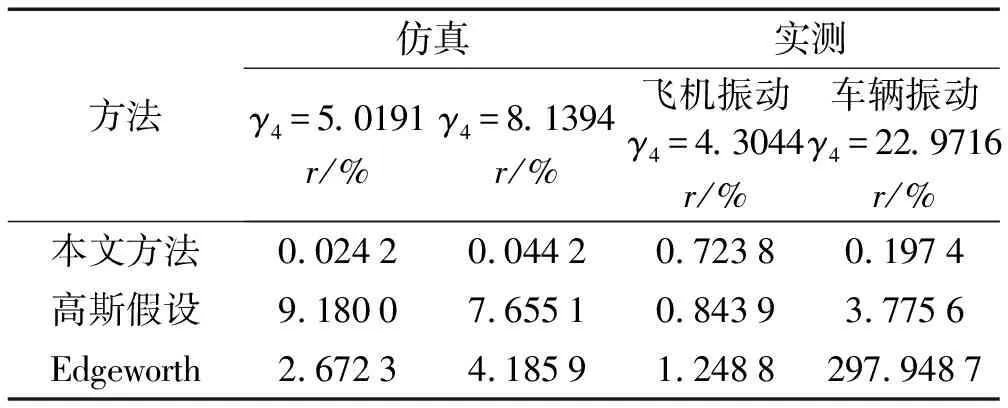
表1 非高斯振動幅值概率密度函數相對誤差r

4 結 論

基于高斯混合模型，利用高斯隨機變量高階矩之間的定量關系，結合非高斯隨機振動信號的物理特性，提出了一種求解非高斯振動幅值概率密度函數的方法，即二階高斯混合模型分解方法。該方法的數學模型簡單，物理意義明確，對高峭度的非高斯振動信號仍然適用。

通過仿真和實測非高斯振動信號驗證了方法的有效性和工程適用性。基于高斯混合模型的概率密度函數模型為非高斯機械振動信號的進一步研究，如疲勞分析，減振隔振等，提供了準確的統計分析工具和重要的理論支撐。

另外，二階高斯混合模型為非高斯振動的研究提供了重要思路，它可以進一步擴展為高階模型或應用于非高斯振動信號的頻域研究，以滿足更高精度和更深層次的研究需求。

參 考 文 獻

[1]Steinwolf A, Rizzi S A. Non-Gaussian analysis of turbulent boundary layer fluctuating pressure on aircraft skin panels [J]. Journal of Aircraft, 2006, 43 (6): 1662-1675.

[2]Gioffré M, Gusella V, Grigoriu M. Simulation of non-Gaussian field applied to wind pressure fluctuations [J]. Probabilistic Engineering Mechanics, 2000, 5(4): 339-346.

[3]Gurley K R, Kareem A, Tognarelli M A. Simulation of a class of non-normal random processes [J]. International Journal of Non-linear Mechanics, 1996, 31 (5): 601-617.

[4]董 欣, 葉繼紅. 馬鞍屋蓋表面面積平均風壓特性研究[J]. 振動與沖擊, 2011, 30 (7): 21-30.

DONG Xin, YE Ji-hong. Area-averaged wind pressure on a saddle roof [J]. Journal of Vibration and Shock, 2011, 30 (7): 21-30.

[5]Rouillard V. On the non-Gaussian nature of random vehicle vibrations [C]// WCE 2007. Proceedings of the World Congress on Engineering 2007. London, U K: WCE, 2007: 1219-1224.

[6]Rychlik I, Johannesson P, Leadbetter M R. Modeling and statistical analysis of ocean-wave data using transformed Gaussian processes [J]. Marine Structures, 1997, 10(1): 13-47.

[7]Podgórski K, Rychlik I, Machado U B. Exact distributions for apparent waves in irregular seas [J]. Ocean Engineering, 2000, 27(9): 979-1016.

[8]Butler R W, Machado U B, Rychlik I. Distribution of wave crests in a non-Gaussian sea [J]. Applied Ocean Research, 2009, 31(1): 57-64.

[9]Harremo?s P. Maximum entropy and the Edgeworth expansion [C]// IEEE. Proceedings of the IEEE Information theory workshop. Awaji Island, Japan: IEEE, 2005: 68-71.

[10]Winterstein S R. Nonlinear vibration models for extremes and fatigue [J]. Journal of Engineering Mechanics, 1988 114 (10): 1772-1790.

[11]Steinwolf A. Approximation and simulation of probability distributions with a variable kurtosis value [J]Computational Statistics & Data Analysis, 1996, 21 (2): 163-180.

[12]Rouillard V. The synthesis of road vehicle vibrations based on the statistical distribution of segment lengths, 5th Australasian Congress on Applied Mechanics, ACAM 2007 10-12 December 2007, Brisbane, Australia

[13]Mendel J M. Tutorial on higher-order statistics (spectra) in signal processing and system theory: theoretical results and some applications [J]. Proceedings of the IEEE, 1991, 79 (3): 278-305.

[14]Swami A, Mendel J M, Nikias C L. Higher-order spectral analysis toolbox for use with Matlab, user's guide, version 2 [EB/OL].http://www.uic.edu/classes/idsc/ids594/research/BBC/hosa.pdf. 2000.12.27/2012.12.20.

[15]Benasciutti D, Tovo R. Fatigue life assessment in non-Gaussian random loadings [J]. International Journal of Fatigue, 2006, 28 (7):733-746.

[16]蔣 瑜, 陳 循, 陶俊勇,等. 指定功率譜密度、偏斜度和峭度值下的非高斯隨機過程數字模擬[J]. 系統仿真學報, 2006, 18 (5): 1127-1130.

JIANG Yu, CHEN Xun, TAO Jun-yong, et al. Numerically simulating non-Gaussian random processes with specified PSD, skewness and kurtosis [J]. Journal of System Simulation, 2006, 18 (5): 1127-1130.

[17]蔣 瑜, 陶俊勇, 王得志,等. 一種新的非高斯隨機振動數值模擬方法[J]. 振動與沖擊, 2012, 31 (19): 169-173.

JIANG Yu, TAO Jun-yong, WANG De-zhi et al. A novel approach for numerical simulation of a non-Gaussian random vibration [J]. Journal of Vibration and Shock, 2012, 31 (19): 169-173.

[18]Rizzi S A, Przekop A, Turner T. On the response of a nonlinear structure to high kurtosis non-Gaussian random loadings [EB/OL]. http://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/ 20110013658_2011014239.pdf. 2011.7.4/ 2012.12.26.

[19]Middleton D. Non-Gaussian noise models in signal processing for telecommunications: new methods and results for class A and class B noise models [J]. IEEE Transactions on Information Theory, 1999, 45(4): 1129-1149.

[20]Vastola K. Threshold detection in narrow-band non-Gaussian noise [J]. IEEE Transactions on Communications, 1984, 32 (2): 134-139.

[21]Bendat J S, Piersol A G. 隨機數據分析方法 [M]. 凌福根. 北京: 國防工業出版社, 1980.