一類二維重構形的通有基底

高瑞梅,裴東河

(1. 長春理工大學 理學院,長春 130022； 2. 東北師范大學 數學與統計學院,長春 130024)

一類二維重構形的通有基底

高瑞梅1,裴東河2

(1. 長春理工大學 理學院,長春 130022； 2. 東北師范大學 數學與統計學院,長春 130024)

給出了重構形所形成集合通有基底的概念及(1,2)-型二維重構形的定義,并構造了它們的通有基底.

超平面構形； 重構形； 自由性； 通有基底

超平面構形是一類具有非孤立奇點的超曲面,它與組合學、 代數學、 拓撲學和代數幾何學中的多個學科廣泛交叉[1]. 超平面構形是有限維向量空間中有限個超平面所形成的集合,超平面構形通常簡稱為構形. 目前,構形的研究主要集中于構形的自由性問題及復空間中構形余集的拓撲性質等問題[2-6]. Yoshinaga[3]利用重構形的自由性解決了Edelman-Reiner猜想， 但自由重構形導子模的基底不易求出,且指數的變化不規律. 即使對于二維的重構形,其指數的描述都非常困難[7]. 因此,基底的構造更難. 文獻[8]對含有3個超平面、 重數取任意值的一類二維重構形給出了基底. 本文主要考慮(1,2)-型二維重構形(A,m),即重數m為1或2的一類重構形,構造出它們的通有基底.

1 基本概念

設V是一個n維向量空間,V中(n-1)維仿射子空間稱為V的一個超平面,記為H.V中有限個超平面組成的集合稱為一個超平面構形,記為A. 如果構形A中的每個超平面H都經過原點,則稱A是一個中心構形. 定義構形A的維數dimA=dimV=n. 用S表示由V*的基底x1,x2,…,xn生成的多項式代數. 對于A中的超平面H,可以選取αH∈S,使得H=Ker(αH). 對于中心構形A,定義導子模D(A)={θ|θ(αH)∈αHS,?H∈A}. 若D(A)是S上的一個自由模,則稱構形A是自由的.

設A是一個中心構形,映射m:A→稱為構形A的重數. 把(A,m)定義為一個重構形,顯然,重構形是構形的一個自然推廣. 類似于超平面構形,定義重構形的導子模

D(A,m)={φ|φ(αH)∈(αH)m(H)S,?H∈A}.

若D(A,m)是S上的一個自由模,則稱重構形(A,m)是自由的.

2 (1,2)-型二維重構形的通有基底

定義1設F是由若干n維重構形組成的集合,如果存在n個導子θ1,θ2,…,θn,使得對任意的重構形(A,m)∈F,θ1,θ2,…,θn均為D(A,m)的基底,則稱θ1,θ2,…,θn是集合F的通有基底.

若F只包含一個自由重構形,則此重構形的基底即為F的通有基底. 由于二維重構形都是自由的,因此本文在二維重構形范圍內考慮通有基底的存在性及其構造形式.

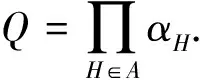
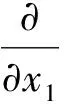
例2[9]設A是一個中心構形,Q為構形A的定義多項式,定義

則{θ1,θ2}構成了集合F2={(A,m)|m=2}的通有基底.

對目前產業環境和前景表示樂觀的MTC主席拿督Low Kian Chuan，在對國際木文化學會記者的采訪中說道，他真切地希望馬來西亞木材產業生產商能進一步解放思想，開拓視野，提高產品質量，加快技術升級。

定義2設A和B是兩個中心構形,且A∩B=?. 定義m:A∪B→如下：

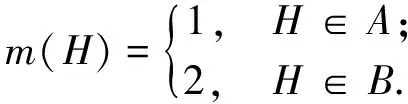
則構形(A∪B,m)稱為(1,2)-型重構形.

引理1[10]如果θ1,θ2,…,θn∈D(A,m),則它們形成D(A,m)的一組基底當且僅當

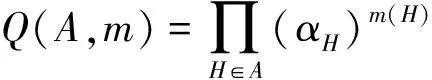
定理1設構形(A∪B,m)是一個(1,2)-型重構形,QA,QB分別為A和B的定義多項式,則集合F={(A∪B,m)|m(A)=1,m(B)=2}的通有基底存在,形式如下：

證明： 由引理1,先計算如下行列式：

1) 如果H∈A,則αH|QA,因此

即θ1(αH)=-αH(D1(QA)D2(QB)-D2(QA)D1(QB))-QB(aD2(QA)-bD1(QA))∈αHS.

2) 如果H∈B,則αH|QB,因此

綜合1),2)可知,θ1∈D(A∪B,m).

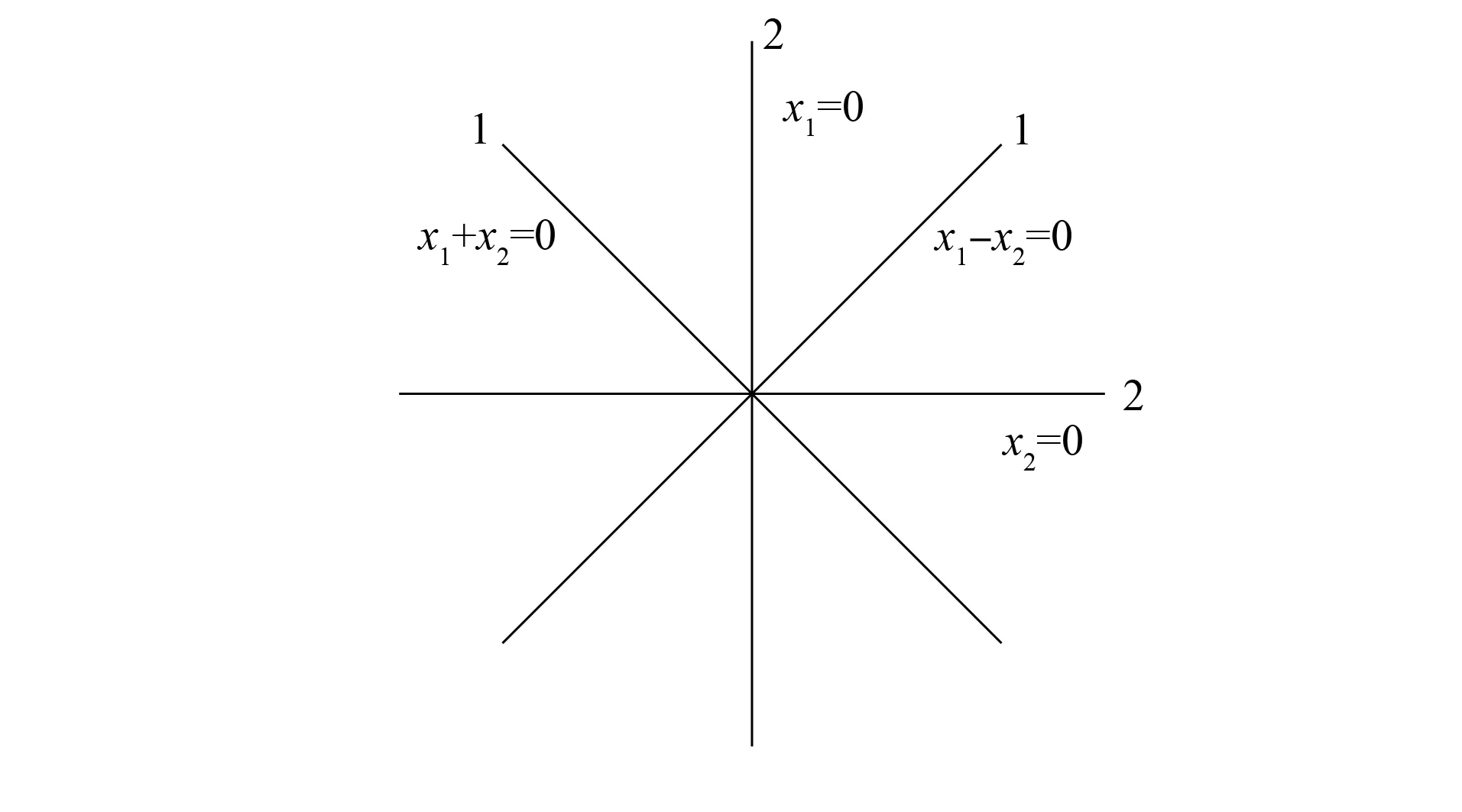
圖1 含有6個超平面的(1,2)-型重構形Fig.1 (1,2)-Type multiarrangement with six hyperplanes

此外,由于θ2(αH)=αHQB,因此對于H∈A,有αH|θ2(αH)； 對于H∈B,有(αH)2|θ2(αH),即θ2∈D(A∪B,m). 由引理1可知,θ1,θ2構成了(A∪B,m)的一組基底. 證畢.

下面利用定理1給出一個(1,2)-型重構形基底.

例3設(A,m)是一個重構形,其中

幾何結構如圖1所示. 由定理1,

形成了D(A,m)的一組基底.

[1]Orlik P,Terao H. Arrangements of Hyperplanes [M]. Berlin: Springer-Verlag,1992.

[2]Terao H. Generalized Exponents of a Free Arrangement of Hyperplanes and Shephard-Todd-Brieskorn Formula [J]. Inventiones Mathematicae,1981,63: 159-179.

[3]Yoshinaga M. Characterization of a Free Arrangement and Conjecture of Edelman and Reiner [J]. Inventiones Mathematicae,2004,157(2): 449-454.

[4]GAO Ruimei,PEI Donghe,Terao H. The Shi Arrangement of the TypeDl[J]. Japan Academy Proceedings. Series A: Mathematical Sciences,2012,88(3): 41-45.

[5]Suyama D,Terao H. The Shi Arrangements and the Bernoulli Polynomials [J]. The Bulletin of the London Mathematical Society,2012,44(3): 563-570.

[6]Yuzvinsky S A. Orlik-Solomon Algebras in Algebra and Topology [J]. Russian Mathematical Surveys,2001,56(2): 293-364.

[7]Wakefield M,Yuzvinsky S. Derivations of an Effective Divisor on the Complex Projective Line [J]. Transactions of the American Mathematical Society,2007,359(9): 4389-4404.

[8]Wakamiko A. On the Exponents of 2-Multiarrangements [J]. Tokyo Journal of Mathematics,2007,30(1): 99-116.

[9]Solomon L,Terao H. The Double Coxeter Arrangement [J]. Commentarii Mathematici Helvetici,1998,73(2): 237-258.

[10]Ziegler G M. Multiarrangements of Hyperplanes and Their Freeness [J]. Contemporary Mathematics,1989,90: 345-359.

(責任編輯： 趙立芹)

UniversalBasesforaClassofTwo-DimensionalMultiarrangements

GAO Ruimei1,PEI Donghe2
(1.CollegeofScience,ChangchunUniversityofScienceandTechnology,Changchun130022,China;
2.SchoolofMathematicsandStatistics,NortheastNormalUniversity,Changchun130024,China)

For a set of multiarrangements,we gave the concept of universal basis,offered the definition of (1,2)-type multiarrangement of two-dimensional,and also constructed the universal bases for all of them.

hyperplane arrangement; multiarrangement; freeness; universal basis

2013-09-05.

高瑞梅(1983—),女,漢族,博士,講師,從事奇點理論和超平面構形的研究,E-mail: gaorm135@nenu.edu.cn.

國家自然科學基金(批準號： 11326078)和黑龍江省教育廳科技研究項目(批準號： 12531187).

O189

A

1671-5489(2014)05-0979-03