一維波在水下多層介質(zhì)中傳播的時(shí)域解析解
金澤宇, 殷彩玉, 諶 勇, 黃修長(zhǎng), 華宏星
(上海交通大學(xué) 振動(dòng)、沖擊、噪聲研究所,上海 200240;上海交通大學(xué) 機(jī)械系統(tǒng)與振動(dòng)國(guó)家重點(diǎn)實(shí)驗(yàn)室,上海 200240)
隨著現(xiàn)代武器的發(fā)展和對(duì)艦艇生命力要求的提高,對(duì)艦艇低輻射噪聲和高抗爆炸沖擊性能的研究越來(lái)越受到各國(guó)海軍的重視。目前通常在艦艇的艇體表面敷設(shè)一層多孔介質(zhì)覆蓋層以達(dá)到抗沖隔聲的目的。因此研究在水下爆炸沖擊波輸入情況下,表面敷設(shè)覆蓋層后對(duì)艦艇艇體表面壓力波的影響顯得極為重要。
波在多層介質(zhì)傳播的問(wèn)題有過(guò)很多研究。書(shū)籍[1-2]介紹了許多計(jì)算簡(jiǎn)諧問(wèn)題的公式,得到了解析和半解析的解。然而這些解不能解決考慮到全部復(fù)雜反射和透射情況的波在多層介質(zhì)中傳播的問(wèn)題。在本文中邊值問(wèn)題是主要考慮的對(duì)象,這個(gè)問(wèn)題的解通常采用頻域方法或者時(shí)域方法。在頻域(傅里葉對(duì)時(shí)間做變換)方法中,波有限元法(WFE method)[3-7]是很好的選擇,雖然這些方法會(huì)產(chǎn)生數(shù)值困難,但可以通過(guò)使用一些代數(shù)技巧避免。
本文的重點(diǎn)是時(shí)域方法,它主要包含了兩種方法,一種是數(shù)值方法,一種是解析方法。前人做過(guò)了許多工作,例如有限時(shí)域差分法[8-11],有限元法(FEM)[12-15]。Desceliers等[16]發(fā)展了一種新的數(shù)值雜交方法來(lái)仿真在給定瞬態(tài)載荷的情況下瞬態(tài)波在有多層的可以是液體或者固體的半無(wú)限介質(zhì)中傳播的問(wèn)題。對(duì)于有限元法,Brasek[17-18]得到了一維有覆蓋層的鋁結(jié)構(gòu)在階躍載荷下的瞬態(tài)響應(yīng),并且研究了在指數(shù)波輸入情況下的金屬結(jié)構(gòu)的響應(yīng)特性。他的研究顯示不管覆蓋層的類型和邊界介質(zhì)如何,結(jié)構(gòu)的應(yīng)力和節(jié)點(diǎn)速度隨著覆蓋層剛度的下降而上升。Neilson等[19]運(yùn)用有限元和雙漸進(jìn)逼近法(DAA)得到了在平面階躍壓力下沉浸雙層彈性球殼的瞬態(tài)響應(yīng),兩層殼之間充滿流體。Bergersen[20]得到了在水下爆炸沖擊波下的貼有橡膠材料的金屬圓柱的動(dòng)態(tài)響應(yīng)。他的研究發(fā)現(xiàn)在一定的幾何條件和覆蓋層材料特性條件下,貼覆蓋層在動(dòng)態(tài)響應(yīng)方面有負(fù)面的影響。雖然在理論上時(shí)域數(shù)值方法能解決復(fù)雜的問(wèn)題,但是一些缺點(diǎn)仍然存在。一是數(shù)值方法本身不精確,更重要的是我們可能不會(huì)完全理解問(wèn)題的機(jī)理,而且在對(duì)參數(shù)分析時(shí),需要大量的工作。
對(duì)于解析解,雖然它們不能獲得所有問(wèn)題特別是復(fù)雜問(wèn)題的精確解,但是它們對(duì)于相對(duì)簡(jiǎn)單的問(wèn)題的結(jié)果能夠幫助人們透徹地理解機(jī)理。此外,還能夠?yàn)閺?fù)雜問(wèn)題提供指導(dǎo)。在過(guò)去的研究中,一些人做了解析方面的工作。Taylor[21]研究了弱沖擊與氣背板的作用,得到了一維解析解。Snay等[22]運(yùn)用特征線法考慮了強(qiáng)沖擊和氣背板作用,改進(jìn)了Taylor的結(jié)果。Schechter等[23]考慮的與弱沖擊作用的板可以是氣背或者水背的。Huang[24]運(yùn)用Laplace和Hankel變換研究了在球面沖擊波作用下的大彈性平板的初始瞬態(tài)響應(yīng)。童宗鵬[25]采用波動(dòng)理論,拓展Taylor平板模型,研究了水下爆炸沖擊波在水、覆蓋層、空氣層、船體鋼中的傳播過(guò)程,建立了實(shí)心覆蓋層結(jié)構(gòu)和含空腔覆蓋層結(jié)構(gòu)的流固耦合模型,但其只考慮了一次反射波。諶勇等[26]運(yùn)用多自由度系統(tǒng)模擬艦船覆蓋層的動(dòng)態(tài)模型。然而這些解存在一些假設(shè),并且沒(méi)有給出考慮多重反射透射的解析解。
本文的目的是基于波動(dòng)理論提出一種解決一維波在多層介質(zhì)中傳播的時(shí)域解析解。這種新方法通過(guò)考慮在多層介質(zhì)中任意輸入下的多次反射透射獲得準(zhǔn)確的瞬態(tài)解。通過(guò)無(wú)量綱參數(shù)分析獲得峰值壓力隨覆蓋層阻抗、厚度和指數(shù)波衰減常數(shù)的變化。
1 時(shí)域解析解
水中壓力波經(jīng)覆蓋層-鋼板后,會(huì)產(chǎn)生一系列的反射和透射現(xiàn)象,隨著反射和透射次數(shù)的增多,情況越來(lái)越復(fù)雜。本文所提出的方法不考慮壓力波在覆蓋層-鋼板中反射透射的具體傳播方式,而是從某一特定時(shí)刻出發(fā),分析在該時(shí)刻壓力波在覆蓋層和鋼板中可能的傳播方式,將這些傳播方式組合即可得到壓力波在多層介質(zhì)中的響應(yīng)。具體的思路如下:對(duì)于某一特定時(shí)刻tm,n,從覆蓋層透射到水中的壓力增量記為f(tm,n,t),該透射波在覆蓋層中傳播m次,在鋼板中傳播n次。對(duì)這一特定時(shí)刻,m和n是定值,但從整體的時(shí)間上看,m可以取1→∞,n可以取0→∞,m和n的任意組合都有可能,對(duì)于這一特定時(shí)刻,就是所有組合中的一種。基于上述想法,若波在覆蓋層以及在鋼板中傳播一次的時(shí)間已知,則可計(jì)算出所有m和n的組合所對(duì)應(yīng)的時(shí)刻,對(duì)這些時(shí)刻從小到大排序,就得到每次從覆蓋層中透射到水中的壓力波的情況,獲得波在多層介質(zhì)中傳播的時(shí)域解析解。
1.1 基本假設(shè)
在壓力波波幅不大的情況下,將水、覆蓋層、鋼板簡(jiǎn)化為一維問(wèn)題,并做以下假設(shè):
(1) 假設(shè)應(yīng)力波在各介質(zhì)中的傳播形式為縱波;
(2) 假設(shè)各個(gè)介質(zhì)為均勻介質(zhì),有固定線性阻抗;
(3) 忽略波傳播過(guò)程中阻尼的影響;
(4) 忽略覆蓋層、鋼板的剛體運(yùn)動(dòng);
(5) 忽略波傳播引起的介質(zhì)變形對(duì)波在每層介質(zhì)中傳播時(shí)間的影響。
1.2 系統(tǒng)簡(jiǎn)化模型及模型參數(shù)
對(duì)于有水、覆蓋層和鋼板三層介質(zhì)的系統(tǒng),簡(jiǎn)化后的模型為:介質(zhì)1是水,且左邊是無(wú)限的;中間介質(zhì)2是有限厚度的覆蓋層;右側(cè)介質(zhì)3是鋼板,鋼板右側(cè)邊界Ⅲ可以是不同的邊界條件,如氣背、水背、剛性邊界等。系統(tǒng)簡(jiǎn)化模型圖如圖1所示。
簡(jiǎn)化后的系統(tǒng)的物理參數(shù)如下:密度:ρ1,ρ2,ρ3;波速:c1,c2,c3;阻抗率:R1,R2,R3;介質(zhì)厚度:h2,h3。
波在不同介質(zhì)中傳播參數(shù)如下:反射系數(shù)與透射系數(shù):r12,s12,r21,s21,r23,s23,r32,s32,rⅢ(其中rab為波由介質(zhì)a到介質(zhì)b的反射系數(shù),sab為波由介質(zhì)a到介質(zhì)b的透射系數(shù),rⅢ為邊界Ⅲ的反射系數(shù))。
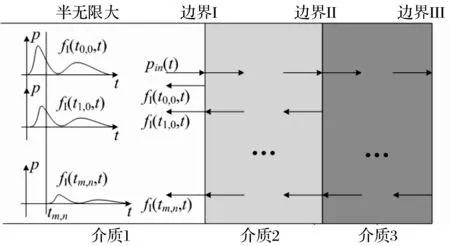
圖1 系統(tǒng)簡(jiǎn)化模型
1.3 時(shí)域解析解
根據(jù)聲學(xué)理論知,均勻理想彈性媒質(zhì)中一維小振幅線性聲波方程為:
(1)
由之前的假設(shè)可知,本文考慮的波滿足此方程。在邊界Ⅱ處反射波返回到邊界Ⅰ之前,介質(zhì)1中存在行波解:
(2)
介質(zhì)2中的透射波:
(3)
粒子振動(dòng)速度滿足歐拉方程:
(4)
可得:
(5)
由此可知:對(duì)于任意F、G,壓力p與粒子振動(dòng)速度v的關(guān)系與簡(jiǎn)諧入射波是等同的。所以輸入可取簡(jiǎn)諧波、指數(shù)衰減波、三角波等任意波。
(1) 特定時(shí)刻濕表面壓力增量
設(shè)壓力波在介質(zhì)2和介質(zhì)3傳播一次的時(shí)間分別為:
(6)
對(duì)于某一特定時(shí)刻,有一壓力波從覆蓋層透射到水中,該壓力波在覆蓋層中傳播m次,在鋼板中傳播n次,則對(duì)應(yīng)的時(shí)刻tm,n為:
tm,n=m×ts2+n×ts3
(7)
設(shè)在特定時(shí)刻tm,n由介質(zhì)2透射到介質(zhì)1中的壓力波增量為f(tm,n,t),pin(t)為初始時(shí)刻入射波,f(t0,0,t)為初始時(shí)刻的反射波。其中初始時(shí)刻反射波可以表示為:
f(t0,0,t)=r12·pin(t)
(8)
在初始時(shí)刻以后的時(shí)間里(即m≥1),當(dāng)n=0時(shí),波沒(méi)有透射到介質(zhì)3中,此時(shí)從介質(zhì)2透射到介質(zhì)1中的波記為f(tm,0,t):
f(tm,0,t)=s12s21(r21r23)m-1r23·pin(t-tm,0)
(9)
其過(guò)程可以簡(jiǎn)述為入射波透射進(jìn)入介質(zhì)2,在介質(zhì)2中來(lái)回傳播m-1次,最終透射回到介質(zhì)1中。
當(dāng)n≠0時(shí),此時(shí)波從介質(zhì)2透射到介質(zhì)3的次數(shù)從1→k都有可能。
波從介質(zhì)2到介質(zhì)3透射1次
f1(tm,n,t)=
pin(t-tm,n)
(10)
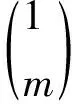
波從介質(zhì)2到介質(zhì)3透射2次
f2(tm,n,t)=
pin(t-tm,n)
(11)
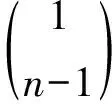
更一般地,波從介質(zhì)2到介質(zhì)3透射k次:
fk(tm,n,t)=
pin(t-tm,n)
(12)
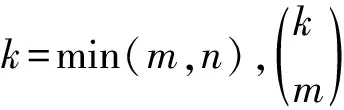
綜上所述:當(dāng)m≥1,n≠0時(shí),tm,n時(shí)刻由介質(zhì)2透射到介質(zhì)1的波為上述k種可能性的疊加,即:
(13)
當(dāng)m≥1,n=0時(shí),tm,n時(shí)刻由介質(zhì)2透射到介質(zhì)1的波由方程(9)給出結(jié)果,當(dāng)m=0,n=0,即初始時(shí)刻時(shí)的反射波由方程(8)給出結(jié)果。
(2) 每一時(shí)刻濕表面的壓力
(1)中介紹了對(duì)于特定時(shí)刻tm,n從介質(zhì)2透射到介質(zhì)1中的壓力波增量的計(jì)算方法,即m、n所有組合中的一種。現(xiàn)在算出m、n所有組合所對(duì)應(yīng)的時(shí)刻tm,n和該時(shí)刻從介質(zhì)2透射到介質(zhì)1的壓力增量f(tm,n,t)。先對(duì)tm,n進(jìn)行升序排列,根據(jù)tm,n的升序排列,將對(duì)應(yīng)該時(shí)刻的f(tm,n,t)重新排列,就得到順序的每一時(shí)刻從介質(zhì)2透射到介質(zhì)1的壓力增量。而對(duì)于每一時(shí)刻濕表面壓力,則為該時(shí)刻及以前所有順序的時(shí)刻從介質(zhì)2透射到介質(zhì)1的壓力增量的和。
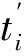
(14)
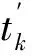
2 數(shù)值驗(yàn)證和算例
為了驗(yàn)證時(shí)域解析解的正確性,將圖1中各介質(zhì)材料參數(shù)賦值如表1所示。取入射波為指數(shù)衰減波p0exp(-t/θ),取衰減時(shí)間常數(shù)θ= 0.6 ms,壓力峰值p0為1 Pa。波在水、覆蓋層和鋼板中傳播,邊界Ⅲ可以是剛性邊界、氣背邊界和水背邊界。有限元模型由8節(jié)點(diǎn)的線性聲學(xué)的方形六面體單元構(gòu)成。在ABAQUS中的幾何模型如圖2所示,覆蓋層和鋼板包括740個(gè)線性聲學(xué)單元,水和空氣各包括50個(gè)單元,整個(gè)系統(tǒng)包括3 376個(gè)節(jié)點(diǎn)。
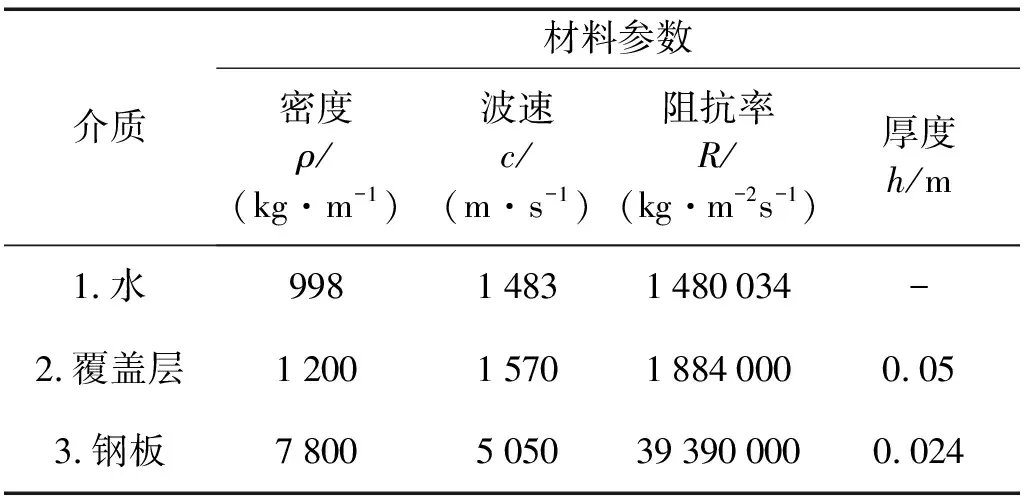
表1 三種介質(zhì)的材料參數(shù)
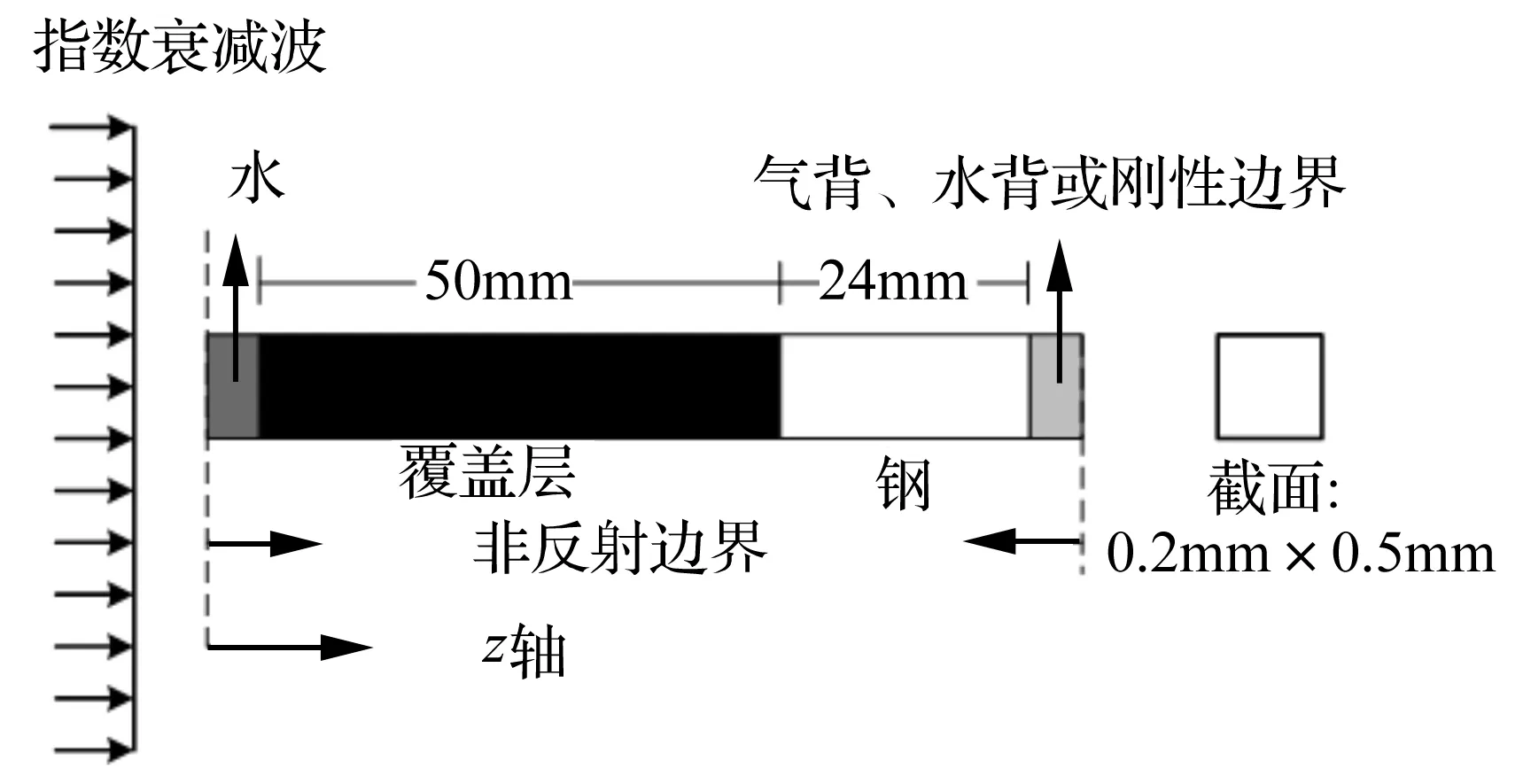
圖2 一維系統(tǒng)在ABAQUS中的模型
圖3、圖4和圖5分別為濕表面壓力時(shí)域解析解和有限元解在剛性邊界、氣背邊界和水背邊界下的對(duì)比。圖中有限元解開(kāi)始時(shí)有一個(gè)下降,而解析解沒(méi)有,是因?yàn)橛邢拊獠蓸娱g隔小,在開(kāi)始時(shí)采樣點(diǎn)比解析解多導(dǎo)致的。開(kāi)始時(shí)刻有限元解的下降是由于指數(shù)衰減波的衰減作用造成的,而不是有透射波到水中造成的。
從圖中可以看出解析解與有限元解吻合得很好,解析解每次突變的時(shí)間和壓力與有限元解對(duì)比都相差不大。不大的壓力差是由于有限元存在數(shù)值阻尼和誤差造成的。解析解與有限元解的對(duì)比可以說(shuō)明解析解的正確性。
圖6為指數(shù)衰減波對(duì)于不同邊界濕表面壓力的變化,從圖中可以看出:① 三種邊界下,濕表面總壓力最終都趨于0;② 衰減速度:氣背最快、水背次之、剛性邊界最慢;③ 氣背邊界時(shí),總壓力先衰減到負(fù)壓再趨于0。如果壓力充分大,氣背產(chǎn)生的負(fù)壓大于靜水壓,板將和水脫離。水背和剛性邊界從正壓直接衰減為0。
圖7為指數(shù)衰減波對(duì)于三種邊界濕表面振動(dòng)速度的變化,振動(dòng)速度可以由壓力通過(guò)方程(4)求得,從圖中可以看出剛性邊界振動(dòng)速度基本在0附近變化,而水背邊界、氣背邊界振動(dòng)速度則有較大變化。這是由于邊界Ⅲ的約束能力影響的,如果邊界Ⅲ自由,約束能力弱,振動(dòng)速度有較大變化。而水背、和剛性邊界對(duì)邊界Ⅲ約束能力強(qiáng),使得振動(dòng)速度不易有大變化。

圖3 剛性邊界濕表面壓力解析解與有限元解對(duì)比曲線
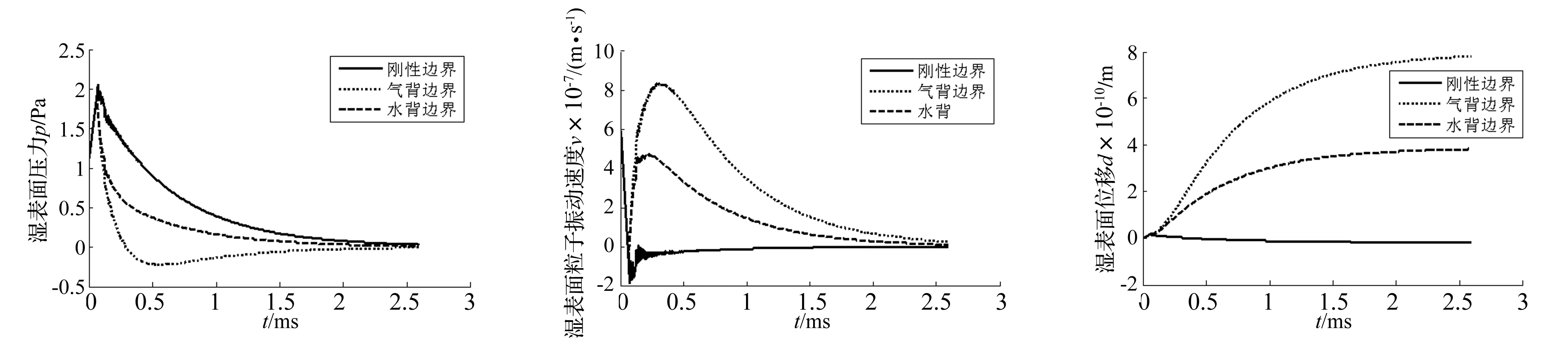
圖6 指數(shù)衰減波輸入對(duì)于三種邊界濕表面壓力曲線
圖8為指數(shù)衰減波濕表面位移的變化,位移曲線是由振動(dòng)速度曲線積分得到。從圖中可以看出:剛性邊界時(shí),濕表面位移為0;水背和氣背邊界時(shí),濕表面有剛體位移。因此,如果壓力波過(guò)大,則計(jì)算結(jié)果將不再準(zhǔn)確。
3 指數(shù)衰減波輸入的近似結(jié)果比較
上面提出的解析方法可考慮所有反射及透射的影響,得到的濕表面壓力的精確結(jié)果。下面針對(duì)邊界條件為剛性邊界、氣背邊界以及水背邊界時(shí),將精確結(jié)果與僅考慮前幾次反射透射的近似結(jié)果進(jìn)行比較。
圖9、圖10、圖11分別為剛性邊界、氣背邊界、水背邊界的近似結(jié)果與解析結(jié)果的對(duì)比圖。從這3個(gè)圖中可以看出:
(1) 僅考慮濕表面第一次反射波而不考慮在介質(zhì)2與3中波的情況,所得近似結(jié)果與實(shí)際結(jié)果相差很大;
(2) 僅考慮波在邊界Ⅱ上反射一次,不考慮波在介質(zhì)3中的傳播情況,對(duì)于剛性邊界近似結(jié)果與實(shí)際結(jié)果相差不大,但是近似結(jié)果無(wú)法反映壓力由于多次反射、透射所造成的震蕩效應(yīng);對(duì)于氣背邊界和水背邊界,結(jié)果則相差很大,考慮多次反射、透射的結(jié)果衰減的速度遠(yuǎn)大于僅考慮波在邊界Ⅱ上反射一次的結(jié)果。
所以僅考慮幾次反射、透射而認(rèn)為后續(xù)反射波、透射波很小可以忽略的近似方法存在缺陷。想得到準(zhǔn)確的結(jié)果,需要考慮足夠多的反射、透射波的作用。

圖9 剛性邊界下近似結(jié)果與解析結(jié)果比較
4 指數(shù)衰減波的無(wú)量綱化參數(shù)分析
對(duì)指數(shù)衰減波進(jìn)行無(wú)量綱化,設(shè)td2=ts2/θ,td3=ts3/θ,n1=R1/R2,n2=R2/R3,四個(gè)變量加上r3五個(gè)變量,構(gòu)成無(wú)量綱化后的5個(gè)參數(shù)。以下研究各個(gè)參數(shù)變化對(duì)結(jié)果的影響。
4.1 覆蓋層阻抗的影響
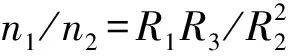
圖12為濕表面壓力峰值隨n1/n2比值變化曲線。從圖中可以看出:隨著覆蓋層阻抗減小(即n1/n2增大),各個(gè)邊界壓力波峰值先減小后增大再減小。當(dāng)n1/n2的比值近似為0.06時(shí),剛性邊界的峰值出現(xiàn)最小值;比值近似為0.5時(shí),氣背邊界、水背邊界的峰值出現(xiàn)最小值;當(dāng)n1/n2的比值近似為3時(shí),剛性邊界峰值出現(xiàn)最大值,超過(guò)了覆蓋層為剛性層時(shí)的峰值;比值近似為5時(shí),氣背邊界、水背邊界峰值出現(xiàn)最大值,但小于覆蓋層為剛性層時(shí)的峰值。當(dāng)n1/n2的比值繼續(xù)增大,三種邊界壓力波的峰值出現(xiàn)明顯減小。
峰值曲線先減小后增大再減小的原因可分析如下:① 對(duì)于剛性邊界,壓力的峰值主要是由第一次反射波、第二次透射波、第三次透射波(第三次透射是入射波進(jìn)入介質(zhì)2再進(jìn)入介質(zhì)3在邊界Ⅲ上反射后透射到介質(zhì)2再透射回介質(zhì)1的波)的疊加結(jié)果決定。在阻抗較大時(shí),起決定作用的是第一次反射波,隨著阻抗的減小,第一次反射波幅值減小,峰值曲線下降。阻抗繼續(xù)減小達(dá)到最低點(diǎn),此時(shí)起決定作用的是第二次和第三次透射波,隨著阻抗減小,第二次和第三次透射波幅值增強(qiáng),峰值曲線上升到最大值。隨著阻抗繼續(xù)減小,覆蓋層的特性趨于空氣,第一次透射波趨于0,后續(xù)作用越來(lái)越小,而第一次入射波和反射波之和也趨于0,所以最終結(jié)果使峰值越來(lái)越小;② 對(duì)于氣背邊界和水背邊界的情況,壓力峰值主要是由第一次反射波、第二次透射波的疊加結(jié)果決定,此處與剛性邊界不同,由于第三次透射波對(duì)于邊界Ⅲ剛性,壓力波變?yōu)樵瓉?lái)2倍,而若是氣背、水背邊界反射波相位相反,疊加將減小壓力波峰值,其余討論與剛性邊界相同。
4.2 覆蓋層厚度與衰減常數(shù)的影響
(1)改變td2、td3使之同比增大或減小
td2、td3同比增大或減小相當(dāng)于介質(zhì)2、3的厚度同比增加,或者波速同比減小,亦或θ減小。
圖13為同比例改變td2、td3,濕表面壓力峰值曲線,從圖中可以看出:隨著td2、td3同比例增大,壓力波峰值減小;衰減的速度越快。即同比增加介質(zhì)2、3的厚度或者減小輸入波的衰減常數(shù),可使?jié)癖砻嫔系目倝毫Ψ逯禍p小,衰減更快。
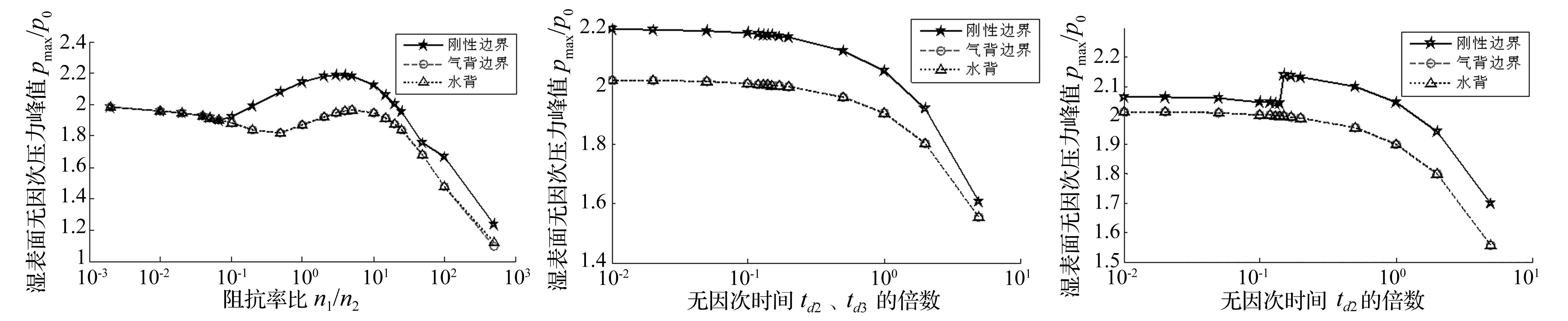
圖12 改變n1/n2濕表面無(wú)因次壓力峰值曲線
(2) 固定td3,改變td2
固定td3,改變td2中的參數(shù),使td2,td3具有不同的比例。這樣做相當(dāng)于改變覆蓋層厚度。
圖14為固定td3,改變td2中的參數(shù)濕表面壓力峰值的變化的曲線。從圖中可以看出對(duì)于剛性邊界隨著td2增大,壓力波峰值先減小再突變?cè)龃笤贉p小;對(duì)于氣背和水背邊界隨著td2增大時(shí),壓力波峰值減小。對(duì)于剛性邊界,壓力波峰值是由衰減作用和第三次透射作用共同決定的,曲線的前半段后后半段的下降趨勢(shì)是由于反射波與入射波疊加時(shí)的時(shí)間延長(zhǎng),入射波的衰減作用導(dǎo)致的。也可以理解為覆蓋層厚度變大,儲(chǔ)存能量的能力大了,等到釋放能量的時(shí)候,入射波已經(jīng)衰減很多了,導(dǎo)致疊加后的波峰減小,而峰值曲線的突變?cè)龃髣t是由第三次透射作用導(dǎo)致的,厚度小時(shí)壓力波在介質(zhì)2中傳播多次才有一次從介質(zhì)3中傳播回來(lái)的波,但第一次從介質(zhì)3傳播回來(lái)的波壓力峰值最大,而且由于邊界Ⅲ剛性,傳播回來(lái)的波是原壓力的二倍,隨著介質(zhì)2的厚度增大,當(dāng)這個(gè)波成為第三個(gè)傳播回介質(zhì)1的波時(shí),壓力峰值就會(huì)出現(xiàn)突變。對(duì)于氣背和水背邊界第一次從介質(zhì)3傳播回來(lái)的波相位相反,疊加作用使波的峰值減小,不會(huì)出現(xiàn)壓力波峰值突變的作用,峰值隨厚度減小的原理同剛性邊界原理。
5 結(jié) 論
本文基于波動(dòng)理論對(duì)一維波在覆蓋層-鋼板中的傳播情況進(jìn)行了理論推導(dǎo),得到了波在3層介質(zhì)中傳播的一維時(shí)域解析解,計(jì)算了輸入為指數(shù)衰減波時(shí)濕表面壓力的時(shí)域解析結(jié)果。同時(shí),針對(duì)輸入為指數(shù)衰減波的情況,該方法的結(jié)果通過(guò)與有限元的結(jié)果的對(duì)比證明了該方法的正確性。將該方法的結(jié)果與只計(jì)一、兩次反射透射影響的近似結(jié)果進(jìn)行了對(duì)比,結(jié)果發(fā)現(xiàn),對(duì)于剛性邊界條件,精確結(jié)果與近似結(jié)果吻合較好;對(duì)于氣背邊界和水背邊界,近似結(jié)果誤差較大。對(duì)指數(shù)衰減波進(jìn)行無(wú)量綱化,分析了改變覆蓋層的厚度、特性阻抗以及指數(shù)衰減波的衰減時(shí)間常數(shù)對(duì)結(jié)果的影響。分析結(jié)果表明,當(dāng)覆蓋層的特性阻抗減小時(shí),壓力波峰值先減小后增大再減小;覆蓋層的厚度增大,會(huì)使壓力波峰值減小(對(duì)于剛性邊界壓力波峰值先減小后突變?cè)龃笤贉p小),衰減速度快,會(huì)使壓力波峰值減小。
[1] Graff K F. Wave motion in elastic solids [M]. Dover Publications Inc., New York, 1975.
[2] Cremer L, Heckel M, Petersson B A T. Structure-borne sound [M]. Third ed., Springer, Berlin, 2005.
[3] Mace B R, Duhamel D, Brennan M J, et al. Finite element prediction of wave motion instructural waveguides [J]. Journal of the Acoustical Society of America,2005, 117(5): 2835-2843.
[4] Duhamel D, Mace B R, Brennan M J. Finite element analysis of the vibrations of waveguides and periodic structures[J]. Journal of Sound and Vibration,2006, 294 (1-2):205-220.
[5] Mace B J, Manconi E. Modelling wave propagation in two-dimensional structures using finite element analysis [J]. Journal of Sound and Vibration,2008, 318(4-5):884-902.
[6] Renno J M, Mace B R. On the forced response of wave guides using the wave and finite element method [J]. Journal of Sound and Vibration,2010, 329(26):5474-5488.
[7] Renno J M, Mace B R. Calculating the forced response of two-dimensional homogeneous media using the wave and finite element method [J]. Journal of Sound and Vibration,2011, 330:5913-5927.
[8] Akyurtlu A, Werner D H. BI-FDTD: a novel finite-difference time-domain formulation for modeling wave propagation in bi-isotropic media [J]. IEEE Trans. Antenn. Propag,2004, 52(2):416-425.
[9] Gandhi O P, Gao B Q, Chen J Y. A frequency-dependent finite difference time-domain formulation for general dispersive media [J]. IEEE Trans. Microw. Theory Tech,1993, 41:658-664.
[10] Luebbers R, Hunsberger F P, Kunz K, et al. A frequency-dependent finite-difference time-domain formulation for dispersive materials [J]. IEEE Trans. Electromagn. Comp,1990, 32:222-227.
[11] Taflove A. Review of the formulation and applications of the finite-difference time-domain method for numerical modeling of electromagnetic wave interactions with arbitrary structures [J]. Wave Motion,1988,1(6):547-582.
[12] Bathe K J, Wilson E L. Numerical methods in finite element analysis[M]. Prentice-Hall, New York, 1976.
[13] Givoli D. Recent advances in the DtN FE method[J]. Arch. Comput. Methods Eng.,1999,6(2):71-116.
[14] Givoli D. Nonreflecting boundary-conditions [J]. J. Comput. Phys,1991,94(1):1-29.
[15] Zienkiewicz O C, Taylor R L. The finite element method [J]. McGraw-Hill, NY, 1991.
[16] Desceliers C, Soize C, Grimal Q, et al. A time-domain method to solve transient elastic wave propagation in a multilayer medium with a hybrid spectral-finite element space approximation[J]. Wave Motion,2008,45(4):383-399.
[17] Brasek T P. Effect of surface coating on one-dimensional system subjected to unit step pressure wave [D]. California: Naval postgraduate School, NPS-ME-94-006, 1994.
[18] Brasek T P. Response of dual-layered structures subjected to shock pressure wave [D]. California: Naval Postgraduate School, 1994.
[19] Neilson H C, Everstine G C, Wang Y E. Transient response of a submerged fluid-coupled double-walled shell structure to a pressure pulse [J]. Journal of the Acoustic Society of America, 1981,70:1776-1782.
[20] Bergersen J K L. Effect of surface coating on cylinders subjected to underwater shock [D]. Naval postgraduate School, Monterey, California, 1992.
[21] Tayor G I. The pressure and impulse of submarine explosion waves on plates [J]. In: Underwater Explosion Research, Vol. I, Office of Naval Research, 1950:1155-1173.
[22] Snay H G, Christian E A. The response of air-backed plates to high-amplitude underwater shockwaves[R]. NAVORD, Report 2462,1952.
[23] Schechter R S, Bort R L. The response of two fluid-coupled plates to an incident pressure pulse [R]. Naval Research Laboratory, Memorandum report 4647, 1981.
[24] Huang H. A qualitative appraisal of the doubly asymptotic approximation for transient analysis of submerged structures excited by weak shock waves [R]. AD-A015941, 1975.
[25] 童宗鵬.艦船抗沖瓦結(jié)構(gòu)流固耦合建模及水下抗爆機(jī)理研究[D].上海:上海交通大學(xué),2006.
[26] 諶勇,張志誼,華宏星,等.彈性泡沫夾芯結(jié)構(gòu)的水下爆炸響應(yīng)分析[J].振動(dòng)與沖擊,2009, 28(11):25-29.
CHEN Yong,ZHANG Zhi-yi,HUA Hong-xing, et al. Analytic model for the response to water blast of one-dimensional naval structure with elastic foam coatings [J]. Journal of Vibration and Shock, 2009, 28(11):25-29.

