基于CPU-GPU異構(gòu)平臺的高層結(jié)構(gòu)地震響應(yīng)分析方法研究

李紅豫，滕 軍，李祚華

(哈爾濱工業(yè)大學(xué) 深圳研究生院，廣東 深圳 518055)

我國是地震多發(fā)的國家，需要對工程結(jié)構(gòu)進(jìn)行地震響應(yīng)分析來確保結(jié)構(gòu)在地震作用下有足夠的抗震安全性能。隨著工程結(jié)構(gòu)朝著大型化、復(fù)雜化發(fā)展，對工程結(jié)構(gòu)抗震分析的計(jì)算精度和速度要求日益提高。然而傳統(tǒng)的有限元分析方法均是基于CPU(Central Processor Unit，中央處理器)串行平臺，大規(guī)模計(jì)算在串行平臺上耗時長、精度低成為結(jié)構(gòu)有限元分析的主要障礙。并行計(jì)算可以有效解決以上弊端，能在合理的時間內(nèi)滿足精度要求完成大型結(jié)構(gòu)的分析。目前，大規(guī)模并行計(jì)算普遍采用基于MPI的集群并行系統(tǒng)，但是這種并行計(jì)算體系龐大復(fù)雜、價格昂貴、可擴(kuò)展性差，因此在地震工程中的應(yīng)用受到限制。

近年來，GPU(Graphics Processor Unit，圖形處理器)已大大超過摩爾定律的速度高速發(fā)展。由于GPU具有強(qiáng)大的并行計(jì)算能力，基于GPU平臺的高性能并行計(jì)算已經(jīng)成為國內(nèi)外研究的熱點(diǎn)[1-4]。2007年NVIDIA公司發(fā)布的CUDA(Compute Unified Device Architecture，計(jì)算統(tǒng)一設(shè)備架構(gòu))可以有效控制GPU進(jìn)行編程。這種基于GPU的編程方法給我們解決并行計(jì)算問題提供了一種新的思路。

目前，基于GPU的有限元計(jì)算應(yīng)用的研究仍處于初級階段，研究主要集中于有限元靜力問題中涉及大型稀疏線性系統(tǒng)問題的并行計(jì)算方法上[5-9]，對于結(jié)構(gòu)有限元動力計(jì)算問題研究較少。

本文基于CUDA架構(gòu)建立了適用于結(jié)構(gòu)有限元分析的CPU-GPU異構(gòu)平臺。在該平臺上研究基于GPU的高層結(jié)構(gòu)地震響應(yīng)分析算法。通過空間框架結(jié)構(gòu)的算例，驗(yàn)證了本文所提方法在保證計(jì)算高精度的條件下，相比傳統(tǒng)CPU串行方法具有較高提速性能。

1 CPU-GPU異構(gòu)平臺構(gòu)建

所謂CPU-GPU異構(gòu)平臺，是指由CPU和GPU兩個不同的架構(gòu)共同協(xié)同工作來解決同一個問題的計(jì)算平臺。實(shí)現(xiàn)這個異構(gòu)計(jì)算系統(tǒng)，需要通過CUDA架構(gòu)來搭建。

CUDA是專門針對GPU來進(jìn)行編程的架構(gòu)，這與以往單獨(dú)在CPU上串行計(jì)算有本質(zhì)上的區(qū)別。以往的CPU串行計(jì)算只是針對一個處理器，而CUDA是針對GPU的。程序架構(gòu)的原則是依據(jù)CPU和GPU各自的優(yōu)勢特點(diǎn)來區(qū)分，即CPU負(fù)責(zé)進(jìn)行邏輯判斷和串行計(jì)算相關(guān)工作，GPU則主要負(fù)責(zé)線程間高度并行的數(shù)據(jù)處理工作。因此在CUDA的架構(gòu)下，一旦確定了程序中的并行部分，程序代碼就可以分為兩大部分：一部分交給CPU處理，另外一部分交給GPU處理。CUDA架構(gòu)中是將CPU作為主控制器，稱為主機(jī)(Host)；GPU作為協(xié)處理器，稱為設(shè)備(Device)。在GPU上執(zhí)行的程序稱為內(nèi)核函數(shù)(kernel)。一個kernel函數(shù)對應(yīng)一個網(wǎng)格(grid)，一個grid由若干個線程塊(block)組成，一個block由若干個線程(thread)組成，thread是最終數(shù)據(jù)的承載者，在各個block之間并行執(zhí)行。

CUDA程序的執(zhí)行過程如圖1所示，大致包括以下四個步驟：

圖1 CUDA程序執(zhí)行過程

(1) CPU上的串行代碼完成必要的GPU上的數(shù)據(jù)準(zhǔn)備和初始化工作；

(2) 將待運(yùn)算的數(shù)據(jù)從CPU內(nèi)存中復(fù)制傳輸?shù)紾PU顯存中；

(3) 啟動kernel函數(shù)和CUBLAS庫函數(shù)，在GPU執(zhí)行線程級的并行運(yùn)算任務(wù)；

(4) GPU計(jì)算完成后，將得到的結(jié)果拷貝回CPU內(nèi)存中。

2 CPU-GPU異構(gòu)平臺上結(jié)構(gòu)地震響應(yīng)算法實(shí)現(xiàn)

結(jié)構(gòu)體系的動力平衡方程以矩陣形式給出如下：

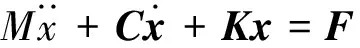
(1)

(1) 初始計(jì)算

① 計(jì)算積分常數(shù)

a0=1/(βΔt2),a1=γ/(βΔt),a2=t/(βΔt)

a3=1/(2β)-1,a4=γ/β-1,

a5=(γ/(2β)-1)Δt

② 計(jì)算等效剛度矩陣

K*=K+a0M+a1C

(2)

③ 解線性方程，求解初始加速度

(3)

(2) 計(jì)算t+Δt時刻的響應(yīng)

① 計(jì)算參數(shù)向量

(4)

(5)

② 計(jì)算等效荷載向量

(6)

③解線性方程，求解t+Δt時刻的位移向量

(7)

④ 計(jì)算t+Δt時刻的速度向量和加速度向量

(8)

(9)

由以上Newmark-β的計(jì)算步驟可以看出，計(jì)算工作量主要集中在求解每一時間步t+Δt的響應(yīng)，對于大規(guī)模計(jì)算，若采用普通的串行方法求解，將消耗大量的計(jì)算時間。基于本文構(gòu)建的CPU-GPU異構(gòu)平臺，本文提出基于GPU的Newmark-β法的并行求解策略，如圖2所示。整體思路如下：除了初始計(jì)算，即剛度矩陣K、質(zhì)量矩陣M、阻尼矩陣C以及等效剛度矩陣K*在CPU中計(jì)算完成以外，每一個時間步的響應(yīng)都在GPU中計(jì)算完成，該方法通過編制CUDA程序，調(diào)用kernel函數(shù)和CUBLAS庫函數(shù)實(shí)現(xiàn)。

GPU中負(fù)責(zé)完成的并行計(jì)算如圖2中陰影部分所示，包括以下計(jì)算步驟：

(1) 由參數(shù)向量ct和dt得到等效荷載向量F*；

(2) 求解線性方程組獲得當(dāng)前時間步下的位移向量xt+Δt；

(4) 重復(fù)以上步驟，直到整個時間步循環(huán)在GPU中計(jì)算完成。

圖2 基于GPU的Newmark-β算法

目前求解線性方程組的常用方法是直接法，如高斯消元法。該方法依賴于整體剛度矩陣的存儲方式，分解過程會出現(xiàn)“填充”，不能充分利用整體剛度矩陣稀疏帶狀的特性。隨著問題規(guī)模的擴(kuò)大，這種存儲要求可能成為瓶頸。相比直接法，迭代法有更多的優(yōu)勢：其占用存儲空間小，每次迭代從頭開始，不會產(chǎn)生誤差累積，精度有保障。其中CG法(Conjugate Gradient，共軛梯度迭代法)由于內(nèi)在的并行性，在求解線性方程組中經(jīng)常采用。但系數(shù)矩陣的條件數(shù)很大程度上制約了共軛梯度法的收斂性，所以一般須對原有方程組進(jìn)行預(yù)條件處理，即PCG法(Preconditioning Conjugate Gradient，預(yù)處理共軛梯度迭代法)。

由于PCG法的計(jì)算優(yōu)勢，本文提出了基于GPU的PCG并行算法，用來加速線性方程組的求解。在PCG算法中，每個循環(huán)迭代包含稀疏矩陣-向量乘、點(diǎn)積和向量更新這三種數(shù)據(jù)操作。這些操作由于具有內(nèi)在并行性，因此PCG法的迭代過程可以在GPU上實(shí)現(xiàn)，算法流程如圖3所示，其中陰影部分是指在GPU中進(jìn)行的計(jì)算。算法的整體思路如下：CPU負(fù)責(zé)初始化計(jì)算和迭代收斂準(zhǔn)則的判斷，GPU負(fù)責(zé)稀疏矩陣-向量乘、點(diǎn)積和向量更新的并行計(jì)算。在GPU中計(jì)算獲得方程組的解之后，從GPU調(diào)出數(shù)據(jù)到CPU，接著CPU進(jìn)行數(shù)據(jù)輸出等后處理操作。針對本文提出的基于GPU的Newmark-β算法，在GPU中完成PCG法迭代收斂，得到方程組的解，即得到該時間步下的位移向量后，緊接著繼續(xù)在GPU中求解速度和加速度。

圖3 基于GPU的PCG法

3 數(shù)值實(shí)驗(yàn)

3.1 平臺參數(shù)

計(jì)算平臺CPU為Intel i5-2300，頻率為2.8 GHz，內(nèi)存為4.00 GB；GPU為NVIDIA GeForce GTX 460，336個CUDA cores，計(jì)算能力2.1，流處理器頻率為1.4 GHz，顯存為1.0 GB，顯存帶寬為115.2 GB/s。

3.2 計(jì)算模型

分別在傳統(tǒng)的CPU串行平臺和本文構(gòu)建的CPU-GPU異構(gòu)平臺上，以三維梁單元的大規(guī)模有限元模型進(jìn)行數(shù)值實(shí)驗(yàn)。設(shè)計(jì)了3個類型共33個空間框架結(jié)構(gòu)計(jì)算模型，框架編號為Fi-j-k，其中F表示框架(Frame)，i表示框架樓層數(shù)，j表示沿建筑長方向(設(shè)為X方向)的跨數(shù)，k表示沿建筑寬方向(設(shè)為Y方向)的跨數(shù)。各類型結(jié)構(gòu)計(jì)算模型參數(shù)如表1所示。

表1 各類型結(jié)構(gòu)算例框架自由度數(shù)

(1) 類型1(固定跨數(shù)，變化高度)

本類型空間框架計(jì)算模型，層高均為3 m，跨度為6 m，X方向5跨，Y方向5跨，通過變換樓層高度獲得不同的計(jì)算模型。

(2) 類型2(固定高度，變化跨數(shù))

本類型空間框架計(jì)算模型，層高均為3 m，層數(shù)為30層，高度為90 m，跨度為6 m，通過變換X、Y方向的跨數(shù)獲得不同的計(jì)算模型。

(3) 類型3算例(同時變化高度和跨數(shù))

本類型空間框架計(jì)算模型，層高均為3 m，跨度為6 m，通過變換樓層高度和X、Y方向的跨數(shù)獲得不同的計(jì)算模型。

3.3 模型驗(yàn)證

地震波采用El Centro(N-S)波，采樣周期0.02 s，持續(xù)時間40 s。在進(jìn)行時程分析時，將地震動加速度峰值調(diào)整為220 cm/s2，相當(dāng)于7度罕遇地震。結(jié)構(gòu)采用瑞利阻尼，阻尼比取0.05。

在CPU-GPU異構(gòu)平臺上調(diào)用kernel前需要給出執(zhí)行配置參數(shù)，定義grid以及block的維度。線程的最大值不能超過每個線程塊所允許線程數(shù)量，受限于線程的寄存器個數(shù)，對于NVIDIA GeForce GTX 460的GPU硬件設(shè)備，每個block的線程最多只能取1 024個。

為了驗(yàn)證自編程序的正確性，以類型1框架編號F10-5-5為例，將本文所提方法得到的結(jié)構(gòu)頂層位移時程曲線、速度時程曲線和加速度時程曲線與有限元軟件ABAQUS得到的計(jì)算結(jié)果進(jìn)行對比分析，對比結(jié)果如圖4和表2所示。

圖4 自編程序與ABAQUS計(jì)算結(jié)果對比

表2 F10-5-5模型結(jié)構(gòu)響應(yīng)對比

從圖4和表2中看出，自編程序得到的動力響應(yīng)與ABAQUS有限元計(jì)算結(jié)果符合較好，誤差均在3%以內(nèi)。其中，位移峰值誤差為-1.470%，相對而言，加速度峰值誤差稍大，為-2.322%。從誤差分析來看，自編程序與ABAQUS有限元計(jì)算結(jié)果相差不大，表明自編程序正確可行。

3.4 并行計(jì)算精度和效率分析

(1) 計(jì)算精度

基于CPU-GPU異構(gòu)平臺得到的計(jì)算結(jié)果與CPU串行平臺的計(jì)算結(jié)果完全一致，相對誤差均為零，計(jì)算精度很高。這表明在CPU-GPU異構(gòu)平臺上CPU和GPU端口之間的數(shù)據(jù)通信與傳遞不會造成數(shù)據(jù)丟失，能保證數(shù)據(jù)完整性；同時也驗(yàn)證了在GPU上進(jìn)行并行計(jì)算編制的kernel函數(shù)以及所選用的庫函數(shù)是準(zhǔn)確的。

(2) 計(jì)算加速比

并行計(jì)算性能常用并行加速比來衡量，加速比是表示采用采用多個處理器計(jì)算速度所能得到的加速的倍數(shù)[11]。在本文中，GPU視為CPU的協(xié)處理器，因此衡量GPU的并行計(jì)算加速比可以表示為：

Speedup=Ts/Tp

(10)

式中:Ts表示CPU串行計(jì)算耗時，Tp表示GPU并行計(jì)算耗時。

CPU串行平臺以及CPU-GPU異構(gòu)平臺的計(jì)算耗時及GPU加速比如圖5～圖7所示。

圖5 類型1算例計(jì)算耗時對比及GPU加速比

圖6 類型2算例計(jì)算耗時對比及GPU加速比

圖7 類型3算例計(jì)算耗時對比及GPU加速比

從圖5～圖7中看出，從計(jì)算耗時上來看，在CPU串行平臺上，計(jì)算耗時隨著計(jì)算規(guī)模(自由度數(shù))增加顯著增大，而在CPU-GPU異構(gòu)平臺上，計(jì)算耗時增加非常緩慢。從計(jì)算性能上來看，GPU計(jì)算加速比隨自由度數(shù)的變化趨勢是基本一致的，即當(dāng)計(jì)算規(guī)模較小(自由度數(shù)小于5 000)時，GPU加速比隨著自由度數(shù)增加基本呈線性關(guān)系，隨著自由度數(shù)增大，GPU加速比持續(xù)增大。這表明隨著計(jì)算規(guī)模擴(kuò)大，GPU的數(shù)據(jù)處理量增大，其并行處理能力也逐漸體現(xiàn)，3個類型的算例最終都獲得了25～30倍較高的加速比。

4 結(jié) 論

(1) 為解決傳統(tǒng)的串行有限元分析方法計(jì)算耗時多精度低的問題，提出了一種基于GPU并行計(jì)算能力在CUDA架構(gòu)下構(gòu)建高層結(jié)構(gòu)有限元分析的CPU-CPU的異構(gòu)平臺。

(2) 提出在GPU上并行求解結(jié)構(gòu)地震響應(yīng)，實(shí)現(xiàn)了基于GPU的Newmark-β算法。算法中對每一時間步采用基于GPU的預(yù)處理共軛梯度迭代法求解線性方程組，有效減少計(jì)算時間，提高計(jì)算效率。

(3) 通過對比分析本文提出的方法與ABAQUS軟件得到的計(jì)算結(jié)果，自編程序與ABAQUS有限元計(jì)算結(jié)果相差甚小，驗(yàn)證了自編程序的正確可行。

(4) 在CPU-GPU異構(gòu)平臺上進(jìn)行的數(shù)值算例表明，本文所提方法在保證計(jì)算高精度的條件下，相比傳統(tǒng)CPU串行方法具有較高提速性能。

(5) 鑒于GPU架構(gòu)不斷更新，本文建立的異構(gòu)平臺可以取得更高的并行效率，因此本文提出的算法可推廣利用到規(guī)模更大更復(fù)雜的結(jié)構(gòu)有限元動力計(jì)算問題中去。

[1] Bolz J, Farmer I, Grinspun E, et al. Sparse matrix solvers on the GPU: Conjugate gradients and multigrid[J]. ACM TRANSACTIONS ON GRAPHICS, 2003, 22(3): 917-924.

[2] Harris M J, Baxter III W V, Scheuermann T, et al. Simulation of cloud dynamics on graphics hardware[C]. Proceedings of the ACM SIGGRAPH/EUROGRAPHICS conference on Graphics hardware, San Diego, CA, USA, 2003: 92-101.

[3] Georgescu S, Okuda H. Conjugate gradients on multiple GPUs[J]. International Journal for Numerical Methods in Fluids, 2010, 64(10-12): 1254-1273.

[4] Zuo W, Chen Q. Fast and informative flow simulations in a building by using fast fluid dynamics model on graphics processing unit[J]. Building and Environment, 2010, 45(3): 747-757.

[5] Filelis-Papadopoulos C K, Gravvanis G A, Matskanidis P I, et al. On the GPGPU parallelization issues of finite element approximate inverse preconditioning[J]. Journal of Computational and Applied Mathematics, 2011, 236(3): 294-307.

[6] Gravvanis G, Filelis-Papadopoulos C, Giannoutakis K. Solving finite difference linear systems on GPUs: CUDA based Parallel Explicit Preconditioned Biconjugate Conjugate Gradient type Methods[J]. The Journal of Supercomputing, 2012, 61(3): 590-604.

[7] Helfenstein R, Koko J. Parallel preconditioned conjugate gradient algorithm on GPU[J]. Journal of Computational and Applied Mathematics, 2012, 236(15): 3584-3590.

[8] Kiss I, Gyim thy S, Badics Z, et al. Parallel Realization of the Element-by-Element FEM Technique by CUDA[J]. IEEE Transactions on Magnetics, 2012, 48(2): 507-510.

[9] Yan D, Cao H, Dong X, et al. Optimizing algorithm of sparse linear systems on GPU[C].2011 Sixth ChinaGrid Annual Conference, Liaoning, China, 2011: 174-179.

[10] 鄧紹忠，周樹荃. 有限元結(jié)構(gòu)分析并行計(jì)算的若干研究進(jìn)展[J]. 南京航空航天大學(xué)學(xué)報(bào)，1995，27(1)：27-32.

DENG Shao-zhong, ZHOU Shu-quan. Some recent advances in the parallel computation of finite element structural analysis [J]. Journal of Nanjing University of Aeronautics and Astronautics, 1995, 27(1): 27-32.

[11] 張偉偉，金先龍，曹露芬，等. 公鐵兩用隧道動態(tài)響應(yīng)并行計(jì)算分析[J]. 振動與沖擊，2012，31(8)：164-169，175.

ZHANG Wei-wei, JIN Xian-long, CAO Lu-fen, et al. Dynamic response analysis for a highway-railway double-duty tunnel using parallel computing [J]. Journal of Vibration and Shock,2012, 31(8): 164-169, 175.