波導終端短路法測量固體材料的電容率

栗佳佳，金 瑞，張志華，杜 艾，方 愷，赫 麗

(同濟大學 物理科學與工程學院，上海 200092)

1 引 言

微波介質材料的電容率[1]，是研究材料的微波特性和設計微波器件的重要參量. 微波工程中廣泛應用各種電介質材料，如同軸線中的絕緣片、微波集成電路的介質基片、波導中的介質片以及介質天線中各種微波器件的支持裝置等. 因此，在微波波段研究介質特性參量測量原理和方法[2-3]有著實際的意義. 文獻[1]著重探究了波導終端短路法測量液體材料電容率的具體過程. 本文重在探究波導終端短路法測量固體物質電容率的可行性并探究最適填充長度，通過微波網絡分析儀對測試結果進行了對比和驗證.

2 實驗原理

波導法是將填充介質試樣的波導段作為傳輸系統的一部分來測量它的復數相對電容率εr. 具體測量方法可以分為傳輸法和反射法. 反射法是最常用的方法.

波導法測量介質的εr實際上是阻抗測量的具體應用,這種方法中，介質試樣段接在測量系統的末端，它的輸出端接短路器或開路器(即λg/4短路器)，以產生全反射波. 圖1顯示了終端短路法的測量原理示意圖. 根據介質試樣段引起的駐波節點偏移和駐波比，可確定介質的相對電容率. 當介質的損耗極小而可以看成無耗介質時，用該方法可以獲得準確的結果.

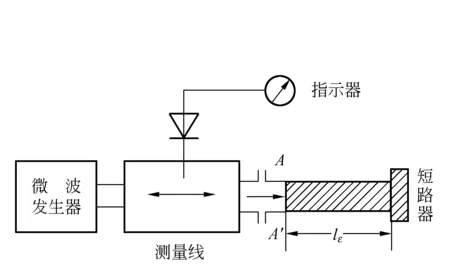
圖1 終端短路法測量原理

在裝有介質試樣的終端短路波導中，從介質試樣的輸入端面向終端看，輸入的等效阻抗為

Z1=Z0εtanh (γ)lε,

(1)

(2)

式中，Z0為空氣波導的特性阻抗，β0=2π/λg為在空氣波導中的相位系數，λg為未放入介質試樣的波導波長,ρ為介質試樣段的輸入駐波比. 于是，得到阻抗關系方程為

(3)

(4)

在傳輸H10波的矩形波導測量系統中,復數相對電容率可按下式計算：

(5)

式中，λ0為未放入介質試樣的波導波長，為自由空間波長(可通過未填充介質的空氣波導中測量頻率來計算)，a為波導的寬邊尺寸.

(6)

(7)

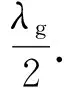
圖2 確定的方法

當衰減常量α遠小于相位常量β時，采取近似解法. 將式(4)右邊寫成A+jB的形式：

(8)

可得

(9)

(10)

γlε=α+jβ=a+jb,

(11)

則可化簡為

(12)

得

(13)

(14)

對于損耗小的電介質，設a=0，則A可近似為

(15)

b′為a=0時的近似值b.

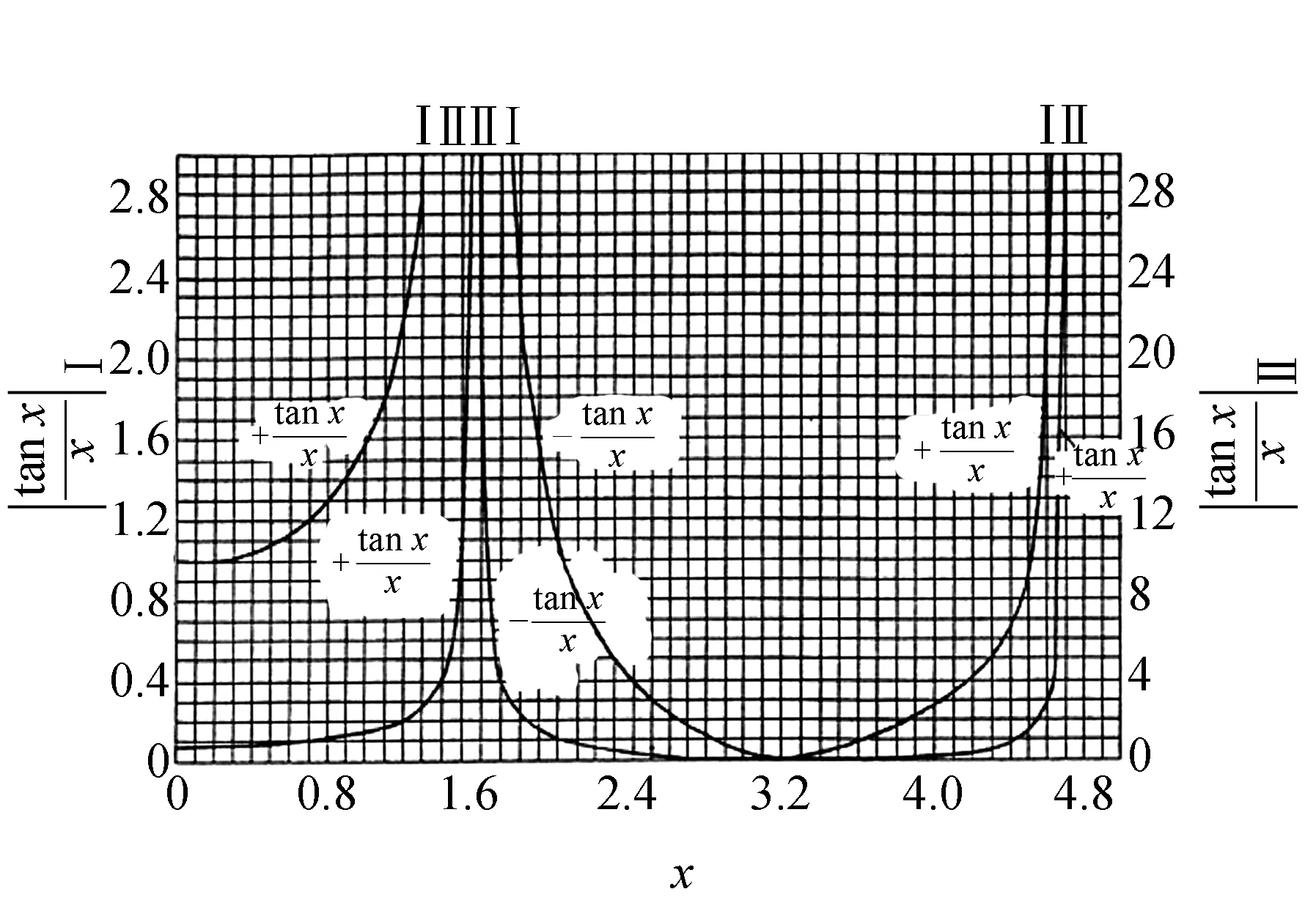
圖3 函數與x關系曲線圖

再設a很小，則B可近似為

(16)

得出：

(17)

按(5)式計算介質材料的相對電容率.

3 實驗內容

實驗按下述步驟測量不同長度介質的電容率. 微波頻率為9.37 GHz.

a.將波導終端短路，用極小點附近兩點坐標的平均值法測出波導波長λg[5]；

b.確定測量線的零點坐標刻度，d=0,左移測量線，用極小點附近兩點坐標平均值法確定左鄰駐波節點刻度dT；

c.取下短路器，放入被測介質試樣,裝上短路器，左移測量線，用極小點附近兩點坐標平均值法確定左鄰駐波節點刻度dε，同時測出駐波系數ρ0；

d.按c步驟重復測量不同長度介質試樣的左鄰駐波節點刻度dε，駐波系數ρ0；

e.按c和d步驟測量另一種介質試樣不同長度的左鄰駐波節點刻度dε，駐波系數ρ0；

f.用上述實驗數據計算求出固體介質材料的相對電容率εr.

同時使用Agilent N5222A PNA微波網絡分析儀配備85070E介電探頭套件對樣品進行相對電容率測試驗證，儀器測試頻率范圍10 MHz～26.5 GHz，探頭支持200 MHz～50 GHz的頻率范圍.

4 實驗結果與分析

4.1 橡皮擦(聚氯乙烯)材料的介電性能

將橡皮檫(聚氯乙烯)材料填充進波導段，并不斷改變填充長度，利用終端短路法進行數據采集，并通過計算得出介質的電容率. 實驗數據如表1所示.

表1 橡皮檫(聚氯乙烯)材料實驗數據

實驗數據處理如下:

(9)式化簡為

(10)式B≈0,代入數據得到A值.

即傳播常量只存在虛部為

γ=iβ,

(18)

即得到如表2所示的電容率與填充入波導材料長度的關系.

橡皮擦是由聚氯乙烯軟化加入塑型劑制成，通過查閱資料[6]得知聚氯乙烯電容率約為3.5～5. 由表2中數據可知當lε為12 mm即約為1/4波長(12.84 mm)時，所測結果數據3.69準確.

由橡皮檫材料實驗數據可知填充入材料長度因前后界面對波傳播產生諸如反射等因素而影響測量結果. 當填充材料厚度是波長的1/4時，前后界面反射光的光程差恰好為π，即振動方向相反，疊加的結果使材料界面對該波長的反射光減少，使波無損耗地通過材料傳播到達短路板后反射形成近純駐波.

表2 橡皮檫(聚氯乙烯)材料計算數據

通過Agilent N5222A PNA微波網絡分析儀配備85070E介電探頭套件進行數據驗證，實驗微波頻率范圍0.5～15 GHz，橡皮檫材料電容率數據如圖4所示.

由圖4可得在實驗所用微波頻率9.37 GHz

附近，如9.35 GHz得到電容率3.77，9.38 GHz得到電容率3.74，介于理論值3.5～5間. 而實驗測得填充長度為1/4波長時電容率值3.69，與儀器驗證值在誤差允許范圍內符合，因此再次驗證填充長度為1/4波長為最適填充長度. 說明波導終端短路法適合測量固體物質的電容率.

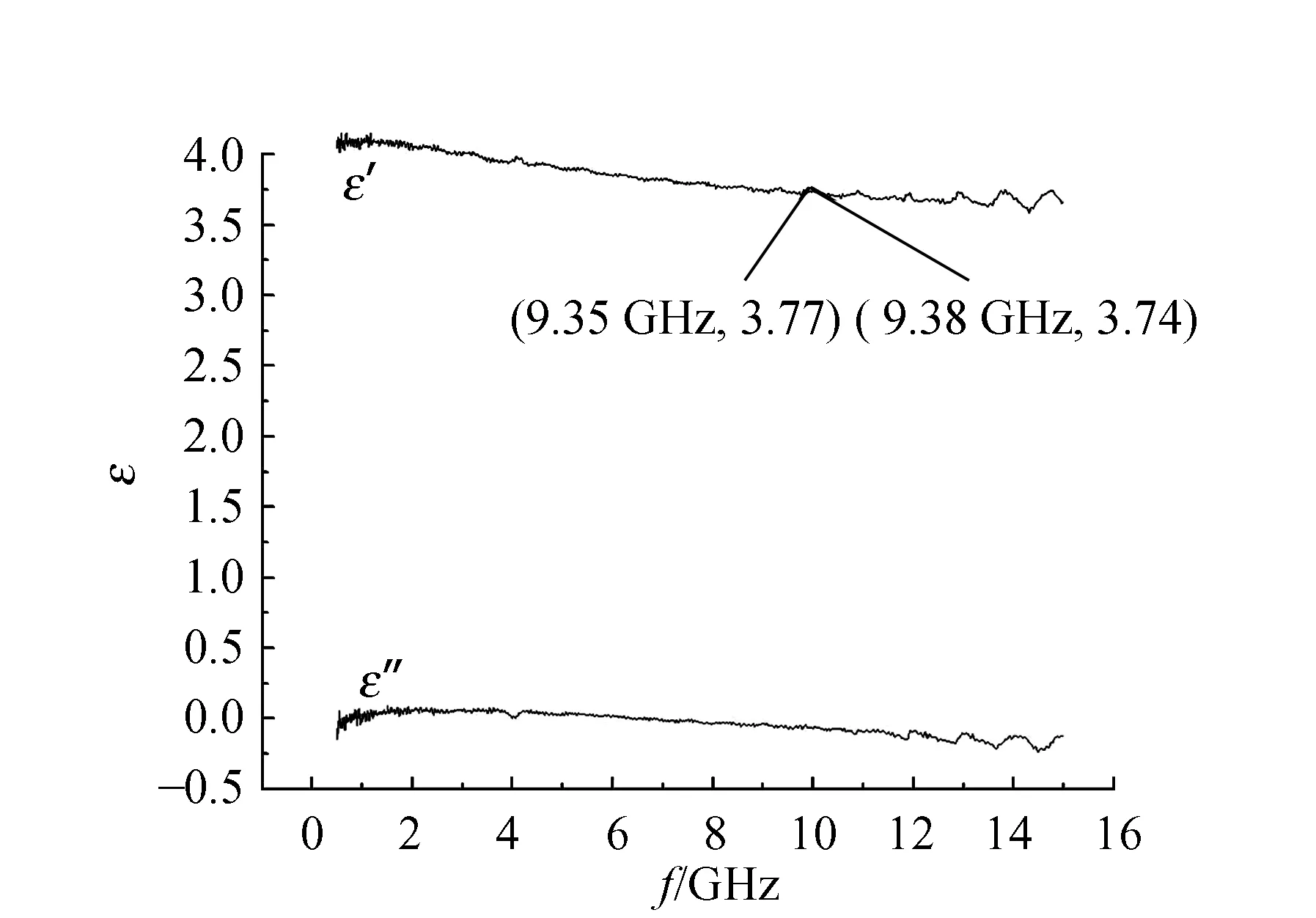
圖4 橡皮檫(聚氯乙烯)電容率-微波頻率圖

4.2 塑料板(聚乙烯)、擠塑板(聚苯乙烯)材料的介電性能

同樣將塑料板(聚乙烯)、擠塑板(聚苯乙烯)填充進波導段，由于材料不易制備，根據前面的實驗測試結果故只選取1/4波長長度的材料進行填充，利用終端短路法進行數據采集，并計算得出介質的電容率. 實驗數據如表3所示. 計算得到表4的結果.

表3 塑料板(聚乙烯)、擠塑板(聚苯乙烯)材料實驗數據

表4 塑料板(聚乙烯)、擠塑板(聚苯乙烯)材料計算數據

通過查閱資料[6]得知聚乙烯材料的電容率為2.2～2.4. 根據表4中數據可知所測結果塑料板的電容率2.45在理論誤差之內，符合理論值.

通過查閱資料[6]得知聚苯乙烯的電容率為2.4～2.6. 根據表4中數據可知所測結果擠塑板的電容率2.87，和理論接近.

由擠塑板材料數據可知，擠塑板因填充后易產生形變，導致其微結構改變，對電容率影響較大. 而擠塑板在制作過程中難以保證反射面平整，減反過程不理想，使實驗結果產生誤差. 因此在后續實驗探索中應注意保持材料原始形狀，并尋找更好的材料制作填充方法. 并且應減小數據梯度，增加數據數量,簡化實驗步驟，提高實驗準確性.

實驗中出現純駐波現象而得到的駐波比為無窮，可知傳播常量只包含虛部部分. 說明實驗過程操作得當，材料儀器較理想，短路片與介質材料的等效阻抗不存在與空氣介質匹配現象. 波傳播過程中不存在損耗現象，而只產生相位移動.

5 結束語

證明了終端短路法測量固體介質電容率的可行性，但對填充介質有一定要求，材料填充后應盡量保持原始形狀，更好的材料制作填充方法有待繼續探究[7-8]. 實驗同時得到了最適填充長度為1/4波長，并根據波傳播機制進行了合理的推斷.

參考文獻：

[1] 鄧京川，王魁香. 液體介電常數的微波測量[J]. 物理實驗,1996,16(3):104-105.

[2] 董鍵，崔秀芝. 波導管中微波波長測量方法的研究[J]. 物理實驗，2013，33(8)：30-33.

[3] 吳毅強，廖昆明，陳力，等. 基于曲面擬合無損測量復介電常數方法[J]. 固體電子學研究與進展，2012,32(5):493-496.

[4] 馬洪良，張義邴. 近代物理實驗[M]. 上海：上海大學出版社，2012：161-167.

[5] 同濟大學物理實驗中心. 近代物理實驗講義[Z]. 2013:185-188.

[6] 姚允斌，解濤，高英敏. 物理化學手冊[M]. 上海：上海科學技術出版社，1985：213.

[7] 費彬城,陳良雷，陳余行，等. 雙面金屬鋁包覆介質波導測量介質厚度和折射率[J]. 大學物理實驗，2013，26(1)：1-3.

[8] 徐江峰，陳秋靈，倪爾瑚. 截止波導介質腔介電常數測量理論與方法研究[J]. 儀器儀表學報，2006，27(10)：1322-1325.