能源混沌系統的主動滑模同步控制

徐瑞萍，劉振

1.青島大學數學科學學院，山東青島 266071

2.中國海洋大學數學科學學院，山東青島 266100

◎工程與應用◎

能源混沌系統的主動滑模同步控制

徐瑞萍1，劉振2

1.青島大學數學科學學院，山東青島 266071

2.中國海洋大學數學科學學院，山東青島 266100

研究了一類能源混沌系統的同步問題。基于主動控制理論與滑模控制理論，給出了一種主動滑模控制器的設計方案。由于閉環誤差系統依賴于控制器的參數，所以可通過調節這些參數使誤差系統漸近穩定，從而實現了能源混沌系統的漸近同步。數值仿真結果說明了所設計方法的有效性與可行性。

混沌；同步；能源系統；主動滑模控制

1 引言

近年來，混沌系統的同步得到研究者和技術人員的廣泛關注[1-5]。在過去的20年里，人們提出了許多實現混沌系統同步的方法，如反饋方法、自適應方法、主動控制方法、滑模控制方法、主動滑模控制法等[6-10]。混沌同步不但在化學反應、保密通信、生物醫學、信息過程[11-12]等領域有很大的應用潛力和發展前景，隨著經濟的不斷發展，能源的供應和需求問題也得到越來越多的關注。由于能源系統在實際應用中潛在的重要性，這類混沌系統的控制和同步已成為混沌理論研究及應用中的熱點問題[13-14]。最近，文獻[15]提出了一個新的能源需求-供給動力系統，它是一個三維自治系統，具有非常復雜的動力學行為。文獻[16]利用線性反饋控制方法實現了這個系統的同步。

眾所周知，滑模控制（SMC）是一種特殊的非線性控制技術，也是一種控制非線性動力系統強有力的方法[17]，SMC的主要特點是對內部參數的不確定性和外部擾動都具有很強的魯棒性。主動控制技術可以消除系統的非線性項。本文結合主動控制和滑模控制技術，設計了一種主動滑模控制器，通過選擇合適的控制器參數使得誤差系統漸近穩定，從而實現能源混沌系統的同步。

2 系統描述

考慮文獻[15]提出的能源系統：

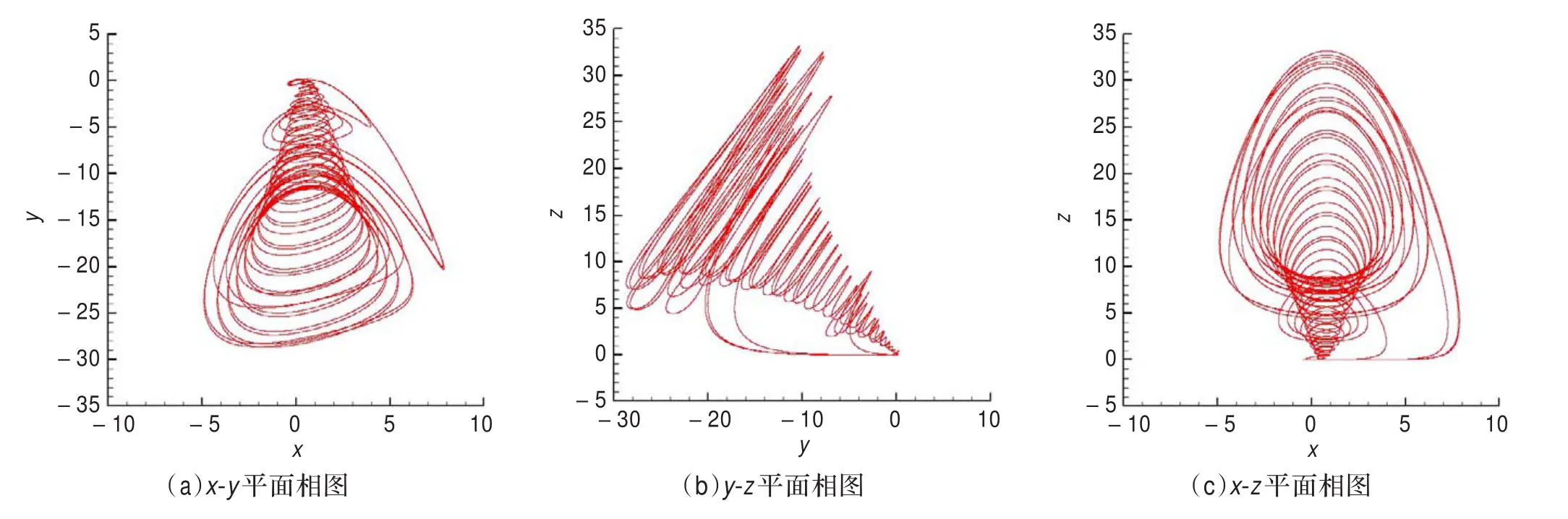
圖1 能源系統式（1）的混沌吸引子

3 主動滑模控制器的設計和分析

主動滑模控制器是主動控制器和滑模控制器的結合，下面分別給出它們的設計方法。

3.1 主動控制器的設計

設有驅動系統和響應系統，分別用(x1，y1，z1)和(x2，y2，z2)表示其狀態向量。驅動系統的狀態方程表示為：

其中a3=a1/M，b4=b3N，d1=c1c3，d2=c1c2。因此，系統式（2）與式（3）的同步問題，轉化為系統式（5）的穩定性問題，即

根據主動控制設計程序，選擇控制輸入u(t)∈R3用來消除誤差動力系統式（5）的非線性部分，即選擇如下的主動控制函數：

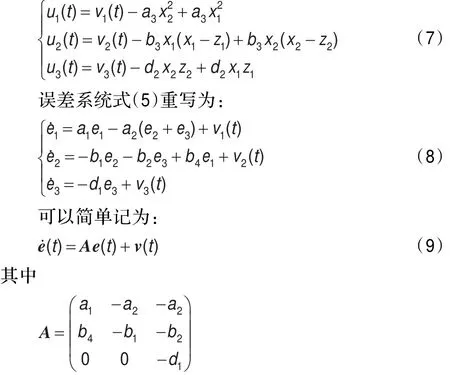
v(t)=(v1(t)，v2(t)，v3(t))T。方程（9）是帶有新控制輸入v(t)∈R3的誤差系統。關于控制v(t)的選取有許多方法，此處選滑模變結構控制：

其中h=(h1，h2，h3)T是常向量，w(t)∈R是控制輸入且滿足：

其中s=s(e)是切換函數。將式（10）代入方程（9），可得誤差系統：

3.2 滑模面的設計

選取切換面：

基于文獻[17]中的等效控制法，在滑模面上應滿足：

因此只要選取合適的C，h，使系統式（18）具有負實部的特征根，就能保證滑模運動是漸近穩定的。

3.3 滑模控制器的設計

下面選擇合適的控制器使得誤差系統的軌線都能在有限時間內到達滑模面。所選控制器應滿足到達條件s＜0，利用文獻[18]中提出的雙冪次趨近律：

其中sgn(·)表示符號函數，α＞1， 0＜β＜1，k1＞0，k2＞0是增益。當系統狀態遠離滑動模態(|s|＞1)時，式（19）中第1項起主導作用；當系統狀態接近滑動模態(|s|＜1)時，第2項起主導作用，兩項結合可以保證系統狀態在趨近滑動模態過程中的運動品質。

由式（12）和（13）得：

3.4 穩定性分析

定理對于系統式（22），在控制器式（21）的作用下，誤差系統是漸近穩定的。即在控制器式（21）的作用下，系統式（2）和系統式（3）達到混沌同步。

證明取Lyapunov函數：

將V沿誤差系統式（22）的軌跡對時間t求導，得：

故當k1＞0，k2＞0時，是負定的，所以誤差系統是漸近穩定的。即系統式（2）和系統式（3）達到混沌同步。證畢。

4 數值仿真

利用4階Runge-Kutta算法進行數值仿真，系統的參數取為a1=0.09，a2=0.15，b1=0.06，b2=0.082，b3=0.07，c1=0.2，c2=0.5，c3=0.4，M=1.8，N=1.0，誤差系統的初值取為(-0.5，-1.2，0.4)，控制參數取為h=[0.010.40.04]T，C=[1.05-0.281]，k1=0.6，k2= 0.2時的數值仿真圖（見圖2），從圖2可以看出，誤差系統的狀態在t=50之后，就收斂到0。系統切換面s(e)=0運動示意圖如圖3所示。系統控制器u(t)運動示意圖如圖4所示。

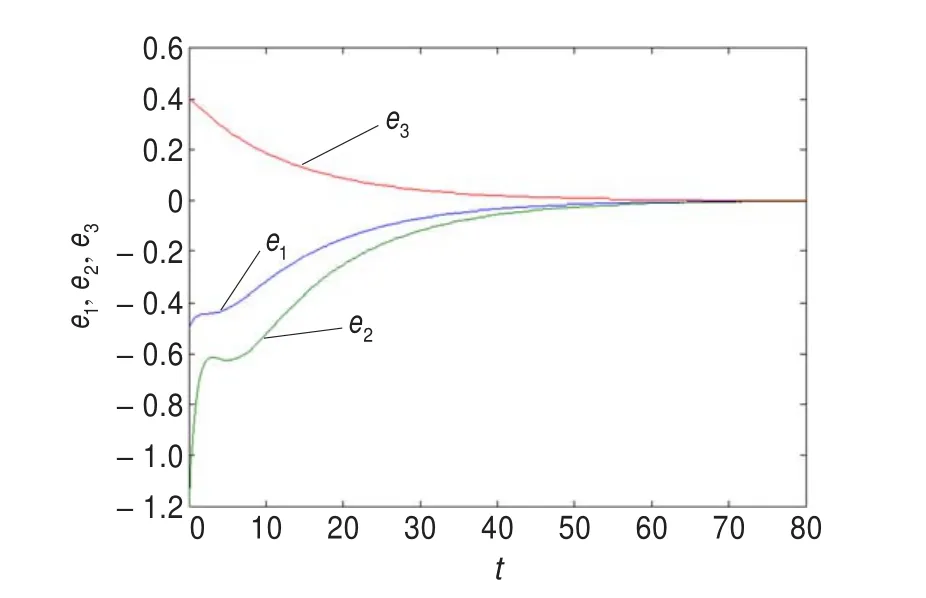
圖2 系統誤差e(t)=(e1(t)，e2(t)，e3(t))T運動示意圖

圖3 系統切換面s(e)=0運動示意圖

圖4 系統控制器u(t)運動示意圖

5 結論

本文針對文獻[15]提出的能源混沌系統，設計了一種基于雙冪次趨近律的主動滑模控制器，通過正確選擇控制器的參數使得閉環誤差系統漸近穩定，從而能源混沌系統的狀態漸近同步。因此，上述方法具有良好的理論研究意義和實際應用價值。

[1]Carroll T L，Pecora L M.Synchronizing chaotic circuits[J]. IEEE Trans on Circ Syst，1991，38：453-456.

[2]Chen G，Dong X.On feedback control of chaotic continuous-time systems[J].IEEE Trans on Circ Syst，1993，40：591-601.

[3]An X L，Yu J N，Li Y Z.Design of a new multistage chaos synchronized system for secure communications and study on noise perturbation[J].Mathematical and Computer Modelling，2011，54：7-18.

[4]Cao J，Li H X.Synchronization criteria of Lur’e systems with time-delay feedback control[J].Chaos，Solitons and Fractals，2005，23：1285-1298.

[5]Ghosh D，Chowdhury A R，Saha P.Synchronization error estimation and controller design for delayed lur’e systems with parameter mismatches[J].IEEE Transactions on Neural Networks and Learning Systems，2012，23（10）：1551-1563.

[6]Ma J，Wang Q Y，Jin W Y，et al.Control chaos in the hindmarsh-rose neuron by using intermittent feedback with one variable[J].Chin Phys Lett，2008，25（10）：3582-3585.

[7]Sun M，Tian L X，Jiang S，et al.Feedback control and adaptive control of the energy resource chaotic system[J]. Chaos，Solitons and Fractals，2007，32：1725-1734.

[8]張裊娜，周邃，張德江.基于主動控制的異結構混沌系統有限時間同步[J].吉林大學學報，2011，41（4）：1131-1134.

[9]Mohammad P A，Sohrab K，Ghassem A.Finite-time synchronization of two different chaotic systems with unknown parameters via sliding mode technique[J].Applied Mathematical Modelling，2011，35：3080-3091.

[10]譚文，蔣逢靈，王耀南，等.一類混沌系統的滑動模態同步控制及其應用[J].計算機工程與應用，2013，49（7）：232-234.

[11]張小紅，王偉.異維異構混沌系統同步及其在保密通信中的應用[J].計算機科學，2012，39（4）：220-222.

[12]Huang C H，Lin C H，Kuo C L.Chaos Synchronizationbased detector for power-quality disturbances classification in a power system[J].IEEE Transactions on Power Delivery，2011，26（2）：944-953.

[13]Tian L X，Xu J，Sun M.Chaos synchronization of the energy resource chaotic system with active control[J]. Int J Nonlinear Sci，2006，3（3）：228-234.

[14]Sun M，Tian L X，Xu J.Time-delayed feedback control of the energy resource chaotic system[J].Int J Nonlinear Sci，2006，3（3）：172-177.

[15]Sun M，Tian L X，Fu Y.An energy resources demandsupply system and its dynamical analysis[J].Chaos，Solitons and Fractals，2007，32：168-180.

[16]Wang Z L.Chaos synchronization of an energy resource system based on linear control[J].Nonlinear Analysis：Real World Applications，2010，11：3336-3343.

[17]高為炳.變結構控制的理論與設計方法[M].北京：科學出版社，1996.

[18]張合新，范金鎖，孟飛，等.一種新型滑模控制雙冪次趨近律[J].控制與決策，2013，28（2）：289-293.

XU Ruiping1,LIU Zhen2

1.College of Mathematics,Qingdao University,Qingdao,Shandong 266071,China
2.School of Mathematical Sciences,Ocean University of China,Qingdao,Shandong 266100,China

Synchronization problem of an energy resource chaos system is investigated.An active sliding mode controller design scheme is proposed via active control theory and sliding mode control theory.The closed loop error dynamic system depends on the parameters of the controller,therefore,the error system achieves asymptotical stability by adjusting these parameters,which means that synchronization of the energy resource chaotic system can be gained.Numerical simulation results are performed to illustrate the effectiveness and feasibility of the proposed control method.

chaos;synchronization;energy resource system;active sliding mode control

A

TP301

10.3778/j.issn.1002-8331.1306-0149

XU Ruiping,LIU Zhen.Synchronization of energy resource chaotic system using active sliding mode controller. Computer Engineering and Applications,2014,50（21）：230-233.

徐瑞萍（1976—），女，博士生，講師，研究方向：混沌系統的控制；劉振（1985—），男，博士生，研究方向：滑模變結構控制。E-mail：xuruiping1228@163.com

2013-06-17

2013-08-02

1002-8331（2014）21-0230-04

CNKI出版日期：2013-11-12，http://www.cnki.net/kcms/detail/11.2127.TP.20131112.1119.015.html