α優勢關系下粗糙集模型的屬性約簡
韋碧鵬,呂躍進,李金海
(1.柳州職業技術學院 公共基礎部,廣西 柳州 545006; 2. 廣西大學 數學與信息科學學院,廣西 南寧 530004; 3.昆明理工大學 理學院,云南 昆明 650500)
波蘭數學家Pawlak于1982年提出了粗糙集理論[1],它是一種處理模糊、不精確性以及不確定性的數學工具。近年來,由于它具有諸多優勢,已經被成功地運用于數據挖掘、模式識別、數據處理、決策分析等領域[2-4]。然而,在現實生活中,由于噪聲、測量數據的不完整性等因素,不完備信息系統依然廣泛存在。而Pawlak提出的經典粗糙集并不適用不完備信息系統。這就有必要對它進行擴充以適用于處理不完備數據。目前,針對不完備信息系統缺失值的不同理解,對經典粗糙集的擴充研究有如下模型:Kryszkiewicz[5]提出了基于容差關系的粗糙集模型,把不完備信息系統中的缺失值看作是遺漏型的,即可以和任意的對象進行比較;Stefanowski等[6]提出了基于非對稱相似關系和量化容差關系的粗糙集模型,把不完備信息系統中的缺失值看作是缺席型的;為了克服擴展模型的不足,王國胤[7]又給出了基于限制容差關系的粗糙集模型。這方面的更多研究,可以查看文獻[8-10]。
在現實世界中,很多的信息系統其屬性值域可能具有偏序性。此時,經典粗糙集方法顯得無能為力。為了能夠處理具有偏序關系的信息系統,Greco等[11]提出了基于優勢關系的粗糙集模型,即運用優勢關系代替等價關系。為了讓優勢關系下的粗糙集模型能夠同時處理缺失值,Shao等[12]把不完備序信息系統中的缺失值看作是遺漏型的,提出了基于優勢關系的不完備序信息系統,并討論了屬性約簡和規則提取。針對文獻[12]提出的優勢關系過于寬松,容易將實際不滿足條件的對象誤判為同一個優勢類,胡明禮等[13]通過引入一個閾值得到了廣義擴展優勢關系的概念,并對規則提取進行了重新考慮。此外,針對優勢系統中缺失值是缺席型的情況,楊習貝等[14]提出了相似優勢關系的粗糙集模型,并對屬性約簡做了研究。然而這并沒有彌補文獻[12]提出的優勢關系過于寬松的缺陷,并且改進后的模型還容易將一些本屬于同一決策類的對象誤判為不同決策類。這在一定程度上會影響文獻[12]提出的模型決策分析的效果。因此,Luo 等[15]進一步又給出了限制優勢粗糙集模型,既可以避免文獻[12]提出的優勢關系過于寬松的現象,又不容易將一些本屬于同一決策類的對象誤判為不同的決策類。但文獻[15]提出的限制優勢關系在某些情況下又顯得過于嚴格,例如:當2個對象在各屬性下的取值為x=(4,3,2,1),y=(*,*,2,1)時,且各屬性值域的最大值均為4,那么根據文獻[15]提出的限制優勢關系,對象x是不優于對象y的;可現實生活中,對象x優于對象y的可能性是非常大的,這有可能導致數據集中的決策規則沒有充分提取。
基于此,本文在分析不完備序信息系統中現有的幾種擴展粗糙集模型的基礎上,提出了基于α優勢關系的粗糙集模型,它既吸收了其他擴展模型的優點,又能有效克服它們的局限性,更有利于處理現實中的數據集。此外,基于α優勢關系的粗糙集模型,給出了不完備序信息系統和序決策系統的區分矩陣屬性約簡算法,并表明了其區分矩陣只能運用屬性集的冪集進行構造,而不能簡單地運用單屬性集進行構造。
1 基本概念

若存在一個屬性a∈AT使得Va為空值(記作:f(x,a)=*),則稱該信息系統是不完備的信息系統,記作:IIS;否則稱為完備的信息系統。
定義1[11]設IS=(U,AT,V,f)是一個完備信息系統,對于?A?AT,?x,y∈U,有:
?a∈A}
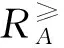
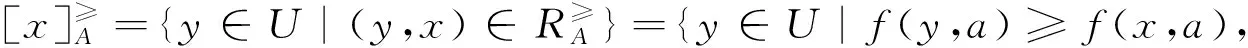

定義2[12]設IIS=(U,AT,V,f)是一個不完備信息系統,對于A?AT,?x,y∈U,有
?a∈A,f(x,a)≥
f(y,a)∨f(x,a)=*∨f(y,a)=*}
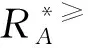
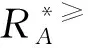

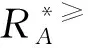
?X}
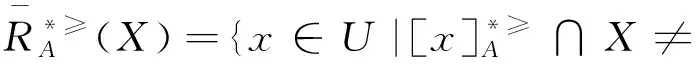
通過分析定義2,可以得出文獻[12]在不完備序信息系統中提出的優勢關系是以空值可以等于任意值為假設前提的,即認為空值可以優于任意值,同時又認為任意值可以優于空值,這顯然不符合實際情況。例如:當x=(1,1,*),y=(1,1,4),z=(*,*,4)時,其中“4”表示屬性值下最大的取值,“1”為屬性值下最小的取值。根據定義2進行分析可得:
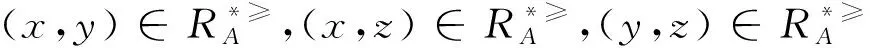
定義4[15]設IOIS=(U,AT,V,f)是一個不完備序信息系統,對于A?AT,?x,y∈U,對象在屬性集A下的限制優勢關系為
?a∈A,f(x,a)≥
f(y,a)∨(f(x,a)=maxVa∧f(y,a)=
*)∨(f(x,a)=*∧f(y,a)=minVa)}∪IU

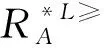
?X}
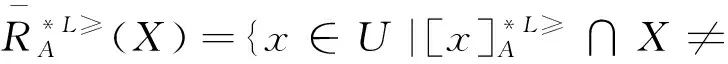
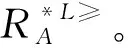
2 α優勢關系的粗糙集模型
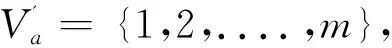
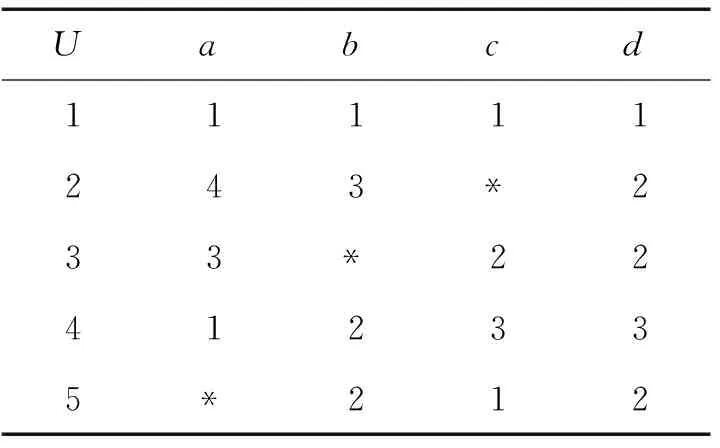
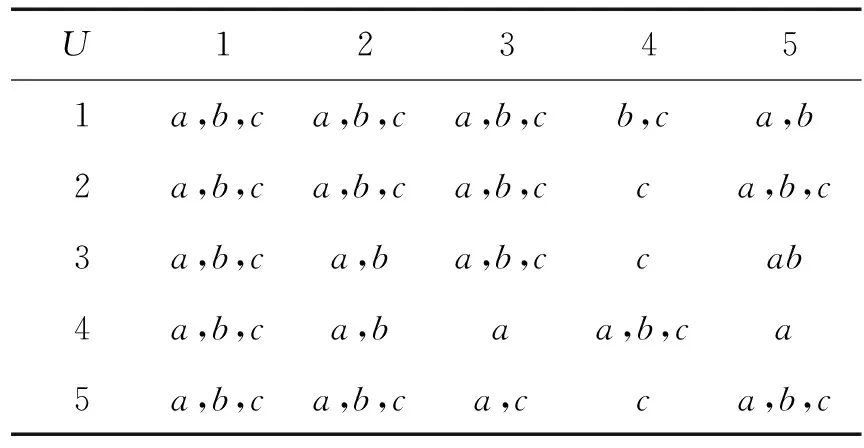
定義6 設IOIS=(U,AT,V,f)是一個不完備序信息系統,對于?a?AT,?x,y∈U,對象在屬性a下的取值為Va={a1,a2,...,am},并且a1 從定義6中得知,在單屬性下,2個對象優于的程度在0和1之間。當對象x在屬性a下取值完全小于對象y的取值時,用數值0來表示對象x劣于對象y的程度,即概率;當對象x在屬性a下取值完全大于對象y的取值時,用數值1來表示對象x優于對象y的程度。然而,當對象x和對象y有一個缺失值時,且對象在屬性下取值的多樣性,使得很難確定2個對象的優于程度;根據概率的含義,即在m個數中,有n個數優于一個確定數值的概率為n/m,得出定義6,2個對象中有一個為缺失值時它們的優于程度。當2個對象都為缺失值時,沒有根據可以判別它們之間優于程度,因此,運用1/m概率來表示,意味著優于程度很小。 定義7 設IOIS=(U,AT,V,f)是一個不完備序信息系統,對于A?AT,?x,y∈U,則對象x在屬性集A下優于y的概率為 通過定義7,可以得出不完備序信息系統各個對象的優勢類如下: 定義8 設IOIS=(U,AT,V,f)是一個不完備序信息系統,對于A?AT,?x,y∈U,有 性質1 設IOIS=(U,AT,V,f)是一個不完備序信息系統,則α優勢關系滿足如下性質: 3)當B?A?AT時,?x∈U, 性質2 設IOIS=(U,AT,V,f)是一個不完備序信息系統,對于A? 三者優勢關系滿足如下性質: ?X}= 定義10表明了基于α優勢關系的不完備序信息系統的屬性約簡保持的是對象的α優勢類不變的最小屬性組成的集合。基于此,下面給出其優勢區分矩陣構造的方法: 定義11 設IOIS=(U,AT,V,f)是一個不完備序信息系統,對于?x,y∈U,有 根據對以往知識的了解,區分矩陣的構造是可以僅僅在單元素下進行。但是,在α優勢關系的粗糙集模型中,這樣的構造是不成立的,如 假設基于α優勢關系的優勢區分矩陣可以如下構造: 在α優勢關系的不完備序信息系統中,若添加決策屬性d,則不完備序信息系統可以轉變為IODS=(U,AT∪g0gggggg,V,f)情形,其中屬性d也是一個準則,稱之為決策屬性,d?AT且*?Vd,則稱IODS為不完備序決策系統。 從定義13中可以得出,基于α優勢關系的不完備序決策系統的屬性約簡保持α優勢關系的協調性不變的最小子集。下面給出其優勢決策區分矩陣構造的方法。 定義14 設IODS=(U,AT∪g0gggggg,V,f)是一個不完備序決策系統,對于?x,y∈U,有 例1 下面給出一個不完備序決策系統,其中U={1,2,3,4,5},AT={a,b,c}為條件屬性,d為決策屬性,且對象在單個條件屬性a、b、c下最大的取值分別為4、3、3,最小值都是1。運用表1給出的不完備序決策系統來分析文獻[12]提出的優勢關系、文獻[15]提出的限制優勢關系以及本文提出的α優勢關系之間的性能;并計算α優勢關系不完備序信息系統與決策系統的屬性約簡。 表1 不完備序決策系統 1)把表1中的決策屬性去掉,不完備序決策系統轉化為不完備序信息系統,分析三者優勢關系之間的關系。 ① 根據定義2,可得文獻[12]提出的優勢關系下,各個對象的優勢類為: ③ 令α=0.6,根據定義8,可得α優勢關系下,各個對象的α優勢類為: 根據定義得出三者優勢關系下各個對象的優勢類,在文獻[12]提出的優勢關系下,對象4的優勢類為對象2、4,然而在條件屬性c下,由于對象4取得最大值,因此,對象2優于對象4的可能性是非常之小;另外,對象5的優勢類為對象2、3、4、5,然而在條件屬性a下,對象4優于對象5的可能性也是非常之小。因此,可以說文獻[12]提出的優勢關系劃分的粒度過大了。在文獻[15]提出的限制優勢關系下,對象3的優勢類為對象3,然而對象2優于對象3的可能性是非常之大。因此,說明了文獻[15]提出的限制優勢關系劃分的粒度過細了。然而,在α優勢關系下,設定確定的α取值,各個對象的優勢類就不會出現上述的情況;可以看出,α優勢關系吸取了上述兩者優勢關系的優點,丟棄了兩者的缺陷,更加符合實際情況,更有利于去處理現實生活中存在復雜的不完備序信息系統。 2)不完備序信息系統的屬性約簡 根據定義11,結合α優勢類,可以得出不完備序信息系統的優勢區分矩陣如表2。 表2 優勢區分矩陣 故Δ*≥=(a∨b∨c)∧(a∨b)∧a∧c∧(a∨c)∧(a∧b)∧(b∨c)=abc,即該不完備序信息系統的屬性約簡為abc。 3)不完備序決策系統的屬性約簡。 由于各個對象在決策屬性下的優勢類如下: 根據定義14,可以得出不完備序決策系統的優勢決策區分矩陣如表3。 表3 優勢決策區分矩陣 由于現實中處理的數據很多是不完備的,且存在偏序性,因此研究處理這種復雜數據情況的粗糙集方法是很有實際意義的。本文通過對現有優勢關系的分析后提出了α優勢關系及其相應的粗糙集模型,以使得對不完備序信息系統的數據分析更加合理。此外,在基于α優勢關系的粗糙集模型上,給出了不完備序信息系統的優勢區分矩陣以及不完備序決策系統的優勢決策區分矩陣,從而實現了屬性約簡,同時也表明了區分矩陣只能運用屬性集的冪集進行構造,而不能運用單個屬性集進行構造。 需要指出的是,在α優勢關系的基礎上,還可以進一步研究不協調不完備序決策系統的屬性約簡算法,這是本文的下一步工作任務。 參考文獻: [1]PAWLAK Z. Rough sets [J]. International Journal of Computer and Information Sciences, 1982, 11(5): 341-356. [2]張文修,吳偉志,梁吉業,等.粗糙集理論與方法[M].北京:科學出版社, 2001: 14-19. [3]李金海,呂躍進.決策系統的快速屬性約簡算法[J].電子科技大學學報, 2007, 36(6): 1237-1240. LI Jinhai, Lü Yuejin. Quick attribute reduction algorithm on decision system[J]. Journal of University of Electronic Science and Technology of China, 2007, 36(6): 1237-1240. [4]覃麗珍,姚炳學,李金海.基于信息量的完備覆蓋約簡算法[J]. 計算機科學, 2012, 39(10): 235-239. QIN Lizhen, YAO Bingxue, LI Jinhai. Complete algorithm for covering reduction based on information quantity[J]. Computer science, 2012, 39(10): 235-239. [5]KRYSZKIEWICZ M. Rough set approach to incomplete information systems [J]. Information Sciences, 1998, 112: 39-49. [6]STEFANOWSKI J, TSOUKIAS A. On the extension of rough sets under incomplete information[C]//Proceedings of New Directions in Rough Sets, Data Mining and Granular-Soft Computing. Berlin: Springer, 1999: 73-81. [7]王國胤. Rough集理論在不完備信息系統中的擴充[J]. 計算機研究與發展, 2002, 39 (10): 1238-1243. WANG Guoyin. Extension of rough set under incomplete information systems[J]. Journal of Computer Research and Development, 2002, 39 (10): 1238-1243. [8]LIANG J Y, QU K S. Information measures of roughness of knowledge and rough sets in incomplete information systems[J]. Journal of System Science and System Engineering, 2001, 24(5): 544-547. [9]GRZYMALA-BUSSE J W. Characteristic relations for incomplete data: a generalization of indiscernibility relation[C]//Proceedings of Rough Sets and Current Trends in Computing. Berlin: Springer, 2004: 244-253. [10]楊習貝, 楊靜宇, 吳陳, 等. 不完備信息系統中的集對分析方法[J]. 計算機科學, 2007, 34(4): 171-174. YANG Xibei, YANG Jingyu, WU Chen, et al. Set pair analysis in incomplete information systems[J]. Information Science, 2007, 34(4): 171-174. [11]GRECO S, MATARAZZO B, SLOWINGSKI R. Rough sets theory for multicriteria decision analysis[J]. European Journal of Operational Research, 2001, 129(1): 1-47. [12]SHAO M W, ZHANG W X. Dominance relation and rules in an incomplete ordered information system [J]. International Journal of Intelligent Systems, 2005, 20: 13-27. [13]胡明禮, 劉思峰. 基于廣義擴展優勢關系的粗糙決策分析方法[J]. 控制與決策, 2007, 22(12): 1347-1351. HU Mingli, LIU Sifeng. Rough analysis method of multi-attribute decision making based on generalized extended dominance relation[J]. Control and Decision, 2007, 22(12): 1347-1351. [14]YANG X B, YANG J Y, WU C, et al. Dominance-based rough set approach and knowledge reductions in incomplete ordered information system[J]. Information Sciences, 2008, 178: 1219-1234. [15]LUO G Z, YANG X B. Limited dominance-based rough set model and knowledge reductions in incomplete decision system[J]. Journal of Information Science and Engineering, 2010, 26: 2199-2211.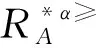

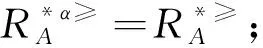
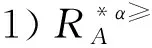
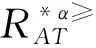

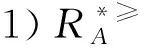
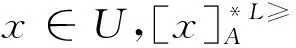
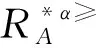

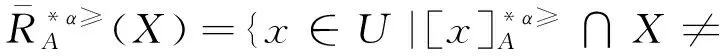
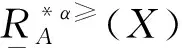

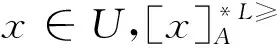
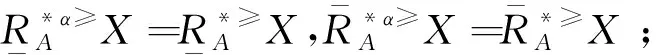
3 基于α優勢關系粗糙集模型的屬性約簡
3.1 不完備序信息系統的屬性約簡

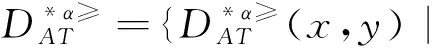
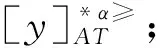

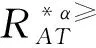
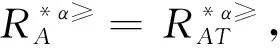
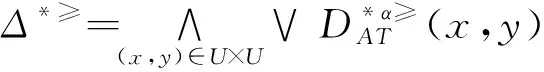
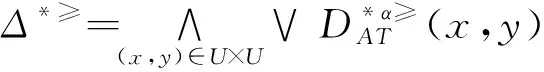
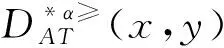
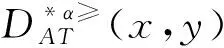
3.2 不完備序決策系統的屬性約簡
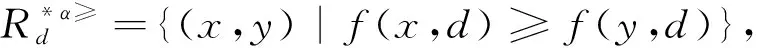
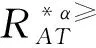
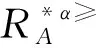
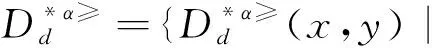
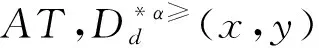
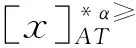
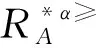
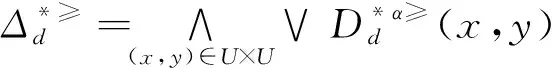
4 實例分析
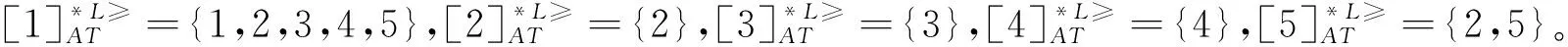
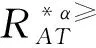

5 結束語

