基于覆蓋粗糙集的語言動力系統
湯建國,汪江樺,韓莉英,祝峰
(1.新疆財經大學 計算機科學與工程學院,新疆 烏魯木齊 830012; 2. 閩南師范大學 粒計算實驗室,福建 漳州 363000)
語言動力系統(linguistic dynamic systems, LDS)的概念是王飛躍教授在20世紀90年代初提出的,它是以詞計算為基礎來對問題進行動態描述、分析、綜合,進而設計、控制和評估的系統[1- 2]。由于語言具有很強的不確定性,其語義會隨著語境及語調等因素的不同而發生改變,因而如何處理這種不確定性是LDS研究中的一個關鍵問題。王飛躍教授在這方面做了大量基礎性工作[3-6],他利用模糊數學的方法來解決不確定問題,建立了基于模糊邏輯的LDS模型。
近年來,粗糙集[7-8]作為一種處理不確定問題的有效方法得到了快速發展,其擴展理論覆蓋粗糙集[9-16]也引起很多學者的關注和研究興趣,涌現出許多重要的研究成果[17-24]。本文將利用覆蓋粗糙集方法來研究語言動力系統中的不確定問題,建立基于覆蓋粗糙集的LDS模型,利用粗糙集中的上下近似思想探討解決實際問題的推理方法,并通過實例對其具體的應用和計算方法進行闡述。
1 相關定義
為了討論方便,在本文的后續內容中,令U表示一個非空有限集合,稱為論域。
1.1 覆蓋粗糙集
設U是一個論域,C是U的一個子集族。如果C中的所有子集都不空,且∪C=U,則稱C是U的一個覆蓋;稱有序對(U,C)為覆蓋近似空間。對于任意一個子集X?U,定義X關于C的下近似和上近似分別為:
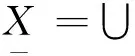
{K∈C|K?X}
(1)
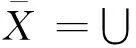
(2)
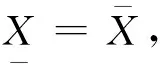
C*(X) = {K∈C|K?X}
(3)
C*(X) = {K∈C|K∩X≠}
(4)
在粗糙集中,一個集合的下近似中的元素被認為是確定屬于該集合的,而上近似中的元素則被認為是可能屬于該集合的。因此,可以根據下近似來獲取確定的規則和知識,而依據上近似來獲取可能性的規則和知識。由于C*(X) ?C*(X),所以在C*(X)中除去C*(X)后剩余的集合都是可能屬于集合X的。令C**(X)表示C*(X)與C*(X)的差集,即:
C**(X) =C*(X) -C*(X)
(5)
對于U中的任意一個元素x,其關于C的鄰域為
N(x) = ∩{K∈C:x∈K}
(6)
1.2 語言動力系統
語言動力系統是一類特殊的動力學系統,它將問題(過程)、情形(狀態)、策略(控制器)、觀察(反饋)、目標和評估用文字術語來表達[2]。王飛躍教授結合詞計算將LDS建模成一個模糊動力學系統,其狀態方程、輸出方程和反饋控制分別表示如下:
狀態方程:Xk+1=F(Xk,Uk,k),F:In×Im×Z+→In。
輸出方程:Yk=H(Xk,k),H:In×Z+→Ip。
反饋控制:Uk=R(Yk,Vk,k),R:Ip×Iq×Z+→Im。
式中:Z+= {0, 1,…,K},Xk∈In是一個表示系統狀態的向量,Yk∈Ip是輸出,Vk∈Iq是輸入,Uk∈Im是控制,k是離散時間實例,F,H,R是模糊邏輯算子,它們各自定義了LDS中的系統、輸出和控制映射。系統中變量X、Y、U和V的定義域分別為:
DX= {x1,x2, …,xn}
DY= {y1,y2, …,yp}
DU= {u1,u2, …,um}
DV= {v1,v2, …,vq}
2 問題的提出
語言動力系統是一個非常復雜的動力學系統,它面向的處理對象是自然語言所表達的人類知識,而這種知識具有很強的不確定性。因而,如何有效應對這種不確定性是語言動力系統研究中的一個關鍵的問題。
王飛躍教授利用基于模糊邏輯的詞計算對LDS進行建模,來處理LDS中的不確定問題。詞計算是以隸屬函數為基礎的一種計算理論,它可以在一定程度上很好地反映和處理自然語言中的不確定性。但由于如何確定隸屬函數是一件繁瑣而困難的工作,因而在面對復雜的大數據問題時,這種方法就顯得力不從心。
粗糙集是一種重要的處理不確定問題的理論,與詞計算不同的是,粗糙集在解決問題時不依賴給定數據之外的任何先驗知識,而是完全根據所給數據來客觀地獲取知識。因此,利用粗糙集分析和處理數據時不需去確定隸屬函數。經典的粗糙集理論是建立在對論域劃分的基礎上,即不同概念之間不存在交集。而在現實世界中,用自然語言描述的概念往往具有一定的模糊性,如很難對“年輕”這一概念予以確切地描述和區分,這就會將“年輕”中的一些人也分到諸如“較年輕”或“較不年輕”等概念中去,反之亦然。鑒于此,Zakowski[9]將經典粗糙集擴展為了覆蓋粗糙集,從而允許不同概念之間可以存在非空交集,增強了粗糙集對實際問題的處理能力。
覆蓋的這一特征與自然語言表達知識的特點非常相似,即在對概念的表述上都存在一定的不確定性,這就使得利用覆蓋粗糙集來研究語言動力系統具有很強的可行性。目前,覆蓋粗糙集研究已取得長足發展,在諸如公理化和模型擴展等理論方面和數據挖掘等應用方面都取得了很多成果,已成為一種重要的研究不確定問題的方法。因此,基于上述分析,本文將利用覆蓋粗糙集對語言動力系統中的不確定問題展開探索性的研究。
3 覆蓋粗糙集的LDS模型
3.1 模型
自然語言的豐富內涵造成了語言表達知識的不確定性,如何用計算機準確地判斷一句話所要表示的意義,對計算機科學來說無疑是一個巨大的挑戰。覆蓋粗糙集通過上、下近似逼近的方式來近似地刻畫目標集合,可以快速地給目標集合的不確定性劃定一范圍,提高了知識獲取的效率。這一思想為處理不確定問題提供了一個很好的方法,借助這種思想建立了基于覆蓋粗糙集的LDS模型:
狀態方程:
輸出方程:
反饋控制:
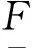
3.2 推理方法
在覆蓋粗糙集理論中,認為目標集合的下近似集是確定成立的知識,而上近似集則是可能成立的知識。根據這一特點,設計了基于覆蓋粗糙集的LDS分析和解決問題的推理過程,其主要步驟為:
1) 將語言描述的背景知識轉換為覆蓋形式的知識。粗糙集中認為知識是一種分類能力,并將每類事物都用一個集合來表示。在覆蓋粗糙集中,這些類對應的集合被稱為覆蓋塊。于是,為了求解問題需要先將已有的知識轉換為反映分類能力的覆蓋。具體來說,首先要依據實際問題來獲得論域U,其次再根據已有知識得到覆蓋C,最后為了實現用自然語言來描述計算結果,需要給予覆蓋中的每個覆蓋塊一個語言標簽ω。
①根據實際情況確定論域U;
②根據對問題的已有知識來獲得U上的覆蓋C= {K1,K2, …,Kn};
③根據問題的具體情況給各覆蓋塊添加語言標簽 →ω(C) = {ω1,ω2, …,ωn},其中,?Ki∈C,ω(Ki) =ωi。
2) 將要求解的問題轉換成目標集合。通過分析問題的特點,將問題轉換為目標集合X。
3) 根據得到的覆蓋和式(3)、(4)求得目標集合X的C*(X)和C*(X)。
4) 根據C*(X)和C*(X)來得出確定成立和可能成立的知識。在這一過程中,一方面要根據問題給出描述結論的2種語言范式,即描述確定成立知識和描述可能成立知識的語言范式。另一方面,需要結合1)中的ω(C)來實現計算結果的語言表示。
此外,在實際問題中經常會遇到以一個數值區間表示的集合,本文對于這類集合的一些基本運算和相互間的關系做出如下規定:
設a、b、c和d是4個任意實數,其中a≤b,c≤d,A= [a,b]和B= [c,d]是2個數值區間。定義A和B的交運算、并運算以及子集等關系如下:
1)A∩B。
若a≥c且b≤d,則A∩B= [a,b];
若c≤a≤d且b>d,則A∩B= [a,d];
若a≤c且c≤b≤d,則A∩B= [c,b];
若a≤c且b>d,則A∩B= [c,d];
若b
2)A∪B。
若a≥c且b≤d,則A∪B= [c,d];
若c≤a且b>d,則A∪B= [c,b];
若a≤c且b≤d,則A∪B= [a,d];
若a≤c且b>d,則A∪B= [a,b]。
3)A?B。
若c≤a且b≤d,則稱A是B的子集,記為A?B。
4)A∈B。
若a=b且A?B,則稱A屬于B,記為A∈B。
5)A=B
若a=c且b=d,則稱A等于B,記為A=B。
4 實例與分析
例1 將學生的成績分為優、良、中、差4個等級,對應的分值區間分別為(85, 100]、(75, 90)、(65, 80)、[0, 70)。假設學生小明的成績等級為“中”,分析哪些成績等級的學生成績比小明的成績好。
按照前面給出的推理過程,依次展開如下4個推理步驟:
1)根據已知條件可知學生的成績分數范圍為[0, 100],即:論域U= [0, 100];
其次,將各成績等級作為不同的類別,從而得到U上的覆蓋C= {K1,K2,K3,K4} = {(85, 100], (75, 90), (65, 80), [0, 70)};
最后,對覆蓋C中的各覆蓋塊添加語言標簽。從例題中可知,C中的4個覆蓋塊分別對應成績等級中的優、良、中、差,于是可得:
ω(C) = {優, 良, 中, 差},其中,ω(K1) = 優,ω(K2) = 良,ω(K3) = 中,ω(K4) = 差。
2)由于小明的成績等級為“中”,其對應的成績為(65, 80),也就是說小明的具體成績可以是這個區間中的任何一個實數。若令小明的成績為a(65
3)根據得到的C和X可知,在C中只有覆蓋塊K= (85, 100] ?X,其余覆蓋塊均不是X的子集。根據式(3)可得
C*(X) = {K1}
類似地,K1∩X= (85, 100] ≠ ?,K2∩X= (80, 90] ≠ ?。根據式(4)可得
C*(X) = {K1,K2}
進一步地,根據式(5)可得:C**(X) = {K2}。
4)給出描述結論的2種語言范式。
① 確定成立知識的語言范式。
“成績等級為“ω(K)”的學生成績“一定”比小明的成績好。”這里K∈C*(X)。
② 可能成立知識的語言范式。
“成績等級為“ω(K)”的學生成績“可能”比小明的成績好。”這里K∈C**(X)。
其次,結合ω(C)來實現計算結果的語言表示。
由C*(X) = {K1}且ω(K1) =“優”可得
“成績等級為“優”的學生成績“一定”比小明的成績好。”
再由C**(X) = {K2}且ω(K1) =“良”可得
“成績等級為“良”的學生成績“可能”比小明的成績好。”
這說明如果一個學生的成績等級是“優”,則他她的成績一定比小明要好。如果一個學生的成績等級為“良”,則他的實際成績也有可能比小明好。由此可見,這種方法判斷結果與在現實中的理解和分析是一致的。
上例通過對一個用自然語言描述的問題進行推理后得出了用自然語言描述的結果,下面再通過一個例子來從另一個角度展示如何對一個非自然語言問題進行推理。
例2 假設在例1中,小明的期中和期末考試成績分別是76分和83分。請對小明的這2次成績進行等級評價。
先對小明的期中成績進行評價。由于論域U、覆蓋C以及ω(C)都與例1相同,只需確定本例中的目標集合X。小明的成績是76分,可將此成績看成是區間[76, 76]。由于單個分值不具代表性,以該分值的所在的鄰域作為目標集合。根據式(6)可得:
N(76) = ∩{K2,K3} = (75, 80)
即目標集合為X= (75, 80)。從而根據式(3)和(4)可得
C*(X) = ?,C*(X) = {K2,K3}
由于C*(X)為空,所以在本例的問題中不存在確定成立的結論,而只有可能成立的結論。
可能成立知識的語言范式:
“小明的成績等級“可能”為“ω(K)””。
結合ω(C)可得
“小明的成績等級‘可能’為‘中’”。
“小明的成績等級‘可能’為‘良’”。
同理,在分析小明的期末成績時,可以得到對應于83分的鄰域為區間(75, 90),即目標集合X= (75, 90)。從而根據式(3)和(4)可得
C*(X) = {K2},C*(X) = {K2}
進一步地,根據式(5)可得:C**(X) = ?。
從而可得小明期末成績等級評價的結果為:“小明的成績等級“一定”為“良””。
上例對一個具體成績的等級進行了推理和描述,其結果大體與在現實中的判斷結果一致。之所以說大體上一致是因為在現實中,用“中”或“良”來描述小明的成績還是顯得有些寬泛,通常根據經驗或感覺將其更細致地表述為諸如“中上”或“良下”等。在現實生活中,人們的這種“經驗”和“感覺”在描述事物和表達信息時往往非常微妙,雖然其傳遞的是一種模糊的信息,但卻并不讓人感到費解。相反,人們多數會更愿意接受這種描述。
那么在推理方法中,如何反映和實現自然語言中類似人的這種“經驗”和“感覺”呢?其實已有的很多方法都可以用來解決這個問題,比如概率的方法、模糊集中的隸屬度方法以及粗糙集中的描述距離的熵等。但由于自然語言本身是靈活多變的,相同的一句話在不同場景或時間背景下意義會存在很大不同,所以在用這些方法解決這個問題是,還需要采取具體問題具體對待的方式來靈活處理。在后續的研究中,將對這一問題展開深入的分析和研究。
5 結束語
本文利用覆蓋粗糙集的方法對語言動力系統進行建模,提出了分析和解決問題的推理方法,通過實例對其進行了闡述和驗證,結果表明模型計算得出的結論與現實中的實際情況基本一致。在后續研究中,將對人在用自然語言描述事物時的模糊性修飾和表述進行研究,以使模型的計算結果更加準確合理。
參考文獻:
[1]WANG Feiyue. Modeling, analysis and synthesis of linguistic dynamic systems: a computational theory[C]//IEEE International Workshop on Architecture for Semiotic Modeling and Situation Control in Large Complex Systems. Monterey, CA, 1995: 173-178.
[2]王飛躍. 詞計算和語言動力學系統的計算理論框架[J]. 模式識別與人工智能, 2001, 14(4): 377-384.
WANG Feiyue. Computing with words and a framework for computational linguistic dynamic systems[J]. Pattern Recognition and Artificial Intelligence, 2001, 14(4): 377-384.
[3]WANG F Y. On the abstraction of conventional dynamic systems: from numerical analysis to linguistic analysis[J]. Information Sciences, 2005, 171(1/2/3): 233-259.
[4]WANG F Y, YANG T , MO H. On fixed points of linguistic dynamic systems[J]. Journal of System Simulation, 2002, 14(11): 1479-1485.
[5]王飛躍. 詞計算和語言動力學系統的基本問題和研究[J]. 自動化學報, 2005(6): 32-40.
WANG Feiyue. Fundamental issues in research of computing with words and linguistic dynamic systems[J]. Acta Automatica Sinica, 2005(6): 32-40.
[6]莫紅,王飛躍. 基于詞計算的語言動力系統及其穩定性[J]. 中國科學: F輯, 2009, 39(2): 254-268.
[7]PAWLAK Z. Rough sets[J]. International Journal of Computer and Information Sciences, 1982, 11(5): 341-356.
[8]PAWLAK Z. Rough Sets: Theoretical aspects of reasoning about data[M]. Boston: Kluwer Academic Publishers, 1991: 1-79.
[9]ZAKOWSKI W. Approximations in the space(U,∏)[J]. Demonstratio Mathematica, 1983(16): 761-769.
[10]ZHU W, WANG F. Reduction and axiomization of covering generalized rough sets[J]. Information Sciences, 2003, 152: 217-230.
[11]ZHU W, WANG F. Axiomatic systems of generalized rough sets[C]//Proceedings of the 1st International Conference on Rough Sets and Knowledge Technology. Chongqing, China, 2006: 216-221.
[12]ZHU W, WANG F. Covering based granular computing for conflict analysis[C]//IEEE International Conference on Intelligence and Security Informatics. San Diego, CA, USA: 2006: 566-571.
[13]ZHU W, WANG F. Relationships among three types of covering rough sets[C]//IEEE International Conference on Granular Computing. Atlanta, GA, USA, 2006: 43-48.
[14]ZHU W, WANG F. Topological properties in covering-based rough sets[C]//Proceedings of the 4th International Conference on Fuzzy Systems and Knowledge Discovery. Haikou, China, 2007: 289-293.
[15]ZHU W, WANG F. On three types of covering-based rough sets[J]. IEEE Transactions on Knowledge and Data Engineering, 2007, 19(8): 1131-1143.
[16]ZHU W, WANG F. The fourth type of covering-based rough sets[J]. Information Sciences, 2012, 201: 80-92.
[17]YAO Y Y, YAO B X. Covering based rough set approximations[J]. Information Sciences, 2012, 200: 91-107.
[18]GE X, BAI X L, YUN Z Q. Topological characterizations of covering for special covering-based upper approximation operators[J]. Information Sciences, 2012, 204: 70-81.
[19]WANG L J , YANG X B, YANG J Y, et al. Relationships among generalized rough sets in six coverings and pure reflexive neighborhood system[J]. Information Sciences, 2012, 207(10): 66-78.
[20]TANG J G, SHE K, WANG Y Q. Covering-based soft rough sets[J]. Journal of Electronic Science and Technology, 2011, 9(2): 118-123.
[21]TANG J G, SHE K, ZHU W. The refinement in covering-based rough sets[C]//Proceedings of the International Conference on Granular Computing. Taipei, China, 2011: 641-646.
[22]TANG J G, SHE K, ZHU W. Covering-based rough sets based on the refinement of covering-element[J]. International Journal of Computational and Mathematical Sciences, 2011, 5: 198-208.
[23]WANG S P, ZHU W. Matroidal structure of covering-based rough sets through the upper approximation number[J]. International Journal of Granular Computing, Rough Sets and Intelligent Systems, 2011, 2(2): 141-148.
[24]ZHANG Y, LI J, WU W. On axiomatic characterizations of three pairs of covering based approximation operators[J]. Information Sciences, 2010, 180(2): 274-287.

