(T, S)-凸直覺模糊集

劉自新，王 森

（大連大學 信息工程學院，遼寧 大連 116622）

0 引言

三角范數是取值于[0,1]上的二元函數，它首先是由Menger于1942年在研究統計問題時提出的[1]，20世紀60年代，Schweizer和Sklar在研究概率度量空間時也涉及到三角范數和三角余范數的概念[2,3]，1998年E.P.Klement和R.Mesiar對三角范數的概念進行了新的闡述，并對其作了較系統的研究[4]。三角范數理論在概率論、決策論、統計學、博弈論、函數方程等領域都有著重要的應用價值[5-6]。

模糊集和凸模糊集的概念是1965年由L A Zadeh首先提出來的[7]，其后一些學者在Zadeh定義的基礎上進行了擴展研究，1971年 Rosenfeld[8]提出了模糊群的概念，1979年Anthony和Sherwood[9]用T-范數對模糊群重新進行了定義，此后眾多學者又據此得到了模糊子群的若干性質。1977年 Katsaras和 Liu[10]提出了向量空間的模糊子空間的概念。文獻[11]中用T-范數推廣了凸模糊集和模糊子空間的研究成果。1986年K.Atanassov[12]在模糊集定義的基礎上，提出了直覺模糊集的概念，許多學者對直覺模糊集的理論和應用進行了大量的研究，使直覺模糊集理論得到了快速的發展。文獻[13,14]中提出了直覺模糊子空間和直覺模糊仿射空間的概念，并對有關性質進行了討論。本文將文獻[13,14]中所用的算子進行了推廣，用T -范數和S-范數給出了凸直覺模糊集和直覺模糊子空間、直覺模糊仿射集的定義，并討論了它們之間的關系，所以本文也是對文獻[13-14]的繼續深入和推廣。

1 預備知識

設 ?a,b,c,d∈[0,1]， 如 果 映 射T:[0,1]×[0,1]→ [0,1]， 滿 足 條 件(1)T(a,b) =T(b,a)；(2)T(T(a,b),c) =T(a,T(b,c))；(3)a≤c,b≤d?T(a,b) ≤T(c,d)； (4)T( 1,a) =a，則稱T為T-范數。如果映射S:[0,1]×[0,1]→ [0,1]， 滿 足 條 件(1)S(a,b) =S(b,a)；(2)S(S(a,b),c) =S(a,S(b,c))；(3)a≤c,b≤d?S(a,b) ≤S(c,d)； (4)S(a, 0)=a，則稱S為T-余范數,或稱為S-范數。顯然，min{a,b}為最大的T-范數，而max{a,b}為最小的S -范數。設N: [0,1]→ [0,1]且對任意a∈[0,1]，N(a) = 1 ?a，則稱N 為[0,1]上的偽補。在偽補的定義下，如果已知一個T-范數，容易證明S(a,b) = 1 ?T( 1 ?a, 1?b為S-范數，而如果已知一個S-范數，則T(a,b) = 1 ?S( 1 ?a, 1 ?b)為T-范數，稱此時的S -范數和T-范數為對偶范數。

集合A= {(x, μA(x) )|x∈X}稱為論域X上的一個模糊子集[7]，其中μA( ·):X→[0,1]稱為模糊子集A 的隸屬函數，在不致誤解的情況下，模糊子集A和它的隸屬函數μA(x)將不加區分，同時模糊子集也常簡稱為模糊集。對任意λ∈[0,1]，x,y∈X，如果 μA(λx+ ( 1 ? λ )y) ≥ min{μA(x) ,μA(y)}，則稱A 為 凸 模 糊 集 ； 如 果μA(λx+ (1 ?λ)y) ≤ max{μA(x) ,μA(y)}，則稱A 為凹模糊集。設*表示一個T-范數，模糊集μ:Rn→[0,1]稱為*-凸模糊集[11]，如果對任意x,y∈Rn，λ∈[0,1]，都有μ(λx+ ( 1 ?λ)y) ≥μ(x) *μ(y)，稱A=(X,μA,νA)為X 上的一個直覺模糊集[12]，如果μA:X→[0,1]，νA:X→[0,1]為兩個映射且μA(x) +νA(x) ≤ 1，?x∈X。為簡便，記直覺模糊集A=(μA,νA)。論域X上的所有直覺模糊集記為IF(X)。設A∈IF(X)，若至少存在一點x∈X，使得μA(x) = 1，νA(x) = 0，則稱A為正規的直覺模糊集。設A=(μA,νA)，如果μA為X上的凸模糊集且vA為X 上的凹模糊集，則稱A 為X上的凸直覺模糊集[15]。

2 (T, S )-凸直覺模糊集

定義2.1

設A= (μA,νA)∈IF(X)，T,S為對偶范數，若對?x,y∈Rn，t∈[0,1]，都有

則稱A 為(T,S)-凸直覺模糊集。

特別地，如果S=∨，T=∧，則稱A 為(∧,∨)-凸直覺模糊集。

顯然，(∧,∨)-凸直覺模糊集一定是(T,S)-凸直覺模糊集。

R 上每個正規的(T,S)-凸直覺模糊集都是(∧,∨)-凸直覺模糊集。

定理2.1

對兩個(T,S)-凸直覺模糊集A,B，定義(T(μA,μB) ,S(νA,νB))為:

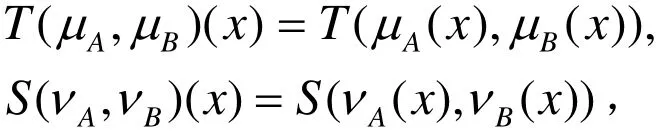
證明：

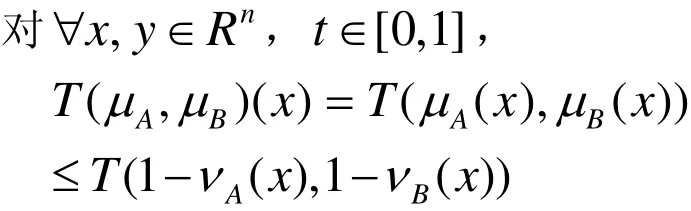
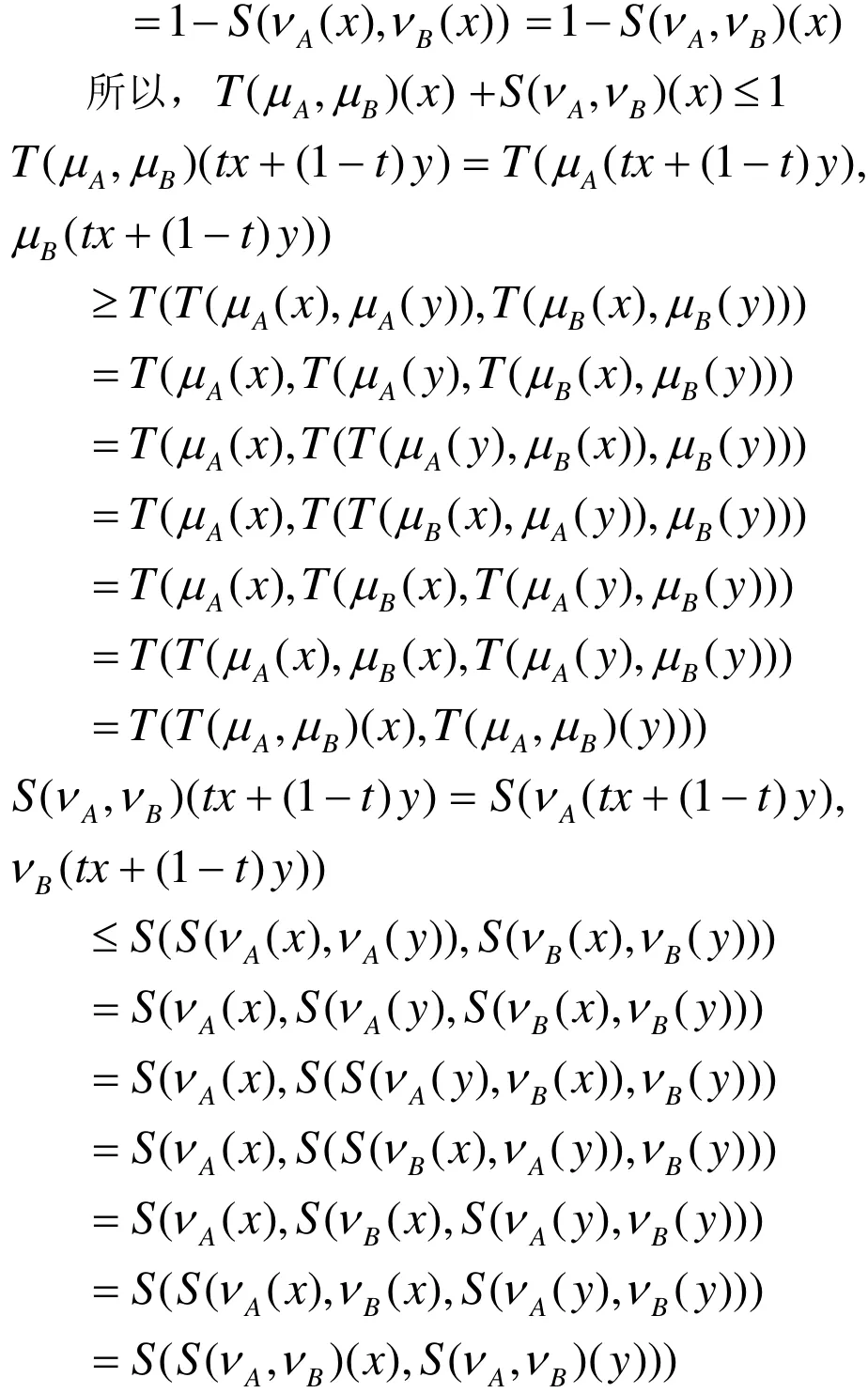
假設(μi,νi)，1≤i≤n是R 上(T,S)-凸直覺模糊 集 序 列 ，(x1,… ,xn)∈Rn， 定 義(λ,μ) :Rn→ [0 ,1]×[0,1]為

定理2.2

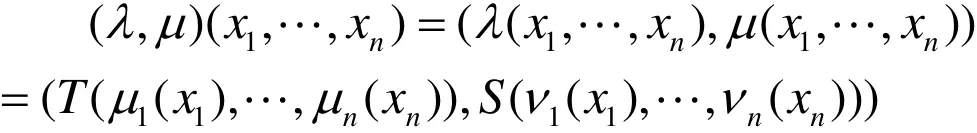
則(λ,μ)為Rn上的(T,S)-凸直覺模糊集。

證明：由定理2.1及數學歸納法可證。

定理2.3

(T,S)-凸直覺模糊集。

證明：

設(x, y) ∈ Rn，t∈[0,1]。對所有i∈ I，都有

即(∧iμi∈I, ∨i∈Iνi)為(T,S)-凸直覺模糊集。

定理2.4

假設A 是一個(T,S)-凸直覺模糊集，為非負實數有限序列且，則

證明：

當r=1和r=2時，結論顯然成立。

假設r = k時不等式成立。

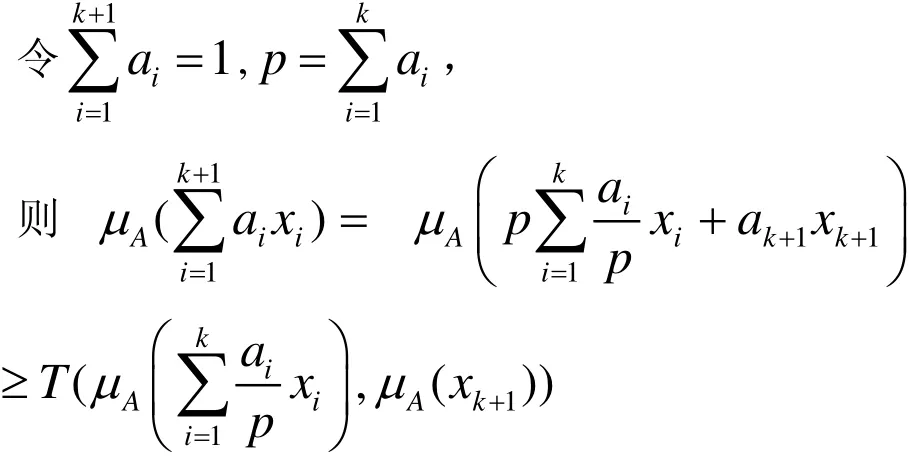
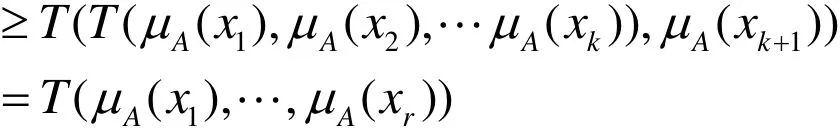
即r=k+1時不等式也成立。

3 (T, S )-直覺模糊子空間

定義3.1

Rn上的一個直覺模糊集A 稱為(T,S)-直覺模糊子空間，如果對?x,y∈Rn，?a,b∈R，有

定理3.1

x∈ Rn

(2)μA(ax) = μA(x) ,νA(ax) = νA(x)，a為非零實數，

(3)A為(T,S)-凸直覺模糊集，

則A 為(T,S)-直覺模糊子空間。

如果A為正規的直覺模糊集，則定理的必要性成立。

如果一個直覺模糊集A滿足下面的條件：

證明：

設直覺模糊集A滿足條件(1)～(3)。

令x,y∈Rn，a, b ∈ R+，則

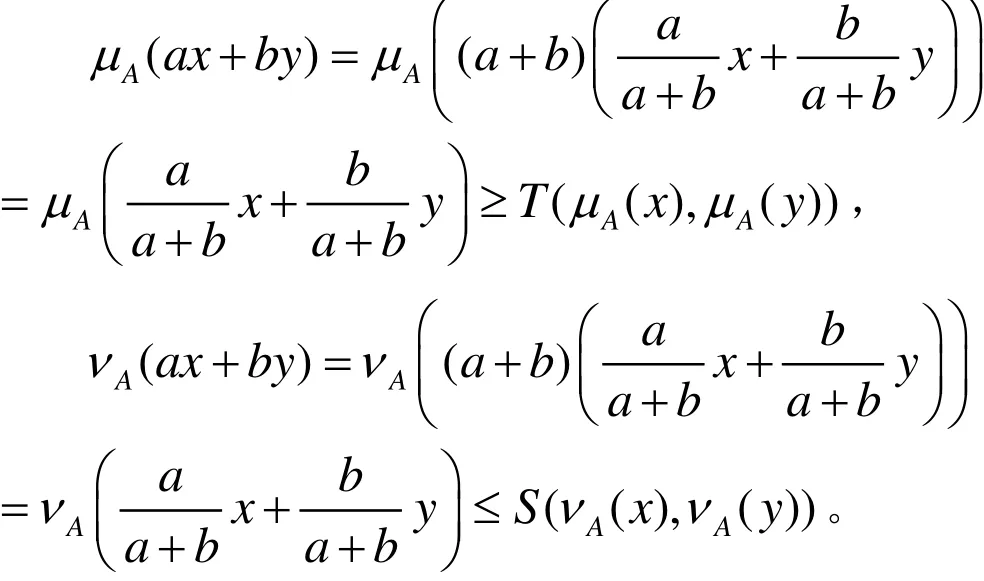
因 為 對x∈Rn， 有 μ(?x) = μ(x),

A

A νA(?x) = νA(x)，所以上述不等式在a,b∈R?時也成立。

同樣，當a· b＜0時也成立。

如果a=b=0，我們有

因此A 是(T,S)-直覺模糊子空間。

如果A 為正規的直覺模糊集，則存在y' ∈Rn，有μA(y')=1,νA(y') = 0。

條件3是顯然的。

在(T,S)-直覺模糊子空間的定義中，令b= 0 ,y=y'，有

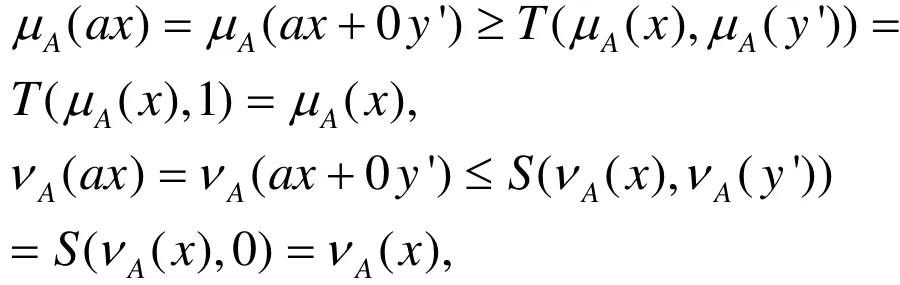
顯然，對所有x∈Rn，非零實數a有

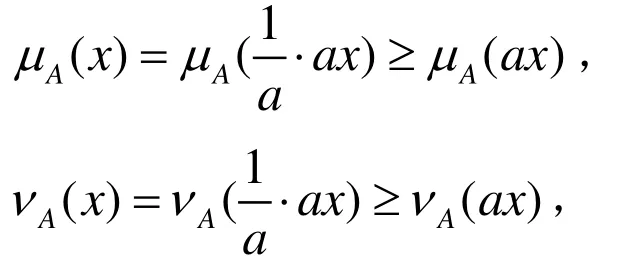
從而條件2成立。

令a=b= 0 ,y=y'，則對任意x，

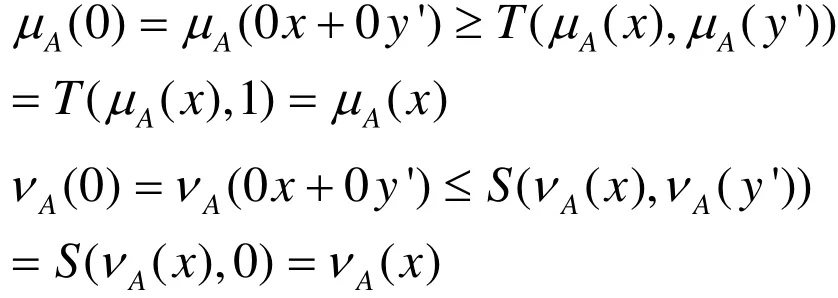
由此可得，μA(0)=1,νA( 0) = 0，故條件1成立。

定義3.2

設z∈Rn,z + A表示直覺模糊集A的平移，對任意x∈Rn，定義

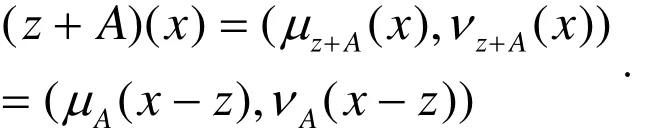
定義3.3

設A 為直覺模糊集，如果對?x,y∈Rn，t∈R,都有

則稱A 為一個(T,S)-直覺模糊仿射集。

定理3.2

(1)如果A 為(T,S)-直覺模糊子空間，則其平移是(T,S)-直覺模糊仿射集。

(2)每個正規的(T,S)-直覺模糊仿射集的平移是一個(T,S)-直覺模糊子空間。

證明:

(1)設A 為(T,S)-直覺模糊子空間，則對?x,y∈Rn，z0∈Rn,t∈R，

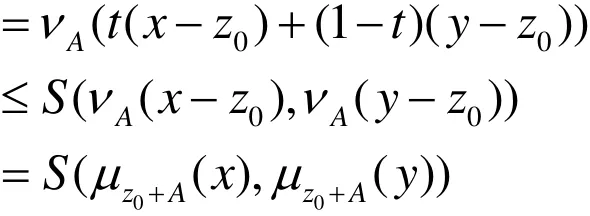
由定義3.3知，A為(T,S)-直覺模糊仿射集。

(2)設A 為Rn上的正規的直覺模糊仿射集，則存在y' ∈Rn，使μA(y')=1,νA(y') = 0。

對任意x∈Rn，定義B= ?y' +A。設a為非零實數，則

由此可推得μB(ax) = μB(x)，νB(ax) = νB(x)。

由(1)知，B 是(T,S)-凸直覺模糊集。再由定理3.1知，B 是(T,S)-直覺模糊子空間。

4 結論

本文用T -范數和S -范數定義了(T,S)-凸直覺模糊集，(T,S)-直覺模糊子空間和(T,S)-直覺模糊仿射集，并討論了(T,S)-凸直覺模糊集的一些性質，(T,S)-直覺模糊子空間和(T,S)-直覺模糊仿射集之間的關系。這些結果是對文獻[13,14]的繼續深入和推廣。

[1]K Menger. Statistical metrics[J]. Proc. Natl. Acad. Sci., USA,1942, 8: 535-537.

[2]B Schweizer, A Sklar. Statistical metrics spaces[J]. Pacific J.Math., 1960, 10: 313-334.

[3]B Schweizer, A Sklar. Probabilistic metrics spaces [J].North-Holland, New York, 1983.

[4]P Hajek. Metamathematics of fuzzy logic[M]. Kluwer Academic Publishers, Dordrscht, 1998.

[5]D Butnariu, E P Klement. Triangular norm-based measures and games with fuzzy coalitions [M]. Kluwer Academic Publishers, Pordrscht, 1993.

[6]J Fodor, M Roubens. Fuzzy preference modeling and multicriteria decision support[M]. Kluwer Academic Publishers, Dordrscht, 1994.

[7]L A Zadeh. Fuzzy sets [J]. Inform. and Control, 1965, 8:338-353.

[8]A Rosenfeld. Fuzzy groups[J]. J. Math. Anal. Appl., 1971, 35:512-517.

[9]J M Anthony, H Sherwood. Fuzzy groups redefined[J]. J.Math. Anal. Appl., 1979, 69: 124-130.

[10]A K Katsaras, D B Liu. Fuzzy vector spaces and fuzzy topological spaces [J]. J. Math. Anal. Appl., 1977, 58:135-146.

[11]Kourosh Nourouzi, Asadollah Aghajani. Convexity in triangular norm of fuzzy sets[J]. Chaos, Solitons and Fractals, 2008, 36: 883-889.

[12]K Atanassov. Intuitionistic fuzzy sets [J]. Fuzzy Sets and Systems, 1986, 20: 87-96.

[13]Zixin Liu, Cheng Zhang, Enmin Feng. On intuitionistic fuzzy subspaces [J]. Advances in Systems Science and Applications, 2004, 4(2): 314-318.

[14]劉自新, 張成, 馮恩民. 直覺模糊仿射空間與直覺模糊子空間[J]. 遼寧工程技術大學學報, 2005, 24(5): 778-780.

[15]沈正維, 徐國俊. 凹模糊集與凸直覺模糊集[J]. 遼寧師范大學學報, 1997, 20(4): 278-280.