測量絮團分維數的新方法

邢 軍，丁仕強，逄薪蓉，徐繼潤

（大連大學 環境與化學工程學院，遼寧 大連 116622）

0 引言

在固液懸浮體系中，固體顆粒可藉雙電層壓縮而凝聚，也可藉絮凝劑的橋鍵作用而絮凝。前者可形成較為密實的聚集物，后者則形成結構松散的絮團。Gregory[1]曾經指出，如果兩個相等的球體聚在一起，只形成啞鈴狀聚集物；如果多個顆粒發生聚集，那么聚集物形狀與結構的變化形式將迅速增加。對絮團大小與形狀的研究由來已久，而自從上世紀八十年代以來，非線性科學分形幾何及分形數學的出現，使絮團形態結構的定量表征成為可能，相關工作已有許多進展[2-4]。

由于絮團具有統計自相似的性質，因此可用分維數對其空間結構予以定量描述。常用的絮團分維數表達形式有質量分維數D（mass fractal dimension）、線度分維數D1（one-dimensional fractal dimension）、面積分維數D2（two-dimensional fractal dimension）、體積分維數D3（three- dimensional fractal dimension）[5]。

絮團的質量分維數D與有效密度ρe、特征尺寸d的關系為[6,7]：

絮團的有效密度定義為絮團密度與流體介質密度之差，絮團特征尺寸為其等效圓直徑或最大投影直徑。質量分維數可由沉降法間接測量[8-10]。

絮團在不同拓撲空間內的分維數分別與絮團投影的周長L、面積A 、絮團體積V相關聯：

D1、D2、D3通常由圖像分析法獲得[5]。圖像法是目前普遍運用的絮團分維數的測量方法。針對大量不同特征尺寸的絮團，用特征尺寸度量絮團平面投影圖像的周長，所得雙對數曲線的斜率為絮團在一維拓撲空間的分維數（線度分維數D1）；用特征尺寸度量絮團投影的面積，所得雙對數曲線的斜率為二維拓撲空間的分維數（面積分維數D2）；但絮團在三維拓撲空間的分維數（體積分維數D3）不能通過圖像法直接得到，需要先將投影面積轉換成絮團體積，例如可根據投影面積求其面積當量直徑,再換算成球體體積V。

本文將提出一種測量絮團分維數的新方法，其基本思路是通過分析固液懸浮體系的表觀粘度與絮團分形參數的關系而建立相應的數學模型，進而可通過測量體系粘度而獲得絮團分維數，這樣獲得的分維數姑且名之為粘度分維數。

1 模型的建立

1.1 粘度模型的疊加性分析

對于低濃度懸浮體系，小Einstein[11]導出體系粘度η與分散相體積分數x 的關系為：

其中η0為分散介質（連續相）的粘度。對于較濃的分散體系，固體粒子間發生相互作用，Goodwin[12]將公式（5）修正為：

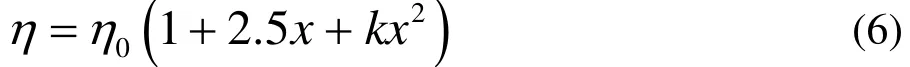
其中，系數k與顆粒聚集程度及粒間電化學作用有關。這兩個模型提供的重要啟發是：懸浮體系的總粘度可看作體系的各組成部分對粘度影響的疊加。例如，在濃度很低時，所有顆粒以完全分散的形式存在，體系的粘度為介質粘度及分散顆粒對粘度影響之和；濃度變大時，除分散顆粒外，出現了絮團，體系粘度則為介質粘度、分散顆粒對粘度的影響及絮團對粘度的影響這三部分之和。本文分析體系粘度時將沿用這一“疊加性”思路。

1.2 絮團結構的分類

為沿用對體系粘度的“疊加性”分析方法，本文將絮凝后固體物料的存在形式分為四類：（1）分散的單體顆粒或稱0-型聚集物，指絮凝后仍單獨存在的顆粒，包括從未參與絮凝的原始顆粒以及從絮團中剝落下來的單體顆粒；（2）線狀絮團或稱1-型聚集物，指由至少兩個原始顆粒形成的直線型聚集體，構成線狀絮團的所有顆粒的質量中心在同一條直線上；（3）面狀絮團或稱2-型聚集物，系由至少3個單體顆粒形成的平面狀聚集體，其所有構成顆粒的中心位于同一個平面；（4）體狀絮團或稱3-型聚集物，指至少由4個單體顆粒構成的三維聚集體，其構成顆粒的中心位于三維空間內。可以看出，這四種類型囊括了固體顆粒所有可能的存在狀態，從而可從分析各種類型聚集物（廣義的聚集物包括0-型聚集物即分散的單個顆粒）對體系粘度的貢獻著手而建立粘度與絮團分維數的數學模型。

1.3 模型建立途徑之一：碰撞理論分析

顯然，各類絮團對體系粘度的貢獻應與其數目有關，而顆粒間的碰撞理論是研究絮團數目的有力工具。此前，筆者曾分析了各類絮團的形成機制。例如，不考慮絮團碎裂的情況下，面狀絮團（2-型聚集物）的形成途徑可有圖1所示的五種可能（其中箭頭兩端的聚集物相互作用生成面狀絮團）：

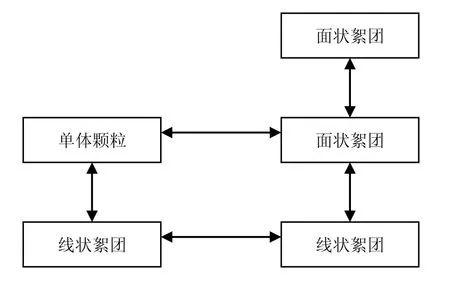
圖1 2-型聚集物的形成機制

設原始顆粒的數目濃度為n，則絮凝后體系中存在的仍然處于分散狀態的顆粒（即0-型絮團）數目正比于n，其它類型絮團的數目則與絮團中所包含的單體顆粒數有關。經過對各種絮團的詳細分析，并略去絮團數目完全表達式中的次要項，筆者得出各型絮團的數目與原始顆粒數目的關系為：

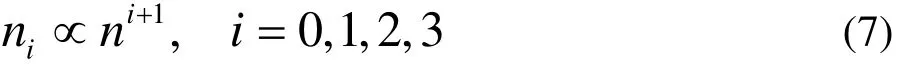
其中i為絮團類型，ni為i-型絮團的數目。在低濃度體系下，數目濃度n正比于體積分數x，而各類絮團對體系粘度的貢獻應正比于絮團數目，由疊加性原理可得體系的表觀粘度為：

其中η(i)為i-型絮團對體系粘度貢獻項的比例系數，具有粘度的量綱；ηm為純分散介質的粘度。巧合的是，該模型中的i既是絮團類型，又與絮團的拓撲維數暗合。雖然在模型的導出過程中并未提及絮團維數的問題，但這種“巧合”使我們有興趣繼續探索體系粘度與絮團維數的關系。

1.4 模型建立途徑之二：繞流阻力分析

該分析方式旨在直接建立形如式(8)的體系粘度與絮團拓撲維數的關系，進而建立粘度與絮團分維數的數學模型。

我們從單個顆粒自由沉降時的 Stokes阻力公式入手。顆粒對流體的繞流阻力（即 Stokes分析時的流體對顆粒沉降的阻力）為：

其中d 為顆粒直徑，代表顆粒的特征尺寸L0；v為顆粒的自由沉降速度（或流體繞流速度）。記無顆粒存在時即純流體的粘度為ηm，顆粒的存在使顆粒附近的流體流動受阻，即流體粘度較純流體有相應的增加：

從(9)、(10)兩式可知顆粒的存在對流體粘度的貢獻為：

記單體顆粒、線狀絮團、面狀絮團及體狀絮團的數目分別為n0，n1，n2，n3，各型絮團的平均特征尺寸分別為L0,L1，L2，L3，繞流阻力分別為R0，R1，R2，R3，其中L0,R0已如前述。雖然還很難像處理球形顆粒那樣經過嚴格的理論推導得出各型絮團的繞流阻力，但可以預見，線狀絮團、面狀絮團、體狀絮團的繞流阻力應分別與其長度、面積、體積成正比，即

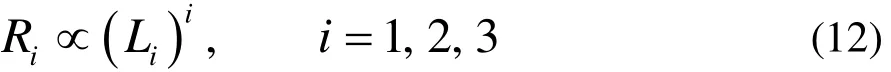
這里的i=1,2,3分別為對應的各型絮團的拓撲維數。

不難理解，各型絮團的數目及絮團的平均特征尺寸（除單體顆粒外）均與原始顆粒數n成正比：

各類絮團的總繞流阻力為：

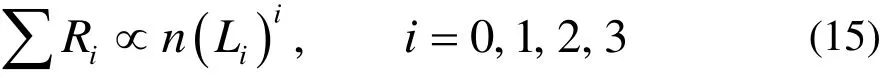
類比與公式(11)，各類絮團對體系粘度的貢獻為：

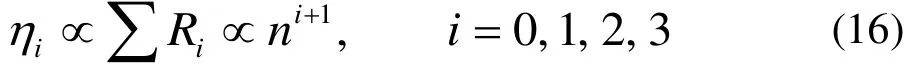
考慮到低濃度體系的n∝x，該式可寫成等式：

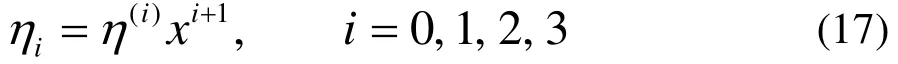
于是體系的總粘度如下：

這與循顆粒碰撞途徑導出的公式(8)在形式上完全相同，但式中濃度的指數i已在導出過程中明確為相應絮團的拓撲維數。

2 模型的討論

2.1 分維數的引入

考慮到線狀絮團、面狀絮團及體狀絮團的分形特征，其對應的拓撲維數可用各自的分維數Dfi(i=1,2,3)替代，則(18)式成為：

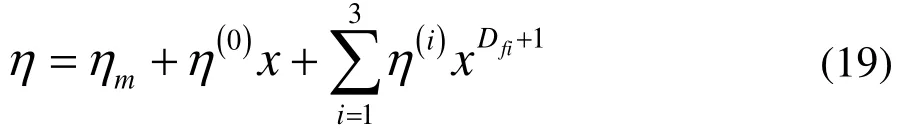
2.2 高濃度體系下的修正

對高濃度體系，只要以固體物料的體積比粘度（即固體物料體積與液體體積之比）X代替體積分數x，則n∝X，以上的分析過程不變，于是式(19)成為：

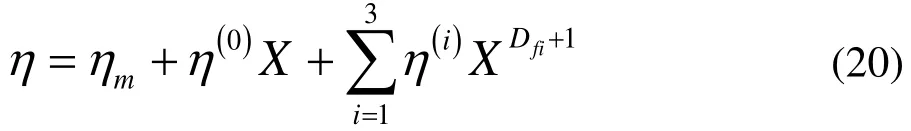
2.3 多分散體系下的修正

對于多分散體系（即原始顆粒粒度不同的體系），只要以顆粒的平均粒度代替上述推導過程中的單體顆粒特征尺寸，仍可得到式(19)或(20)的結果，當然，式中的比例系數及各類絮團的分維數在具體數值上會有所不同。

2.4 模型與小Einstein模型的統一性

在模型(19)或(20)中，若顆粒濃度很低，則濃度的高次項可以忽略不計（即基本不存在顆粒的聚集現象），則模型回歸到小Einstein粘度模型(5)。

3 模型的意義

3.1 提供了測量絮團分維數的新方法

該模型首次將表觀粘度這一易于測量的宏觀參數與各類絮團的分維數聯系起來，提供了一種測量絮團分維數的新方法，不妨將這樣測出的分維數命名為粘度分維數，以區別與傳統的質量分維數、孔隙表面分維數等。

3.2 對不同類型絮團分維數的同步測量

模型首次將絮團分為線狀絮團、面狀絮團及體狀絮團等三類，在一個數學模型里同時包括了這三類絮團的分維數并可定量測量之。

3.3 對測量過程的簡化

該模型測得的絮團分維數反映了所有同類絮團的影響，不需像其它方法那樣需對大量絮團個體測量后再統計處理；此外，由于應用該模型測量時，僅需測量體系粘度一個參數，避免了其它方法測量分維數時需同時測量兩個參數而導致的誤差。

3.4 使對絮團組成的定量分析成為可能

由于將各類絮團以及單體顆粒對體系粘度的影響分別表示，從而依據模型中各類絮團對體系粘度的相對貢獻可評估不同絮團的相對組成。

關于該模型的實驗研究將另文報道。

4 結語

絮團分維數是描述絮團分形結構的定量參數。本文通過不同途徑導出的絮凝處理后懸浮液表觀粘度與絮團分維數的數學模型，提供了測量絮團分維數的一種新方法。這種新方法可同時測出不同類型絮團的分維數，這是其它方法所不能做到的。這種方法還為研究絮凝后不同類型絮團的定量組成提供了潛在的分析工具。

[1]John Gregory. The role of floc density in solid-liquid separation [J]. Filtration and Separation, 1998, 35(4):367-371.

[2]Meakin P. Fractal aggregates [J]. Adv. Colloid Interface Sci.,1988, 28: 249-331.

[3]Sterling M C, J S Bonner, A N S Ernest, et al. Application of fractal flocculation and vertical transport model to aquatic sol-sediment systems [J]. Water Research, 2005, 39: 1818-1830.

[4]John Gregory. Optical monitoring of particle aggregates [J].Journal of Environmental Sciences, 2009, 21(1): 2-7.

[5]WANG Yili, LU Jia, DU Baiyu, et al. Fractal analysis of polyferric chloride-humic acid (PFC-HA) flocs in different topological spaces [J]. Journal of Environmental Sciences,2009, 21(1): 41-48.

[6]Meakin P. Fractals, Scaling and Growth Far From Equilibrium[M]. Cambridge: Cambridge Univ. Press, 1998.

[7]John Gregory. Optical monitoring of particle aggregates [J].Journal of Environmental Sciences, 2009, 21(1): 2-7.

[8]Li X Y, Logan B E. Permeability of fractal aggregates [J].Environmental Science and Technology, 2001, 35(14): 3373-3380.

[9]Sterling M C, J S Bonner, A N S Ernest, et al. Aplication of fractal flocculation and vertical transport model to aquatic sol-sediment systems [J]. Water Research, 2005, 39: 1818-1830.

[10]Federico Maggi. Variable fractal dimension: A major control for floc structure and flocculation kinematics of suspended cohesive sediment [J]. Journal of Geophysical Research,2007, 112, C07012, doi:10.1029/2006JC003951.

[11]A Einstein. Investigation on Theory of Brownian Movement[M]. New York: Ed. R. Furth Dover, 1956: 55.

[12]J W Goowin. The Rheology of Dispersion [J]. J. Colloid Sci.,1975, 2: 246-293.

[13]Shiqiang Ding, Qingna Li, Xinrong Pang, et al. A Research on the Morphology and Composition of Flocs ( Part 1: Floc Breakage Disregarded) [J]. Advanced Materials Research,2013, 726-731: 1566-1572.

[14]Shiqiang Ding, Yuanyuan Wei, Xinrong Pang et al. A Research on the Morphology and Composition of Flocs( Part 2: Floc Breakage Included) [J]. Advanced Materials Research, 2013, 726-731: 1585-1590.