碳纖維板-混凝土界面黏結性能的試驗研究與有限元分析*

尚守平，李知兵,2?，彭 暉

(1．湖南大學 土木工程學院，湖南 長沙 410082；2. 湖南工學院 建筑工程與藝術學院，湖南 衡陽 421002； 3. 長沙理工大學 土木與建筑學院，湖南 長沙 410004)

近年來外貼碳纖維板加固在建筑及橋梁結構加固補強中應用廣泛，在碳纖維板與混凝土間傳遞應力的界面黏結，對加固結構受力性能起著至關重要的作用.為精確預測加固結構的力學行為，需要深入把握黏結界面的受力行為.因此研究人員對加固結構的受力性能和力學行為開展了大量研究[1-6]，設計了各種界面黏結性能的試驗測試裝置并通過試驗考察了界面受剪行為；推導了碳纖維板加固鋼筋混凝土受彎構件界面應力的計算公式；也針對黏結界面的特點建立了平面有限元模型分析界面剪應力-滑移關系.已有的單剪試驗方法操作較繁瑣，試驗結果受試驗設備和試件形狀影響較大；已完成的有限元分析通常忽略黏結層的受剪滑移，直接在界面將兩種材料節點耦合，或將整個結構簡化成平面進行分析[7-9]；現有的剪應力-滑移計算理論模型較多，考慮的參數較片面且不一致.鑒于此，本文參考Yun等人[10]的試驗設計，實施了雙面粘貼碳纖維板的混凝土棱柱體組合試件的受剪試驗；研究了界面受剪條件下黏結應力變化規律；得到了黏結-滑移曲線，定義了適用黏結界面受力狀態的彈簧單元組，建立了相應的三維有限元模型，并將分析結果和試驗結果進行了對比分析；基于已有的黏結-滑移本構關系進行了本文試驗所得到的黏結-滑移曲線值擬合，比較了不同本構模型與試驗結果的吻合程度.

1 碳纖維板-混凝土界面雙剪試驗

1.1 試件設計

本文采用的試驗形式為界面雙剪試驗.試件由2個尺寸為150 mm×150 mm×300 mm的混凝土棱柱體對接組成；在棱柱體的2個相對側面分別粘貼了由西卡公司生產的，截面尺寸為50 mm×1.2 mm的Sika-S512型碳纖維板；棱柱體端部中心埋設有便于試驗機夾持的螺紋鋼拉桿；為防止試件在加工和試驗過程中碳纖維板出現偏心受力，并保證試驗過程中2個混凝土棱柱體只出現相對豎向位移，特進行了以下處理：在2個混凝土棱柱體端部光面上各用結構膠黏有一塊同棱柱體截面大小的10 mm厚方形鋼板，鋼板4個對應角點分別垂直焊有同尺寸鋼桿，再通過直徑略大于鋼桿的銅質套筒連接對應鋼桿實現2個棱柱體的準確對中.試件如圖1所示.

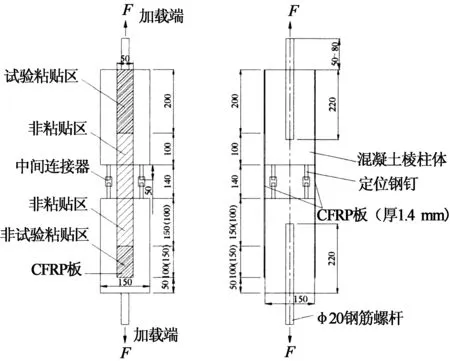
圖1 試件設計

4個試件所使用的混凝土標號為C30，實測28 d立方體試塊抗壓強度為31.5 MPa, 30.5 MPa, 32.4 MPa, 32.5 MPa.主要材料力學性能見表1.為控制界面剝離現象出現的位置，B區粘貼長度B1B2為200 mm，大于Chen和Teng公式[3]計算的有效黏結長度Le=190.1 mm，而A區粘貼長度小于B端，則理論上A區首先出現開裂情況；為避免界面出現剝離時引發棱柱體邊緣混凝土撕裂，對整個剝離行為產生影響，特在粘貼區之前設置一段非粘貼區A1B1.同時設計制作了A區不同粘貼區長度和相同膠層厚度的4組試件進行對比試驗，試件具體參數見表2.

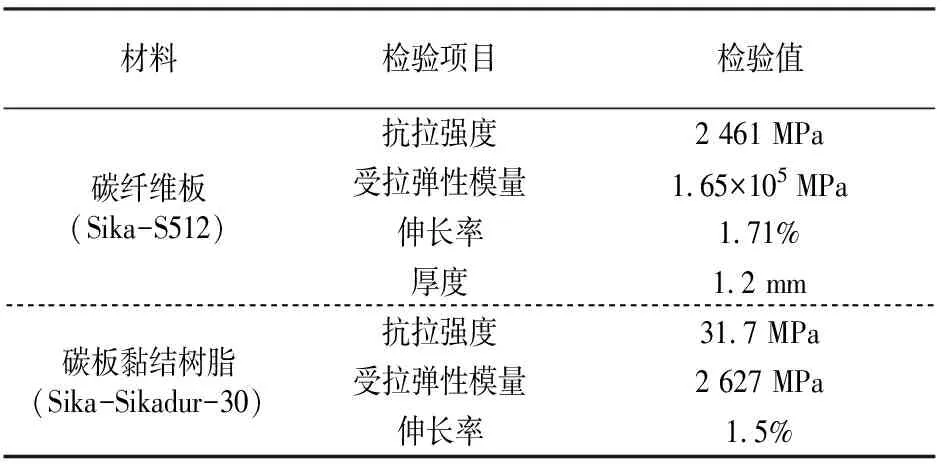
表1 試件材料力學性能

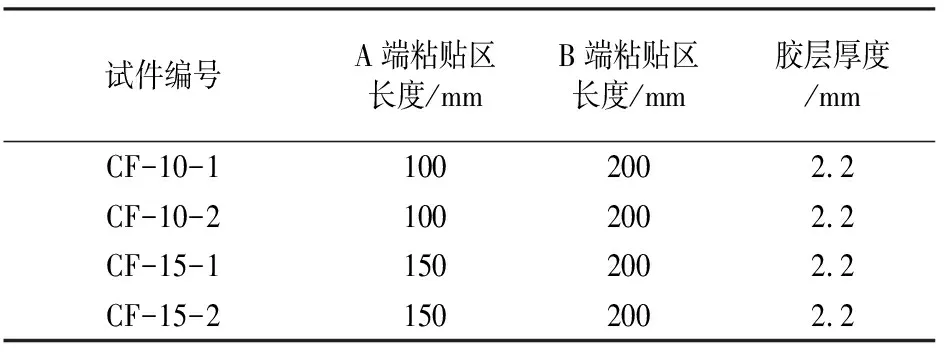
表2 試件粘貼區長度設置

1.2 測點布置及試驗加載過程

界面的黏結應力一般由碳板粘貼區部分的應變間接反映[11-13].因設置粘貼長度相對較小的A區為實驗區，故在試驗過程中主要觀測A區的碳纖維板應力變化和界面的剝離破壞現象.主要通過在A區碳纖維板上連續布置的5 mm×3 mm規格的電阻應變片采集，試件CF-15-1/15-2粘貼區碳纖維板應變片具體布置如圖2所示.界面的滑移量一般也可以通過碳板應變反映，但是為了準確測得滑移量，本實驗中采用在靠近A2端2個應變片之間布置由鋼鐵研究總院生產的電子引伸計來測量碳板與混凝土之間的滑移量.

為了得到碳纖維板與混凝土界面之間的裂縫出現時間、發展規律以及破壞形式、破壞特征等，試驗嚴格采用分級加載制度.首先預加載2 kN，預載2～3次，檢查試件2片碳纖維板應變是否正常.從2 kN開始按3 kN每級的分級加載至理論極限荷載的一半，再以2 kN每級加載捕捉界面開裂荷載和極限荷載.在每級加載完畢之后，需等待5～8 min，待應變值穩定下來再記錄應變值.試驗加載過程采用美國MTS公司810多功能材性試驗機，每級荷載值可通過配套計算機軟件精確控制(如圖3所示).

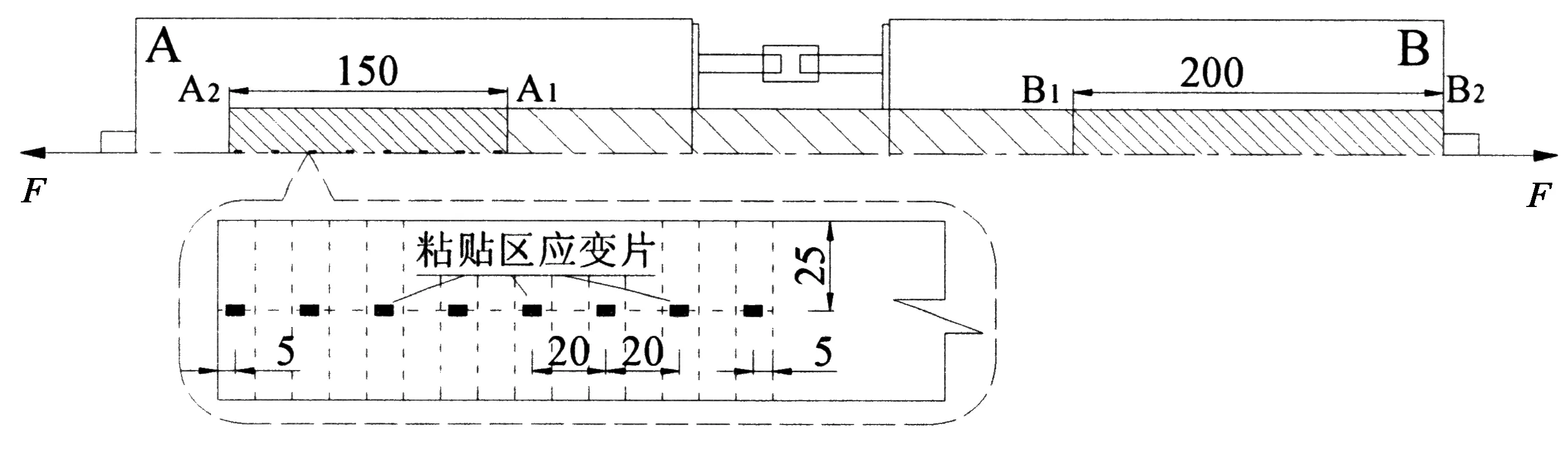
圖2 試件CF-15-1/15-2粘貼區碳纖維板應變片測點布置(單位：mm)

圖3 試驗加載裝置

1.3 試驗結果及分析

在試驗中可以觀察到界面裂縫首先在A區A1點附近出現，試件CF-10-1和CF-10-2(粘貼長度為100 mm)分別在加載至26 kN和28 kN時觀察到黏結界面裂縫，而CF-15-1和CF-15-2(粘貼長度為150 mm)的界面開裂荷載分別為32 kN和36 kN.隨著荷載的繼續增加，界面裂縫迅速向板端發展.最終破壞狀態為“啪”的聲響伴隨黏結膠層和混凝土界面的完全剝離，如圖4所示，剝離的碳纖維板在A1點附近會附帶少量混凝土下來，因破壞過程突然，板端甚至會有部分碳纖維從碳板上被撕扯下來.實測粘貼區長為100 mm的試件極限剝離承載力為33.2 kN和37.1 kN，粘貼區長為150 mm的試件的極限剝離承載力為44.5 kN和46.4 kN.這里開裂荷載約為極限抗力的24%，亦即，當拉伸應力超過碳纖維板強度的24%時，碳板已開始從混凝土表面剝離，如果沒有錨具，預應力將不能有效地傳遞到混凝土構件上.

(a) 端部界面剝離

(b)界面破壞后碳纖維被撕扯下來

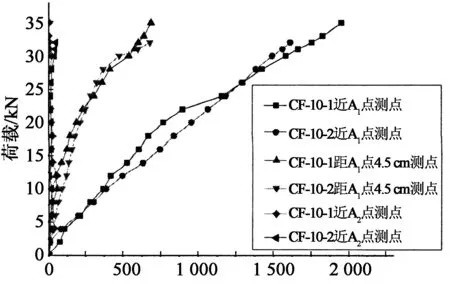
圖5描繪了試件CF-10-1/10-2粘貼區碳纖維板測點的荷載-應變曲線.由圖可見，當荷載值較小時，CFRP板、黏結膠層和混凝土共同承受荷載作用，此時各位置應變同步增加.隨著荷載的加大，混凝土表面拉應力、CFRP板與混凝土之間的黏結應力也不斷增大，此時不同位置的應變發展呈現不同的規律：A粘貼區近A2點碳纖維板自由端應變較小，隨荷載增加沒有明顯變化；近A1點碳纖維板應變和粘貼區中部應變則隨荷載增大呈線性變化.當荷載達到一定值時，界面之間應力分布開始變得不均勻而在薄弱部位發生開裂或損傷，此時界面應力重分布.從圖上也可觀察到近A1點碳纖維板應變和粘貼區中部應變在加載過程中先后出現拐點，反映了界面裂縫從加載點向粘貼區中間擴展的現象，且拐點對應荷載值與試驗觀測到的開裂荷載很接近，同樣的規律也在試件CF-15-1/15-2上得到反映.

試件在25%和50%極限荷載作用下，沿板長方向各測點的碳纖維板應變分布如圖6和圖7所示，試驗中每個試件均采集了2面的碳纖維板應變值，經比較發現對應點的應變較一致，故將對應點應變值取均值以便與其他試件比較.

CFRP應變/με

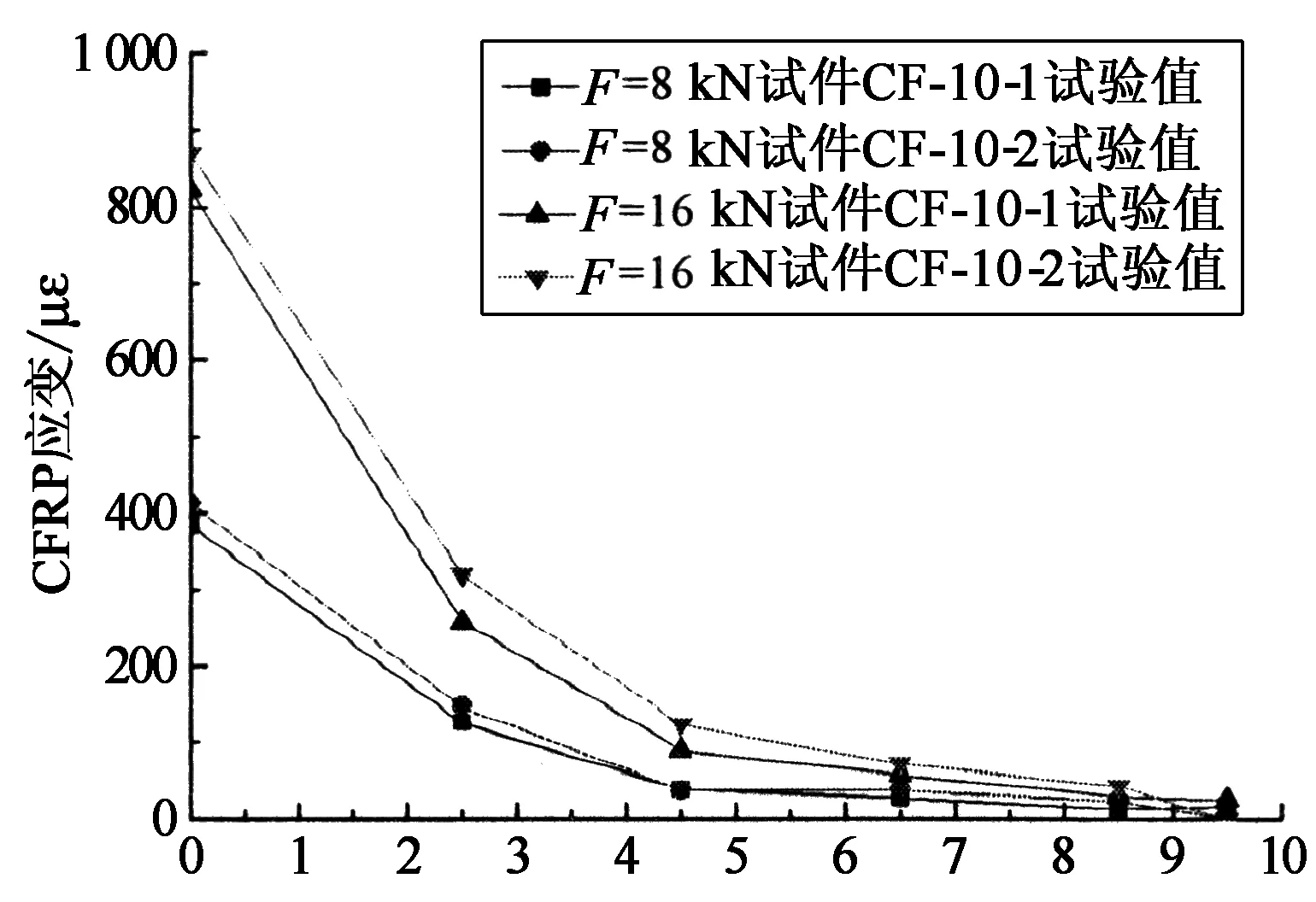
測點與A1點距離/cm

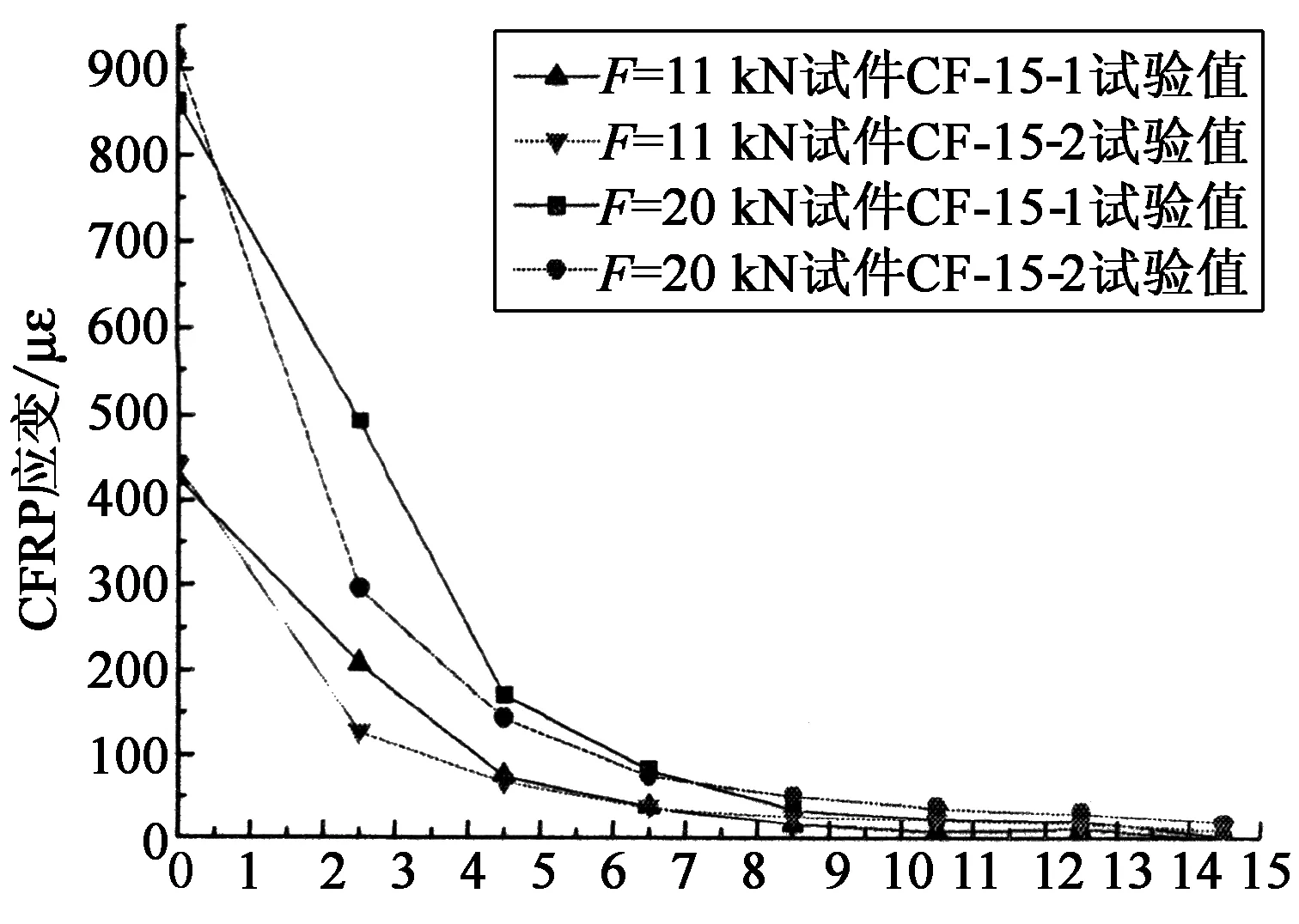
測點與A1點距離/cm

由上圖試驗結果可看到：在界面開裂之前，不同粘貼區長度的試件在A粘貼區0～10 cm范圍內碳板應變分布趨勢較接近，沿板長方向大致呈指數衰減分布；而試件CF-15-1/15-2在A粘貼區10～15 cm的范圍內碳板應變基本不隨荷載變化，提供了一定的強度儲備，故其開裂荷載和極限荷載更高.總體而言，在缺乏適當錨固的條件下，黏結樹脂對于外貼碳纖維板能提供的黏結承載力較為有限，為充分發揮碳纖維板的高強性能，可考慮采用錨具對碳纖維板進行錨固.

2 有限元模型分析

2.1 CFRP-混凝土界面單元選取

CFRP與混凝土之間的受力機理復雜，已有的部分有限元模型為簡化分析，未考慮界面的黏結滑移.這就使得準確模擬和分析界面黏結性能變得不可能.隨著界面單元的引入，利用有限元分析CFRP與混凝土之間的受力機理變得可行[14-15].有限元分析中，CFRP-混凝土模型的建立目前較為合理的是使CFRP與混凝土共節點方式，為了反映CFRP-混凝土之間的黏結滑移關系，非線性2維界面單元被置入共用節點之中.非線性2維界面單元很多，應用較為廣泛的包括彈簧單元、離散束單元、連續單元等.Ahmed Godat等[16]對這3種單元進行了數值模擬，發現3種界面單元都能夠有效地模擬界面黏結滑移，但是存在一定的差異.

本文在已有的有限元模型基礎上，考慮使用彈簧單元組連接混凝土和碳纖維板以模擬界面的受力.該彈簧單元組如圖8所示，通過在混凝土棱柱體和碳纖維板模型對應節點之間設立法向和切向2個正交單向彈簧組成.

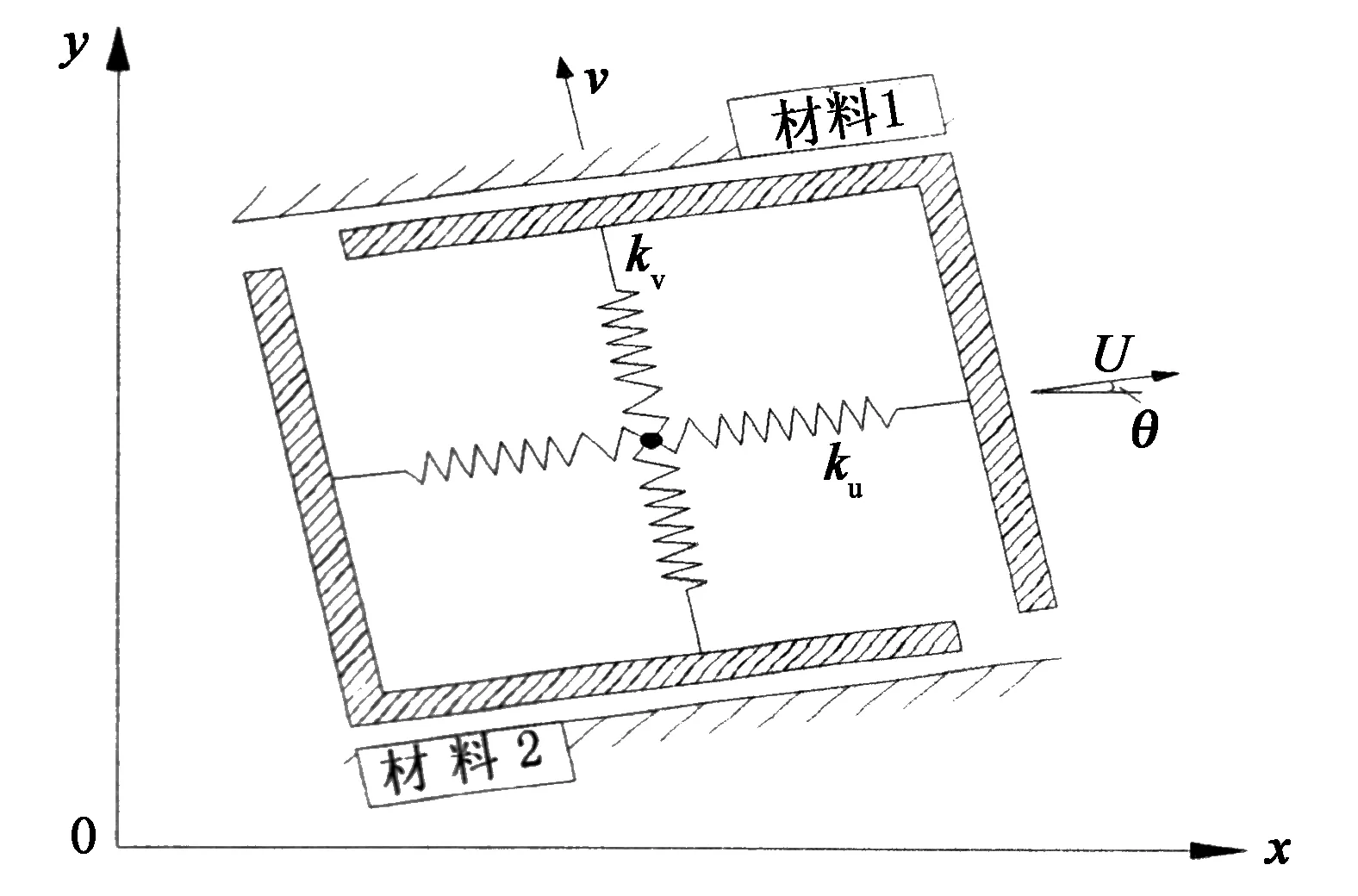
圖8 正交彈簧組示意圖

彈簧單元采用可以設置F(荷載)-D(變形)曲線來定義材料本構關系的COMBIN39單元，彈簧的自由度方向通過在實常數中設置單元的關鍵字選項KEYOPT(n)=x(n,x的設置參考ANSYS單元手冊)來控制，如圖9所示.

對于切線彈簧，每根彈簧單元的剛度表現為黏結-滑移關系的一階導數，k=dF/dδ，又F=τ(δ)×A，τ(δ)為界面的黏結滑移關系模型，A為每個彈簧的作用面積．如圖10所示每個彈簧的位置不同導致彈簧單元等效作用面積A不同，故所選取的界面有3種不同剛度，根據彈簧不同位置可以定義為角點彈簧kj, 邊線彈簧kb, 中間彈簧kz，對于膠層作用面積分別為：Aj，Ab，Az，其中Aj=a×b/4，Ab=a×b/2，Az=a×b，式中，a,b分別表示膠層(同CFRP板)單元網格縱向尺寸和橫向尺寸.界面彈簧單元的布置和作用面積如圖10所示.

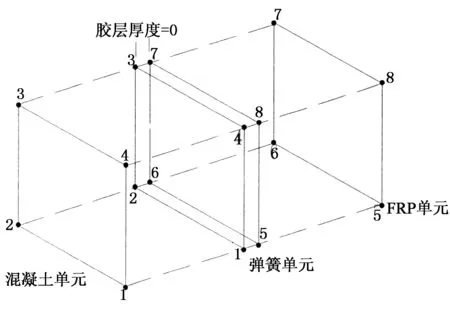
圖9 CFRP-混凝土單元連接示意圖

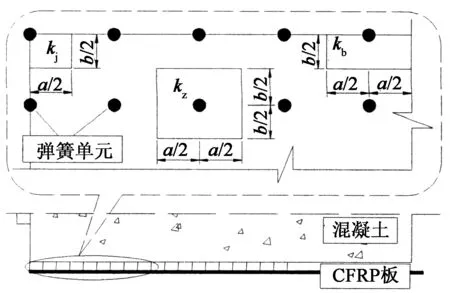
圖10 界面彈簧單元布置

2.2 靜載下的界面局部黏結-滑移關系

界面黏結滑移本構關系決定了FRP片材與混凝土之間的黏結行為，也是通過數值模擬分析界面黏結性能的基礎．國內外眾多研究人員也通過試驗與理論研究構建了不同的黏結滑移本構模型，比較典型的有Popovics模型、雙線性模型、三線性模型、陸新征精細有限元模型、T. Ueda[14]所建議模型等.然而由于不同模型存在尺寸效應，直接采用經典黏結滑移模型不能較好地與本試驗結果吻合.盡管直接從雙剪或單剪實驗獲得界面的黏結滑移曲線比較困難，但是大量的學者結合理論及實驗得到了局部的黏結滑移本構關系，基于試驗結果，不少學者以經典的黏結滑移本構關系為基礎，對黏結滑移本構模型進行了修正，比如Nakaba[17]，Monti[18]以及Savioa[19]等以Popovics模型為基礎得到了其試驗的黏結滑移本構關系.本文以試驗得到的局部黏結滑移本構關系為基礎，通過分析擬合得到基于幾種經典黏結滑移本構關系的數學模型.

局部黏結滑移關系對于確定界面的黏結性能的本構關系是尤為重要的一步.現有的獲得界面黏結滑移曲線的一種方法是通過分析FRP的應變分布曲線得到τ-s關系. Dai等[20]在FRP-混凝土雙剪試驗中通過整合試驗中的應變片數據結合以下公式(1)和(2)可以得到其黏結滑移本構模型.本文也采用 Dai等[20]在文章中提到的公式計算靜力下局部黏結應力，并結合引伸計測得的相應滑移量，得到了本文試驗的黏結滑移關系.

CFRP板上應變片間距是10 mm，局部的滑移量通過引伸計測出，并通過CFRP板應變分析驗證.第i個應變片位置的滑移值為：

(1)

第i個應變片位置局部黏結應力為：

(2)

式中:si為第i個應變片位置處的CFRP板與混凝土之間的局部滑移量；Δx為應變片間距；ε0為黏結區自由端的應變片值；εj(j=1,i)為沿CFRP板長方向第j個應變片值；τi為第i個應變片位置處的CFRP板與混凝土之間的黏結應力；Ef和tf分別為CFRP板的彈性模量和厚度.通過分析試驗結果，得到了碳纖維板-混凝土的局部黏結滑移曲線，并轉換成有限元當中所采用的各切向彈簧的荷載-變形曲線如圖11和圖12所示.

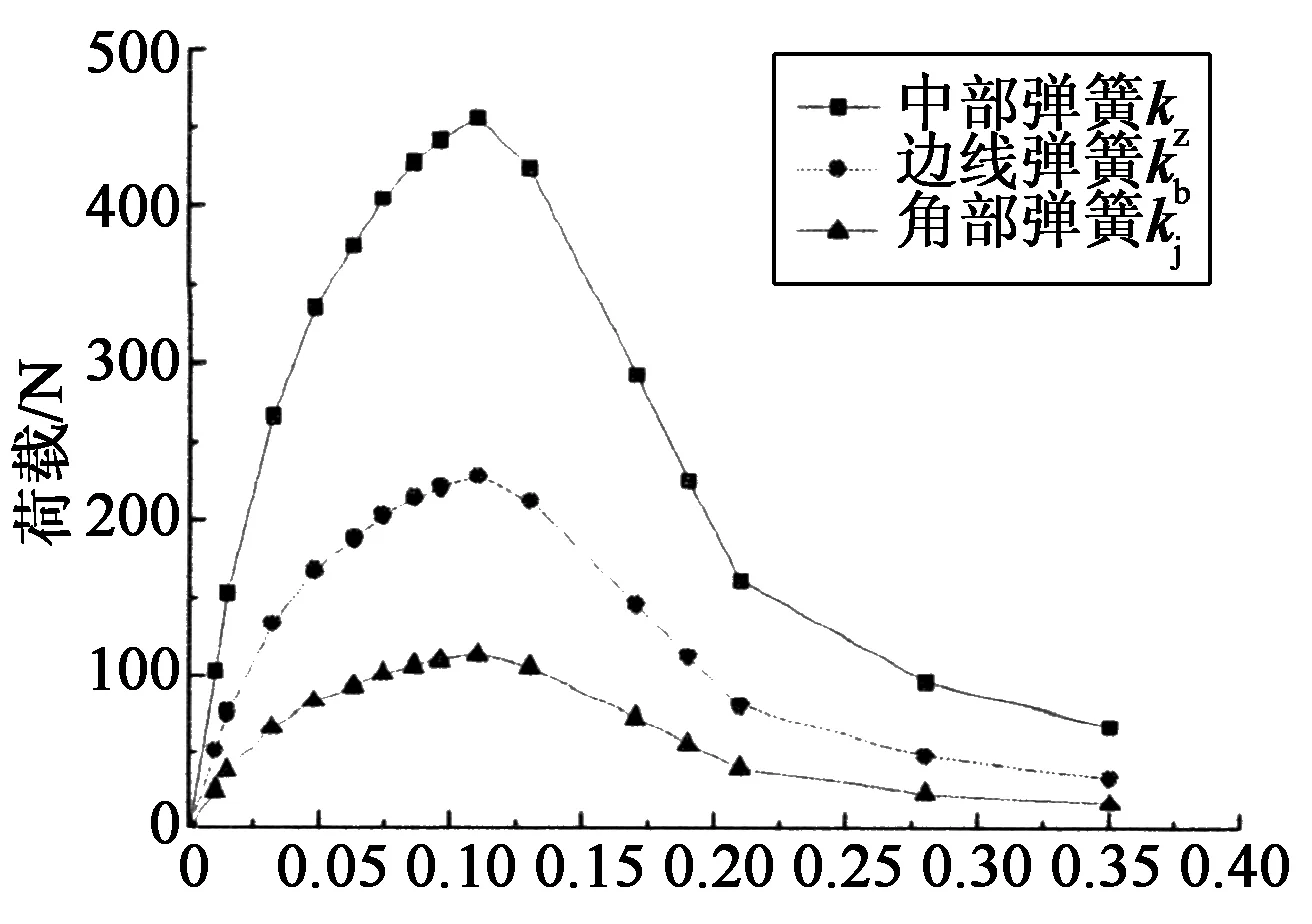
滑移量/mm

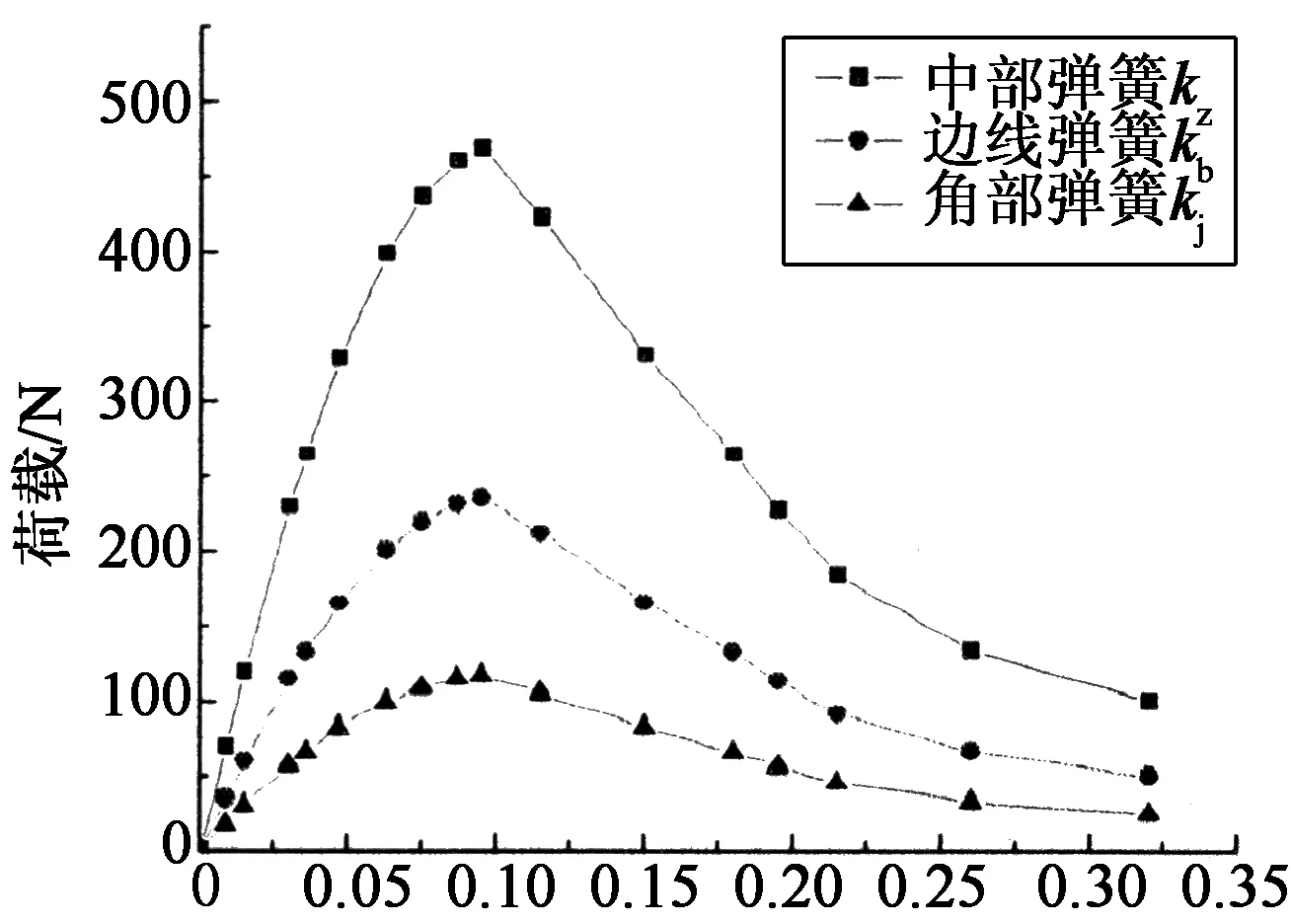
滑移量/mm

在界面受剪分析中發現法向彈簧的剛度對碳板應變的分布大小幾乎沒有影響，彈簧單元更多地是模擬沿板長方向的滑移，故在計算中取其剛度值略大于切向彈簧的剛度即可.

2.3 試件有限元模型

基于上述工作，本文使用通用有限元軟件ANSYS建立了試件的有限元模型(如圖13所示).模型中根據試驗類型和試件結構特點分別模擬了混凝土、鋼拉桿、碳纖維板和環氧樹脂膠層4種材料.考慮到界面剝離大多出現在膠層-混凝土界面，且會扯下薄層混凝土，所以混凝土單元采用可以模擬混凝土開裂的SOLID65單元；試件的Φ20螺桿采用雙線性實體單元SOLID45模擬；碳纖維板采用具有大變形功能的SHELL63單元模擬.

圖13 有限元模型

3 分析結果和試驗值對比

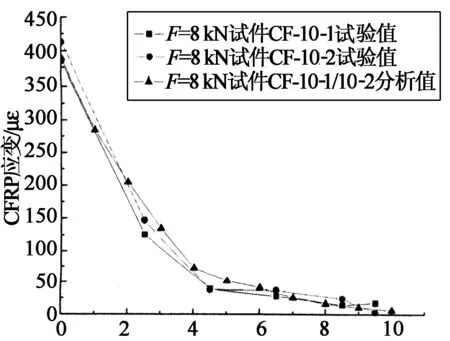
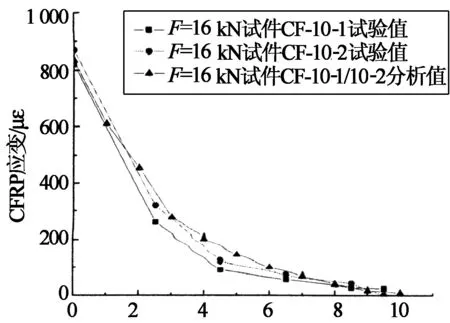
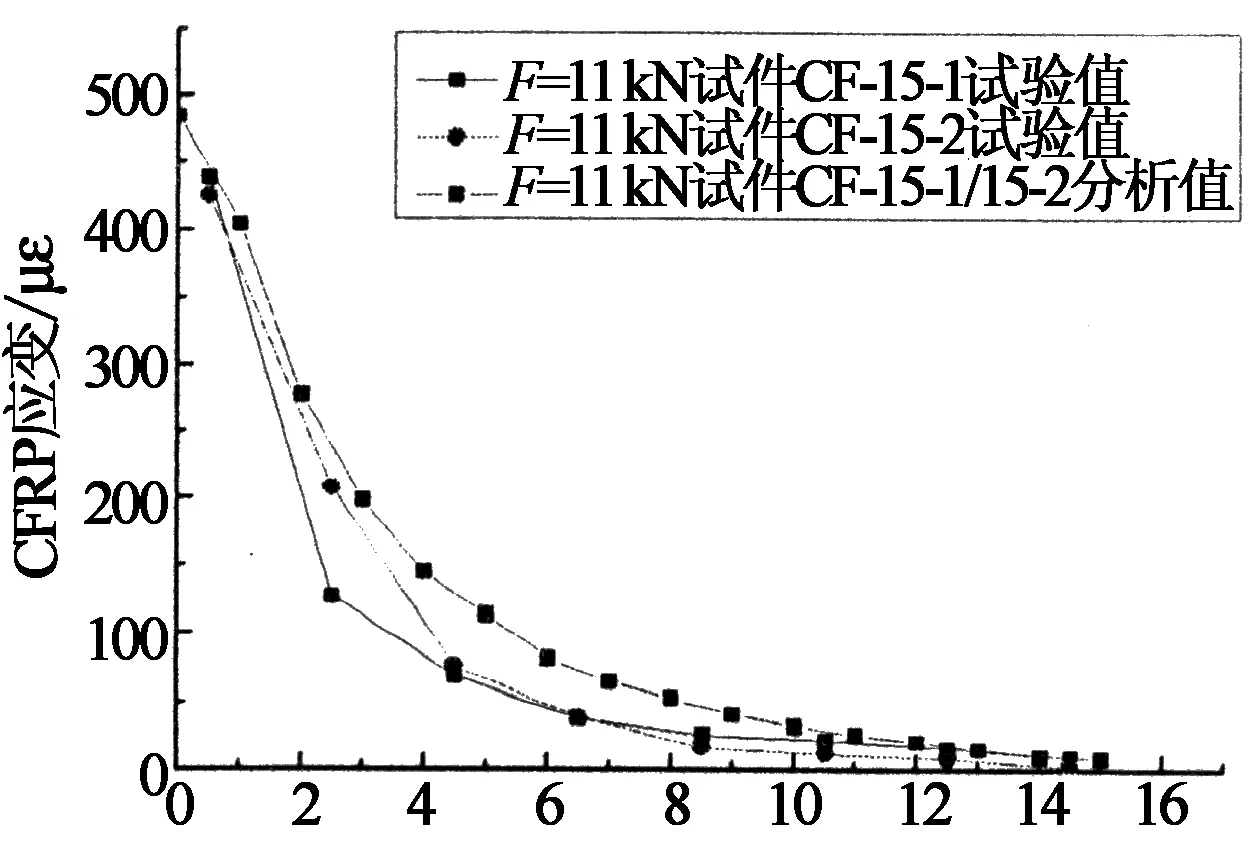
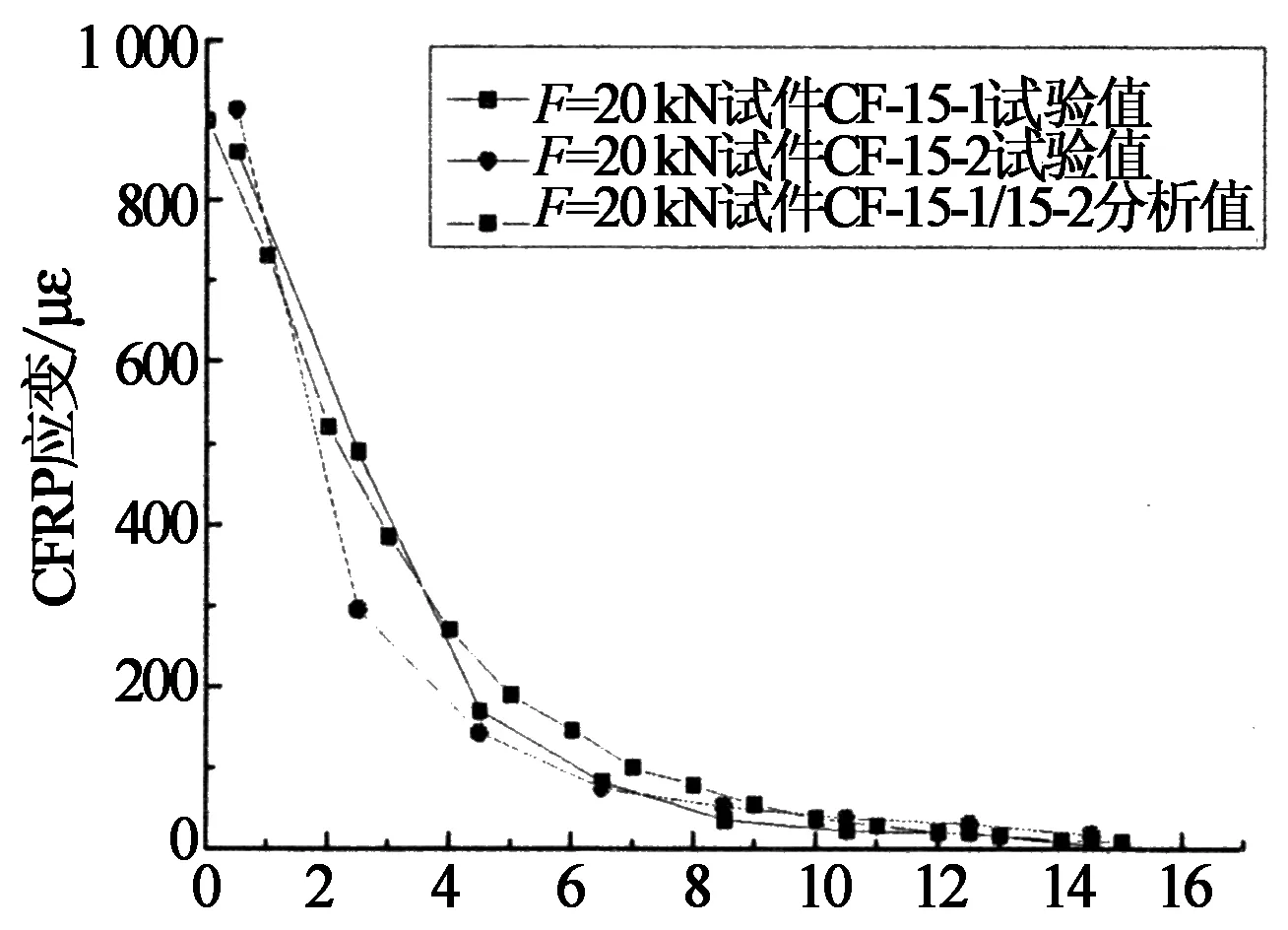
在試驗研究和有限元分析基礎上，本文對25%和50%極限荷載下沿板長方向碳纖維板的應變分布的試驗結果和分析結果分別進行了對比，如圖14和圖15所示.

測點與A的距離/cm

測點與A1的距離/cm

測點與A的距離/cm

測點與A1的距離/cm

由圖14和圖15可以看出，本文試驗結果和有限元模型計算結果吻合較好，碳纖維板應變分布規律和應變值比較接近.試驗值和計算值都反映了A粘貼區黏結層近A1點切向應力較大，從計算模型中也可以觀察到界面裂縫首先在此端混凝土出現，而近A2點黏結層切向應力幾乎為0.提取有限元分析結果：CF-10-1/10-2試件和CF-15-1/15-2試件的極限承載力分別為36.5 kN和46 kN，這與CF-10-1/10-2試件和CF-15-1/15-2試件的平均試驗承載力35.2 kN和45.5 kN比較接近，進一步說明了試驗得到的局部界面黏結滑移曲線關系符合本實驗的黏結滑移本構關系.

4 黏結滑移本構模型比較

在前述工作基礎上，本文根據試驗得到的界面黏結滑移關系，擬合確定了Popovics模型、雙曲線模型、T. Ueda模型等界面黏結滑移模型的相關系數，并將擬合結果與試驗結果進行了比較.

4.1 Popovics模型

Popovics表達式如式(3)所示，Nakaba[17], Monti[18]以及Savioa[19]都應用該模型對碳纖維加固混凝土結構界面黏結滑移曲線進行過擬合，也均得到了與試驗比較相近的結果.

τ=τmaxas/s0/[(a-1)+(s/s0)a].

(3)

式中：τ為黏結應力；τmax為最大黏結應力；s為局部滑移量；s0為最大黏結應力對應的滑移量；a為回歸系數，通過本文試驗結果擬合CF-10-1/10-2的a值為3.4，CF-15-1/15-2 的a值為3.42.

4.2 雙曲線模型

典型的雙曲線模型由上升段和下降段組成，故可分別用不同的函數表示.雙曲線基本表達式為：

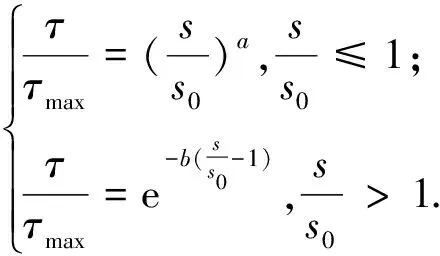
(4)

式中：a，b均為回歸系數，本次試驗擬合值為：CF-10-1/10-2試件的a=0.57,b=0.66 ,CF-15-1/15-2試件的a=0.621，b=0.676.

4.3 T.Ueda模型

T. Ueda[14]所建議的黏結滑移本構關如下：

τ=2BGf(e-Bs-e-2Bs).

(5)

其中，

B=0.846(Eftf)0.108(Ga/ta)0.833；

τmax=0.5BGf，s0=0.693/B；

Ga/ta=Gp·Gad/(Gptad+Gadtp)；

式中:A表示膠層單元作用面積；τ表示膠層的剪應力;s表示界面的滑移量;f(s)是s的函數；B表示材料性能常數;Gf表示界面破壞能；Gp和Gad分別表示碳板和膠層剪切模量；Ep和Ead分別表示碳板和膠層彈性模量；tp和tad分別表示碳板和膠層材料的厚度；Ga/ta為界面的剛度系數.

由于式(5)中考慮的影響界面黏結滑移的參數較多，而本課題組未進行大量的試驗對影響界面黏結性能的參數進行分析，但是大量學者在進行界面黏結滑移分析時發現，膠層剛度對界面黏結滑移關系影響較大，而大多數黏結滑移本構關系未曾考慮膠層剛度對界面黏結性能的影響，尤其是在疲勞循環過程中膠層剛度對界面黏結性能影響最為顯著，故在黏結滑移本構關系中引入膠層剛度參數更能夠體現界面黏結性能的本質.這里簡單地以公式(6)為基礎，設定3個回歸分析變量，具體表達式如下：

τ=c(e-as-e-bs).

(6)

式中：a,b,c為回歸系數.回歸分析得：CF-10-1/10-2試件的a=11.31，b=11.64，c=387.6，CF-15-1/15-2試件的a=11.67，b=11.98，c=432.9.

4.4 Dai and Ueda模型[20-21]

Dai和Ueda結合雙曲線模型，從影響界面黏結性能的多重因素出發，提出了具體的黏結滑移本構關系，表達式如下：

(7)

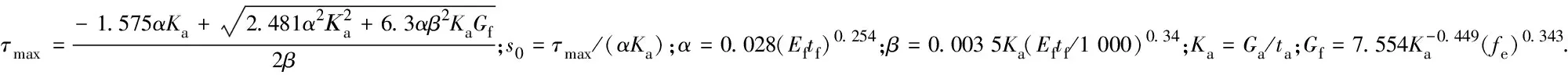
Dai和Ueda模型的上升段與雙曲線模型完全相同，對于其下降段取β為回歸系數，回歸得到CF-10-1/10-2試件的β為6.757，CF-15-1/15-2試件的β為7.123 5.

比較Dai和Ueda模型和雙曲線模型發現，Dai 和Ueda模型考慮了所有影響界面黏結性能的因素，Dai和Ueda在研究中發現界面膠層剪切剛度對界面黏結性能至關重要，相反FRP剛度對界面黏結性能影響不大，故在黏結滑移本構模型中考慮了界面膠層剪切剛度的影響.

將以上幾種回歸分析曲線與試驗得到的黏結滑移曲線展現在圖16及圖17中.

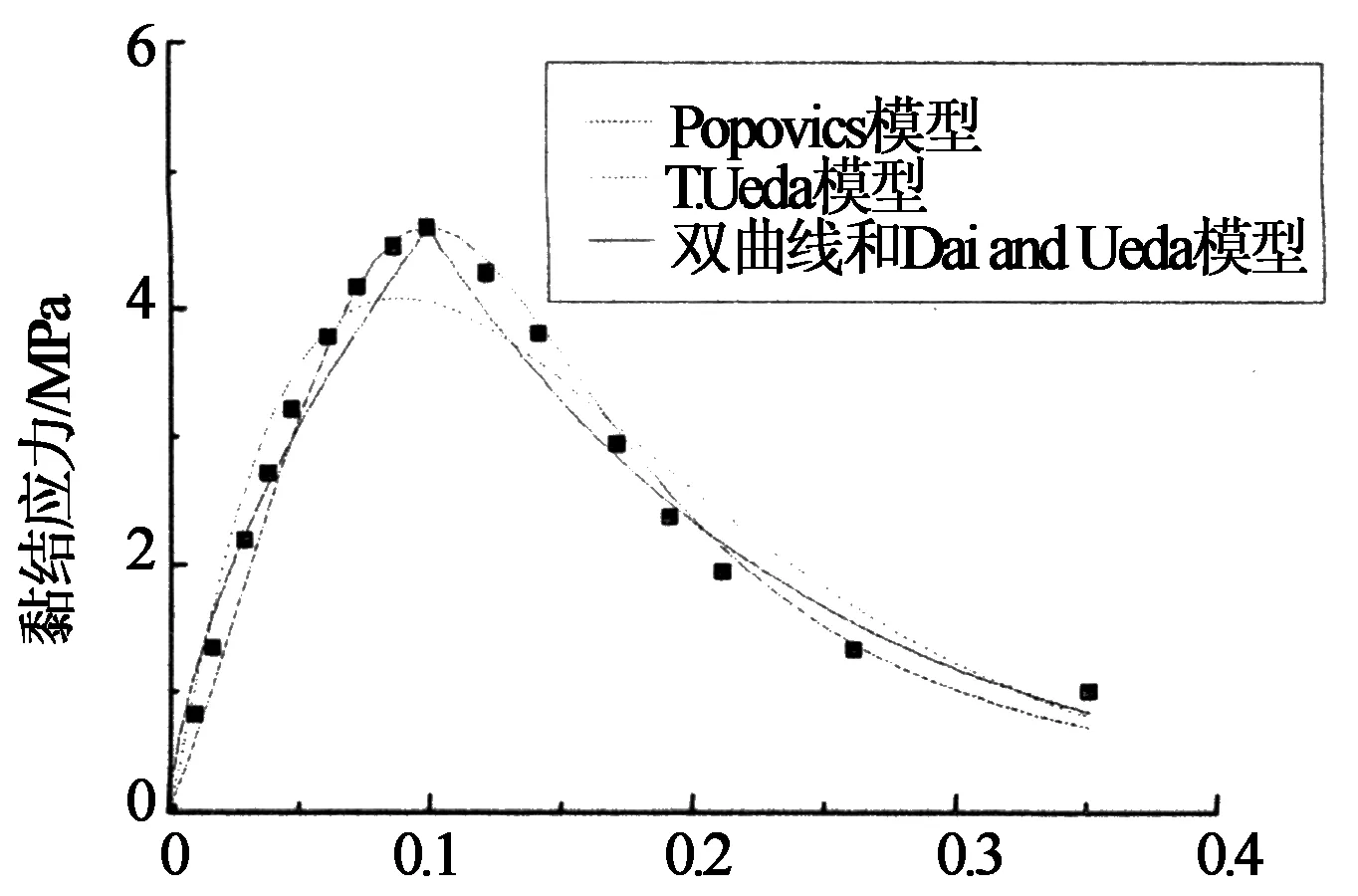
滑移量/mm

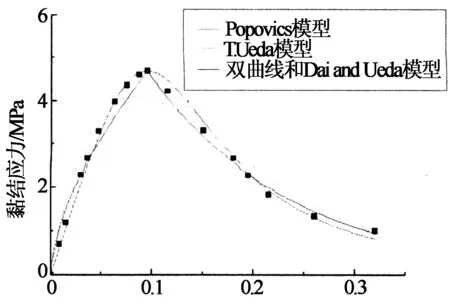
滑移量/mm

由圖可知，Popovics模型和雙曲線模型均與試驗值吻合較好，T.Ueda模型與試驗值相差較大，這是因為影響回歸分析變量的因素很多，試驗未能得到考慮多重因素影響下的回歸分析值，因而擬合曲線差異較大.但是T.Ueda模型考慮了多重因素的影響，更能夠體現界面黏結性能的復雜程度，故參考價值很大，在以后的試驗中可以依據T.Ueda模型設置多重影響因素的大量試驗，以期獲得更加正確的黏結滑移本構數學模型.

5 結 論

根據本文試驗與分析可以得到如下結論：

1)試驗獲得的黏結區域FRP應變數據表明：在界面開裂之前，不同粘貼區長度的試件在A粘貼區碳板應變分布趨勢較接近，沿板長方向大致呈指數衰減分布；而試件CF-15-1/15-2在A粘貼區10～15 cm的范圍內碳板應變基本不隨荷載變化，提供了一定的強度儲備，故其開裂荷載和極限承載力更高.當拉伸應力超過碳纖維板強度的24%時，碳板已開始從混凝土表面剝離，亦即，僅用膠粘貼碳板會過早剝落.為保證充分利用碳纖維板強度，應采用可靠錨具對碳纖維板進行錨固.

2)試驗得到的局部黏結滑移關系與典型的黏結滑移曲線關系有相同的特征，基于幾種典型的本構關系的數據回歸分析擬合，得到了符合本試驗的黏結滑移本構數學模型，Popovics模型、雙曲線模型、Dai 和Ueda模型均與試驗吻合較好，而T.Ueda模型差異較大.這些擬合的數學本構模型均能夠運用到實際工程中.但Dai和Ueda模型及T.Ueda模型均考慮了所有界面組成材料的綜合因素的影響，更能夠反映界面黏結性能的真實性，故參考價值更高，如果能夠建立考慮多重影響界面黏結性能因素的試驗組，就能夠擬合出基于這2種模型的準確模型.

[1] 鄧軍, 黃培彥. 預應力CFRP 板加固梁的界面應力分析[J].工程力學, 2009, 26(7):78-82.

DENG Jun, HUANG Pei-yan. Interfaical stress analysis of beams strengthened with a prestressed CFRP plate[J]. Engineering Mechanics, 2009, 26(7):78-88.(In Chinese)

[2] 陸新征, 滕錦光，葉列平，等. FRP加固混凝土梁受彎剝離破壞的有限元分析[J].工程力學，2006，23(6)：85-93.

LU Xin-zheng, TENG Jin-guang，YE Lie-ping,etal. Finite element analysis of intermediate crack-induced debonding in FRP strengthened RC beams[J]. Engineering Mechanics, 2006, 23(6):85-93. (In Chinese)

[3] 滕錦光, 陳建飛. FRP加固混凝土結構[M].北京: 中國建筑工業出版社, 2005:11-74.

TENG Jin-guang, CHEN Jian-fei. FRP strengthed RC structures[M]. Beijing: China Architecture & Building Press, 2005:11-74.(In Chinese)

[4] 姚諫, 滕錦光. FRP復合材料與混凝土的黏結強度試驗研究[J]. 建筑結構學報, 2003, 24(5): 10-17.

YAO Jian,TENG Jin-guang. Experiment study on bond strength between FRP and concrete[J]. Journal of Building Structures, 2003, 24(5): 10-17. (In Chinese)

[5] 彭暉,尚守平,張建仁,等. 預應力碳纖維板加固T梁的試驗與理論研究[J]. 公路交通科技, 2009, 26(10): 59-65.

PENG Hui, SHANG Shou-ping, ZHANG Jian-ren，etal. Test and theoretical research of T-beam strengthened with prestressed CFRP plate[J]. Journal of Highway and Transportation Research and Development, 2009, 26(10):59-65. (In Chinese)

[6] 彭暉,尚守平. 預應力碳纖維板加固受彎構件的試驗研究[J]. 工程力學, 2008,25(5): 142-150.

PENG Hui, SHANG Shou-ping. Experimental study of reinforced concrete beam with prestressed CFRP plate[J]. Engineering Mechanics, 2008, 25(5): 142-150. (In Chinese)

[7] BOUCHIKHI A S, LOUSDAD A, MEGUNI A. On the reduce of interfacial shear stresses in fiber reinforced polymer plate retrofitted concrete beams [J]. Materials and Design, 2010, 31(3): 1508-1515.

[8] 楊奇飛. FRP-混凝土黏結界面研究的兩個重要問題[D]. 汕頭：汕頭大學土木工程系，2009: 78-84.

YANG Qi-fei. Two important issues in FRP-concrete interfacial bond[D]. Shantou: Department of Civil Engineering, Shantou University, 2009: 78-84. (In Chinese)

[9] 葉鋒, 姚諫. 板寬對FRP-混凝土黏結界面應力影響的三維有限元分析[J]. 科技通報, 2008, 24(6):853-859.

YE Feng, YAO Jian. A 3D finite element study on the effect of FRP plate width on interfacial stress between FRP and concrete[J]. Bulletin of Science and Technology, 2008, 24(6): 853-859. (In Chinese)

[10]YUN Yan-chun, WU Yu-fei, TANG Wai-ching. Performance of FRP bonding systems under fatigue loading [J]. Engineering Structures, 2008, 30:3129-3140.

[11]陸新征, 葉列平, 滕錦光. FRP-混凝土界面黏結滑移本構模型[J]. 建筑結構學報, 2005, 26(4):10-18.

LU Xin-zheng, YE Lie-ping, TENG Jin-guang. Bond-slip model for FRP-to-concrete interface[J]. Journal of Building Structures, 2005, 26(4): 10-18. (In Chinese)

[12]李春霞, 晏石林, 周毓倩. CFRP抗彎加固混凝土梁的界面應力分析[J]. 武漢理工大學學報, 2010, 32(23):35-38.

LI Chun-xia, YAN Shi-lin, ZHOU Yu-qian.Analysis for interfacial stress in concrete beams flexural strengthened by CFRP[J]. Journal of Wuhan University of Technology, 2010, 32(23): 35-38. (In Chinese)

[13]NAKABA K, TOSHIYUKI K, TOMOKI F,etal. Bond behavior between fiber reinforced polymer laminates and concrete [J]. ACI Structural Journal, 2001, 98(3) :359 -367.

[14]UEDA T, DAI J G, SATO Y. A nonlinear bond stress-slip relationship for FRP sheet-concrete interface[C]//Proc Int Symp on Latest Achievement of Technology and Research on Retrofitting Concrete Structures. Kyoto, Japan, 2003:113 -120.

[15]LU X Z, TENG J G, YE L P,etal. Intermediate crack debonding in FRP-strengthened RC beams: FE analysis and strength model[J]. Journal of Composites for Construction, 2007, 11(S):161-174.

[16]GODAT A, LABOSSIéRE P, NEALE K W,etal. Behavior of RC members strengthened in shear with EB FRP: assessment of models and FE simulation approaches[J].Computers and Structures, 2012, 92/93: 269-282.

[17]NAKABA K, TOSHIYUKI K, TOMOKI F,etal. Bond behavior between fiber-reinforced polymer laminates and concrete[J]. ACI Structural Journal, 2001, 98(3): 359-367.

[18]MONTI M, RENZELLI M, LUCIANI P. FRP adhesion in uncracked and cracked concrete zones[C]//Proceedings of 6th International Symposium on FRP Reinforcement for Concrete Structure. Singapore: World Scientific Publications, 2003:183-192.

[19]SAVIOA M, FARRACUTI B, MAZZOTTI D. Non-linear bond-ship law for FRP-concrete interface[C]//Proceedings of 6th International Symposium on FRP Reinforcement for Concrete Structures. Singapore: World Scientific Publications, 2003:163-172.

[20]DAI J, UEDA T, SATO Y. Development of the nonlinear bond stress-slip model of fiber reinforced plastics sheet-concrete interfaces with a simple method[J]. Journal of Composites Construction, 2005, 9(1): 52-62.

[21]DSI J, UEDA T. Local bond stress relations for FRP sheets-concrete interface[C]//Proceedings of 6th Internation Symposium on FRP Reinforcement for Concrete Structures. Singapore: World Scientific Publications, 2003:143-152.