某扭轉梁后懸架側傾剛度的解算與優化*

趙 亮，晏海軍，郭孔輝,2

(1.湖南大學 汽車車身先進設計制造國家重點實驗室，湖南 長沙 410082；2.柳州孔輝汽車科技有限公司，廣西 柳州 545000)

扭轉梁式懸架是一種半獨立懸架，整個后橋由扭轉橫梁和縱向擺臂焊接而成.當汽車曲線行駛時，懸架橫梁產生扭轉，起到增加懸架側傾角剛度、減小車身傾角和提高汽車操縱穩定性的作用.

懸架的側傾角剛度是影響汽車側傾穩定性的主要因素之一[1]，直接影響到汽車操縱穩定性的一些性能指標，如不足轉向度、中性轉向側向加速度.目前工程上對扭轉梁的分析多采用生成扭轉梁模態中性文件的方法進行分析,如文獻[2-3]都是通過有限元軟件建立模態中性文件對扭轉梁懸架進行K&C分析；該方法是基于實際的物理結構,幾乎沒有進行優化的可能性,因此提出扭轉梁懸架的側傾角剛度的數值解析法.

本文根據扭轉梁式后橋的結構特點，建立了懸架的側傾力學模型，推導了帶穩定桿扭轉梁的扭轉剛度等效在車輪處的側傾角剛度的數學模型，并與虛擬樣機ADAMS仿真的結果做了對比分析.在此基礎上，進一步以扭轉橫梁和穩定桿截面尺寸參數為設計變量，采用改進的非支配排序遺傳算法(NSGA-Ⅱ)對側傾剛度及橫梁質量進行了多目標優化，一次性獲得pareto解集，通過選取合適的解，減少了懸架的非簧載質量，提高了懸架的側傾角剛度，為補償彈簧剛度的不足、提高整車平順性、降低汽車的穩態振動頻率、改善行駛特性提供了可能.對扭轉梁后橋開發初級階段總成特性參數的設計、選擇具有深刻的理論指導意義，提高了扭轉梁懸架的設計效率.

1 等效側傾角剛度的計算

懸架側傾角剛度是指汽車側傾時(車輪保持在地面上)，單位車身轉角下，懸架系統給車廂總的彈性恢復力偶矩[4].

1.1 懸架力學模型的建立

根據側傾運動的實際行駛情況，當車輪位移較小即擺臂在小角度發生擺動時，與車身的連接襯套簡化為球鉸，后橋左右輪心處承受反向的垂向力，產生對橫梁的扭矩，同時縱向擺臂與車體的鉸接點處產生垂向支反力.結合扭轉梁非獨立懸架的具體結構可畫出如圖1所示的側傾時的懸架受力圖[5].

橫梁的扭轉力矩T由兩對力偶產生，可以得到方程：

(1)

式中a為橫梁軸線到車身連接球絞中心的縱向距離；b為橫梁軸線到輪心的縱向距離.

扭矩T由橫梁的扭轉剛度k和兩端面相對扭轉角θ所得：

T=kθ

(2)

4個外力分別對懸架縱向對稱軸線取矩,有力矩平衡便可得方程：

(3)

式中c為左右輪心的距離；d為左右球絞中心的距離.

圖1 力學模型

1.2 扭轉剛度計算

在桿件兩端加上一對大小相等且反向的力矩M，如圖2所示，設兩端面的相對扭轉角為θ，將扭轉剛度定義：

(4)

橫梁扭轉剛度由兩部分提供.一部分由V型截面梁，一部分由穩定桿.下面分別對兩部分扭轉剛度進行求解.

圖2 帶穩定桿的扭轉梁示意圖

1.2.1 V型截面梁扭轉剛度計算

V型截面梁為非圓截面開口薄壁桿件，左右兩端焊接在兩縱擺臂上，因此橫梁發生扭轉時翹曲自由度受到了約束，因此只能通過約束扭轉理論來計算橫梁扭轉剛度.運用約束扭轉初參數解法求解之前，必須對約束扭轉系數k進行求解[6].

(5)

折算彈性模量：

(6)

材料的剪變模量：

(7)

截面中線長度：

s=2(pr+L)

(8)

截面的自由扭轉慣性矩：

(9)

式中l0為橫梁長；r為截面中線圓弧部分半徑；L為矩形部分長度；t為扭轉梁厚度；p為圓弧所對應的弧度；G為材料剪切模量；E為材料彈性模量；μ為泊松比；E1為折算彈性模量；JW為截面主扇性慣性矩；Jd為截面自由扭轉慣性矩.

下面用扇形面積法對JW進行求解.

由于是對稱截面，截面與對稱軸z相交于點M,將圓心o與M點分別設為參考扇性極點與參考扇性零點，如圖3所示.將M0點沿截面中線順時針旋轉α角度到達M點,該點的參考扇性面積為：

w1=αr2,0≤α≤p

(10)

M點距z軸的距離為:

y1=rsinα

(11)

圓弧部分主扇性慣性矩為：

(12)

矩形與圓弧部分的交點c沿矩形中線方向移動長度b到c1點，該點的扇性面積為：

(13)

c1點距z軸的距離為:

y2=rsinp+bsinθ

(14)

矩形部分主扇性慣性矩為：

圖3 主扇性極點求解示意圖

(15)

整個截面的主扇性慣性矩為：

Jyw=2Jyw1+2Jyw2

(16)

整個截面對z軸的慣性矩：

(17)

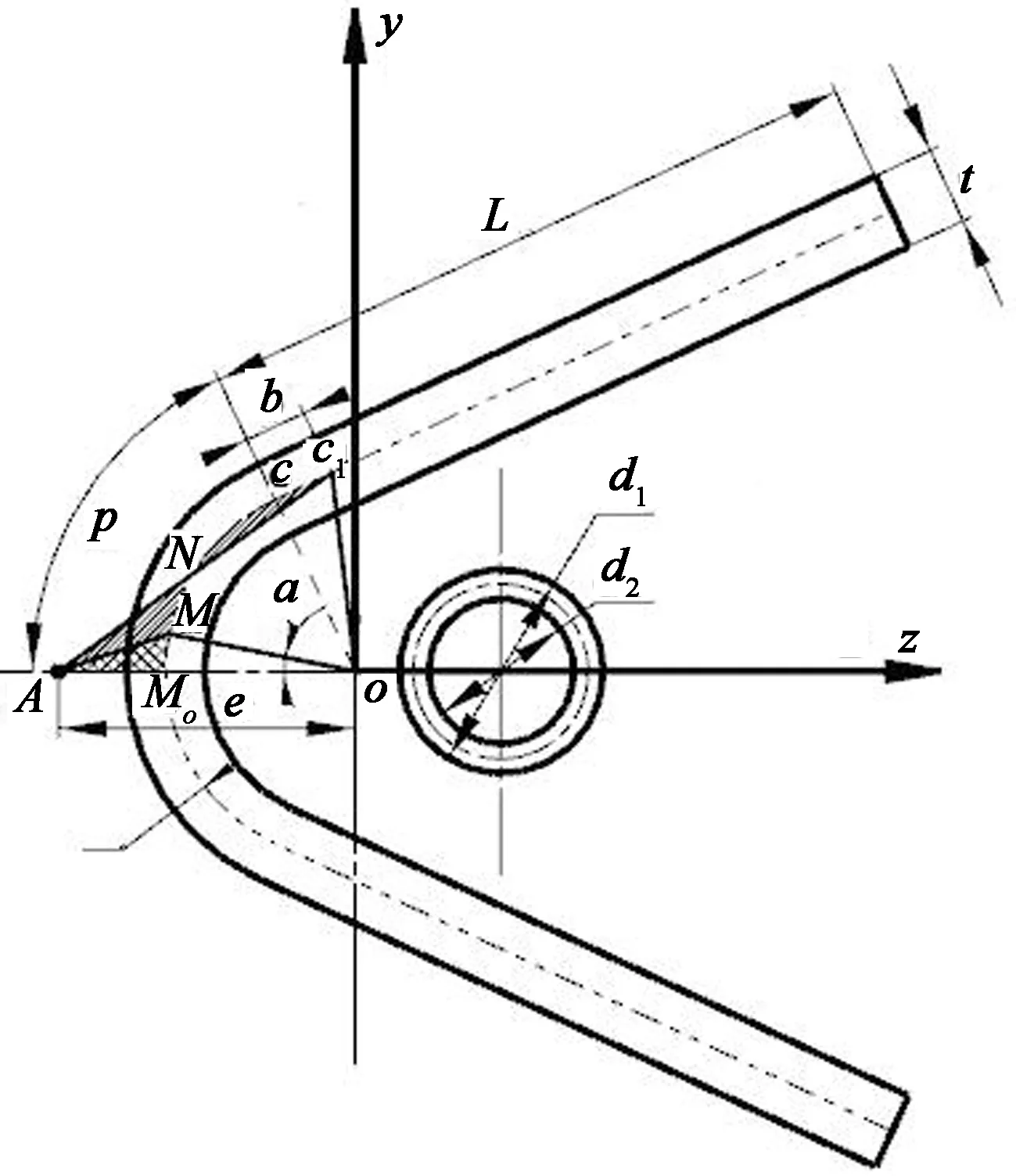
圖4 主扇性慣性矩求解示意圖

確定了主扇性的極點和零點，就可以得到M點的主扇性面積為：

(18)

則圓弧部分主扇性慣性矩為：

(19)

對矩形部分進行分析，c1點的主扇性面積為：

(20)

則2段的主扇性慣性矩為：

(21)

整個截面主扇性慣性矩為：

Jw=2Jwa+2Jwb

(22)

當x=l0時的邊界條件有

根據約束扭轉公式有：

根據第1，第2和第4個方程易解得

L0=M

在此便可以得到該薄壁橫梁的扭轉剛度:

(23)

1.2.2 扭桿扭轉剛度計算

扭桿為圓截面閉口薄壁截面，在扭轉載荷作用下不發生翹曲，其扭轉剛度可以用自由扭轉的公式計算：

(24)

整個扭轉梁的扭轉剛度為：

k=kl+kg

(25)

1.3 橫梁扭轉角

扭轉梁懸架車輪的運動可以等效為以車身連接點o1與橫梁對稱面剪切中心(上文求得的主扇性極點)o2的連線矢量t為轉軸擺動[7]，如圖5所示.右輪心與右襯套硬點坐標見表1．

圖5 等效運動學模型

表1 懸架硬點坐標

基于多體計算動力學歐拉四元素法[8]，定義：

縱向單位矢量p′=[1,0,0]T；

旋轉軸的歐拉角矢量t=[tx,ty,tz]T；

歐拉四元素矢量：

q=[λ0,λ1,λ2,λ3]T=

T=

矢量p′繞擺軸轉過β角得到矢量p=Tp′.

發生側傾運動時如圖6所示，橫梁兩端面的相對扭轉角θ定義為[9]：

(26)

1.4 側傾角剛度計算

根據定義，已知截面參數及懸架結構參數，由式(1)～(26)，設定輪跳范圍(即對應的β的范圍)，在每個分析步完成都有一個力矩和角度的變化，即可以求得側傾角剛度CK:

式中B為輪距.

圖6 橫梁扭轉角示意圖

2 數學模型驗證

考慮到襯套對扭轉剛度的影響，將擺臂與車身用球鉸鏈接，在有限元軟件ABAQUS中建立了扭轉梁式后懸架有限元仿真分析模型，如圖7所示.

圖7 ABAQUS有限元仿真模型

根據上文推導出的懸架側傾剛度計算公式，在MATLAB中編寫程序進行仿真，繪出懸架側傾剛度隨反向輪跳上下20 mm的變化曲線圖，并將其與有限元仿真的數據作對比，結果如圖8所示.

由圖8可以看出ABAQUS懸架側傾剛度曲線在小范圍內隨輪跳呈非線性變化，而理論模型側傾角剛度呈線性變化，這是由于扭轉梁懸架是一種半獨立懸架，左右輪相互產生橫向干涉，引起扭轉角非線性變化，而理論模型完全等效成拖曳臂式獨立懸架，故過程中扭轉角隨輪跳呈線性變化，所求得的曲線也呈線性變化.同時理論模型沒有考慮到擺臂的彎曲及扭轉剛度，這也導致理論值較仿真值要偏小的原因.總的來說，通過理論推導出來的側傾剛度與ABAQUS仿真值比較接近，驗證了該數學推導的正確性.

輪跳/mm

3 基于NSGA-Ⅱ算法多目標優化

NSGA-Ⅱ算法是一種基于快速分類的、采用精英策略的多目標遺傳算法.首先,隨機生成父代種群,然后對種群進行快速非勝出排序.根據每個非支配解的分級水平為指定適應值.進行選擇、復制和變異操作生成具有N個個體的子代種群,父代和子代混合利用精英策略構造出新種群,并重復循環[10].

3.1 多目標優化模型的建立

考慮到該類懸架在橫梁與縱臂焊接處往往會出現應力集中，需要通過加強板、拓撲優化等措施來改善其應力分布，而這對于數學求解應力帶來了不便.

基于上述考慮，本文以橫梁及扭桿的截面尺寸參數作為設計參數，其初始值與各變量范圍見表2，建立以桿件的質量和側傾剛度為目標函數的多目標優化數學模型如下:

s.t.xmin≤xi≤xmax

式中m為橫梁的質量,m=2(pr+L)tl0ρ,ρ為材料密度；U為輪跳過程中的平均側傾剛度；p，r，t，L，d2，d1分別代表設計變量x1，x2，x3，x4，x5，x6；l0為橫梁長.

表2 截面尺寸設計參數

3.2 優化結果與分析

采用Matlab編寫的NSGA-Ⅱ程序,應用上述數學模型,在懸架上下跳動20 mm的過程中,對兩個目標函數進行優化.在種群規模為100,交叉概率為0.9,變異概率為0.1時,進行500代進化后得到該多目標優化的Pareto最優解集,如圖9所示.

目標函數f1/kg

顯然，從圖9可以看出橫梁的質量與平均側傾剛度的倒數是一對矛盾體，往往不可能使得這兩目標同時達到最優，只能在各目標之間進行協調權衡與折中處理，盡可能滿足各目標達到最優.

為了使f1，f2盡可能最優，本文取A點.fn=(f1，f2)=(7.86,21.19)；響應的設計變量為：xn=(x1，x2，x3，x4，x5，x6)=(62.86，18.38，4，70，15.25，23).

對比優化前后目標函數的值，優化后帶穩定桿的橫梁總質量減少了10.95%，同時側傾角剛度增加了10.77%，可以得出優化效果比較理想，為扭轉梁開發提供了設計空間.

4 結 論

建立了帶橫向穩定桿的扭轉梁截面參數與其等效在車輪處側傾角剛度之間的數學模型，與虛擬樣機ADAMS仿真的結果保持較高的一致性，驗證了模型的正確性.基于該模型，采用改進的非支配排序遺傳算法(NSGA-Ⅱ)對側傾剛度和橫梁的質量進行了多目標優化，獲得pareto解，結果表明該優化方法是可行的.為補償彈簧側傾剛度的不足，提高整車平順性能提供了可能[11].對扭轉梁懸架設計初級階段總成特性參數的設計、選擇具有深刻的理論指導意義，提高了扭轉梁懸架的設計效率.

[1]WINKLER C B,KARAMIHAS S M,BOGARD S E.Roll stability performance of heavy-vehicle suspensions[J].SAE Paper， 922426.

[2]CHOI B L,CHOI D H,MIN J,etal.Torsion beam axle system design with a multidisciplinary approach[J].International Journal of Automotive Technology,2009,10(1)：49-54.

[3]劉興乾.扭轉梁與四連桿懸架k&c特性分析及評價[D].長春：吉林大學汽車工程學院,2008.

LIU Xing-qian.The simulation analysis and evaluation for k&c characters of beam-twist and multi-link suspension[D].Changchun:College of Automotive Engineering,Jilin University,2008.(In Chinese)

[4]余志生,汽車理論[M].北京：機械工業出版社,2009:164-167.

YU Zhi-sheng.Theory of automobile[M].Beijing: China Machine Press,2009:164-167.(In Chinese)

[5]陳棟華,靳曉雄,黃海波,等.轎車扭桿式半獨立后懸架動力學仿真和試驗研究[J].汽車工程,2007,29(2):149-152.

CHEN Dong-hua,JIN Xiao-xiong,HUANG Hai-bo,etal.Dynamics simulation and experimental study on torsion bar rear suspension of passenger car[J].Automotive Engineering,2007,29(2):149-152.(In Chinese)

[6]包世華,周堅.薄壁桿件結構力學[M].北京:中國建筑工業出版社,1991:38-72.

BAO Shi-hua,ZHOU Jian.Structural mechanics of thin-walled bar[M].Beijing:China Architecture and Building Press,1991:38-72.(In Chinese)

[7]耶爾森·賴姆帕爾.汽車底盤基礎[M].北京：科學普及出版社,1992:126,176.

YALE'S Lai Mparr.The automotive chassis engineering principles[M].Beijing:Popular Science Press,1992:126,176.(In Chinese)

[8]洪嘉振.計算多體系統動力學[M].北京：高等教育出版社,1999:37,49.

HONG Jia-zhen.Computational multibody system dynamics[M].Beijing: Higher Education Press,1999:37,49.(In Chinese)

[9]MUN K J,KIM T J,KIM Y S.Analysis of the roll properties of a tubular-type torsion beam suspension [J].Journal of Automobile Engineering,2010,224(1):1-13.

[10]DEB K，PRATA P A，AGARWAL S,etal.A fast and elitist multiobjective genetic algorithm: NSGA-II[J].IEEE Transactions on Evolutionary Computation,2002(6):182-197.

[11]王望予.汽車設計[M].北京:機械工業出版社,2000:202- 205.

WANG Wang-yu.Automobile design[M].Beijing: China Machine Press,2000:202-205.(In Chinese)