某型包裝機推手機構剛柔耦合系統動力學研究*

周長江，胡 波，祝智斌

(1.湖南大學 國家高效磨削工程技術研究中心，湖南 長沙 410082；2.湖南大學 機械與運載工程學院，湖南 長沙 410082;3.中煙機械集團常德煙草機械有限責任公司，湖南 常德 415000)

隨著包裝機械輕質、高速、高精度化發展，柔性構件變形引起的運動誤差不能忽略.基于多剛體動力學理論建立的計算模型，在分析柔性構件變形對機械系統運動精度的影響時存在一定的不足[1-2].針對上述問題，研究者提出剛柔體耦合動力學建模.Winfry R C[3]將多剛體動力學與結構動力學進行疊加，提出運動—彈性動力學分析方法.Likins P W[4]和Kane T R 等[5]提出了混合坐標建模方法，并以高速旋轉的懸臂梁為例，證明零次近似耦合模型存在“動力剛化”現象.劉錦陽[6]、楊輝等[7]通過縱橫振動的二次耦合變形量，研究了“動力剛化”問題，并用實驗證明該模型的有效性.朱才朝[8]、張立軍等[9]基于剛柔耦合系統動力學理論，研究了柔性車架對汽車平順性的影響.在包裝機械方面，田曉鴻[10]、韓炬等[11]分別對包裝機和熱封機構進行了多剛體運動學建模與仿真分析.綜上所述，若對高速運動的輕質柔性構件作剛體假設，基于多剛體動力學理論的計算結果將存在一定誤差.應用機構動力學方法計算出載荷邊界，再由結構動力學方法計算出該機構在此載荷邊界下的應力與變形.機構動力學求出的動態載荷，作為載荷邊界條件直接施加在有限元計算模型上則比較困難.若柔性桿件運動軌跡不規則且變形較大，在有限元計算模型上直接定義該類位移約束條件亦較困難.若簡化為靜態約束，則仿真條件與實際工況有出入，會影響計算結果的精度.

本文以某型高速包裝機(1 000包/min)的柔性推手機構為研究對象，基于剛柔耦合系統動力學理論，重點研究柔性構件長臂推手的動態應力及運動軌跡.基于剛柔耦合系統動力學模型和有限元分析模型，對比研究長臂推手工作點應力的計算值；基于多剛體動力學模型和剛柔耦合系統動力學模型，對比研究構件柔性化對系統運動軌跡精度的影響.

1 剛柔耦合系統動力學計算原理

將包裝機推手機構中剛度較大的零部件按多剛體系統動力學建立方程，柔度較大的零件由有限元方法和模態綜合疊加法建立方程，兩者組集可得剛柔耦合系統的動力學方程[12-13].

柔性體坐標系如圖1所示.其中，er為慣性坐標系，eb為建立在柔性體上的動坐標系，eb在er中的坐標為參考坐標.

小變形的柔體運動可分解為剛性運動與彈性變形.對于柔性體上一點P，其位置矢量表示為：

r=r0+A(rp+up)

(1)

式中r為P點在慣性坐標系er中的位置矢量；r0為動坐標系eb原點在er中的位置矢量；A為動坐標系相對慣性坐標系的方向余弦矩陣；r0為動坐標系eb原點在er中的位置矢量；up為點P的變形量，up=Φpqf；Φp為點P滿足里茲基矢量假設的變形模態矩陣；qf為變形的廣義坐標．

圖1 柔性體坐標描述

由拉格朗日方程導出柔性體的運動方程：

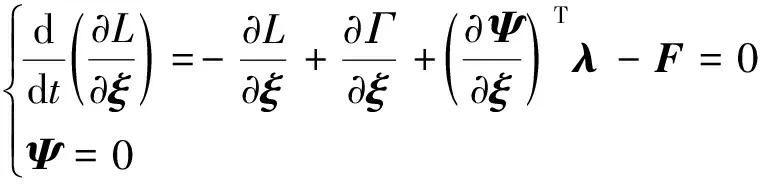
(2)

式中ξ=(xyzψθFa1Fa2…Fam)T；Ψ為約束方程；λ為對應約束方程的拉氏乘子；ξ為廣義坐標；Fai為投影到ξ上的廣義力，i=1，2，…，m；F為作用在物體上的廣義慣性力；L為拉格朗日項，L=T-V，T，V為系統動能和勢能；Γ為系統能量損耗函數；θ為模態坐標．

將計算出的系統動能T、勢能V、能量損耗函數Γ代入式(2)，得出柔性體的運動微分方程

(3)

式中m為柔性體的質量矩陣；k為對應模態坐標θ的廣義剛度矩陣；Fg為重力；D為包含阻尼系數的常值對稱矩陣．

2 推手機構剛柔耦合系統動力學建模

包裝機推手機構的長臂推手為細長件，即柔性較大.工作時桿件變形對運動軌跡精度可能產生一定的影響，有必要研究其受力狀態.將長臂推手作為柔性體，建立推手機構的動力學模型更接近實際運動.基于剛柔耦合系統動力學，可較方便地計算長臂推手的動態應力.該方法可較好地解決在有限元模型上直接添加不規則動態載荷邊界及位移約束的困難，定義的仿真條件更符合實際工況.

基于ANSYS和ADAMS軟件平臺，運用有限元方法和模態綜合疊加法，將長臂推手柔性化，建立剛柔耦合系統動力學模型.柔性體建模關鍵在于建立剛性區域和外聯點.剛性區域是柔體上與剛體鉸接耦合的不變形區域；外聯點即為位于剛柔耦合處的無質量點單元，用來建立柔性體約束的參考坐標.剛性區域和外聯點如圖2所示.

圖2 柔性長臂推手剛性區域和外聯點

模態階數及模態頻率范圍關系到模態綜合疊加法計算結果的準確性，理論上模態頻率階數與計算結果準確性正相關.考慮計算效率，提取長臂推手柔性模型前100階自由模態，計入模態綜合疊加法.在外聯點上添加剛體與柔體間的約束，建立剛柔耦合系統動力學模型，見圖3.

圖3 推手機構剛柔耦合系統動力學模型

圖3中長臂推手轉速為500 r/min，剛度較小.高速狀態下，作為純剛體進行仿真計算，動力學性能與實際相差可能較大.柔性化長臂推手，將其作為主要研究對象.

3 推手機構剛柔耦合系統的動態特性

3.1 長臂推手動態應力計算

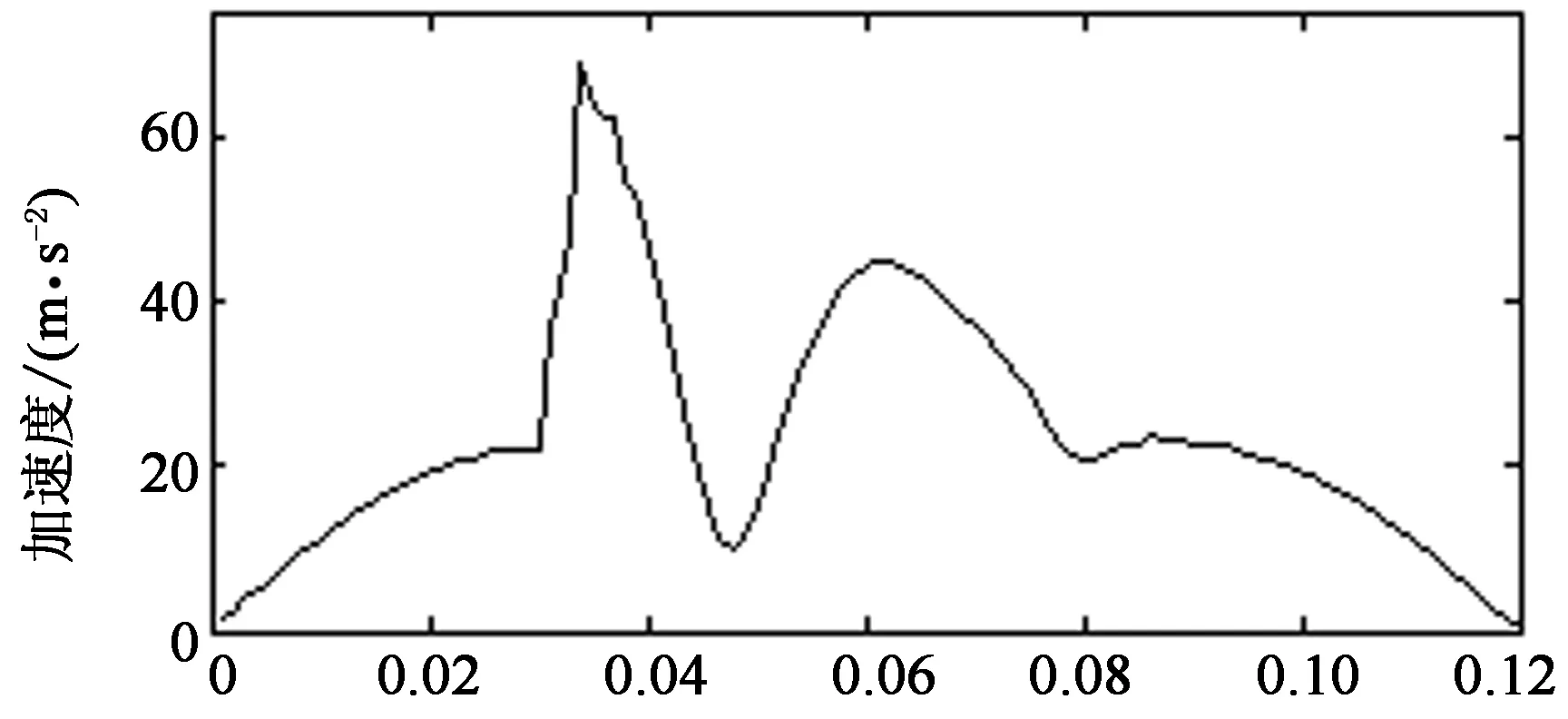
設定電機運轉速度500 r/min，根據機構運動關系，計算出測量點的加速度，見圖4.

t/s

機構的運轉周期為0.12 s，0～0.03 s及0.09～0.12 s為工作段，0.03～0.09 s為回程階段.基于剛柔耦合系統動力學模型，計算柔性推手整個周期的應力.提取前10個較大應力值及其節點位置，見表1.

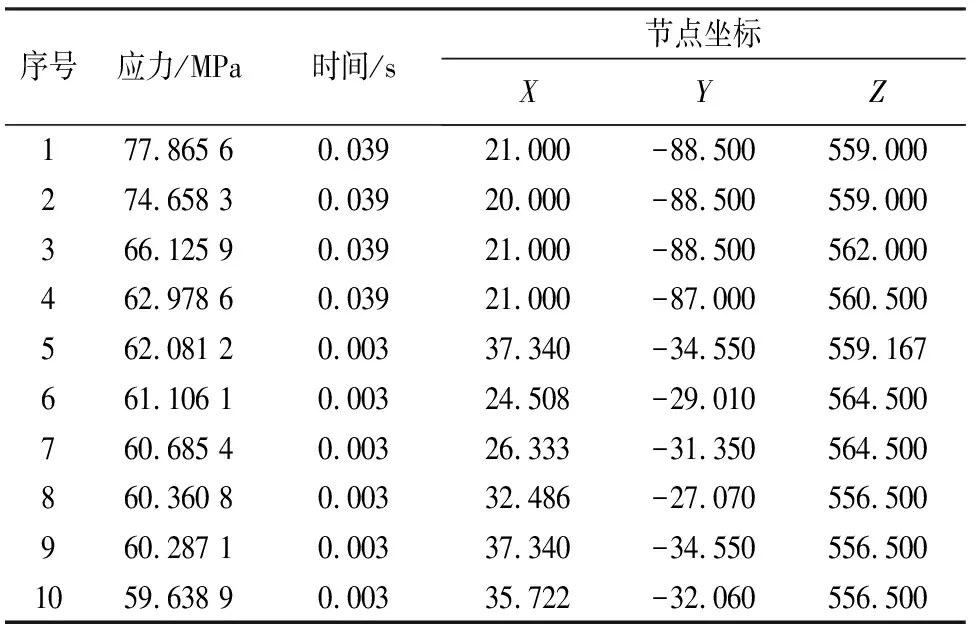
表1 前10大動態應力值

動態應力最大值為77.865 6 MPa，小于材料的許用應力[σ]=210 MPa，即滿足強度要求.由表1可知應力較大值主要集中在t=0.003 s與t=0.039 s時刻.主要原因是：在0.003 s時，推手機構快速啟動，加速度較大；在0.039 s時，推手機構的加速度達到峰值(見圖4)，即引起了較大的動載荷.圖5、圖6分別為該兩時刻柔性長臂推手的應力云圖.

基于有限元分析模型，求解長臂推手的應力狀態.與剛柔耦合系統動力學模型的計算結果比較，驗證動態計算結果的正確性.基于多剛體動力學理論，得到長臂推手在0.003 s和0.039 s的受力狀態，見表2．

圖5 t=0.003 s長臂推手的動態應力

圖6 t=0.039 s長臂推手的動態應力

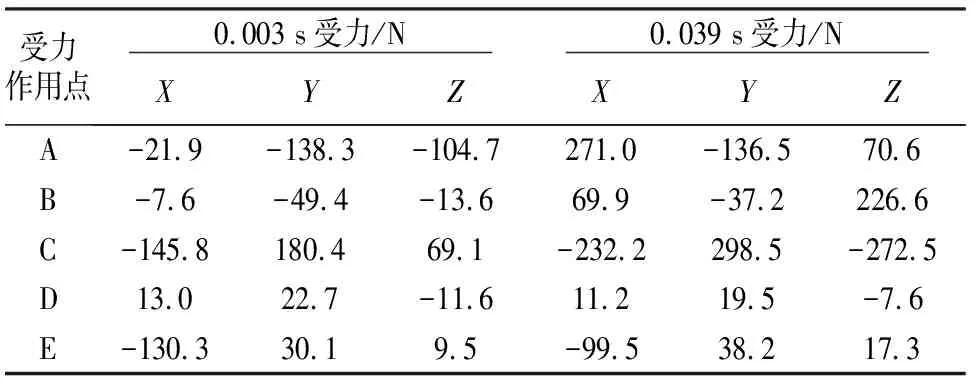
表2 0.003 s和0.039 s時刻長臂推手的受力狀態

其中A，B，C為長臂推手三處鉸鏈受力作用點，D，E為推板在運動過程中對長臂推手作用力點.在ABAQUS中建立長臂推手的有限元分析模型，將表2中的受力狀態作為邊界條件，計算長臂推手的準動態應力.應力云圖分別見圖7和圖8.

圖7 t=0.003 s長臂推手的準動態應力

圖8 t=0.039 s長臂推手的準動態應力

兩種計算方法的最大應力值如表3所示．

表3 動態應力與準動態應力最大值

由表3可知，動態應力最大值略大于準動態應力最大值.其原因為：基于剛柔耦合系統動力學的計算模型，定義了不規則運動約束，各單元自身質量產生慣性力，加大了長臂推手的內部應力.該計算模型的工況與實際工況比較相符，計算結果較好.

3.2 柔體變形對運動的影響

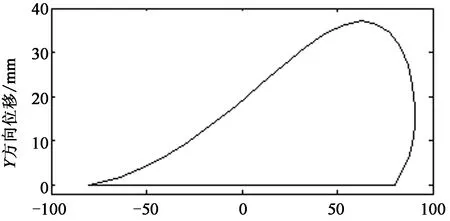
接觸推包時，長臂推手加速度較大.為避免產生較大的接觸力損壞產品，長臂推手選用柔度較大的輕質鋁合金.鋁合金在高速運行且加速度較大時，柔度引起的變形會導致一定的運動誤差值.長臂推手在圖3所示的XOY平面內運動，直線段為工作推程，曲線段為回程避讓.運動較為復雜，其運動軌跡見圖9.

X方向位移/mm

建立推手機構的剛柔耦合系統模型和多剛體系統模型，研究柔性推手變形對運動軌跡的影響.在相同工況下，對兩種模型進行動力學仿真.對比長臂推手的運動軌跡，分析柔性推手變形引起的運動誤差.圖10為柔性推手變形引起的運動軌跡變化量.

t/s

柔性推手變形會引起運動軌跡的偏移.圖10表明，該型包裝機在高速狀態下，基于多剛體動力學模型的計算結果存在一定誤差.長臂推手在XOY平面內的運動，X,Y方向受力較大.柔性推手的變形主要表現為X,Y方向，即該兩方向的運動軌跡變化量較大，見表4.

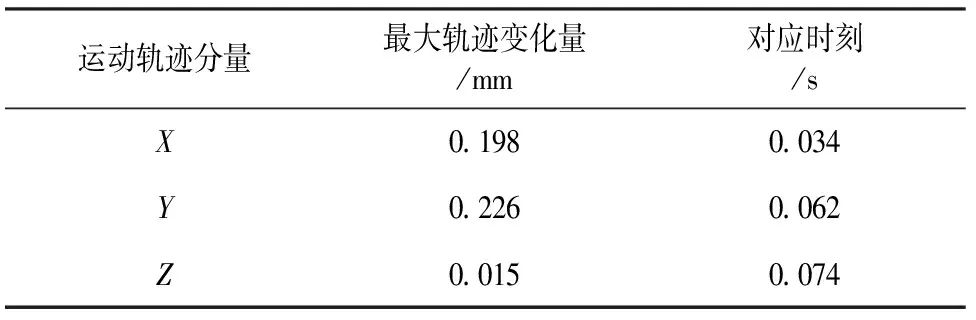
表4 運動軌跡的最大相對變化量

由圖10及表4可知，柔性推手變形引起的軌跡偏差，主要發生在推手機構的回程階段，即對應時間段0.03～0.09 s.該階段對包裝質量的影響較小，但對結構性能和運動穩定性會產生一定的影響.

4 結 論

1)基于剛柔耦合系統動力學模型與有限元分析模型，對比研究長臂推手的計算應力，驗證了基于剛柔耦合系統動力學理論計算動態應力方法的正確性.

2)基于剛柔耦合系統動力學理論與多剛體動力學理論，對比分析長臂推手測量點的運動軌跡，研究表明該型包裝機在高速狀態下基于剛柔耦合系統動力學模型的計算結果更為準確.

[1]趙陽,范菊.多剛體動力學在纜索動力分析中的應用[J].船海工程,2011,40(1):152-155．

ZHAO Yang,FAN Ju.Application of the multi-body system dynamics in the dynamic analysis of mooring lines [J].Ship & Ocean Engineering,2011,40(1): 152-155．(In Chinese)

[2]王其東,秦煒華.基于多剛體動力學和規則協調的汽車EPS與ASS建模與控制[J].中國機械工程,2010,21(14): 1709-1713．

WANG Qi-dong,QIN Wei-hua.Modeling and control of vehicle electric power steering and active suspension system based on multi-body dynamics and rule-based coordination[J].Chinese Journal of Mechanical Engineering,2010,21(14):1709-1713．(In Chinese)

[3]WINFRY R C.Elastic link mechanism dynamics [J].ASME Journal of Engineering for Industry,1971,93 (1):268-272.

[4]LIKINS P W.Finite element appendage equations for hybrid coordinate dynamic analysis[J].Journal of Solids & Structure,1972,8(5):709-731.

[5]KANE T R,LEVINSON D A.Formulation of equation of motion for complex spacecraft [J].Journal of Guidance,Control and Dynamics,1980,3(2):99-112.

[6]劉錦陽,洪嘉振.剛-柔耦合動力學系統的建模理論研究[J].力學學報,2002,34(3):408-415.

LIU Jing-yang,HONG Jia-zhen.Study on dynamic modeling theory of rigid-flexible coupling systems[J]． Acta Mechanica Sinica,2002,34(3):408-415．(In Chinese)

[7]楊輝,洪嘉振.柔性多體系統動力學實驗研究綜述[J].力學進展,2004,24(2):171-181.

YANG Hui,HONG Jia-zhen.Survey of experiments for dynamics of flexible multi body system[J].Advances in Mechanics,2004,24(2):171-181．(In Chinese)

[8]朱才朝，唐倩.人-機-路環境下摩托車剛柔耦合系統動力學研究[J].機械工程學報,2009,45(5):225-229.

ZHU Cai-chao,TANG Qian.Dynamic study for driver-motorcycle-road system with rigid-flexible coupling [J].Journal of Mechanical Engineering,2009,45(5):225-229．(In Chinese)

[9]張立軍,張宇.基于懸架剛柔耦合模型的汽車平順性[J].農業機械學報,2008,39(8):28-32．

ZHANG Li-jun,ZHANG Yu.Ride comfort based on the rigid-flexible coupling model of suspension[J].Transactions of the Chinese Society for Agricultural Machinery,2008,39(8): 28-32．(In Chinese)

[10]田曉鴻,李龍.某包裝機推手裝置的運動仿真分析[J].包裝與食品機械，2011,29(4):35-37．

TIAN Xiao-hong,LI Long.Analysis of the simulation movement in cigarette pusher device [J].Journal of Packaging and Food Machinery,2011,29(4):35-37．(In Chinese)

[11]韓炬,王瑩.包裝機熱封機構的建模及動力學分析[J].食品與機械，2013,29(1):146-148．

HAN Jun,WANG Ying.Modeling and dynamics simulation analysis for heat sealing mechanism of packaging machine [J].Journal of Food and Machinery,2013,29(1):146-148．(In Chinese)

[12]LIMEBEER D J,SHARP R S,EVANGELOU S.Motorcycle steering oscillations due to road profiling [J].Journal of Applied Mechanics,2002,69 (6):724-739.

[13]BASILEIOS M,PETER E.Analysis of alternative front suspension system for motorcycles[J].Vehicle System Dynamics,2006,44(Sup):679-689.