彈性地基復(fù)合曲梁抗彎力學性能研究
郝扣安, 王振清, 周利民, 王欣
(1.哈爾濱工程大學 航天與建筑工程學院,黑龍江 哈爾濱 150001;2.香港理工大學 機械工程系,香港;3. 上海宇航系統(tǒng)工程研究所,上海 201109)
復(fù)合材料憑借其優(yōu)越的使用性能、結(jié)構(gòu)和功能的可設(shè)計性,成為航空航天、汽車、船舶等眾多產(chǎn)業(yè)的首選材料之一。實際工程結(jié)構(gòu)中,對曲面結(jié)構(gòu)復(fù)合材料的需求是不可避免的,如倒角、對T型連接的加固等等。截至目前,針對彎曲結(jié)構(gòu)梁的研究還大多集中于實驗[1]和數(shù)值分析[2]。其中,Pagano[3-4]利用線彈性理論研究了多層復(fù)合材料層合板,并給出了在承受柱形彎曲狀態(tài)下的精確解。然而,他考慮的是平板復(fù)合材料層合板承受橫向載荷的情況。Lekhnitskii[5]給出了各向異性彎曲梁在力矩載荷下的通解。該方法同樣也為ASTMD6415[6]采納用于計算彎曲梁四點彎曲實驗中層間拉伸應(yīng)力。Shenoi[7]和李永勝[8]建立了基于彈性體彎曲梁彎曲行為的模型,得到了各向異性梁的彈性解。高階剪切變形理論[9-10]可對跨厚比大于4的板殼結(jié)構(gòu),精確的計算面內(nèi)變形和應(yīng)力,但無法計算復(fù)合材料板殼的層間應(yīng)力。
本文通過給定適當?shù)倪吔鐥l件和位移應(yīng)力協(xié)調(diào)方程,利用彈性地基作用下的曲梁應(yīng)力解,確定了平面內(nèi)正應(yīng)力中性軸的位置,推導(dǎo)出由2種不同材料組成的層合曲梁應(yīng)力解。計算了不同幾何外形、不同材料比例和材料參數(shù)對于曲梁層間正應(yīng)力和平面內(nèi)正應(yīng)力大小、鋪層順序的影響。
1 曲梁的彈性基礎(chǔ)模型
1.1 基本方程
李永勝等[8]考慮了彈性地基作用下的曲梁抗彎性能,如圖1所示,單位寬度的曲梁被放置于模量為E的彈性地基上。其中,曲梁的內(nèi)徑為Ri,外徑為Ro。假設(shè)彈性地基的反作用力垂直于曲梁表面,且與曲梁每點處的撓度v成正比。
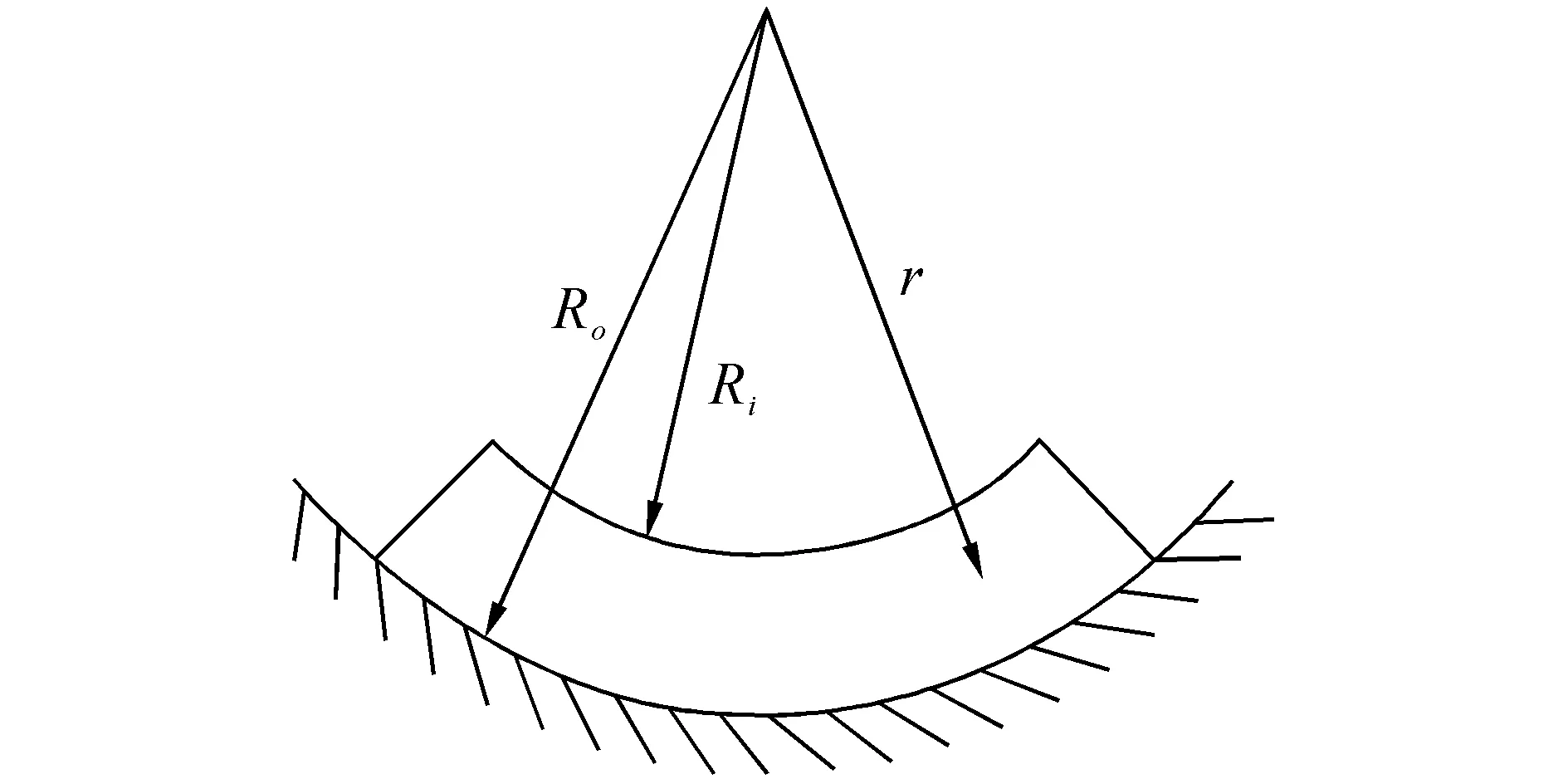
(a) 幾何外形
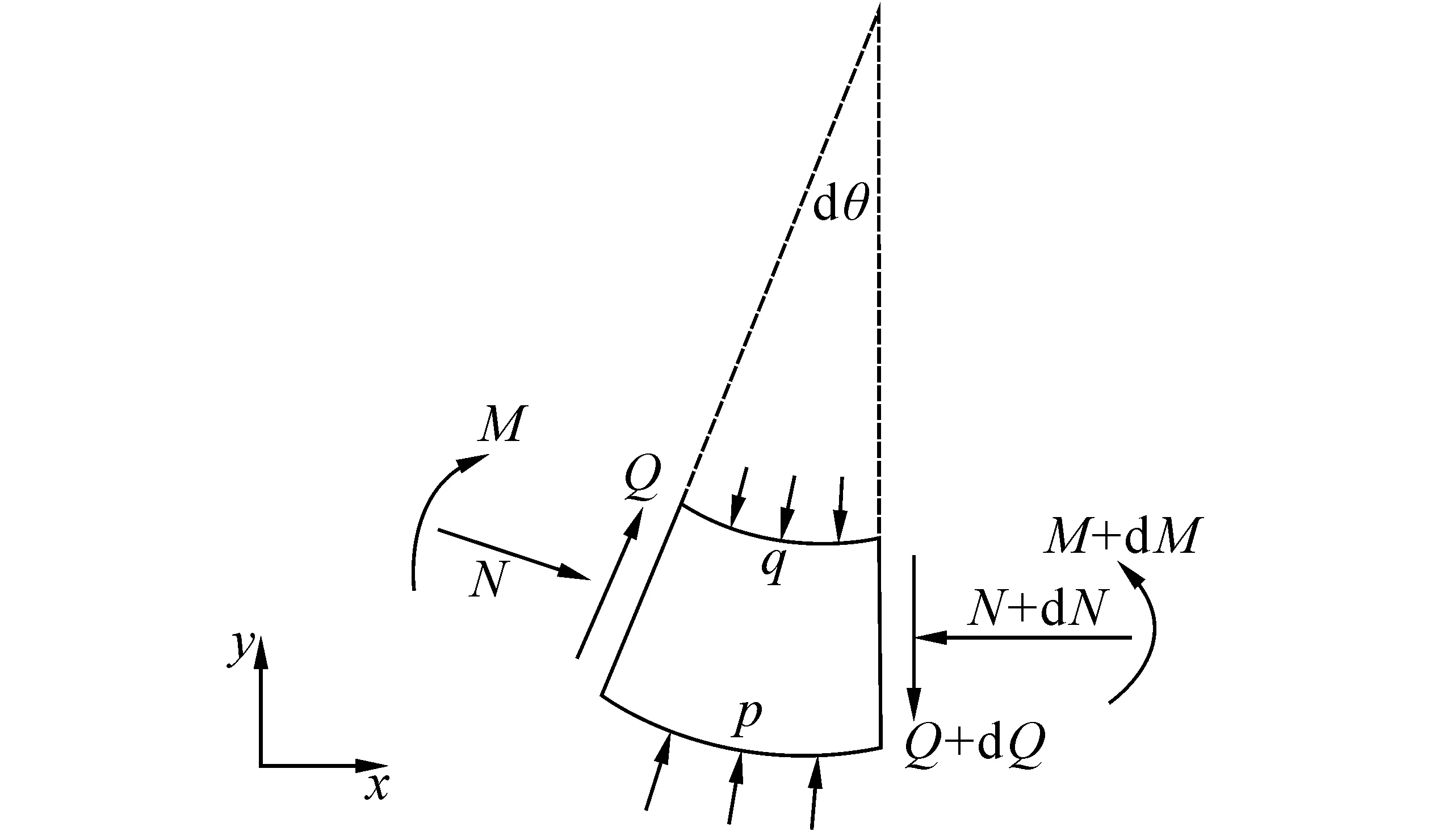
(b) 單元受力情況
(1)
曲梁的平衡方程有[7]:
(2)
為求解上式微分方程,需要建立力矩Mx與曲率變化κx的關(guān)系。對于復(fù)合材料層合板,二者的關(guān)系可由經(jīng)典層合板理論[11]得出:
(3)
式中,
式中:Aij為拉伸剛度,Bij為拉彎耦合剛度,Dij為彎曲剛度,ε0為層合板幾何中心處的應(yīng)變,κ為曲梁的曲率變化。對于彎曲結(jié)構(gòu)來說,力矩Mx與曲率變化κx的表達式需要考慮拉彎耦合、彎扭耦合。
僅考慮x方向的曲率變化,由式(3)可得:
(4)
(5)
純彎曲載荷下,應(yīng)力分量與θ角度無關(guān),且有τrθ=0。
對于各向異性材料,有協(xié)調(diào)方程[13]:
(6)
求得應(yīng)力分量:
(7)
式中:λ=Eθ/Er,為材料的周向與徑向彈性模量之比;C2、C3和C4為常數(shù),可通過給定邊界條件求得。
1.2 邊界條件
由圖1(b),有邊界條件:
(8)
將式(7)中的各應(yīng)力分量代入邊界條件,式(8)中第3式可自動滿足,可求得C2、C3和C4,故可求得應(yīng)力分量表達式[7]:
(9)
2 基于彈性地基的復(fù)合曲梁模型
2.1 基本假設(shè)
在對復(fù)合曲梁分析之前,給出幾點假設(shè):
1)復(fù)合曲梁是由線彈性或各向異性材料組成,其材料主軸方向與整體坐標系方向一致;
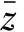
3)不考慮自由邊界效應(yīng) (Free-edge effects);
4)彎曲梁中心線處的半徑與彎曲梁厚度之比RG/t皆足夠大以保證應(yīng)變得以線性分布。
2.2 中性軸位置的確定
本文討論矩形截面的復(fù)合曲梁,該復(fù)合曲梁(見圖2),由兩種材料組成。圖2同時還給出了復(fù)合材料橫截面的幾何參數(shù),靠近外徑部分為第一種材料,用I表示;靠近內(nèi)徑處的第2種材料,用II表示。復(fù)合曲梁的厚度為t,其中I層材料的厚度為tI,II層材料的厚度為tII。
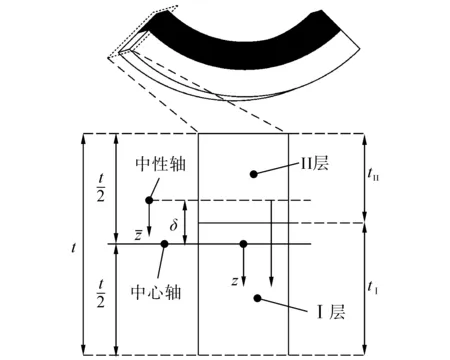
圖2 復(fù)合曲梁橫截面尺寸
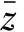
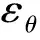
(10)
式中:r′為受到外力載荷后該點處的半徑,δ為中心軸與中性軸之間的距離。
由正向力N與彎曲力矩M所產(chǎn)生的正應(yīng)力施加于中心軸z軸處,可得平衡方程如下:
(11)
復(fù)合曲梁由兩部分組成,I層曲梁和II層曲梁。結(jié)合式(10),對式(11)進行變量替換,得:
(12)
由此可得:
(13)
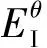
聯(lián)立式(13)中兩個方程,求得
(14)
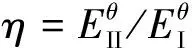
2.3 復(fù)合曲梁應(yīng)力求解
對于平面各向異性材料平面應(yīng)變問題而言,Hooke's定律表達為[14]:
(15)
考慮極坐標中的幾何方程:
(16)
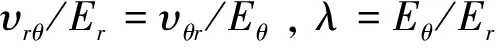
(17)
(18)
(19)
同時,考慮邊界處徑向、周向位移連續(xù),有邊界條件如下:
(20)
因此,結(jié)合邊界條件式(18)~(20),可求得復(fù)合曲梁厚度方向的層間正應(yīng)力與平面內(nèi)正應(yīng)力。
3 討論與分析
3.1 內(nèi)外徑之比對曲梁應(yīng)力的影響
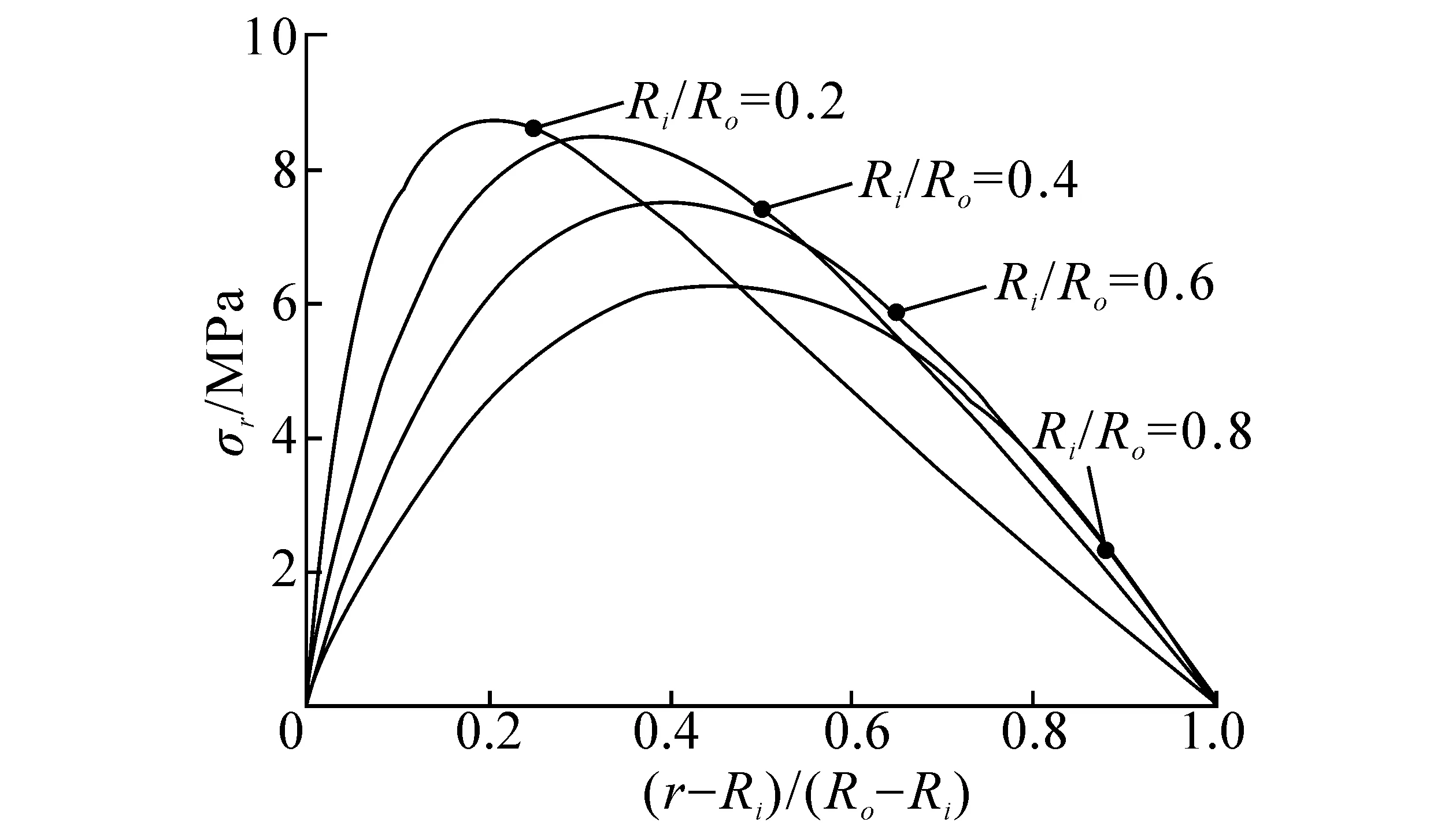
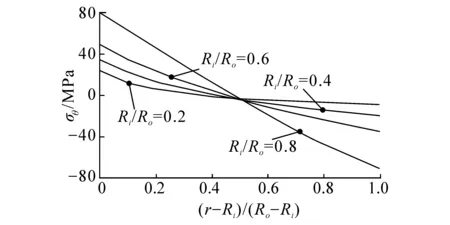
針對單一材料的彎曲梁結(jié)構(gòu),根據(jù)式(9)考察內(nèi)外徑之比(Ri/Ro)對于層間正應(yīng)力與平面內(nèi)正應(yīng)力的分布的影響。如果內(nèi)徑Ri=6.4 mm,M=1 000 N·m,圖3分別給出了Ri/Ro= 0.2、0.4、0.6、0.8曲梁應(yīng)力分布情況,圖中對橫坐標進行無量綱處理,為(r-Ri)/(Ro-Ri)。
(a) 層間正應(yīng)力分布
(b) 平面內(nèi)正應(yīng)力分布
觀察圖3(a)發(fā)現(xiàn),4條曲線的層間正應(yīng)力最大值都位于偏離幾何中心軸靠近內(nèi)徑處,而內(nèi)外徑之比不僅影響彎曲梁層間最大正應(yīng)力值的大小,對于層間最大正應(yīng)力值的相對位置也有影響。隨著Ri/Ro的升高,層間最大正應(yīng)力值降低,同時其位置逐漸向幾何中心軸靠近。由圖3(b)可知,隨著Ri/Ro的升高,平面內(nèi)最大正應(yīng)力值也升高,而平面內(nèi)正應(yīng)力中性軸相對位置幾乎不變。周向徑向彈性模量之比λ對于應(yīng)力分布無明顯影響[7]。
3.2 材料參數(shù)對中性軸位置的影響
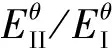
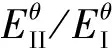
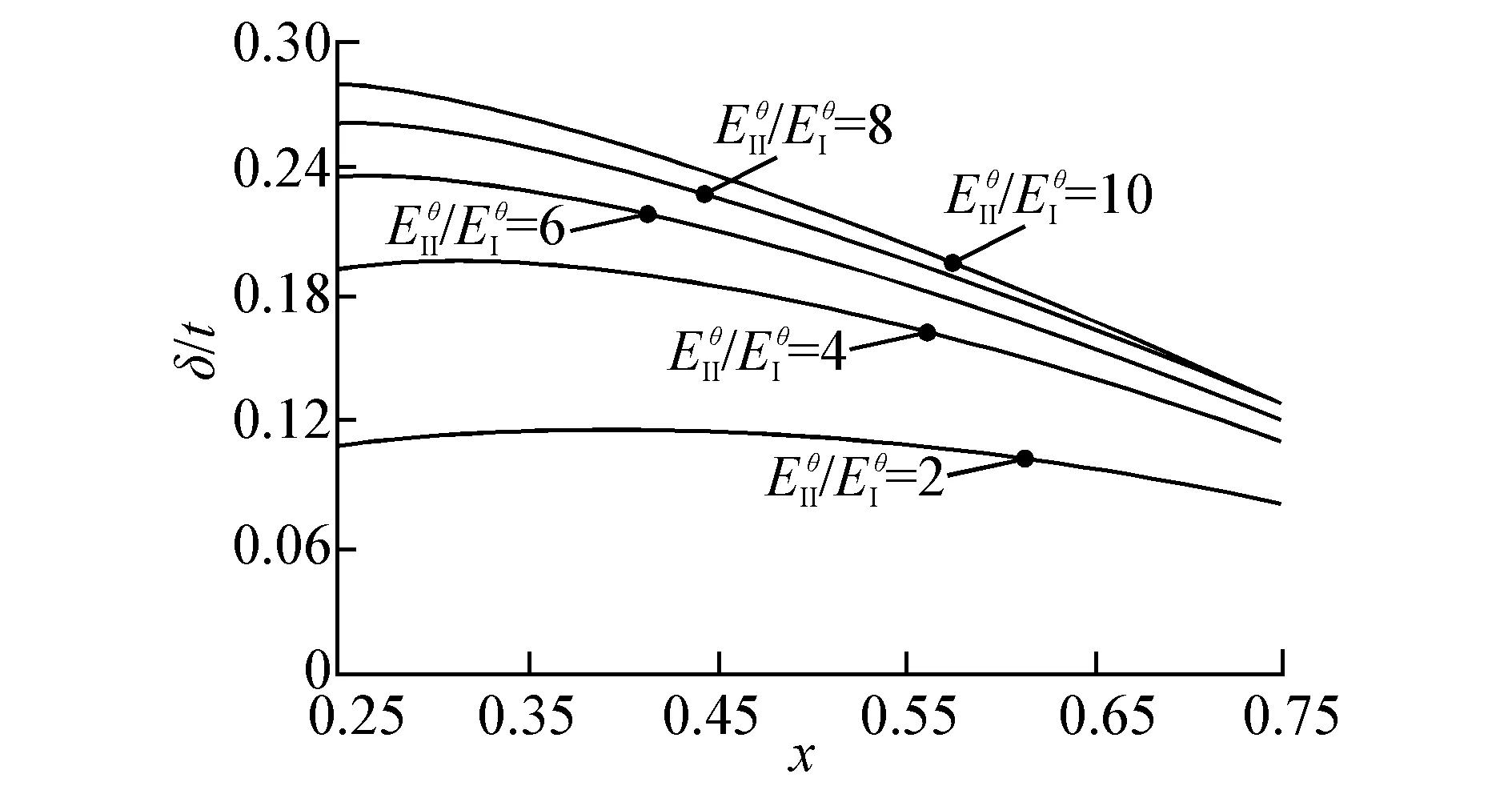
圖4 不同周向模量比的中性軸位置隨χ的變化情況
3.3 材料參數(shù)、體積比對復(fù)合曲梁應(yīng)力的影響
針對材料II,考慮其體積含量對曲梁應(yīng)力的影響,其中VII為材料II在曲梁結(jié)構(gòu)中的體積百分比。
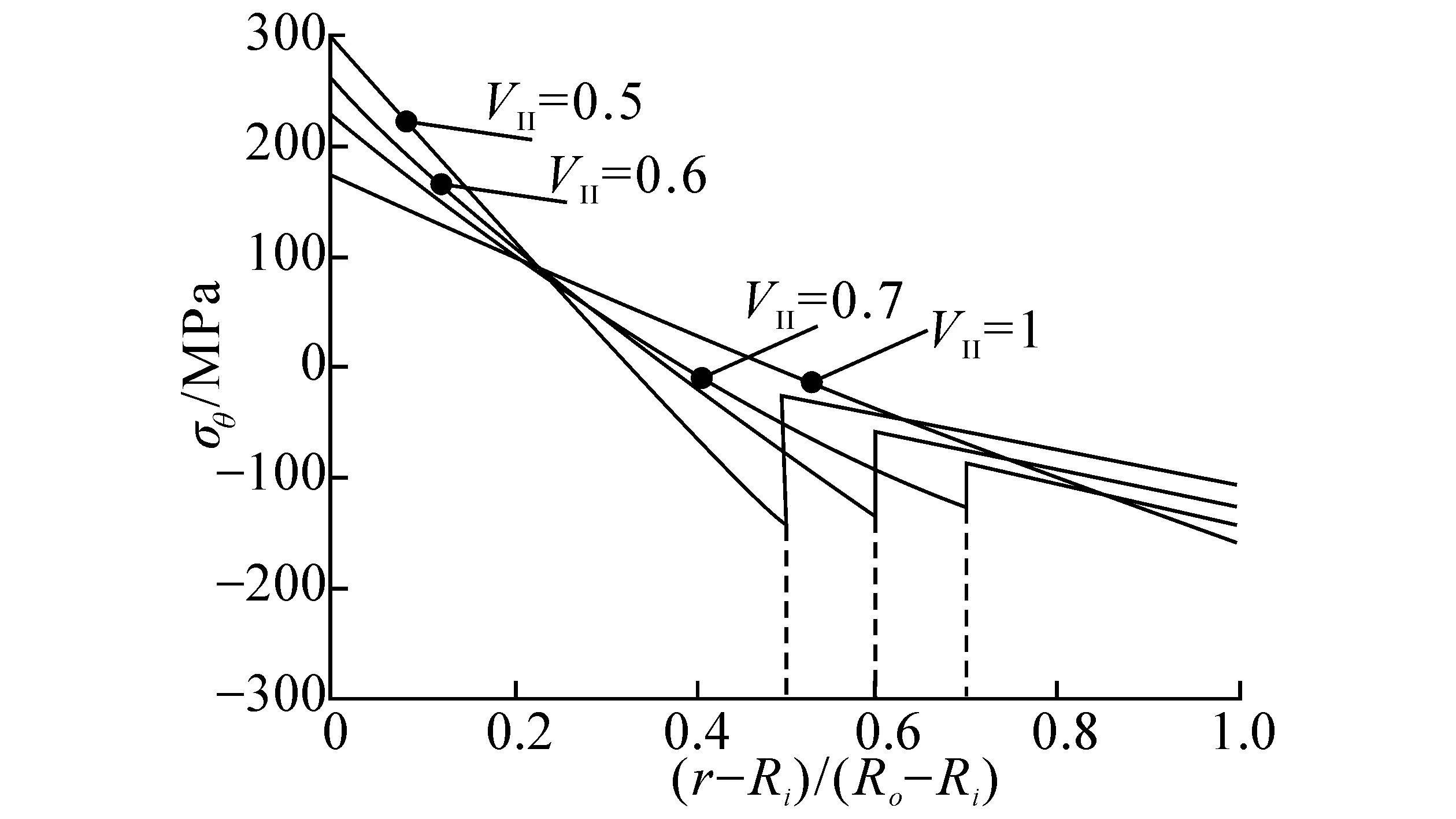
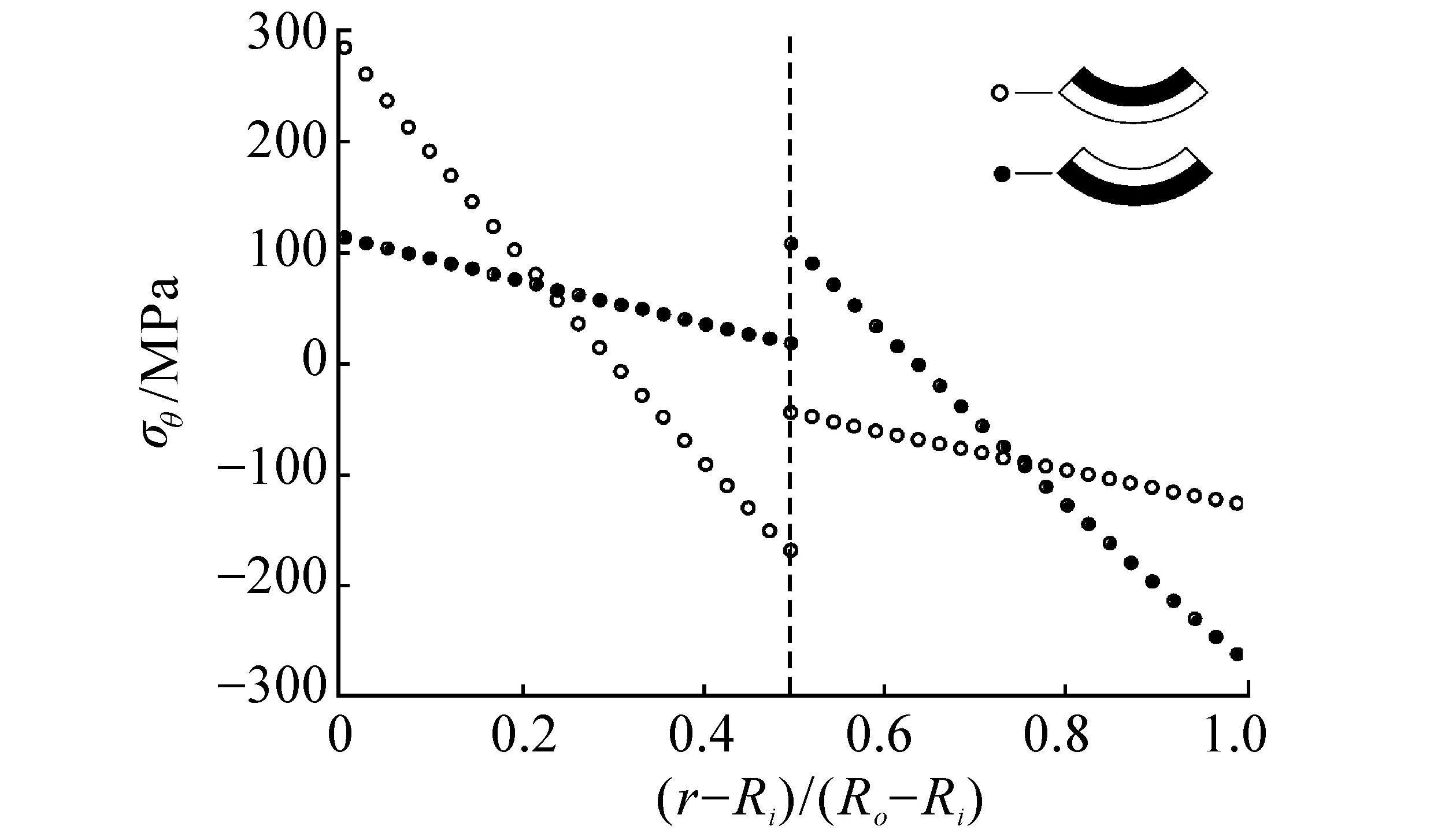
圖5給出了VII為50%、60%、70%下對應(yīng)的應(yīng)力分布。作為比較,圖中還給出了材料II曲梁(VII=100%)的應(yīng)力分布,若Ri=6.4 mm,Ri=9.4 mm,M=1 000 N·m,其中I層II層材料參數(shù)由表1給出。
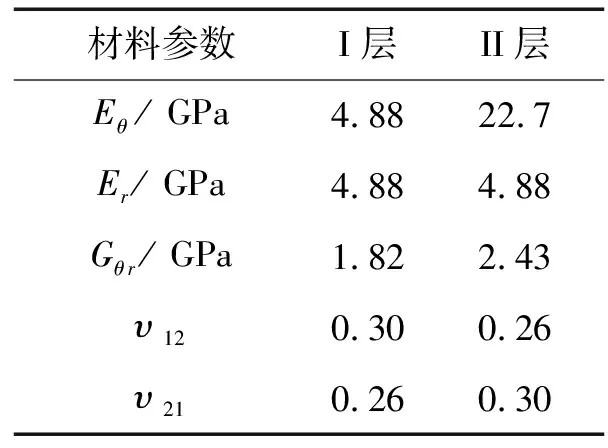
表1 復(fù)合曲梁材料參數(shù)
圖5給出了II層材料體積百分比分別為50%、60%和70%的應(yīng)力分布曲線。其中VII=100%時,最大層間正應(yīng)力約為7.72 MPa,與文獻[15]中7.60 MPa結(jié)果相近。
觀察圖5(a),復(fù)合曲梁層間正應(yīng)力分為2個明顯區(qū)域,分界點橫坐標與材料對應(yīng)的體積百分比一致。從VII=100%到VII=50%,層間正應(yīng)力最大值都位于II層內(nèi),且隨著VII的增加而減小,且層間正應(yīng)力最大值的位置越來越靠近復(fù)合曲梁內(nèi)徑。I層內(nèi)的層間正應(yīng)力最大值位于材料交界處,并沿著外徑方向逐步減至零,隨著VII的增大,I層內(nèi)層間正應(yīng)力最大值增大。
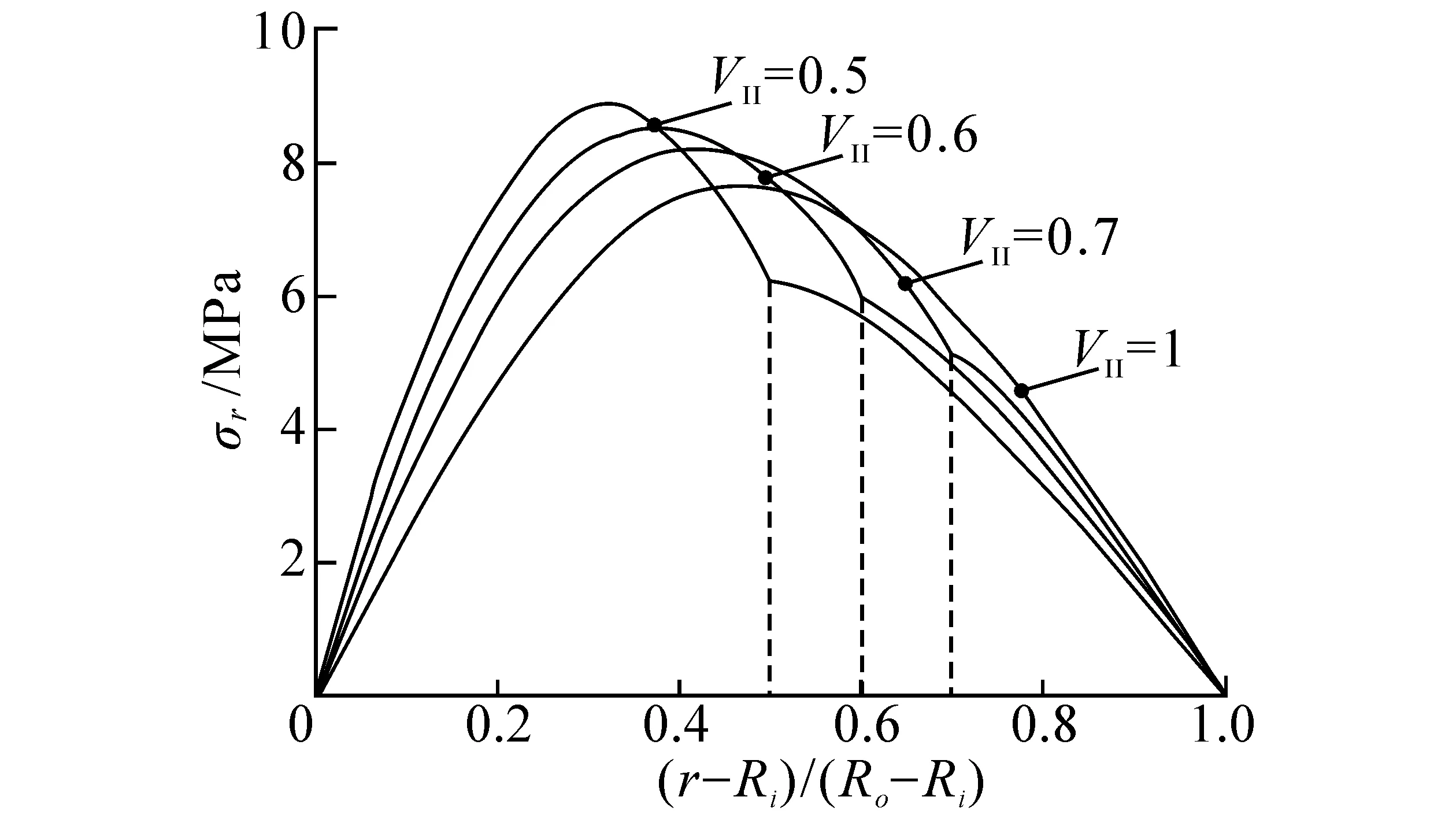
(a) 層間正應(yīng)力分布
(b) 平面內(nèi)正應(yīng)力分布
觀察圖5(b),2種材料不同周向彈性模量,復(fù)合曲梁平面內(nèi)正應(yīng)力存在明顯的分界點,分界點與曲線對應(yīng)的體積百分比一致。隨著VII的減小,II層內(nèi)的平面內(nèi)正應(yīng)力絕對值增大,而I層內(nèi)的平面內(nèi)正應(yīng)力絕對值減小,其中性軸(平面內(nèi)正應(yīng)力為零)也向內(nèi)徑靠近。
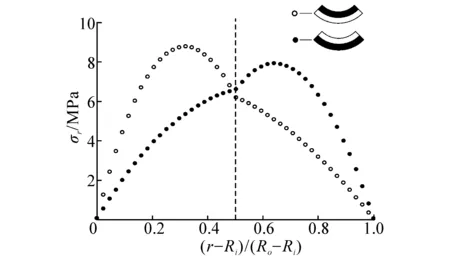
本文將材料I、II位置互換,令材料II位于外徑處,材料I位于內(nèi)徑處。圖6中2種鋪層順序分別用實心點與空心點表示,給出了鋪層順序?qū)?yīng)力分布的影響。
(a) 層間正應(yīng)力分布
(b) 平面內(nèi)正應(yīng)力分布
觀察圖6(a),2種鋪層順序的層間正應(yīng)力的最大值都位于材料II區(qū)域內(nèi),當材料II靠近內(nèi)徑時,層間正應(yīng)力最大值大于材料II靠近外徑時。對于材料I來說,其區(qū)域內(nèi)的層間正應(yīng)力最大值也大于材料I位于外徑處情況。觀察圖6(b),其平面內(nèi)正應(yīng)力分布也呈現(xiàn)同樣的趨勢。
4 結(jié)束語
本文討論了彈性地基作用下曲梁內(nèi)外徑之比(Ri/Ro)與其層間拉應(yīng)力和平面內(nèi)拉應(yīng)力分布的關(guān)系。隨著Ri/Ro的增大,層間拉應(yīng)力最大值減小,最大拉應(yīng)力位置逐步向幾何中心軸靠近,平面內(nèi)拉應(yīng)力值也隨之增大,而平面內(nèi)拉應(yīng)力的中性軸相對位置幾乎不變。
在此基礎(chǔ)上,分析了兩層不同材料組成的曲梁,確定了平面內(nèi)拉應(yīng)力中性軸位置,給出了復(fù)合曲梁的層間拉應(yīng)力和平面內(nèi)拉應(yīng)力解答,計算了不同幾何外形、材料不同的體積分數(shù)和材料參數(shù)對于曲梁層間正應(yīng)力和平面內(nèi)正應(yīng)力大小、鋪層順序的影響。
參考文獻:
[1]TAN E L, UY B. Experimental study on curved composite beams subjected to combined flexure and torsion[J]. Journal of Constructional Steel Research, 2009, 65(8): 1855-1863.
[2]WANG W, SHENOI R A. Delamination modeling of a curved composite beam subjected to an opening bending moment[J]. Journal of Strain Analysis for Engineering Design, 2003, 38(5): 453-457.
[3]PAGANO N J. Exact solution for composite laminates in cylindrical bending[J]. Journal of Composite Materials, 1969, 3(3): 398-411.
[4]PAGANO N J. Analysis of the flexure test of bidirectional composites[J]. Journal of Composite Materials, 1967, 1(4): 336-442.
[5]LEKHNITSKII S G. Bending of a curved rod by moments and a force applied at the ends, theory of elasticity of an anisotropic body[M]. Moscow:Mir. Pub.,1981,
[6]ASTMD6415/D6415M-06a. Standard test method for measuring the curved beam strength of a fiber-reinforced polymer-matrix composite[S]. West Conshohocken: American Society for Testing and Materials, 1999.
[7]SHENOI R A,WANG W. Flexural behavior of a curved orthotropic beam on an elastic foundation[J]. Journal of Strain Analysis for Engineering Design, 2001, 36(1): 1-16.
[8]李永勝,王瑋波,張效慈.考慮彈性地基的復(fù)合材料曲梁徑向應(yīng)力的研究[J].船舶力學, 2009, 13(4): 593-602.
LI Yongsheng, WANG Weibo, ZHANG Xiaoci. A study of through-thickness stresses in curved layered composite beams on a elastic foundation[J]. Journal of Ship Mechanics, 2009, 13(4): 593-602.
[9]LO K H, CHRISTENSEN R M, WU E M. Stress solution determination for high order plate theory[J]. International Journal of Solids Structure,1978, 14(8): 655-662.
[10]REDDY J R. A simple higher order theory for laminated composite plates[J]. Journal of Applied Mechanics, 1984, 51(12):745-752.
[11]SHENOI R A, WELLICOME J F. Composite materials in maritime structures, ocean technology series[M]. London:Cambridge University Press,1993.
[12]TOLF G. Stress in a curved laminated beam[J]. Fiber Science and Technology,1983,19:243-67.
[13]LU T J, XIA Z C,HUTCHINSON J W. Delamination of beams under transverse shear and bending[J]. Materials Science and Engineering, 1994, A188: 103-112.
[14]SHENOI R A, WANG W. Analytical solutions to predict flexural behavior of curved sandwich beams[J]. Sandwich Structures and Materials, 2004, 6: 199-216.
[15]SHENOI R A, WANG W. Through-thickness stresses in curved composites laminates and sandwich beams[J]. Composites Science and Technology,2001,61:1501-1512.

