具有輸入與狀態(tài)時(shí)變時(shí)滯線性系統(tǒng)的魯棒H∞控制
侯曉麗 ,邵誠(chéng),李永鳳
(1.鄭州輕工業(yè)學(xué)院 數(shù)學(xué)與信息科學(xué)系,河南 鄭州 450002;2.大連理工大學(xué) 電信學(xué)院,遼寧 大連 116085)
時(shí)滯現(xiàn)象存在于許多實(shí)際系統(tǒng),如生物系統(tǒng)、經(jīng)濟(jì)系統(tǒng)、化工系統(tǒng)、物理系統(tǒng),電力系統(tǒng)等,時(shí)滯的存在有時(shí)會(huì)導(dǎo)致系統(tǒng)不穩(wěn)定,或使得系統(tǒng)的性能下降。近年來,對(duì)具有輸入時(shí)滯和狀態(tài)時(shí)滯的線性系統(tǒng)的魯棒控制及H∞控制已有大量的研究成果[1-10],其中很多文獻(xiàn)要求系統(tǒng)是能控的且時(shí)滯依賴的結(jié)果大都要求時(shí)滯的導(dǎo)數(shù)小于1,但在很多實(shí)際系統(tǒng)中,可能無法預(yù)知時(shí)滯參數(shù)導(dǎo)數(shù)的情況, 如遙操作系統(tǒng)和網(wǎng)絡(luò)控制系統(tǒng)中的時(shí)滯參數(shù)變化很快, 有時(shí)時(shí)滯參數(shù)的導(dǎo)數(shù)甚至可能不存在, 這時(shí)已有方法就不適用了。有的結(jié)果對(duì)時(shí)滯導(dǎo)數(shù)沒有限制,如鄭敏等[11]對(duì)一類狀態(tài)及輸入具有區(qū)間變時(shí)滯的線性系統(tǒng),基于時(shí)滯劃分形式的泛函,討論系統(tǒng)的鎮(zhèn)定問題;王新梅等[12]利用一個(gè)積分等式,給出了一類區(qū)間時(shí)變輸入時(shí)滯與狀態(tài)時(shí)滯線性系統(tǒng)的時(shí)滯相關(guān)穩(wěn)定性判據(jù)等,但結(jié)果有一定的保守性。
對(duì)沒有不確定性和外擾的系統(tǒng),結(jié)合自由權(quán)矩陣技巧,不經(jīng)過任何不等式放縮,利用Lyapunov穩(wěn)定性定理,得到了系統(tǒng)漸近穩(wěn)定的時(shí)滯依賴充分性條件,且對(duì)時(shí)滯的導(dǎo)數(shù)沒有任何限制,解決了穩(wěn)定性問題中保守性產(chǎn)生的根源。然后把該方法用于不確定系統(tǒng),研究其魯棒控制與H∞控制。
1 系統(tǒng)描述及主要結(jié)果
考慮具有如下形式的不確定時(shí)滯系統(tǒng):
(1)
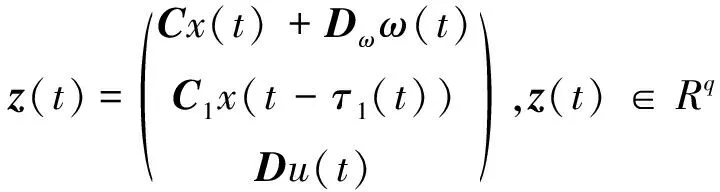
假設(shè)參數(shù)不確定性為范數(shù)有界的,即存在適當(dāng)維數(shù)的常值矩陣E、G1、G2、G3、G4,使得
式中:F(t)∈Ri×j為未知的時(shí)變函數(shù)矩陣,其元素為可測(cè)的且滿足FT(t)F(t)≤I?t。
引理[10]假定存在適當(dāng)維數(shù)的相容矩陣M、N和正定對(duì)稱矩陣R、Q,對(duì)任意滿足FTF≤R的F有Q+MFN+NTFTMT<0成立等價(jià)于存在標(biāo)量λ>0使得Q+λMMT+λ-1NTRN<0成立。
目的是設(shè)計(jì)狀態(tài)反饋控制器u(t)=Kx(t),使得從外部擾動(dòng)輸入ω(t)到被調(diào)輸出z(t)的傳遞函數(shù)Tωz小于給定的正數(shù)γ。
先考慮沒有不確定性的系統(tǒng):
(2)
定理1 對(duì)系統(tǒng)(2),在狀態(tài)反饋u(t)=Kx(t)作用下,若存在正定對(duì)稱矩陣P,Qi(i=1、2、3、4),適當(dāng)維數(shù)的相容矩陣Ni(i=1、2、3、4)和Mi(i=1、2、3),使得下述不等式成立,則其是漸近穩(wěn)定的:
(9)
其中,
證明:把狀態(tài)反饋u(t)=Kx(t)代入系統(tǒng)(2)可得
取泛函:
則對(duì)V沿系統(tǒng)(2)對(duì)t求導(dǎo),得
ri)Qix(t-ri)=2xTP(A0+B1K)x(t)+
2xTPA1x(t-τ1(t))+2xTPB2Kx(t-τ2(t))+
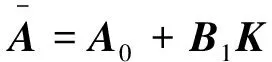
令
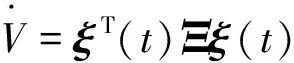
由Lyapunov穩(wěn)定性定理知,系統(tǒng)是漸近穩(wěn)定的。證畢。
整個(gè)證明過程可以看到?jīng)]有任何不等式放縮,所以結(jié)果沒有任何保守性。對(duì)時(shí)滯的導(dǎo)數(shù)沒有任何限制,適合快變與慢變系統(tǒng),且結(jié)果是時(shí)滯依賴的,與時(shí)變時(shí)滯的上下界有關(guān)。
對(duì)添加等式中的項(xiàng)數(shù)可根據(jù)需要而定。比如若系統(tǒng)中沒有時(shí)滯項(xiàng),則添加等式的方括號(hào)中可只選第一項(xiàng)和最后一項(xiàng),其他項(xiàng)可以不要。
對(duì)含有不確定性的系統(tǒng)
(3)
同理可得下面的定理。
定理2 對(duì)系統(tǒng)(3),在狀態(tài)反饋u(t)=Kx(t)作用下,若存在正定對(duì)稱矩陣P,Qi(i=1,2,3,4),適當(dāng)維數(shù)的相容矩陣N0和Mi(i=1,2,3),以及正數(shù)εi、ai、bi、ci、di(i=1,2,3,4),使得下述不等式成立,則系統(tǒng)(3)是漸近穩(wěn)定的:

其中,
證明:與定理1的證明類似,添加等式:
令
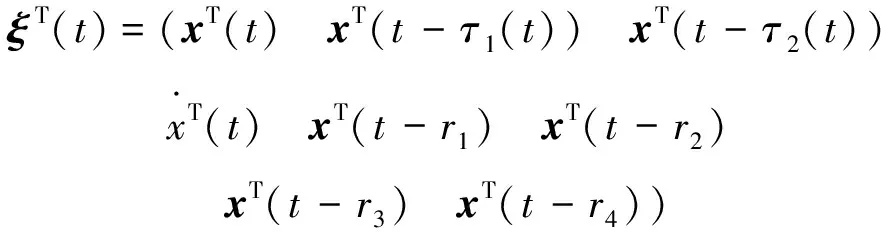
由引理1,結(jié)論即可得證。
下面考慮不確定時(shí)滯系統(tǒng)的H∞控制:
定理3 對(duì)系統(tǒng)(1),在狀態(tài)反饋u(t)=Kx(t)作用下,若存在正定對(duì)稱矩陣P,Qi(i=1,2,3,4),適當(dāng)維數(shù)的相容矩陣N0和Mi(i=1,2,3),以及正數(shù)εi,ai,bi,ci,di(i=1,2,3,4),使得下述不等式成立:
T=
則系統(tǒng)(1)漸近穩(wěn)定,且從外部擾動(dòng)輸入ω(t)到被調(diào)輸出z(t)的傳遞函數(shù)Tωz小于給定的正數(shù)γ。其中,
2 數(shù)值算例
例1 考慮如下系統(tǒng):
其中,
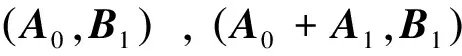
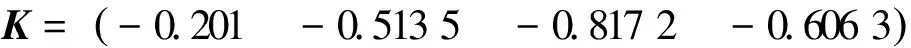
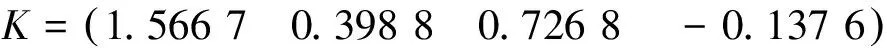
可見定理1的方法所得結(jié)果更好。
例2 考慮線性不確定時(shí)滯系統(tǒng):
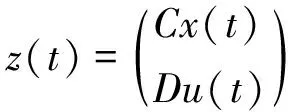
其中,
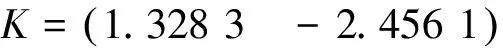

表1 性能指標(biāo)與控制增益與其他文獻(xiàn)對(duì)比結(jié)果
3 結(jié)束語(yǔ)
利用自由權(quán)矩陣技巧,研究了具有時(shí)變輸入時(shí)滯與狀態(tài)時(shí)滯的不確定系統(tǒng)的魯棒H∞控制,所得結(jié)果是時(shí)滯依賴的,與時(shí)變時(shí)滯的上下界有關(guān)。從定理1的證明可以看出,沒有任何不等式的放縮,所以定理1的結(jié)果沒有任何保守性,且所設(shè)計(jì)的Lyapunov泛函簡(jiǎn)單,對(duì)時(shí)滯的導(dǎo)數(shù)也沒有限制。
參考文獻(xiàn):
[1]CHOI H H, CHUNG M J. Memory less stabilization of uncertain dynamic systems with time varying delayed state and control[J]. Automatic, 1995, 31(9): 1349-1351.
[2]KIM J H, JEUNG E T, PARK H B. Robust control for parameter uncertain delay systems in state and control input[J]. Automatic, 1996, 32(9): 1337-1339.
[3]HAN Q L, MEHDI D. Comments on robust control for parameter uncertain delay systems in state and control input[J]. Automatic, 1998, 32(12) : 1665-1666.
[4]LEE Y S, MOON Y S, KWON W H. Delay dependent robust H∞control for uncertain systems with a state delay[J]. Automatic, 2004, 40:65-72.
[5]FRIDMAN U A.Descriptor system approach to H∞control of linear time delay system[J].IEEE Transactions on Automatic control,2002, 47: 253-270.
[6]李永釗,吳保衛(wèi).帶狀態(tài)時(shí)滯和輸入時(shí)滯的非線性系統(tǒng)的魯棒H∞控制[J].河南師范大學(xué)學(xué)報(bào),2010,38(2):2-7.
LI Yongzhao, WU Baowei. Robust H∞control for nonlinear system with input time delay and state delay[J].Journal of Henan Normal University,2010,38(2):2-7.
[7]ZHOU Shaosheng, WEI Xingzheng. Robust H∞control of delayed singular systems with linear fractional parametric uncertainties[J].Journal of the Franklin Institute, 2009, 346: 147-158.
[8]FANG Wei. Delay dependent robust H∞control f or uncertain singular systems with state delay[J].Act Automatic Sinica, 2009, 35: 65-70.
[9]ZHANG Xianming, HAN Qinglong. Robust H∞filtering for a class of uncertain linear systems with time varying delay[J]. Automatica,2008, 44: 157-166.
[10]FRIDAM E, SHAKED U. Delay dependent stability and H∞control: Constant and time varying delays[J].Int J of Control, 2003, 76(9) : 48-60.
[11]鄭敏,費(fèi)樹岷.一類狀態(tài)及輸入均有區(qū)間變時(shí)滯的線性系統(tǒng)之鎮(zhèn)定[J].控制理論與應(yīng)用,2008,25(5):956-958.
ZHENG Min, FEI Shumin. Stabilization for linear system with input time delay and state delay[J].Control Theory and Application, 2008,25(5):956-958.
[12]王新梅,裴海龍.一類區(qū)間時(shí)變輸入時(shí)滯與狀態(tài)時(shí)滯線性系統(tǒng)的穩(wěn)定性研究[J].控制與決策,2009,24(10):1549-1554.
WANG Xinmei,PEI Hailong. Stability research for linear system with input time delay and state delay[J]. Control and Decision, 2009,24(10):1549-1554.

