彈性支承對三維曲壁板顫振特性的影響

張飛霆，楊智春，高 揚，趙令誠

（西北工業大學 航空學院結構動力學與控制研究所，西安 710072）

自20世紀50年代飛行器速度達到超音速以來，壁板顫振問題已受到普遍關注，許多學者對其進行了理論和試驗研究。壁板顫振是飛行器表面蒙皮結構由于空氣動力、慣性力和彈性力的相互耦合作用而產生的一種氣動彈性不穩定現象，是一種自激振動。壁板顫振雖然不會導致飛行器結構迅速的發生破壞，但其所引發的結構疲勞裂紋問題會嚴重影響飛行器壽命和飛行安全。為了避免這種有害的振動，對壁板結構進行合理的設計就顯得尤為重要。Plaut［1］就針對鋁合金壁板，在壁板不發生顫振的約束條件下，對壁板的厚度分布進行了優化設計，以達到減輕重量的目的。Pier-son［2］針對帶有氣動阻尼的壁板優化問題進行了數值分析，研究指出氣動阻尼在一定的范圍之內時，氣動阻尼的增大，有助于減輕壁板的重量。Dowell［3］從定量和定性方面詳細的討論了曲壁板非線性顫振特性，指出壁板沿順氣流方向的曲率會減小顫振臨界動壓、增加非線性顫振幅值，由于板的初始曲率引入的氣動靜載荷將對曲壁板的顫振邊界產生較大的影響，在處理曲壁板顫振問題時應考慮靜態載荷產生的靜變形。Azzouz等［4－6］應用有限元方法系統研究了初始拱高、熱載荷和氣流偏角等因素對曲壁板顫振特性的影響，研究表明隨著初始拱高的增大，顫振是由更高階模態耦合產生的；隨著溫度的升高，顫振臨界動壓逐漸下降。在國內，張蕊麗等［7］在曲壁板的非線性顫振方面做了初步的研究，指出初始幾何曲率和溫升的變化會改變曲壁板顫振失穩的耦合模態。楊智春等［8］對超音速氣流中二維受熱曲壁板顫振行為進行了研究，分析了動壓參數對二維曲壁板分叉特性的影響，指出初始幾何曲率和氣動熱效應使得曲壁板的動力學特性更為復雜。這些工作都是針對曲壁板顫振特性分析而開展的，沒有涉及到提高曲壁板顫振動壓的研究。

隨著新一代飛行器設計馬赫數的提高，高超音速飛行器蒙皮壁板防顫振設計的首要任務是提高曲壁板顫振速度，而工程中常用的提高壁板顫振速度方法，就是增加壁板厚度或對壁板加筋，但是這種措施會帶來壁板結構重量增加的負面效應，尋求其他提高曲壁板顫振速度的方法，是一項既有學術意義又有工程應用背景的研究工作。本文提出了一種在曲壁板上附加一個彈性支承來提高其顫振動壓的方法，應用頻率重合理論探究了彈性支承位置以及支承剛度對曲壁板顫振動壓的影響規律，并對采用附加彈性支承的防壁板顫振設計提出了相應建議。

1 曲壁板的顫振運動方程

考慮如圖1所示超聲速氣流中帶一個附加彈性支承的圓柱殼金屬曲壁板，氣流沿x軸方向。圖2為曲壁板上任一點的變形。

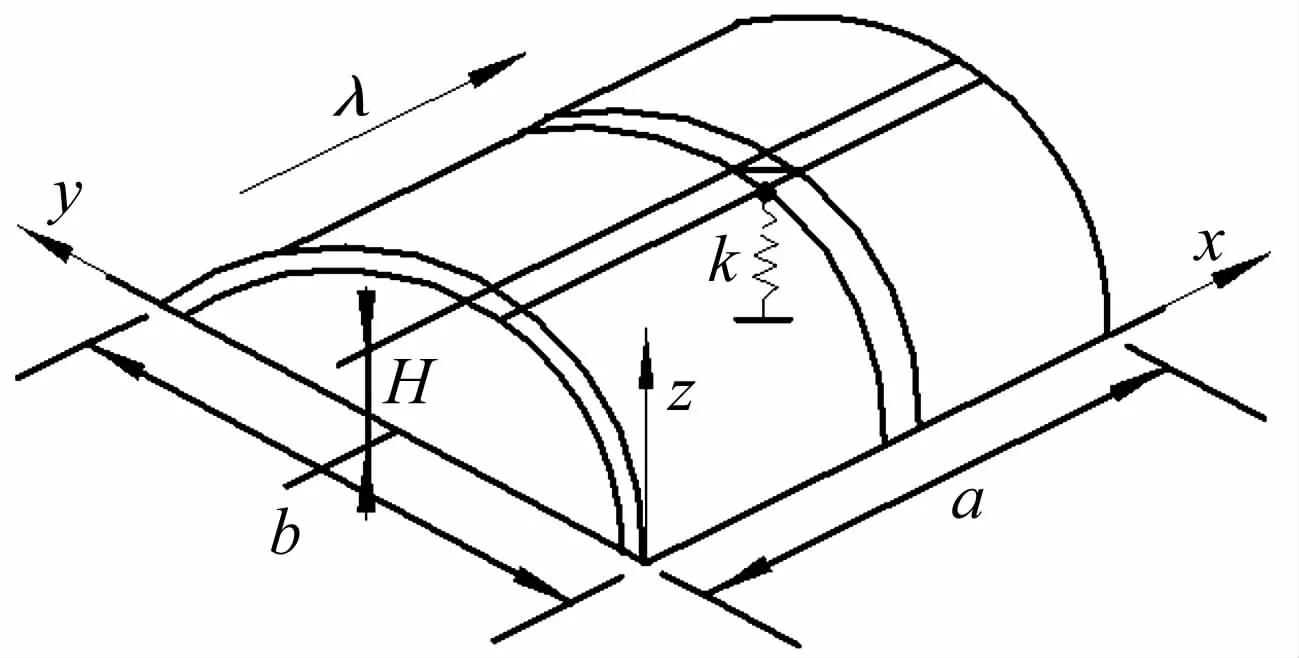
圖1 附加彈性支承的金屬曲壁板模型Fig．1 The physicalmodal ofmetalmaterial curved panelwith concentrated elastic support

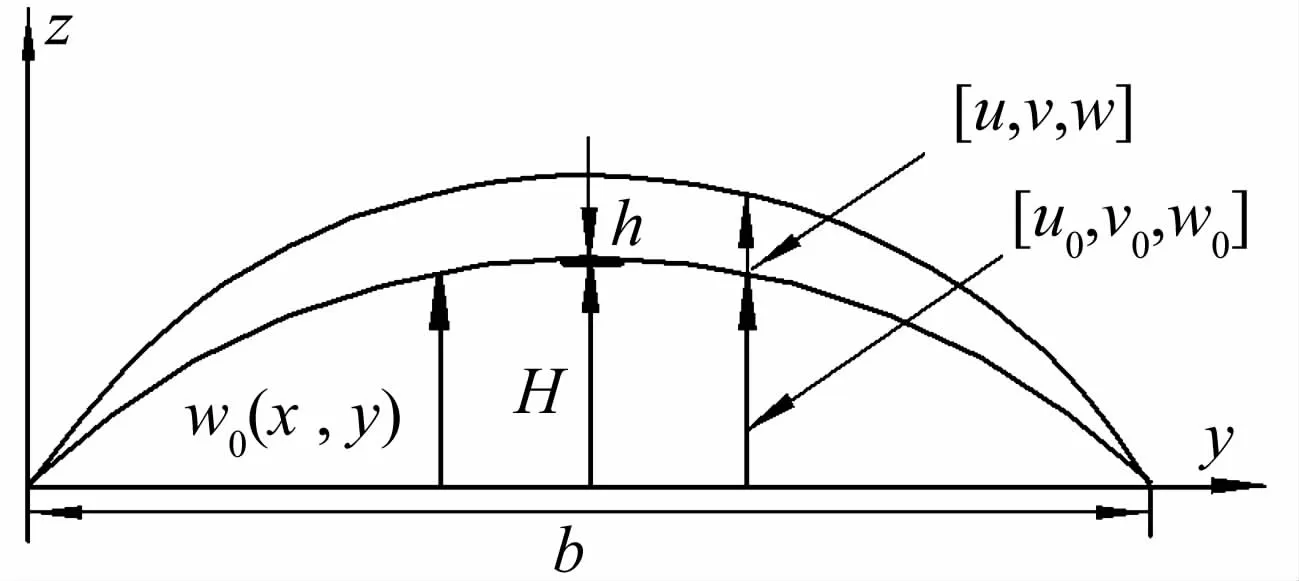
圖2 曲壁板上任一點的變形Fig．2 Coordinates details of a point belonging to the curved panel

當考慮附加彈性支承時，通常采用兩個簡化假設：

（1）只考慮彈性支承在z軸方向的線性剛度，即認為支承是線性點支承；

（2）支承是理想無質量的彈性元件。因此，只需考慮彈性支承對曲壁板總體剛度矩陣的影響。

壁板的位移矢量包括兩個面內位移u和v，兩個分別繞x和y軸的法線轉角位移，彎曲位移w。根據von Karman大變形應變－位移關系，曲壁板的總應變為中面位移產生的應變、考慮大變形時撓度引起的面內附加應變、彎曲產生的應變和曲壁板初始拱高w0＝w0（x，y）引起的Marguerre應變的和。

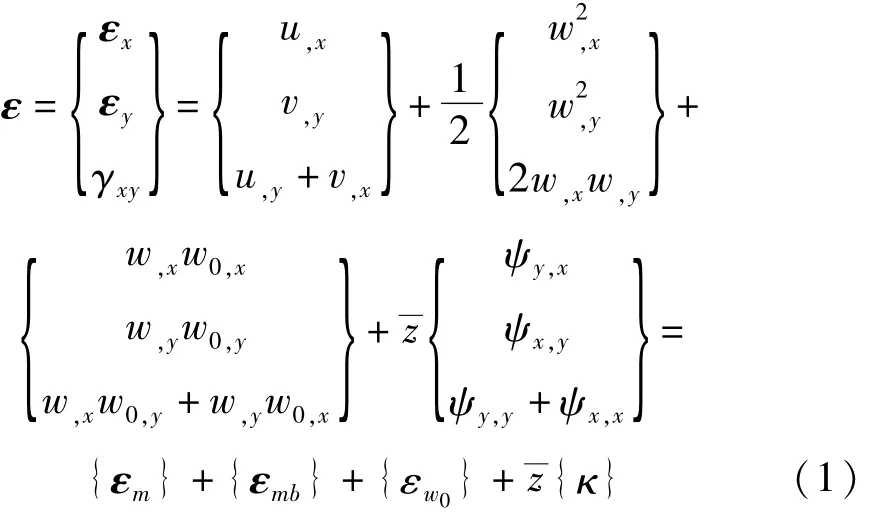
橫向剪切應變為

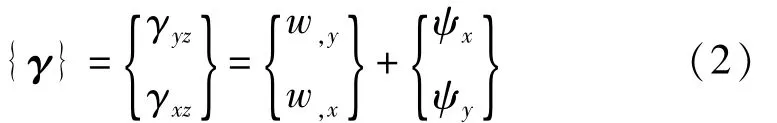
曲壁板表面的氣動力采用一階活塞氣動力理論計算，其表達式為：

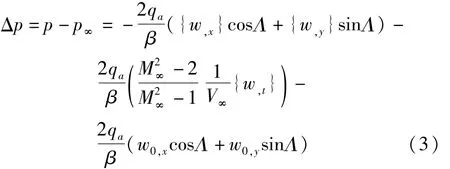
qa＝為氣流的動壓為 Prandtl－Glauert因子，V∞為氣流速度，M∞為氣流馬赫數，Λ為氣流與x軸的夾角。w，t為彎曲位移對時間t的一階導數。w0，x，w0，y分別是曲板初始幾何形狀 w0（x，y）對坐標x和y的導數。式（3）的前兩項與平壁板的活塞氣動力表達式相同，最后一項為順氣流方向上曲壁板初始曲率引起的氣動靜載荷。

對于處于平衡狀態的結構，根據虛功原理，內力虛功等于外力虛功

曲壁板的單元內力虛功的表達式為

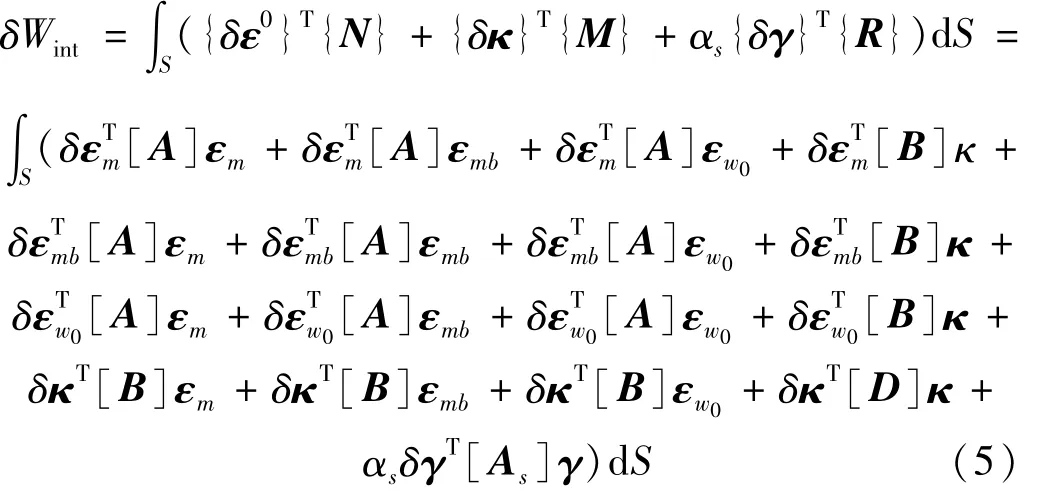
S為壁板單元面積，αs為橫向剪切修正因子。

單元外力虛功的表達式為

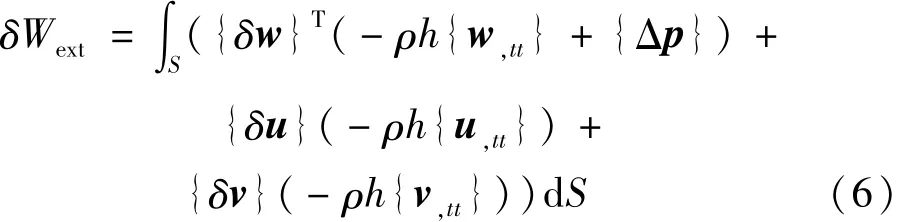
當沒有彈性支承時，經過單元組裝，得到整個曲壁板結構的內力虛功及外力虛功分別為［5］

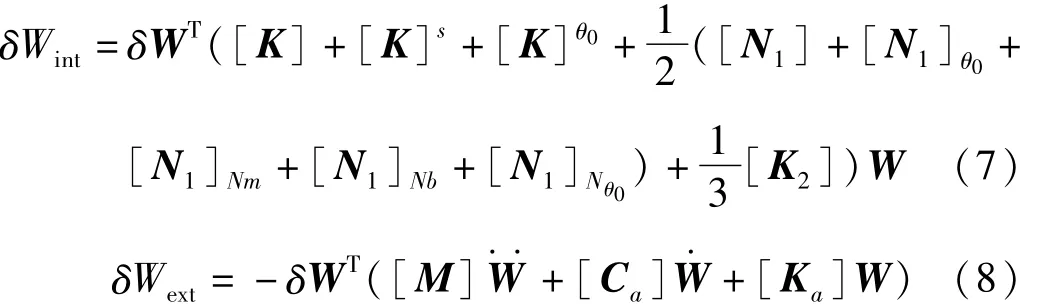
式中，［M］為曲壁板的結構質量矩陣，［Ca］為氣動阻尼矩陣，［Ka］為氣動剛度矩陣，［K］為線性剛度矩陣，［K］s為剪切剛度矩陣，［K］θ0為由初始幾何曲率影響矩陣引起的線性剛度矩陣，［N1］為考慮von Karman非線性應變位移關系后，與結點位移一次項有關的一階非線性剛度矩陣，［N1］θ0為由初始幾何曲率影響矩陣引起的一階非線性剛度矩陣，［N1］Nm為由面內變形｛wm｝引起的一階非線性剛度矩陣，［N1］Nb為由面外彎曲變形｛wb｝引起的一階非線性剛度矩陣，［N1］Nθ0為由初始幾何曲率影響矩陣、面外彎曲變形｛wb｝和扭轉變形｛wψ｝引起的一階非線性剛度矩陣，［K2］為與結點位移二次項有關的二階非線性剛度矩陣，｛W｝為位移向量。

因為一階非線性剛度矩陣和二階非線性剛度矩陣都是經過組裝形成的總體剛度矩陣，階數相同，因此在計算時可以相加。

當在曲壁板上附加一個彈性支承時，曲壁板結構的內力虛功表示為

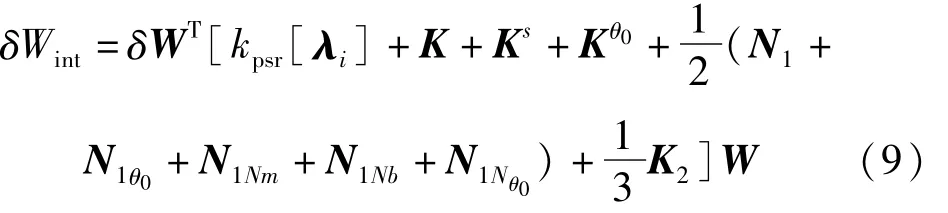
kspr為彈性支承的剛度系數，［λi］為支承彈簧的定位矩陣，下角標i表示集中彈性支承的附加結點位置編號，結點編號由有限元網格劃分決定，當附加彈性支承位于結點i時，該矩陣對應的第（i，i）元素置1，其他的元素均置0。

由虛功原理，可得到帶有一個彈性支承的曲壁板非線性顫振運動方程為

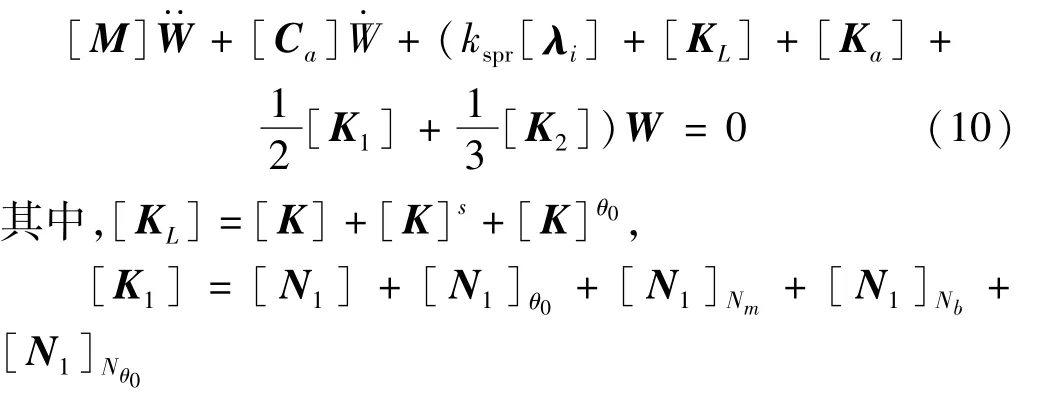
由于本文研究中，氣流方向沿圓柱殼母線方向，氣流作用下曲壁板無靜變形，則非線性顫振運動方程（10）中的一階非線性剛度矩陣和二階非線性剛度矩陣均為零矩陣。從而方程（10）退化為曲壁板的線性顫振運動方程

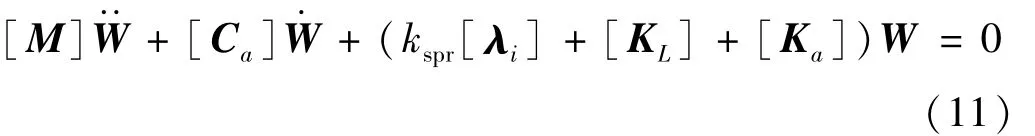
2 曲壁板的顫振運動方程求解

曲壁板的線性顫振運動方程（11）可采用特征值法求解。引入無量綱化的動壓λ：

D110表示曲壁板彎曲剛度矩陣［D］的第一個對角線項D（1，1），a為壁板順氣流方向的長度。

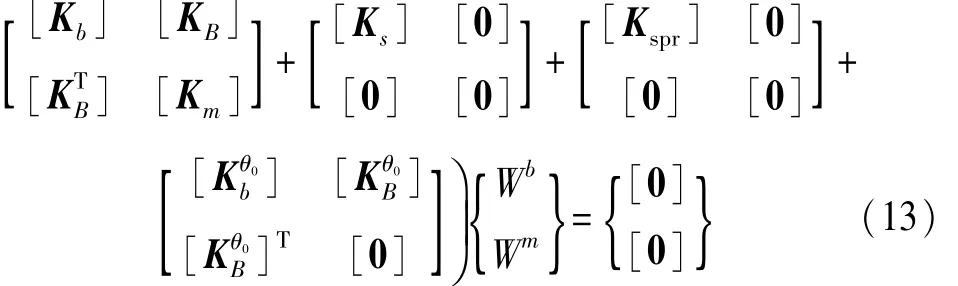
上標θ0表示該矩陣與曲壁板的初始幾何曲率影響矩陣有關。展開式（13）的第二行可以得到

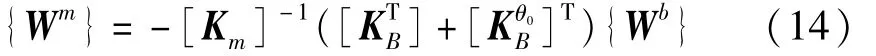
展開式（13）的第一行并將式（14）帶入，可得只包含曲壁板離面位移的氣動彈性顫振運動方程：

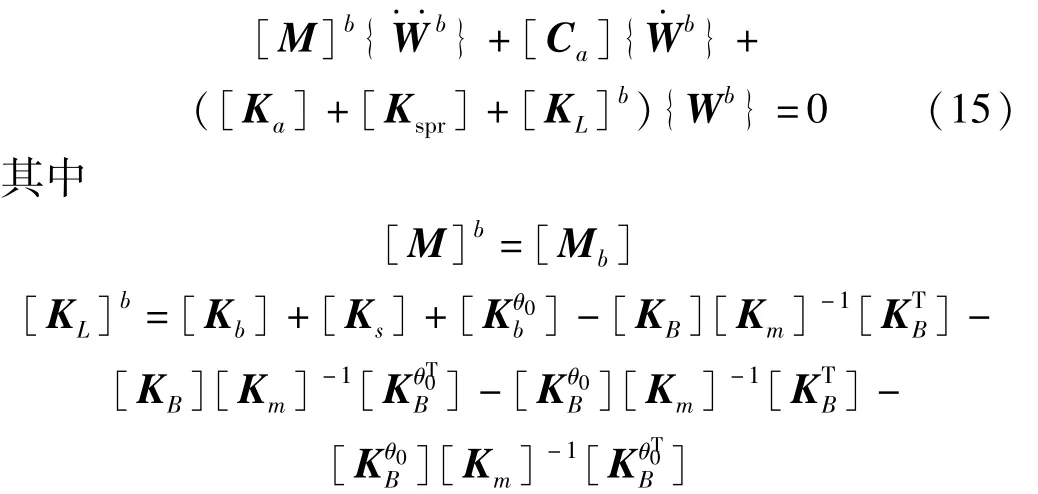
假設曲壁板在顫振臨界點的響應為

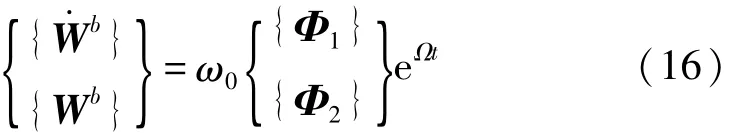
將式（16）代入氣動彈性顫振運動方程中得

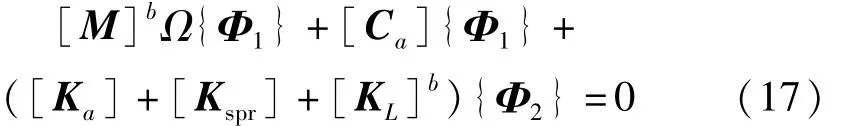
化為矩陣形式，則附加彈性支承的系統特征方程

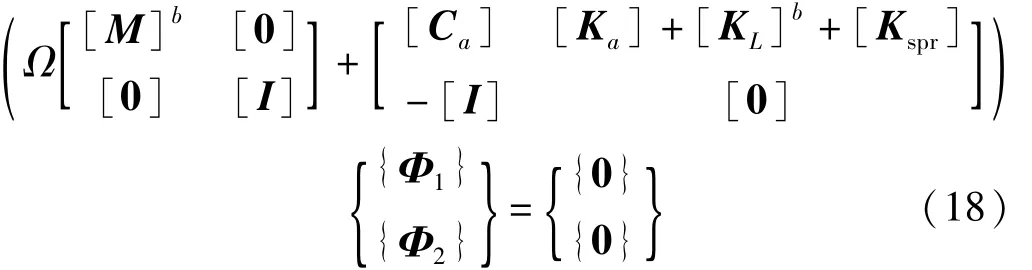
由式（18）的系統特征方程計算在不同λ下壁板顫振系統的特征值Ω＝ΩR＋iΩI，從復特征值實部的正負號即可判斷曲壁板顫振系統的穩定性。繪制出λ～ΩR曲線，插值得到ΩR＝0所對應的λ，即為曲壁板顫振臨界動壓 λcr。

3 數值算例分析與討論

采用文獻［9］中的超音速飛行器鋁合金曲壁板作為研究對象，其力學性能參數見表1。

表1 鋁合金的力學性能參數Tab．1 Themechanical properties of alum inum alloy

曲壁板四邊簡支，投影平面為矩形，幾何尺寸為：0．38 m×0．305 m，厚度為 h＝0．002 m，最大初始拱高為H＝0．002 m，曲壁板有限元模型如圖3所示。

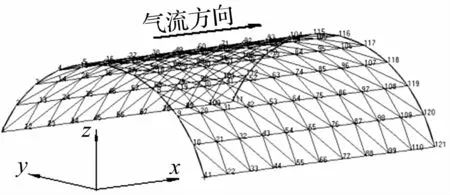
圖3 曲壁板有限元模型Fig．3 Curved panel Finite elementmodal

曲壁板有限元模型的結點編號如俯視投影圖4所示。為了更簡潔的表示彈性支承在壁板上的位置，下文的結果討論中，采用了歸一化的坐標 ξ＝x／a，η＝y／b。考察彈性支承位置對顫振動壓影響時，彈性支承位置分別沿圖4中A1－A1、B1－B1等網格線在結點上移動。

3.1 彈性支承位置對曲壁板顫振動壓的影響

圖5給出了彈性支承剛度系數為1 000 D（D表示曲壁板的彎曲剛度）時，彈性支承位置改變對曲壁板顫振動壓的影響。從圖中可以看出，當支承位于壁板的中心位置時顫振動壓最小，支承在（ξ，η）＝（0．2，0．5）和（ξ，η）＝（0．8，0．5）處時顫振動壓最大。

圖6繪示了在順氣流方向，曲壁板的顫振動壓隨彈性支承位置變化的趨勢。隨支承位置的移動，曲壁板顫振動壓先增大，當彈性支承位于壁板展向中線距前緣20%弦長處時，曲壁板的顫振動壓達到極大值。然后隨著位置向中點接近顫振動壓開始減小，在中點處（即曲壁板中點位置）達到極小值，隨后顫振動壓又開始增大，在距后緣20%弦長處達到極大值，之后再開始減小。在附加彈性支承前后，曲壁板發生顫振的耦合模態都為其前兩階固有模態，因此產生這種現象的機理，可依據顫振的頻率重合理論進行分析，通過彈性支承位于不同位置時參與曲壁板顫振耦合的各階模態頻率的變化來進行解釋。圖7中可以看到，當支承位于曲壁板中心結點（61點）時，由于彈性支承的作用，曲壁板的前兩階模態頻率分別為178．7 Hz和242．1 Hz，而無附加彈性支承時，曲壁板的前兩階模態頻率分別為165．7 Hz和242．1 Hz。可以看出彈性支承僅使得曲壁板的第1階模態頻率提高而第2階模態頻率保持不變，即第1階模態頻率更加靠近第2階模態頻率，故前兩階模態更容易發生耦合而使得顫振動壓降低。當支承位于結點28時，由于彈性支承作用，曲壁板的前兩階模態頻率分別為169．8 Hz和250．6 Hz，與無彈性支承情況相比，曲壁板的前兩階模態頻率都有所提高，有彈性支承時該兩階模態的頻率之差為80．8 Hz，而無彈性支承時該兩階頻率之差為76．4 Hz，即彈性支承使得曲壁板前兩階頻率之差變大，根據顫振的頻率重合理論，其顫振動壓得到提高。

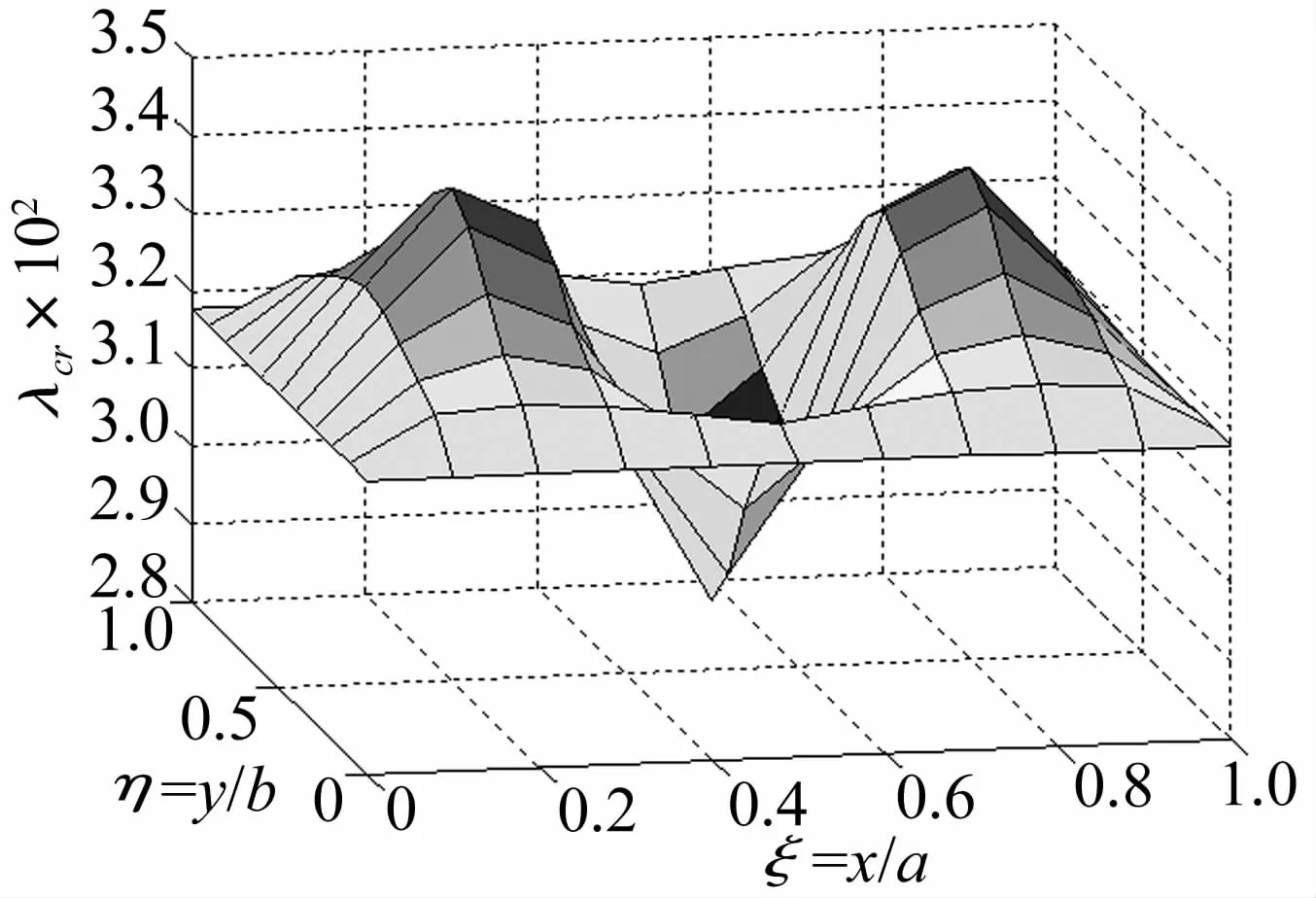
圖5 集中彈性支承位置對顫振動壓的影響Fig．5 The influence of concentrated elastic support to dynamic pressure

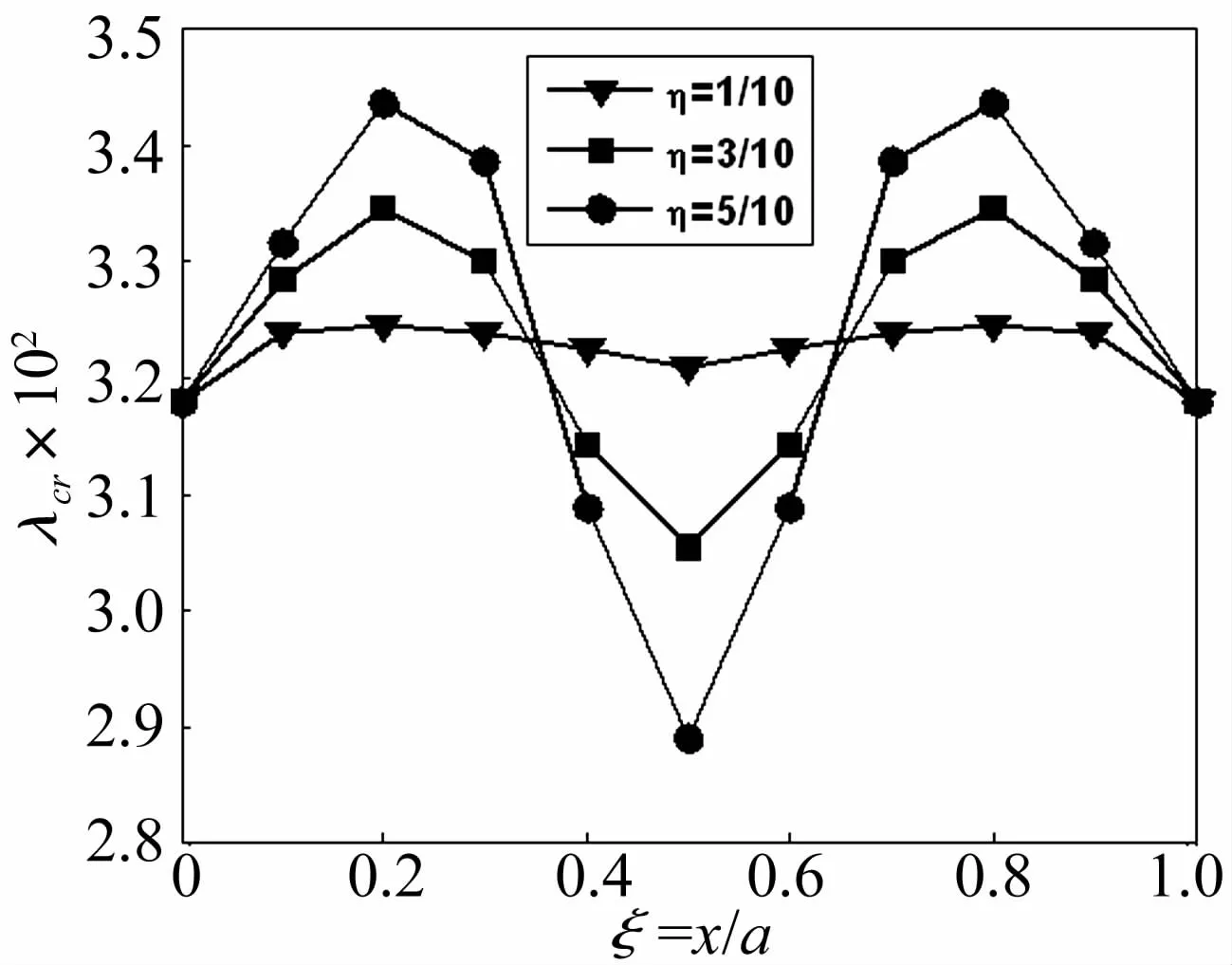
圖6 順氣流方向顫振動壓隨支承位置的變化Fig．6 Dynamic pressure vs elastic support position

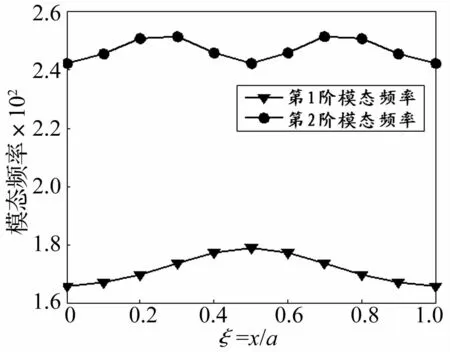
圖7 模態頻率隨支承位置的變化（支承在A1－A1截線）Fig．7 Modal frequency vs elastic support position

圖8繪示了彈性支承位置在垂直氣流方向移動時，曲壁板顫振動壓的變化趨勢。圖9繪示了彈性支承位于曲壁板中線（ξ＝5／10）上不同結點位置時，前兩階模態頻率的變化曲線。

從圖8看到，當彈性支承靠近曲壁板邊界（ξ＝1／10和 ξ＝3／10）時，對其顫振動壓影響較小，隨著支承位置向曲壁板中線移動，顫振動壓也隨之增大，而當彈性支承在與上述網格線幾何位置對稱的兩條網格線（ξ＝7／10和 ξ＝9／10）上移動時，顫振動壓隨支承位置變化的曲線分別與其相應對稱網格線的動壓曲線基本重合，說明在順氣流方向，彈性支承位置在前后緣處顫振動壓幾乎沒有差別。如圖9（a）所示，這是由于當彈性支承位于靠近簡支邊界位置（例如B2－B2網格線）時，使得曲壁板前兩階模態頻率都發生變化，但前兩階模態頻率之差都大于不帶彈性支承的情況，使得帶彈性支承后曲壁板顫振動壓得到提高。

圖8中ξ＝5／10的曲線可以看出，當彈性支承位于曲壁板結構垂直氣流方向的中線位置時，隨著支承向曲壁板中心點位置移動，顫振動壓達到一個極小值，然后又逐漸增大。

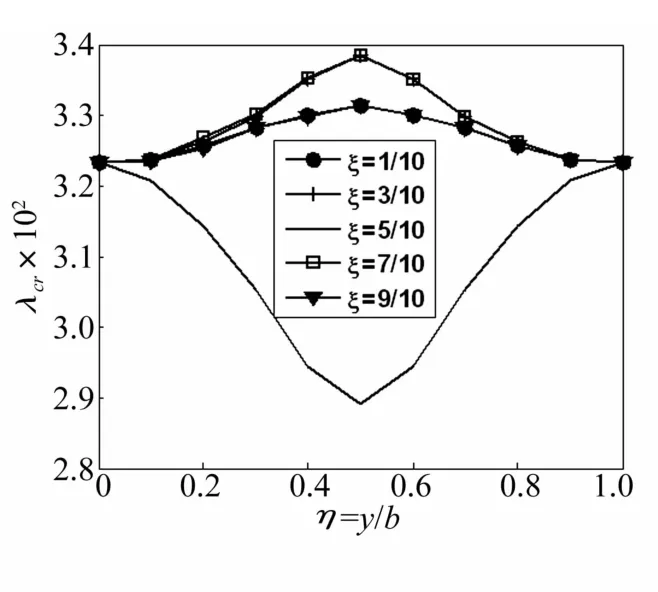
圖8 垂直氣流方向顫振動壓隨支承位置的變化Fig．8 Dynamic pressure vs elastic support position

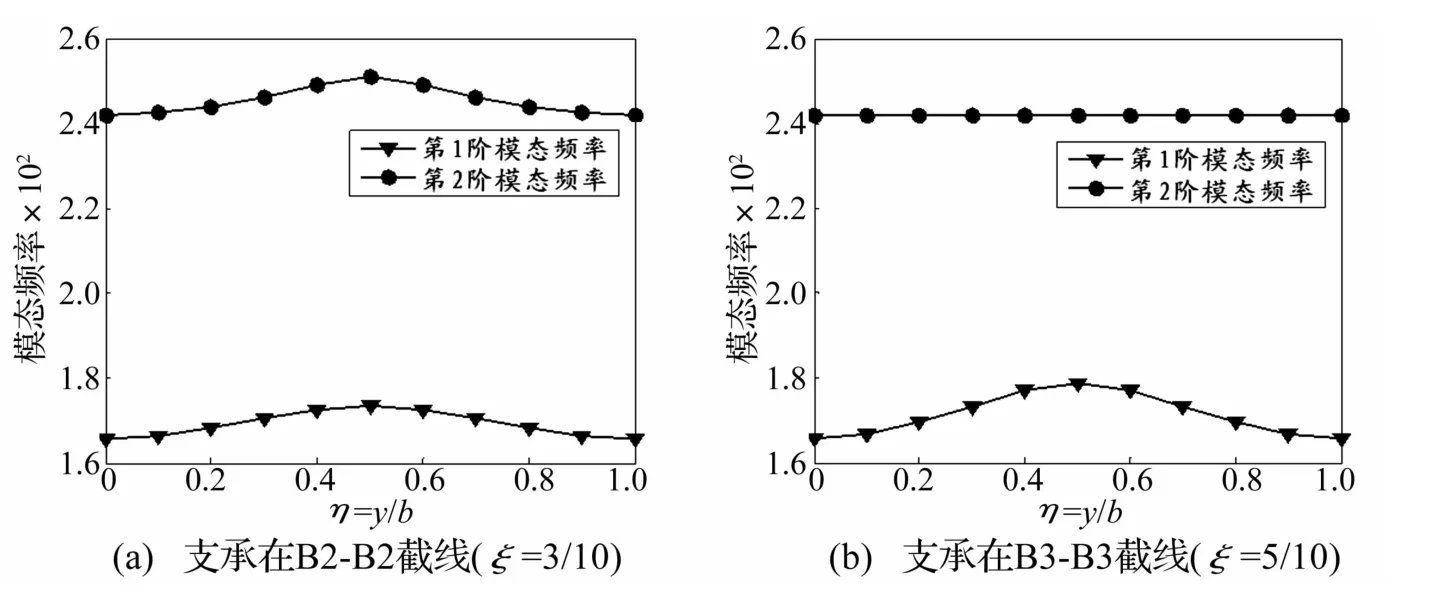
圖9 模態頻率隨支承位置的變化Fig．9 Modal frequency vs elastic support position

圖10 顫振動壓隨支承剛度的變化趨勢Fig．10 Dynamic pressure vs elastic support position

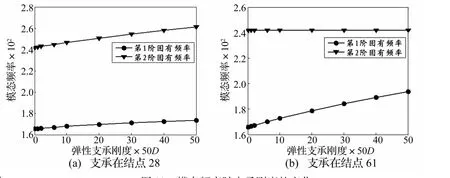
圖11 模態頻率隨支承剛度的變化Fig．11 Modal frequency vs elastic support stiffness

這是由于集中彈性支承位于曲壁板中線上時，只改變結構的第1階模態頻率，而對第2階模態頻率沒有影響，如圖9（b）所示。隨著支承向曲壁板中點移動，第1階模態頻率提高，而第2階模態頻率沒有變化，依據顫振的頻率重合理論，前兩階模態頻率更為接近，該兩階模態的耦合更容易使曲壁板發生顫振失穩，因而曲壁板的顫振動壓降低。

3.2 彈性支承剛度對曲壁板顫振動壓的影響

圖10為考慮附加彈性支承在曲壁板不同結點位置時，改變附加彈性支承剛度對曲壁板顫振動壓的影響，并與無彈性支承時曲壁板的顫振動壓進行比較。

從圖10可以看出，當曲壁板沒有附加彈性支承時（對應支承剛度為0），曲壁板的無量綱顫振動壓為323．3。當支承在順氣流方向靠近曲壁板中心附近區域時（如圖中結點50、61），隨著彈性支承剛度的增大，曲壁板的顫振動壓減小，而當支承在順氣流方向遠離曲壁板中心附近區域時（如圖中結點17、28、39），隨著彈性支承剛度的增大，曲壁板的顫振動壓隨之增大。

從彈性支承位于兩個不同的代表性位置（結點28、61）處的模態頻率隨剛度變化的趨勢進行分析，可以解釋這個現象。如圖11（a）所示，彈性支承位于結點28處時，隨著支承剛度的增大，前兩階模態頻率均呈增大的趨勢，但第2階模態頻率的增幅更大，即前兩階模態頻率之差隨著支承剛度的增大而增大，根據顫振的頻率重合理論，曲壁板的顫振動壓得到提高。如圖11（b）所示，彈性支承位于結點61處時，由于結點61為曲壁板第1階模態的節點，隨著剛度的增大，彈性支承對第2階模態頻率沒有影響，而第1階模態頻率隨之增大，即前兩階模態頻率逐漸靠近，根據顫振的頻率重合理論，曲壁板的顫振動壓會減小。

4 結 論

本文提出了一種在四邊簡支曲壁板上附加一個彈性支承來提高曲壁板顫振臨界動壓的方法，研究了彈性支承的位置和剛度對曲壁板顫振速度的影響規律，應用頻率重合理論分別分析了改變彈性支承剛度和位置對曲壁板顫振特性的影響。在工程實際中采用增加彈性支承的方式來改善曲壁板的顫振穩定性時，還需要解決如下一些問題：彈性支承的具體實現；彈性支承位置的精確確定以及與壁板連接；彈性支承材料的選擇；彈性支承本身質量的影響。目前的研究是為這一技術途徑的工程實現提供理論上的參考。本文的研究結果表明：

（1）彈性支承位于曲壁板中心點附近區域或位于弦向中線上時，都會導致曲壁板顫振動壓降低且隨著支承剛度的增大而減小；在曲壁板中心點處，顫振動壓降低幅度最大；

（2）彈性支承位置沿垂直于氣流方向且遠離弦向中線變化時，都會使顫振動壓提高，且隨著支承剛度的增大而增大；

（3）當支承位置在前緣和后緣部位順氣流方向變化時，顫振動壓都會提高；

（4）采用附加彈性支承的方法來提高曲壁板顫振動壓時，應將彈性支承布置在曲壁板展向中線距邊界約20%弦長處。

本文得到的彈性支承對曲壁板顫振特性影響的定性規律，適用于其他尺寸及構型的曲壁板和平壁板，只是具體的最佳彈性支承大小和位置不同。本文的研究是在顫振頻率重合理論的基礎上開展的，從不同彈性支承下的模態節線變化，即模態耦合的角度來研究彈性支承對曲壁板顫振穩定性的影響，是后續要開展的工作。

［1］Plaut R H．Structural optimization of a panel flutter problem［J］．AIAA Journal，1971，9（1）：182－184．

［2］Pierson B L．Aeroelastic panel optimization with aerodynamic damping［J］．Technical Notes，1975，13（4）：515－517．

［3］ Dowell E H．Nonlinearflutter of curved panels［J］．AIAA Journal，1969，7（3）：424－431．

［4］Azzouz M S，Guo X，Przekop A，et al．Nonlinear flutter of cylindrical shell panels under yawed supersonic flow using FE［C］．AIAA 2004－2043，45th AIAA／ASME／ASCE／AHS／ASC Structures， Structural Dynamics and Materials Conference，Palm Spring，CA，2004．

［5］ Azzouz M S，Mei C．Nonlinearflutter of cylindrical panels under yawed supersonic flow using finite elements［C］．AIAA 2005 － 2373， 46th AIAA ／ASME ／ASCE ／AHS／ASC Structures，Structural Dynamics and Materials Conference，Austin，Texas，2005．

［6］Azzouz M S．Nonlinear flutter of curved panels under yawed supersonic flow using finite elements［D］． Ph．D．Dissertation，Old Dominion University，Norfolk，VA，2005．

［7］張蕊麗，楊智春．曲壁板在超音速氣流中的分岔特性［J］．力學學報，2010，42（5）：863－869．ZHANG Rui-li，YANG Zhi-chun．Bifurcation of the curved panel in supersonic air flow ［J］． Chinese Journal of Theoretical and Applied Mechanics，2010，42（5）：863－869．

［8］楊智春，周建．谷迎松．超音速氣流中受熱曲壁板的非線性顫振特性［J］．力學學報，2012，44（1）：30－38．YANG Zhi-chun， ZHOU Jian， GU Ying-song． Nonlinear thermal flutter of heated curved panels in supersonic air flow［J］．Chinese Journal of Theoretical and Applied Mechanics，2012，44（1）：30－38．

［9］Krause H，Dinkler D．The influence of curvature on supersonic panel flutter［C］．AIAA 98－1841，1998．