二自由度行波型超聲波電機的軌跡控制

傅 平，胡錫幸，郭吉豐

（1，福州大學 電氣工程學院，福州 350108；2，閩江學院 物理學與電子信息工程系，福州 350121；3，國網浙江省電力公司杭州供電公司，杭州 310009；4，浙江大學 電氣工程學院，杭州 310027）

二自由度球形超聲波電機低速大力矩、定位精度高的特性非常適合做多自由度機器人的執行機構。但是二自由度超聲波電機［1－9］具有非線性、時變、強耦合的特性，使得它的轉速、位置檢測比較困難。目前，國內外關于二自由度球形超聲波電機性能測試的報道較少。

二自由度球形超聲波電機的輸出變量主要是轉速、位置。目前在二自由度球形超聲波電機中最常用的位置檢測機構［4］如圖1所示，在電機的x軸和y軸方向上分別安裝光電編碼器，在每個編碼器的軸上安裝一個圓弧帶槽框架，球轉子輸出軸通過兩條圓弧帶槽框架的相交點。通過兩個編碼器所測得的轉角就能得到輸出軸的空間位置。這種檢測方式需要在球轉子上安裝一個輸出軸，轉子的運動范圍會受到限制。文獻［10］給出了轉速和電壓的關系圖。文獻［11］給出了電機繞各軸的最高轉速，但其輸出轉矩因太小而難以檢測。文獻［12］給出了多自由度球形超聲波電機的空載轉速和最大輸出轉矩。文獻［13］使用調心軸承和連桿機構來檢測球轉子姿態角，其運動范圍仍受制約。除此之外則是采用視覺識別測量系統，在球轉子表面噴涂網格圖，并從中提取特征點以識別網格的位置。Lee等［13］使用雙光學傳感器在2個方向檢測球轉子的表面變化量，進而測量出球體三自由度的運動姿態。采用光學傳感器有助于提高檢測精度，但是增加了控制系統的運算量。Mashimo等［14］提出用激光檢測球轉子的位置，激光的應用進一步提高了檢測精度，但也使得成本提高以及檢測范圍受限。

圖1 常用的位置檢測機構Fig．1 Position detectingmechanism in common use

二自由度球形超聲波電機［15］是通過3個定子的相互協調控制來實現球轉子的運行，因此研究球轉子在單個定子不同頻率、相位、幅值以及驅動方式（駐波、行波）下的運行特性是分析二自由度球形超聲波電機的基礎。實驗中，首先進行單定子驅動球轉子特性的測試。測試系統采用光電編碼器測定球轉子轉速，轉矩測試模塊測量球轉子的輸出力矩，并通過壓緊螺母調整加載預緊力的大小。最后再進行二自由度球形超聲波電機的軌跡控制。

1 單定子電機的輸出特性

電機轉速和驅動頻率的對應關系如圖2（a）所示。從圖中可以知道，電機的穩定工作區一般選取在諧振點右側一段較小的區間，該區間帶寬大約為400 Hz，即49．1－49．5 kHz。在工作區間內對應的機械特性如圖2（b）所示，可以看到隨著驅動頻率的增加，電機空載轉速和堵轉力矩都有所下降。

圖3是電機轉速隨相位差的變化曲線。從圖3可以看到，定子兩相輸入電壓的相位差在過零點附近存在一個轉速死區。當驅動頻率為49．2 kHz時，死區約為 ±20°。

圖4是電機轉速隨輸入電壓變化曲線。圖中可以看到輸入電壓與轉速之間存在一個死區，只有當輸入電壓的峰峰值超過30 V后，轉子才開始運轉。

圖2 頻率－速度特性Fig．2 Speed-driving frequency characteristics

2 軌跡運行控制

對于2自由度超聲波球電機而言，平面任意方向的角速度ω都可以通過兩個相互垂直的角速度ω1、ω2合成，如圖5所示。

圖5 角速度分解Fig．5 Decomposition of angular velocity

圖3 轉速－相位差特性Fig．3 Speed-driving phase-difference characteristics

圖4 轉速－輸入電壓特性Fig．4 Speed-input voltage characteristics

圖5中β表示ω1與ω之間的夾角，它們的關系為

2自由度球形超聲波電機包含3個定子，空間呈120°對稱分布［15］。假設3個定子表面行波波峰點沿定子周向的角速度分別為 ωs1，ωs2，ωs3，可以得到 ωs1，ωs2，ωs3與 ω1和 ω2之間滿足

上式中nx和ny分別為x和y軸的單位向量。

由式（1）、（2）和（3），并以極小范數解作為優化目標，冗余性及其控制策略具體見文獻［15］。當控制球轉子的空載轉速在單位圓內時，可以得到ωs1、ωs2、ωs3滿足以下關系

其中k是常數，滿足

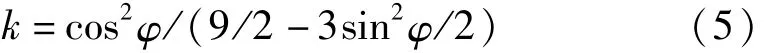
式（5）中 φ＝arccos（r／R），r是定子有效半徑，R是球轉子半徑。

因此，通過配置3個定子表面的角速度就能完成轉子在x，y坐標軸內沿任意角度運行。

2.1 轉速控制方法

通過合理配置定子表面的角速度就能完成轉子在x，y坐標軸內沿任意角度運行。而定子表面的角速度可以通過改變定子輸入電壓的頻率、幅值和相位差進行調整。由單定子電機的輸出特性可以知道主要有以下幾種方法實現：

（1）調頻控制

調頻控制是最常用的控制方式，但是2自由度球形超聲波電機通過調諧實現三個定子的諧振頻率一致。通過調頻調速，電機輸入頻率一旦遠離諧振區，就會產生較大的轉速波動，影響電機的控制效果。因此不適合采用調頻的方式進行控制。

（2）調壓控制

調壓控制可以實現定子振幅的平穩變化。對于超聲波電機而言，調壓控制可調節的范圍較小。

（3）相位差控制

采用相位差控制可以實現電機轉速大小和方向的平穩調整。對于電機而言，相位差控制在降低電機轉速的同時，不會帶來負載轉速的增加。因此運行過程中，通過改變相位差對電機進行轉速調整，可以在調速時保證電機平穩運行。為了確定單個定子驅動時電機轉子轉速和定子兩相相位差之間的對應關系，需要對圖3的數據進行擬合。由圖3可以看出電機轉速和相位差之間呈現較強的非線性關系，大大增加了實際控制過程的運算量。通過分段線性擬合，可以得到電機轉速n與定子兩相相位差θ之間的對應關系

單定子驅動時相位差θ與轉速n對應關系的實測點與式（6）擬合曲線的對比如圖6所示，從圖中可以看到擬合曲線和實際測試點基本接近，能夠反映電機轉速隨相位差的變化規律。

聯立式（4）和（6），并采用歸一化處理，可以得到β與定子1相位差θ1之間滿足

圖6 定子相位差與轉速對應關系Fig．6 Relation between speed of rotor and phase difference of each stator

其中nmax＝300 r／min。同理 θ2和 θ3也可以通過同樣的方法得到。通過式（7）以及定子相位差的對應關系，可以得到β與各個定子的對應關系如圖7所示。由圖7可以看到，定子相位差θ與β角的對應關系并不連續，這是由于調相時電機存在運行死區。

2.2 驅動控制系統

2自由度超聲波電機驅動控制系統由PWM控制電路、驅動電路、位置檢測和信號處理電路這四部分構成。其中PWM控制電路主要完成反饋信號的采集，以及PWM波形的輸出。驅動電路通過光耦和推挽電路將PWM信號放大并驅動電機運轉。位置檢測把球轉子的旋轉角度通過光柵轉化為正弦信號輸出。信號處理電路將光電編碼器輸出的信號濾波、放大、整形，使電機的位置輸出信號能被控制電路采集。

（1）PWM控制電路

PWM控制電路采用TI公司的TMS320F28335作為PWM發生和反饋信號采集的控制芯片。

（2）驅動電路

驅動電路將PWM信號放大，輸入到推挽電路中，再對電機進行阻抗匹配，關于驅動電路，可參考文獻［13］，這里就不再作相應介紹。

（3）位置檢測

電機的位置檢測包括電機本體、柵輪、膠質滾球等組成，如圖8所示。位置檢測機構上的碼盤齒數n＝45，碼盤細桿直徑d＝2 mm，球轉子直徑D＝40 mm。因此位置檢測機構x、y兩個方向上的精度δ可以達到

光電信號輸出電路輸出四路方波，通過測量方波信號及其順序就可以得到電機轉子的相應位置。

圖8 檢測機構示意圖Fig．8 Diagram of detection mechanism

（4）信號處理電路

光電編碼器輸出方波信號，幅值只有1 V左右，而且還伴隨著大量的諧波干擾。為此需要對信號進行放大、濾波和整形。電路如圖9所示。

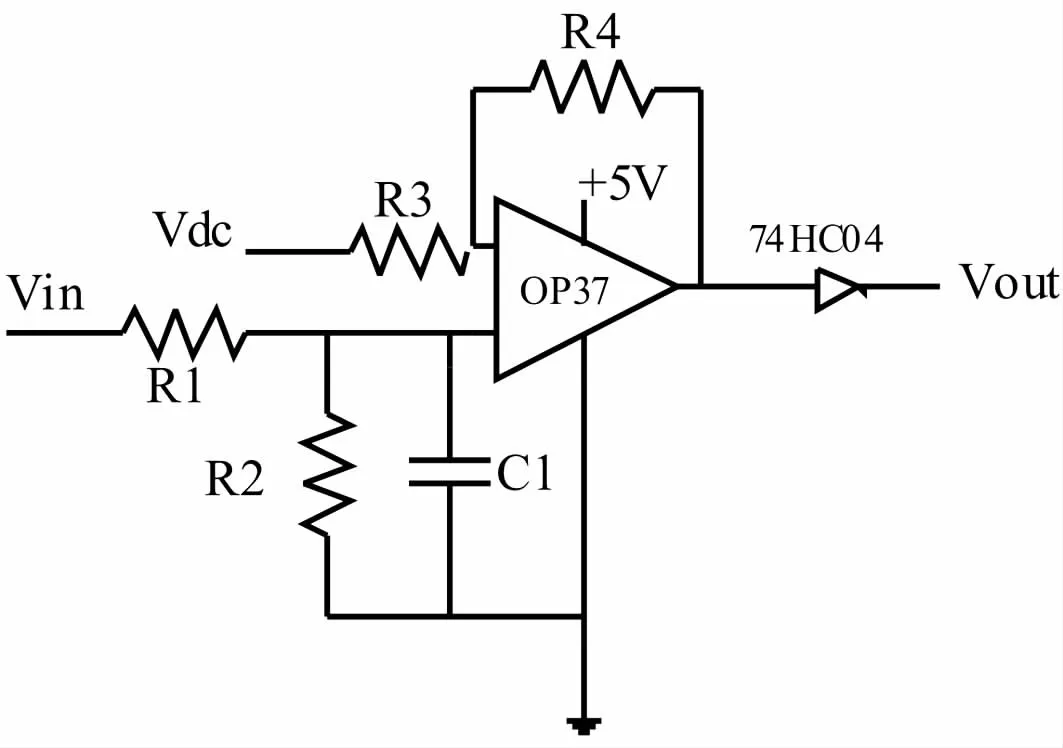
圖9 信號處理電路Fig．9 Circuit of signal processing

若只采用相位差控制，當β為60°時，3個定子兩相的相位差分別為45°、45°和 －90°。圖 10（a）是 x軸和y軸編碼器的運行轉速。從圖10（a）可以看到，編碼器運行較為平穩，其中x軸編碼器的轉速波動在8．5%以內，而y軸的轉速波動在5%以內。通過x軸和y軸編碼器的轉速可以得到β的實際值。圖10（b）是β的設定值和實際值，可以看到β設定值和實際值之間最大相差 8°。

表1是設定β后對應的3個定子的角速度ωs1、ωs2、ωs3的比例關系和每個定子的相位差。圖11是設定β和3個定子兩相的相位差后電機的開環運動軌跡。

實驗時，球轉子的運動姿態用轉子表面某點的運動軌跡描述，為簡單起見，具體的運動位置直接采用光電編碼器的脈沖數表示，如設定沿直線運動，直線的邊界位置分別為（60，100），（－60，100），（－60，－100）和（60，－100），實際運動軌跡如圖11所示，圖中虛線表示設定軌跡，實線為電機實際運行軌跡。由圖11可以得到，不同β下實際運行軌跡與設定值之間存在一定誤差，其中β為60°時，誤差較大，達到8°；β為180°時，誤差較小，只有4°。

圖10 轉速與β情況Fig．10 Speed and changing ofβ

表1 不同β下定子1、2、3的相位差Tab．1 Phase-difference of stator 1、2、3 with differentβ

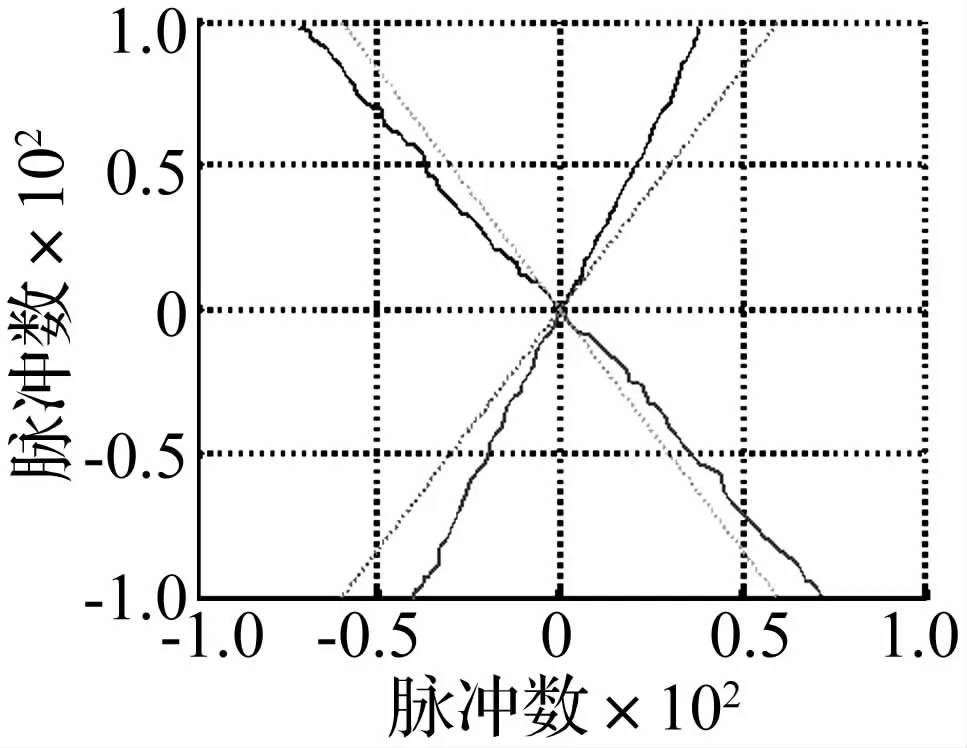
圖11 電機開環運動軌跡Fig．11 Trajectory ofmotion by open loop control

2．3 閉環控制方法

從前面的結果可以知道，開環控制中β誤差較大。對于軌跡控制而言，需要對電機進行閉環控制，才能實現良好的軌跡跟蹤。

圖12 軌跡閉環控制原理圖Fig．12 Diagram of trajectory by closeloop control

如圖12所示，假設電機轉子上某點初始位置為O，目標位置設為P，通過前面的結果可以知道，使用開環控制達不到理想的控制效果，為此采用分段逐點比較法來實現電機的軌跡控制。

假設在初始位置，O點與電機圓心重合，運行到目標位置P所對應的運動矢量與x軸的夾角為β。通過式（7）可確定3個定子的兩相相位差。由于開環控制的誤差，當電機運行到P1點，其中圓心到P1點與x軸的夾角為 α1，則

當e（k）≤0，需要減少轉子運動矢量與x軸之間的夾角，并通過式（7）確定各定子的兩相相位差。當e（k）＞0時，需要增加轉子運動矢量與x軸之間的夾角，并通過式（7）確定各定子的兩相相位差。當目標位置P坐標與電機實際運動位置Pi坐標符合（ε為設定閾值）時認為電機到達指定位置，完成閉環軌跡控制。

由于超聲波電機運行時存在一定的非線性，傳統的PID控制效果較差，我們采用了文獻［16］的神經元PID算法對電機進行控制。神經元學習控制所需要的狀態量為 x1（k）、x2（k）、x3（k）。這里，x1（k）、x2（k）、x3（k）分別定義為

神經元輸出u（k）

上式中 k為神經元的比例系數，k＞0，w1（k）、w2（k）、w3（k）為神經元對 x1（k）、x2（k）、x3（k）的權重系數。權重系數的調整規則見文獻［16］。

通過式 （11）和式（7）相位差的計算公式可以求得電機兩相的相位差，對應的主程序流程如圖13所示。

3 實驗結果分析

由于電機運行過程中容易產生位移抖動現象，會產生較大的誤差變化率，因此在神經元PID控制算法里假定w3＝0，即采用PI調節。

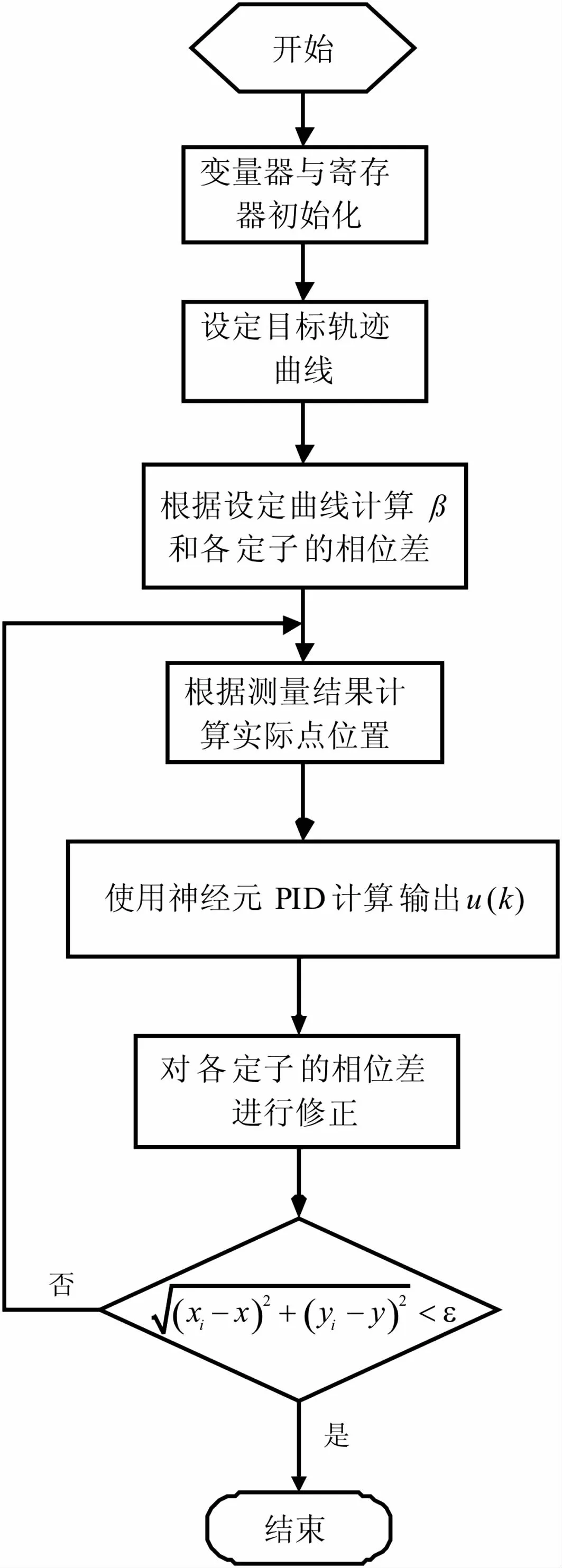
圖13 主程序流程圖Fig．13 Themain program flow chart of software

圖14是閉環控制下β與相位差的變化情況，其中β設定為60°。從圖14（a）可以看到，閉環控制下，穩定后的β為59．88°，穩定時間大約為0．8 s。其中各定子兩相相位差的變化情況如圖14（b）所示。隨著時間的增加，定子1兩相相位差先增大后減少，定子2兩相相位差先減少后增加，定子3兩相相位差基本保持不變。

圖14 電機閉環運行情況Fig．14 Case when closeloop control

圖15是設定目標位置后電機的閉環控制曲線。從圖中可以看到，在閉環控制中，電機運行曲線基本上能夠跟蹤設定曲線，從而實現較好的軌跡跟蹤控制。

圖15 閉環控制曲線Fig．15 Trajectory ofmotion when closeloop control

表2是軌跡閉環控制時的情況。從表2可以看出，閉環控制下電機x軸和y軸的脈沖位置誤差控制分別控制在2個脈沖以內，由于我們使用的碼盤齒數較少，使得對應x軸和y軸的角度誤差絕對值在0．8°以內。若使用碼盤齒數更多的編碼器，則可以達到更高的精度。

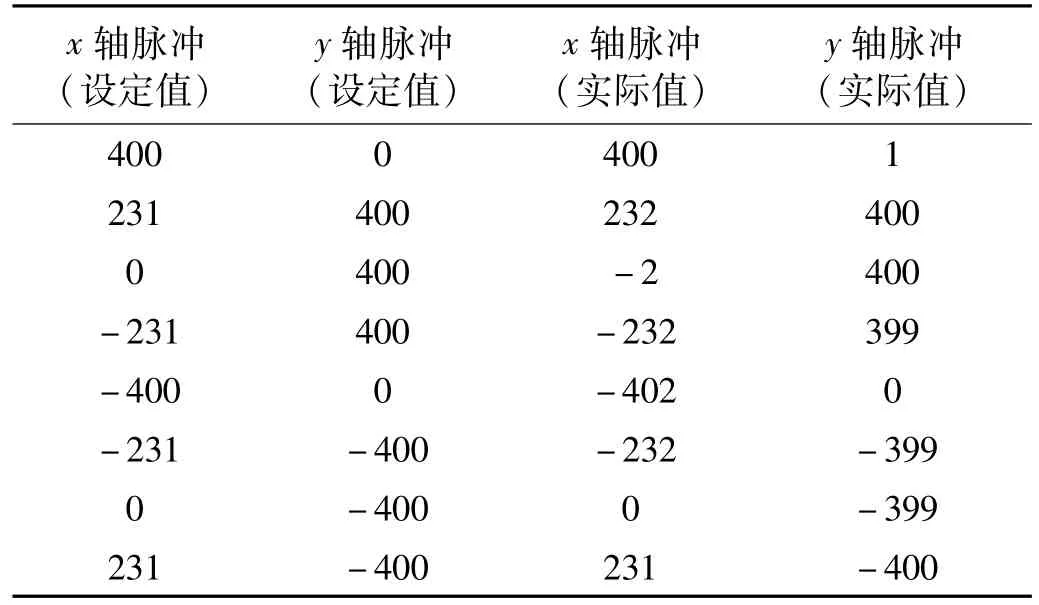
表2 閉環控制情況Tab．2 Closeloop control

若設定電機沿四邊形直線運動，四邊形的位置（以脈沖計數）分別為（－100，－100），（100，－100），（100，100），（－100，100），電機運動時實際的位置分別為（－99，－98），（99，－98），（99，99），（－98，98），得到的實際運動軌跡如圖16所示。圖中可以看到實際運動軌跡的位置誤差控制在2個脈沖以內，誤差不超過2%，可實現較好的軌跡跟蹤。

圖16 四邊形軌跡Fig．16 Quadrilateral trajectory ofmotion

4 結 論

本文通過分析轉子運動矢量和x軸夾角β與定子相位差的對應關系，提出了一種二自由度超聲波電機的軌跡控制策略。實驗證明使用神經元PID控制方法對電機實行軌跡閉環控制后，電機運行曲線對應的x軸和y軸的角度誤差控制在2個脈沖以內。

本文提出的軌跡控制方法不僅為多自由度超聲波球電機的姿態控制奠定了基礎，而且為多自由度超聲波球電機的位置／速度伺服研究提供了一種思路。

［1］郭吉豐，傅平．多自由度球形超聲波電機的研究進展［J］．電工電能新技術．2005，24（2）：65－68．GUO Ji-feng，FU Ping．The research progress ofmulti-degree of freedom ultrasonic motor［J］．Adv．Tech．of Elec．Eng．＆Energy，2005，24（2）：65－68．

［2］Mashimo T，Awaga K，Toyama S．Development of a spherical ultrasonic motor with an attitude sensing system using optical fibers［J］．IEEE Inter．Conf．on Robotics and Automation，2007：4466－4471．

［3］Purwanto E，Toyama S．Developmentof an ultrasonicmotor as a fine orienting stage［J］．IEEE Trans on Robo．and Auto．，2001，17（4）：464－471．

［4］Shigeki T，Zhang Guo-qiang，Osamu M．Development of new generation spherical ultrasonic motor［C］．Proc．of the 1996 IEEE Inter． Conf． on Robotics and Automation．Minneapolis，1996，3：2871－2876．

［5］河井元良．超音波リニアアクチユエ一ㄆを用いた三自由度球面モ一ㄆの研究［J］．精密工學會志，1993，60（3）：405－410．Motoyoshi Kawai．Research of aspherical motor with 3 DOF driven by ultrasonic linear actuators［J］．JSPE，1993，60（3）：405－410．

［6］佐佐江啟介．3自由度小型アクユエ一ㄆの開發（第3報）［J］．精密工學會志，1996，62（4）：599－603。Keisuke Sasue．Development of a small actuator with 3 DOF［J］．JSPE，1996，62（4）：599－603．

［7］AoyagiM，Beeby SP，White N M．A novelmulti degree of freedom thick-film ultrasonic motor［J］．IEEE Transactions on Ultrasonics，Ferroelectrics and Frequency Control，2002，49（2）：151－158．

［8］Chen Qiang， Hu Min-qiang， Jin Long， et al． Force transmission model of a cylindrical linear ultrasonic motor［C］．Proceeding of International Conference on Electrical Machines and Systems 2007，Oct．8－11，Seoul，Korea：1623－1628．

［9］Takemura K，Maeno T．Design and control of an ultrasonic motor capable of generating multi-dof motion［J］．IEEE／ASME Transactions on Mechatronics，2001，6（4）：499－506．

［10］胡錫幸，郭吉豐，傅平，等．2自由度球形行波型超聲波電動機的特性計算模型［J］．機械工程學報，2009，45（3）：229－233．HU Xi-xing， GUO Ji-feng，FU Ping，et al． Mechanical characteristics calculation of 2DOF spherical traveling-wave ultrasonic motor［J］．Journal of Mechanical engineering，2009，45（3）：229－233．

［11］傅平，郭吉豐，沈潤杰，等．二自由度行波型超聲波電機的驅動和運動姿態控制［J］．電工技術學報，2008，23（2）：25－30．FU Ping，GUO Ji-feng，SHEN Ren-jie，et al．Driving circuit and position control system of two degree of freedom spherical travelingwave type ultrasonicmotor［J］．Transactions of China Electrotechnical Society，2008，23（2）：25－30．

［12］傅平，郭吉豐，沈潤杰．球形行波型超聲波電機的驅動數學模型［J］．中國電機工程學報，2006，26（23）：115－119．FU Ping，GUO Ji-feng，SHEN Run-jie．The drivingmathematic model of spherical traveling-wave type ultrasonic motor［J］．Proceedings of CSEE，2006，26（23）：115－119．

［13］ Lee K M，Zhou De-bao．A real-time optical sensor for simultaneousmeasurementof three-DOFmotions［J］．IEEE／ASME Transactions on Mechatronics，2004，9（3）：499－507．

［14］Mashimo T，Awaga K，Toyama S，Developmentofa spherical ultrasonic motor with an attitude sensing system using optical fibers［C］．2007 IEEE Inter．Conf．on Robotics and Auto．，Roma，Italy，April 10－14，2007，4466－4471．

［15］胡錫幸，郭吉豐。3個行波定子的2自由度球形超聲波電機［J］．中國電機工程學報，2010，30（9）：62－67．HU Xi-xing，GUO Ji-feng．Two degree of freedom spherical ultrasonic motor with three traveling-wave stators［J］．Proceedings of the CSEE，2010，30（9）：62－67．

［16］傅平，郭吉豐，丁敬，等．基于神經元自適應PID的超聲波電機速度位置控制［J］．電工技術學報，2007，22（2）：28－33．FU Ping，GUO Ji-feng，DING Jin，et al．A neuron adaptive PID-based speed and position control for ultrasonicmotor［J］．Transactions of China electrotechnical society，2007，22（2）：28－33．