某新型多身管火炮的膛口流場形成分析

陳偉,王茂森,戴勁松,陳瑤

(1.南京理工大學機械工程學院,江蘇南京210094;2.南京軍區聯勤部信息中心江蘇南京210016)

0 引言

根據文獻[1]中關于雙股射流的闡述,齊射時,其流場包含會聚區和聯合區,兩股射流之間存在負壓。而多身管火炮膛口流場又有別于一般的多股射流,主要是由于膛口流場中包含了高速運動的彈丸。在彈丸剛離開炮口時,膛口火藥燃氣高速噴出,與彈底的作用可近似為沖擊射流來分析,隨著時間推進,彈丸的影響漸小。而后繼發射的彈丸在穿越膛口流場的過程中將破壞已形成的流場結構,其發射產生的火藥燃氣射入膛口流場時,也將產生疊加作用,影響膛口流場的發展特性;改變后的膛口流場又反過來作用于彈丸,影響彈丸的運動狀態。它們之間是相互耦合作用的關系。因此,后繼發射的彈丸進入膛口流場的時機以及入口位置將直接決定膛口流場的發展與彈幕散布情況。綜上所述,結合多身管火炮的結構特點,分析認為射速、身管間距以及射擊時序是影響多身管火炮以高射速進行連發射擊的膛口流場的主要因素。雙股射流的相關研究表明,流場的結構及氣流參量分布受兩孔間的距離影響很大。為此,針對雙身管在高射速度條件下射擊的情況,文中將通過仿真比較不同身管間距對膛口流場發展的影響。對帶300 mm測速裝置的雙身管在齊射、間隔0.3 ms發射、間隔0.6 ms發射條件下進行仿真計算,兩身管間距分別取為120 mm和180 mm。

1 數學模型

1.1 基礎物理模型

流體的連續介質假設適用于本文所開展的膛口流場分析,其運動規律滿足質量守恒、動量守恒和能量守恒定律,分別體現為連續性方程、動量方程和能量方程。

連續性方程的表達式為:

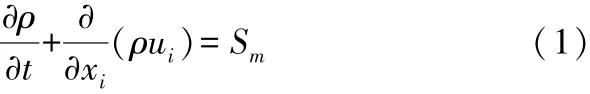
式中:ρ為流體密度;xi表示坐標;ui為速度分量;Sm為源項,是稀疏相加入到連續相中的質量。

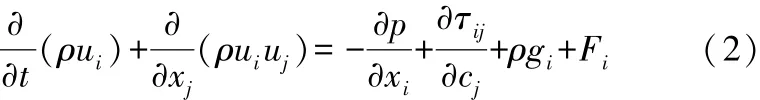
動量方程的表達式為:式中:p為靜壓;τij為應力張量;ρgi和 Fi分別為 i方向上的重力體積力和外部體積力。對于應力張量,有:

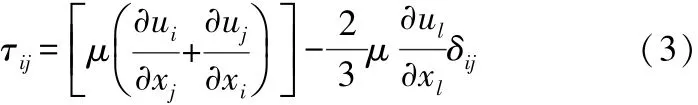
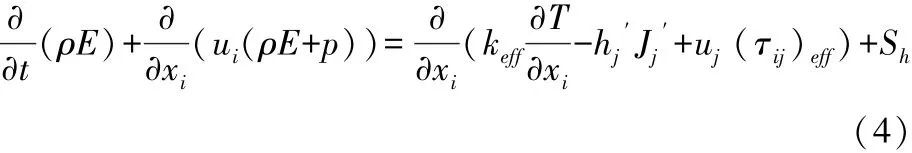
能量方程的表達式為:式中:keff＝kt＋k,為有效導熱系數;Jj′是組分 j′的擴散通量;Sh是包括化學反應熱和其他體積熱源的源項。其中:

膛口流場為可壓縮流動,焓定義為:

其中,是組分′的質量分數。組分j′的焓定義為:

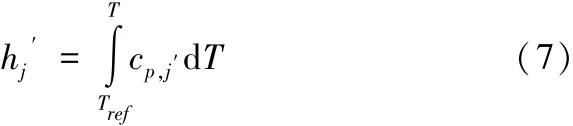
其中,Tref＝298.15K。

1.2 湍流模型

根據火炮膛口流場的特點,應用基于湍流動能和擴散率的標準k－ε模型進行模擬是合適的[2]。k方程是個精確方程,ε方程是個由經驗公式推導得到的方程,其表達式為:

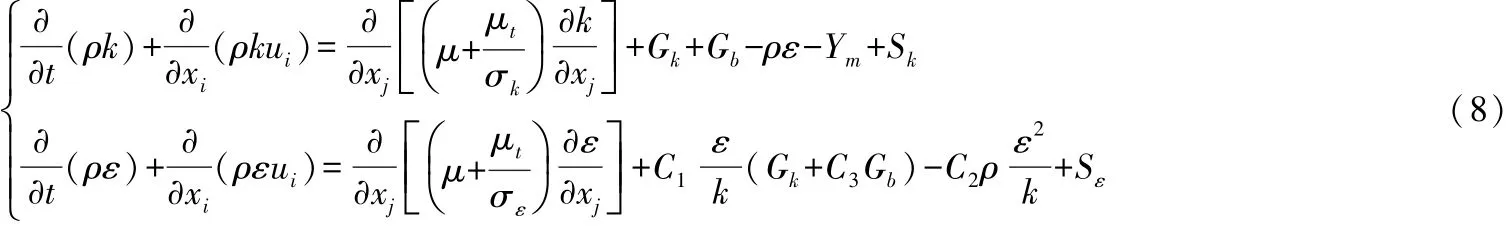
式中:Gk為由層流速度梯度引起的湍流動能;Gb為由浮力引起的湍流動能;Ym為湍流過渡的擴散產生的波動;σk和σε分別是k方程和ε方程的湍流Prandtl數;C1、C2、C3為系數;

湍流黏性系數為:

湍流動能的表達式為:

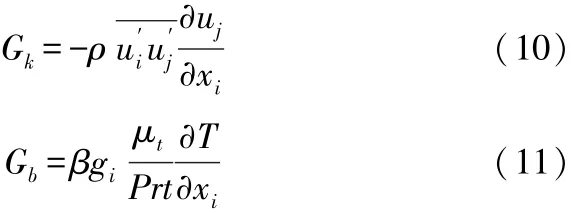
式中:Prt為能量的湍流普特朗數。

熱膨脹系數為:

膛口流場屬于高馬赫數流動問題,可壓縮性對湍流的影響在YM中體現:

其中,Mt是馬赫數,定義為:

其中,T是聲速。

根據經驗確定:Cμ＝0.09,C1＝1.44,C2＝1.92,σk＝1.0,σε＝1.3。而C3按如下函數變化:

其中,v是平行于重力方向的速度分量;u是垂直于重力方向的速度分量。

1.3 彈丸運動方程

為研究彈丸的空間運動,建立坐標系如圖1所示:地面坐標系 O－xyz,平動坐標系 O′－xdydzd,彈道坐標系O′－x2y2z2、 彈 軸 坐 標 系 O′－ ξηζ和 彈 體 坐 標 系O′－ξ1η1ζ1[3]。

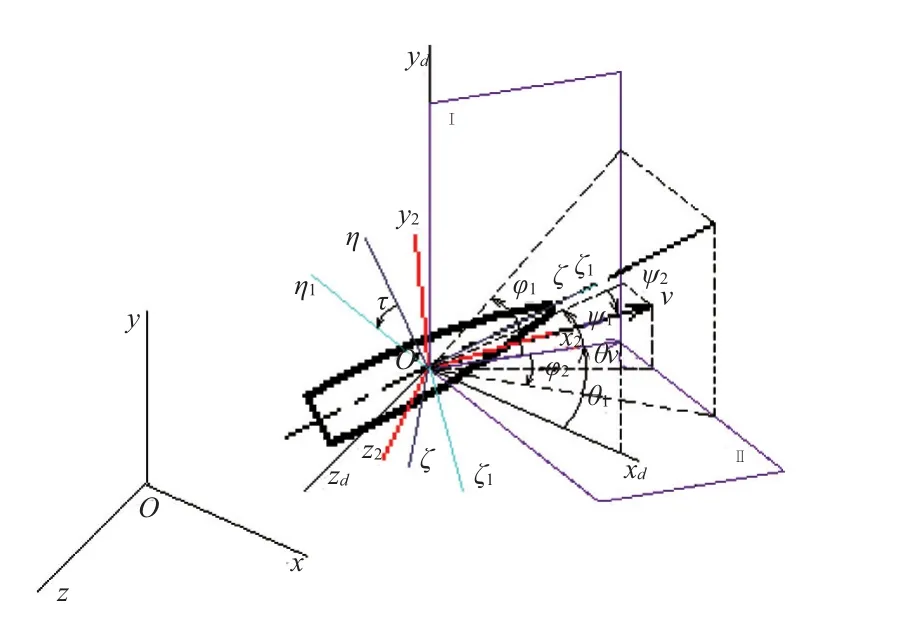
圖1 彈丸運動坐標系

圖1中:v為彈丸速度;vH為理想彈道的切線方向;平面Ⅰ為過vH的鉛垂面;平面Ⅱ為過vH且垂直于平面Ⅰ的平面;θ為彈道傾角;θ1為理想彈道對應的彈道傾角;ψ1為彈道傾角相對理想彈道傾角的一個增量,通常為小量;ψ2為側向偏角;φ1為彈軸在鉛垂面內相對于理想彈道的彈道傾角方位的轉角;φ2為彈軸在平面Ⅱ內相對于理想彈道的側向偏角;γ為自轉角。

彈丸在穿越多身管膛口流場過程中受到的力和力矩包括:重力G、火藥燃氣作用力Fp、切向阻力Rx、升力Ry、馬格努斯力Rz、火藥燃氣作用力矩Mp、俯仰力矩Mz、極阻尼力矩Mxz、赤道阻尼力矩Mzz、馬格努斯力矩My等。由于膛口流場區域相對于整個外彈道而言很小,可忽略柯氏慣性力及柯氏慣性力矩的影響。對彈丸進行受力分析如圖2所示,圖中,δ為攻角。

根據外彈道理論,建立彈丸運動方程:

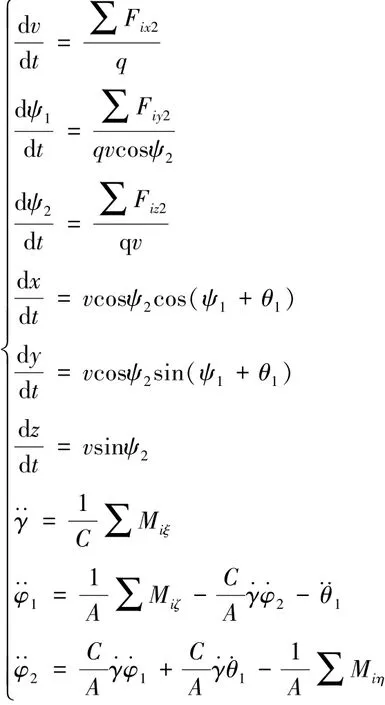
圖2 彈丸穿越膛口流場過程的受力情況

式中:q為彈丸質量;A為彈丸的赤道轉動慣量;C為彈丸的極轉動慣量。為作用于彈丸上的合力在彈道坐標系各軸上的投影;分別為作用在彈丸上的合力矩在彈軸坐標系各軸上的投影。有分析表明:氣動力相對火藥氣體作用力而言,對彈丸的作用力可忽略不計[4]。而本文為探索多身管膛口流場對后繼發射彈丸的影響,在進行數值模擬時,忽略了重力的影響,卻考慮了氣動力的作用;而在進行200 m立靶彈著點擬合分布時,則忽略了氣動力的影響,主要考慮重力的作用。

2 仿真三維模型的建立

圖3是該模型是利用Gambit畫圖軟件,先根據參數畫出一半,利用軸對稱進行旋轉而得。采用這種方式既可以更有效地以三維的模式展現仿真情況,也減少了三維模型仿真時的計算量。

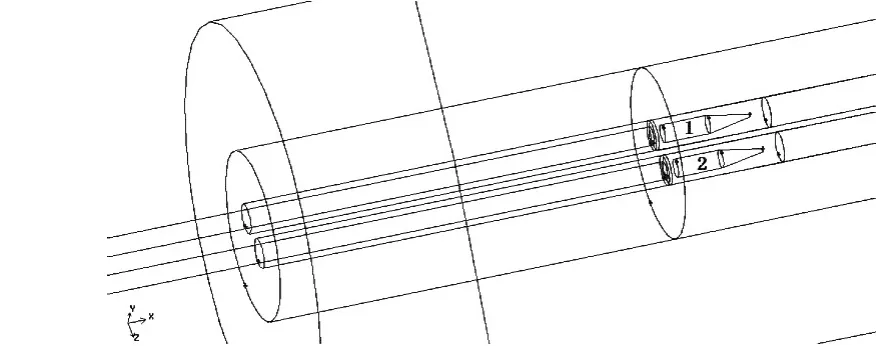
圖3 帶集束裝置的膛口流場三維仿真模型

3 仿真結果與分析

3.1 雙身管齊射

圖4和圖5是雙身管齊射時,膛口流場的靜壓圖和馬赫數分布圖。

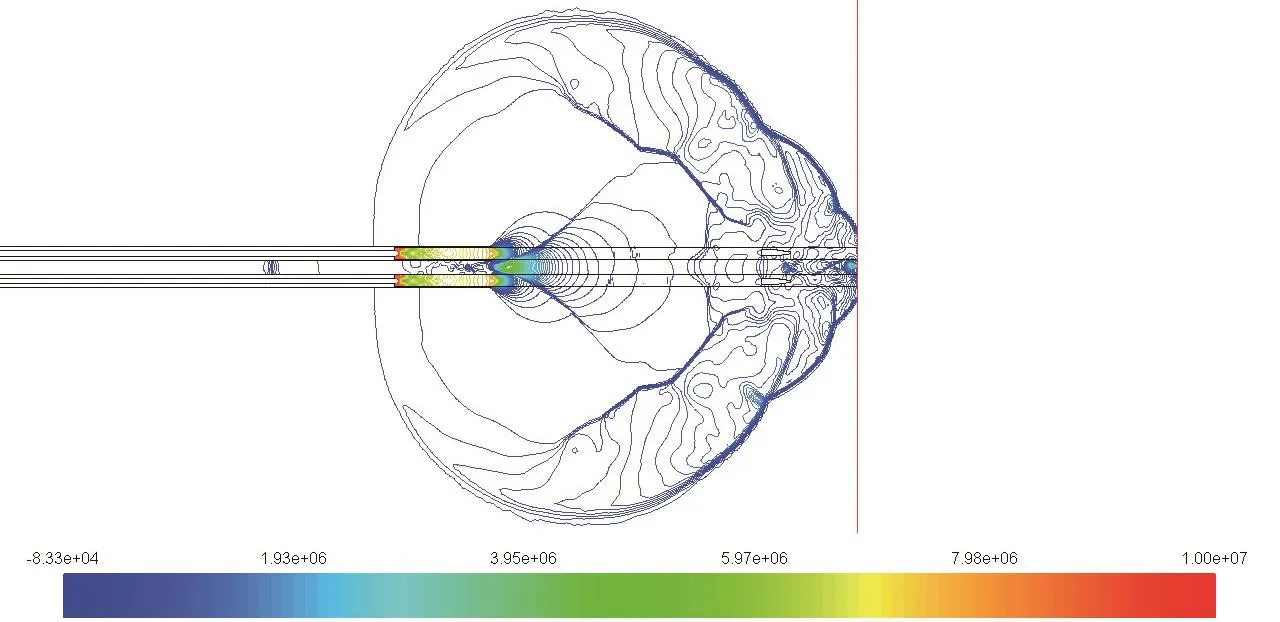
圖4 膛口流場靜壓圖

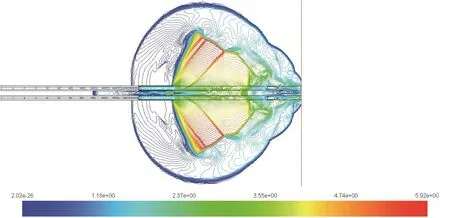
圖5 馬赫數分布圖

圖6和圖7所示為在不同身管間距條件下,雙身管齊射時,帶300 mm集束裝置的雙身管膛口流場仿真得到的彈丸1和彈丸2在穿越膛口流場過程中的軸向速度與徑向速度的變化情況。由仿真分析結果可知:當雙身管齊射時,膛口流場均表現出相似的特性,與身管間距無關。但隨著身管間距不斷加大,膛口流場對彈丸的作用有所減弱。這在軸向上表現不明顯,如圖6所示,彈丸軸向速為度變化1 m/s以內;而對彈丸徑向的影響則相對大得多,如圖7所示,兩身管間距60 mm時的彈丸徑向增速是間距180 mm時的2倍。

圖6 不同身管間距齊射時,彈丸穿越膛口流場的軸向速度變化情況

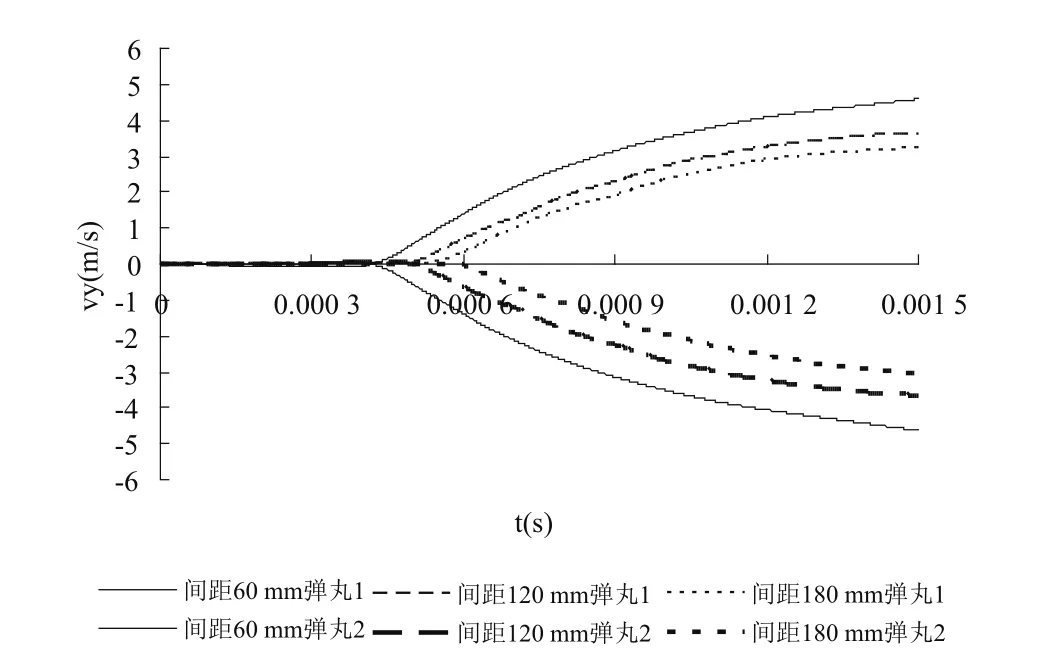
圖7 不同身管間距齊射彈丸穿越膛口流場的徑向速度變化情況

3.2 雙身管間隔發射

圖8和圖9為雙身管間隔發射時,仿真得到的膛口靜壓分布圖和馬赫數分布圖。

圖8 膛口靜壓分布圖

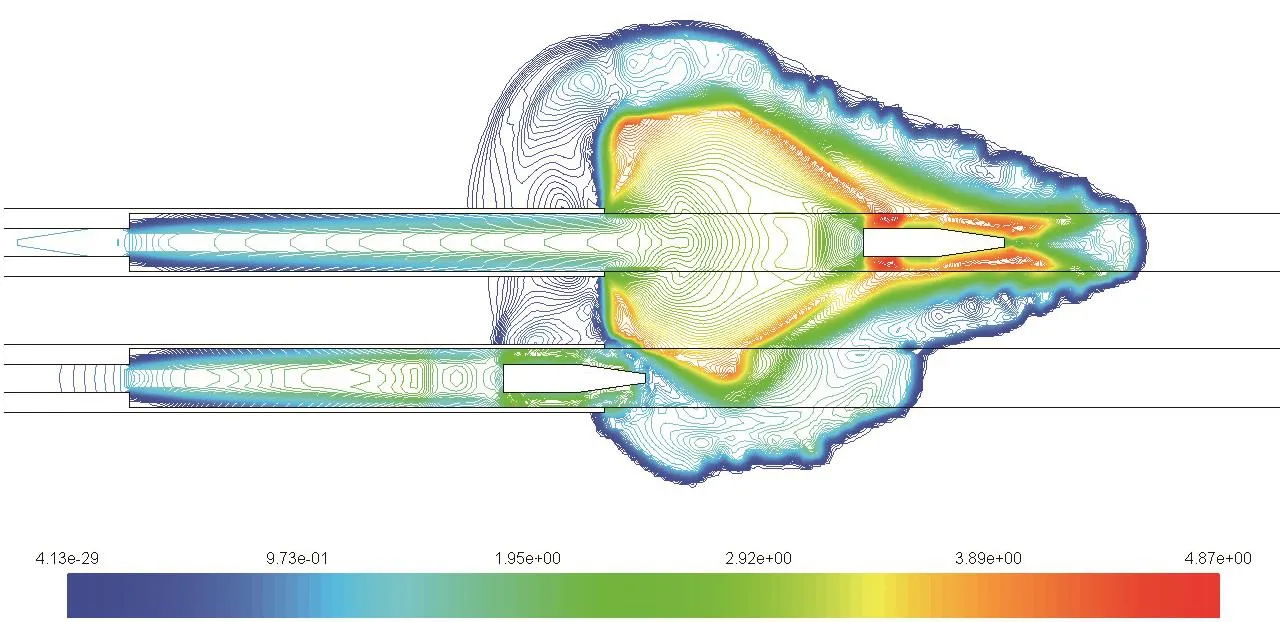
圖9 馬赫數分布圖

圖10至圖13所示為帶300 mm測速裝置的雙身管間隔射擊時,在不同身管間距條件下,彈丸穿越膛口流場過程中的徑向速度與軸向速度的變化情況。

圖10 不同身管間距間隔0.3 ms發射時,彈丸穿越膛口流場的軸向速度變化情況

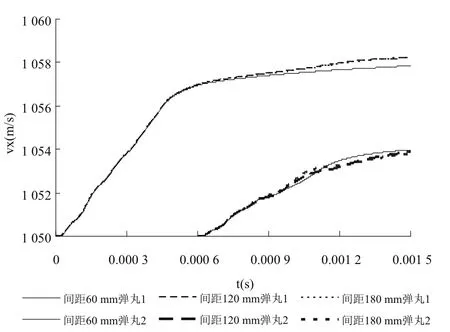
圖12 不同身管間距間隔0.6 ms發射時,彈丸穿越膛口流場的軸向速度變化情況

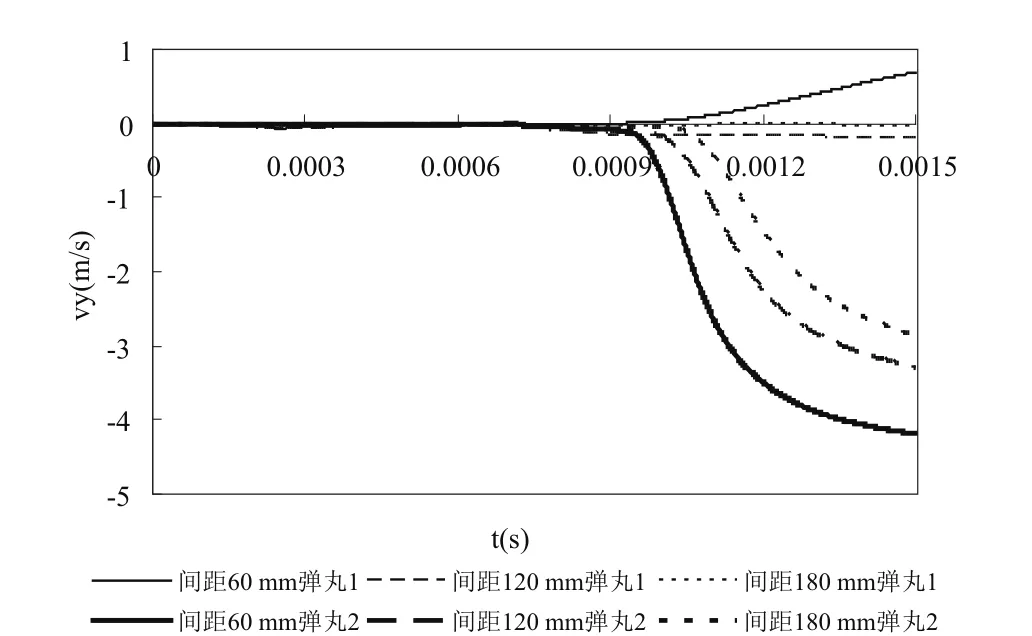
圖１３ 不同身管間距間隔０.６ ｍｓ 發射時?彈丸穿越膛口流場的徑向速度變化情況

由以上分析可以看出:帶測速裝置的雙身管間隔一定時間發射彈丸時,身管間距在一定范圍,膛口流場具有類似的發展規律。當彈丸2進入膛口流場后,與其產生耦合作用。流場結構相似,彈丸附近靜壓梯度較大,受載情況復雜。特別因負壓甚至空腔的存在,將使彈丸受較大俯仰力矩的作用。可以得到以下結論:隨著身管間距的增大,彈丸1的受膛口流場的徑向擾動漸弱,增速均較小,軸向速度則比較相近,呈現減小的趨勢;彈丸2的徑向運動均趨向于與彈丸 1分離,且增速幅值相對較大;當間隔0.3 ms發射時,彈丸2的徑向速度隨雙身管間距呈現出先減小后增大的特點,而當間隔0.6 ms發射時,彈丸2的徑向速度隨雙身管間距增大而減小。

4 結語

后繼發射炮彈受膛口流場的影響與其進入膛口流場的時機和切入位置有重大關聯。分析結果證明了通過控制射速和改變身管間距來降低膛口流場對彈丸運動狀態影響的可行性。

[1]董志勇.射流力學[M].北京:科學出版社,2005.

[2]徐明友.彈箭飛行動力學[M].北京:國防工業出版社,2003.

[3]尤國釗,許厚謙,楊啟仁.中間彈道學[M].北京:國防工業出版社,2003.

[4]江坤.炮口制退器優化設計理論與方法研究[D].南京:南京理工大學博士學位論文,2007.