基于隨機海浪理論的海上浮動平臺運動分析

肖飛

(南京理工大學機械工程學院,江蘇南京210094)

0 引言

海洋探測設備安裝于海上浮動平臺上,平臺臺面為探測基準面,設備運行過程中該基準面應保持水平。由于受到海上風浪等環境的影響,平臺會產生旋轉和晃動[1]。為確保探測設備正常工作,需要對載體擾動進行隔離,因此提出海上浮動平臺實時穩定技術的研究需求。實現海上平臺的實時穩定,首先需要對浮動平臺在隨機海浪下的運動特征有充分的認識。

分析海上浮動平臺在隨機海浪下運動問題時,可以借鑒船舶運動的分析方法[2－4]。但是,一般浮動平臺的結構與普通船舶的結構仍然存在一定的差別。因此,需要針對海上浮動平臺的具體特征,分析其運動特點。

針對海上浮動平臺在隨機海浪下的運動問題,建立了四級海況下的隨機海浪模型,分析了基于該模型的海上浮動平臺的橫搖運動。通過仿真,得到了四級海況下海浪的波高數據和海上浮動平臺在對應海況下的橫搖運動數據。

1 隨機海浪模型

海浪主要包含風浪和涌浪,本文討論的是風浪。風浪是指由當地風產生,并一直處在風作用下的波浪[5]。由于風的大小和方向都是隨機的,因此也就決定了海面上的波浪結構的復雜性。

為簡化問題,在工程應用中,一般假設海浪是二因次的,即假設只在一個平面內產生波浪,且波浪只沿一個固定的方向前進,每個垂直于波浪前進方向的波線是無限長的。因此,經常把僅存在于主風向方向而且有無窮長波線、單向的、波峰彼此保持平行的二因次不規則波浪稱為長峰波浪[6]。

從統計學上來看,二因次不規則海浪可以看作是一個平穩隨機過程,其各項統計值基本保持不變。因此,可以運用平穩隨機過程的分析工具來分析二因次不規則海浪。

隨機海浪模型建立的過程:首先確定海浪頻譜S(ω)以及相應海況下的參數(風速,有效浪高等),然后根據建模的頻率范圍、頻率等分間隔進行離散化處理,這樣就可以根據海浪頻譜,確定不同頻率下的幅值,最后將不同頻率下的幅值疊加起來就得到了隨機海浪模型。

由于二因次隨機海浪可以看作是無數不同波幅和波長的規則波的迭加,則某時刻t,x0處的波高可表示為:

式中,ai為振幅,ki為波數,ωi為角頻率,εi為初相角。 式(1)中海浪頻譜的分布為0~∞,但由海浪理論可知,其主要能量是集中在某一頻段內的,因而可以選取能量集中的頻段中的有限諧波進行仿真,得到的結果也是可以滿足工程運用中的精度要求的。為了簡化問題,取位置x0＝0,式(1)改寫為:

相應的波傾角為:

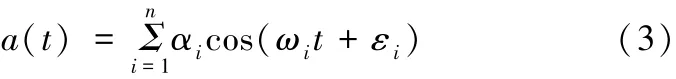
對海浪進行仿真時,通常采用能量譜來進行描述,一般用S(ω)表示。P－M頻譜模型是工程中運用較為廣泛的模型,其表達式為:

式中,p＝5 ,q＝4 ,A＝0.78 ,B＝3.11＝68.54,U 為海面上10 m處的風速,H21/3為有效波高。

離散化的方法有兩種,1)頻率等分發,2)能量等分發,本文選擇了1)方法。本文中討論的是海上浮動平臺在四級海況下的運動規律。查閱相關文獻,選取仿真頻段為0.3 rad/s~2.4 rad/s,有效浪高2.8 m[8]。仿真過程中,選擇頻率等分間隔為0.1 rad/s,得到仿真模型如下:

2 海上浮動平臺運動分析

海上浮動平臺在隨機海浪下的運動可以用6個自由度來描述:沿三個軸的平動和繞三個軸的轉動(如圖1所示)。對海上浮動平臺的姿態產生,主要影響的運動是繞x軸和z軸的轉動,分別稱之為橫搖和縱搖,以及沿y軸的平動,即上下浮動。本文中以橫搖運動為例,分析海上浮動平臺的運動狀況,其余兩種運動的分析方法類似。

海上浮動平臺在隨機海浪作用下的運動,可以看作一個能量轉換系統,波高ξ＝(t)為系統輸入,而橫搖運動θ(t)可以看作是系統的輸出。

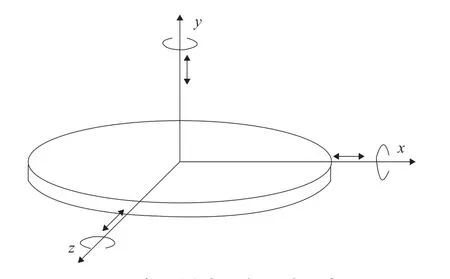
圖1 海上浮動平臺運動示意圖

即海上浮動平臺在隨機海浪下的運動是一個二階振蕩環節。

對于該系統,可以參照船舶的橫搖運動傳遞函數[8]:

3 結果分析與討論

為了進一步驗證模型的合理性,以了解海上浮動平臺的運動規律,運用Matlab軟件對隨機海浪以及海上浮動平臺的橫搖運動進行仿真分析。

海上浮動平臺的主要參數如表1所示。

表1 系統參數

圖2是四級海況條件下波高變化圖。圖3是對應圖2隨機海浪條件下海上浮動平臺的橫搖角。

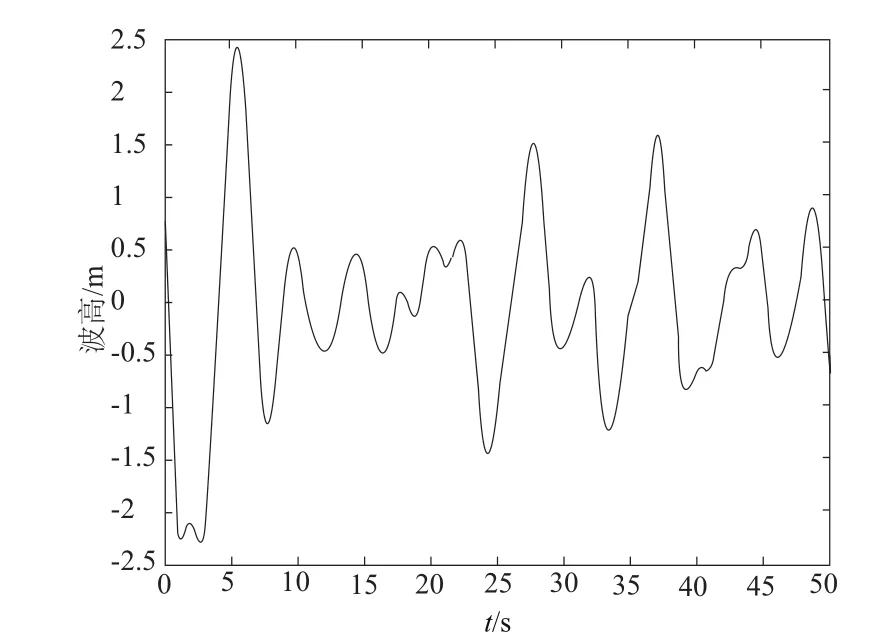
圖2 四級海況下的波高圖

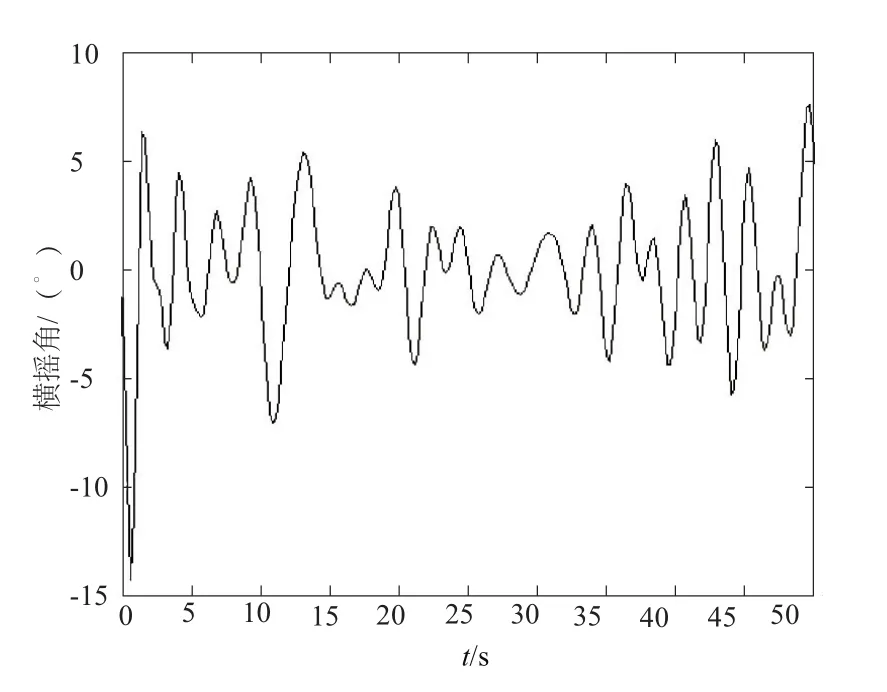
圖3 四級海況下平臺橫搖運動

根據仿真結果可知,浪高約為1 m~2.5 m。通過查詢海況表,四級海況的浪高范圍是1.25 m~2.5 m。因此,可以看出,海浪的仿真結果滿足四級海浪的波高特性。同時,基于該隨機海浪模型得到的海上浮動平臺橫搖運動特性后續研究參考。

4 結語

針對海上浮動平臺在隨機海浪下的運動問題,建立了四級海況下的隨機海浪模型,分析了基于該模型的海上浮動平臺的橫搖運動。通過仿真,得到了四級海況下海浪的波高數據和海上浮動平臺在對應海況下的橫搖運動數據。結果表明:該方法可以有效地模擬隨機海浪以及分析海上浮動平臺的運動,為后續研究打下基礎。

[1]金振逸,馬少杰.基于線性波浪理論的海上浮動平臺受力及運動分析[J].四川兵工學報,2011,8:135-137.

[2]Yan-sheng Y.Review on ship motion control[J].Journal of Traffic and Transportation Engineering, 2003, 3(2):34-39.

[3]Kim Y,Shin Y S,Lin W M,et al.Study on sloshing problem coupled with ship motion in waves[C]//Proceedings of the 8th International Conference on Numerical Ship Hydrodynamics,Busan,Korea.2003.

[4]李殿璞.船舶運動與建模[M].北京:國防工業出版社,2008.

[5]李水清,趙棟梁.風浪和涌浪分離方法的比較[J].海洋學報, 2011, 33(6):1-7.

[6]金鴻章.長峰波隨機海浪的實時仿真和頻譜分析[J].船舶工程, 1987(1):24-32.

[7]郭惜久,程翔.隨機海浪模型仿真[J].四川兵工學報,2010,31(008):134-136.

[8]范海平.基于卡爾曼濾波技術的船舶橫搖預測方法研究[D].哈爾濱:哈爾濱工程大學,2008.