關于瓷套變形問題的探討
焦國鋒,李風芹,范建二,顧瑞云
(1.南京電氣集團有限責任公司,江蘇南京210038;2.南京工業職業技術學院,江蘇南京210046)
0 引言

圖1 電容瓷套
大瓷套的變形是瓷套生產過程中一個常見的產品缺陷。變形有多種形式,如瓷套的孔口橢圓變形、瓷套的軸向彎曲變形等,本文主要針對瓷套軸向彎曲變形進行討論。
瓷套的彎曲變形與料方的性能以及工藝過程控制等都有密切的關系,但在生產中曾經發現這樣一個現象:電容瓷套(b)和電容瓷套(a)在幾何尺寸方面是非常相近的兩個產品(圖1),但是從數次檢測的結果看,003621-9.2產品變形相對較多、較大。比較兩個產品發現,兩個產品的傘伸出、下內孔以及壁厚均接近,較大的區別是003621-6.2圖1(a)直體部分比003621-9.2短,重心低47 mm,質量少21 kg。長期的生產經驗認為,當產品的質量越重(質量越大),產品高度高,重心高,產品變形傾向越大。因此選擇瓷套的質量(m)、瓷套重心距離瓷套下端面高度h與自身總高度H的比(h/H)以及瓷套的穩度(W)對瓷套變形情況加以統計分析。
1 對統計量的說明以及進一步選擇
2.1 穩度(W)
穩度是把物體翻倒的難易程度,物體穩度大小一般用翻倒它時所做功來描述。圖2所示AO是瓷套重心O所在鉛垂線,AB是瓷套底面半徑,BC∥AO,且BC=AO。當瓷套重心O沿圓弧OD移動到D后,則瓷套自動傾倒。在這個過程中O升高距離CD,所做的功可用下式表示:
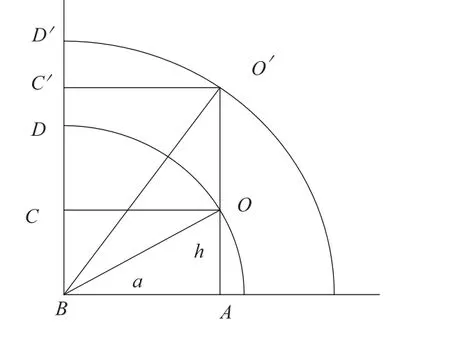
圖2 穩度示意圖

知穩度是a的增函數,a變大時W變大。
物體G不變,當重心O提高到O′,由圖2可明顯看出即重心提高使物體穩度降低。
1.2 關于瓷套重心Z和重心高度h
因為所研究的瓷套體積不太大,可認為瓷套處于均勻的重力場中(即瓷套體積內各處的重力加速度g大小相等,方向平行),瓷套重心與質心的位置是重合的。通過CAD繪圖可求得瓷套質心,即瓷套重心,同時也可求得重心距瓷套底面的高度h,從而可以進一步計算h與H(瓷套自身高度)的比。
1.3 瓷套的質量(m)與(h/H)以及統計量的選擇
經驗認為,瓷套質量m越大,瓷套所受的重力越大,由于瓷套高溫荷重能力的限制,因此更容易產生變形。
從穩度的計算式(1)看,物體質量m與穩度W是相關的,因為公式中G=mg。為了選擇相對獨立的統計量,根據相關系數計算公式:
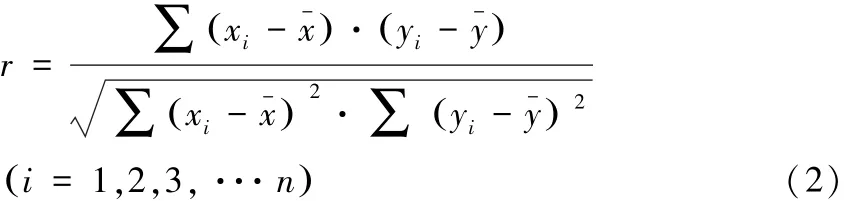
式中:xi,yi——所選統計量的觀測值;
利用表1中的數據,計算所選統計量間的相關系數如表2。

表1 相對變形較大、易產生變形的瓷套類
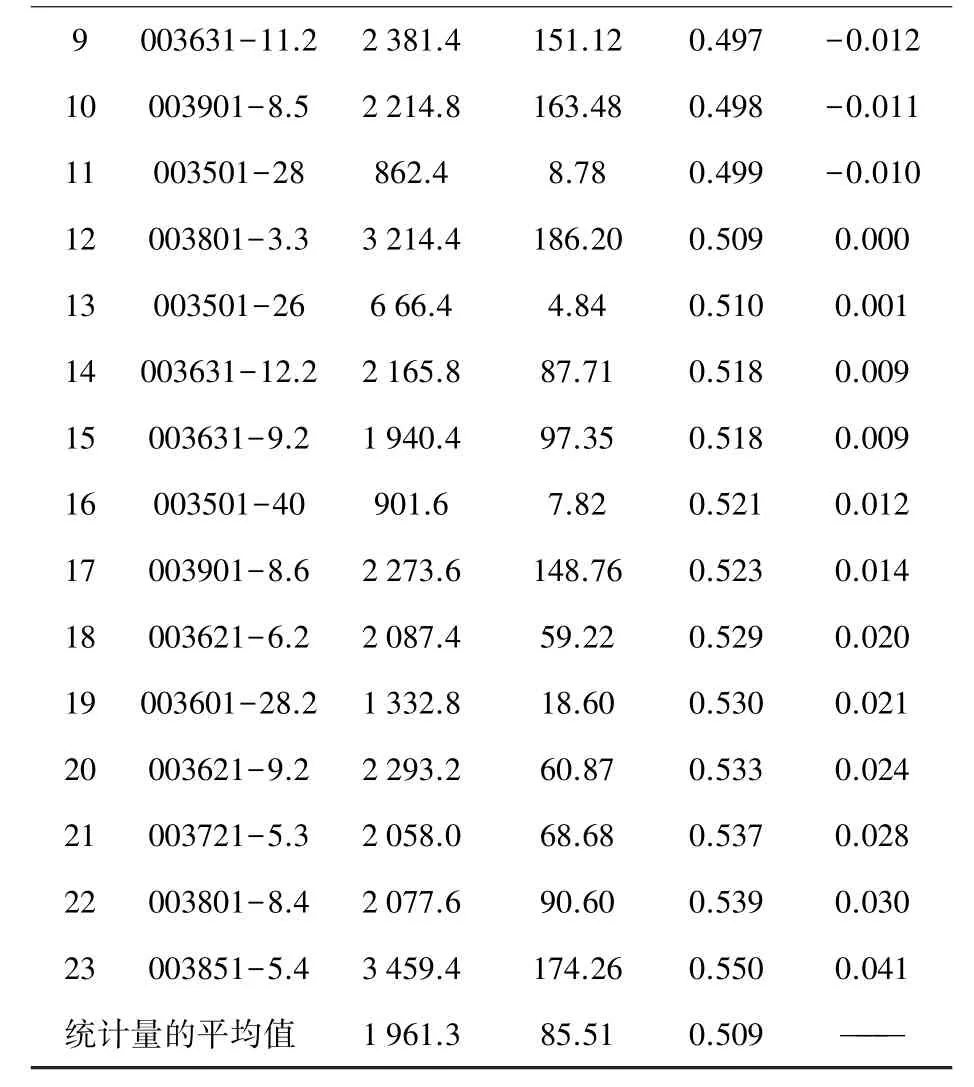
續表1

表2 各統計量間的相關性
通過表2中數據可看出,瓷套質量m與瓷套穩度W有較強的相關性(相關系數是0.912)。因此可取其一作為統計量,另外瓷套質量m與h/H(瓷套重心距離瓷套下端面高度與瓷套總高度之比)的相關系數是0.167,瓷套穩度W與h/H的相關系數是0.013,因此選擇W與h/H作為統計量。
2 抽樣分析
2.1 排序分析
抽取樣本如表3所示。針對統計量(W與h/H)分別排序分析,按穩度W列排序,未發現規律;但是h/H列按升序排列后,規律性較強,與生產實際相對照:17行之前各產品相對變形小或不變形;17行之后各產品相對變形較大或易產生變形。因此將表3中數據分為兩類列于表1和表4中。

表3 樣本按重心高度h與瓷套高度H之比(h/H)排序
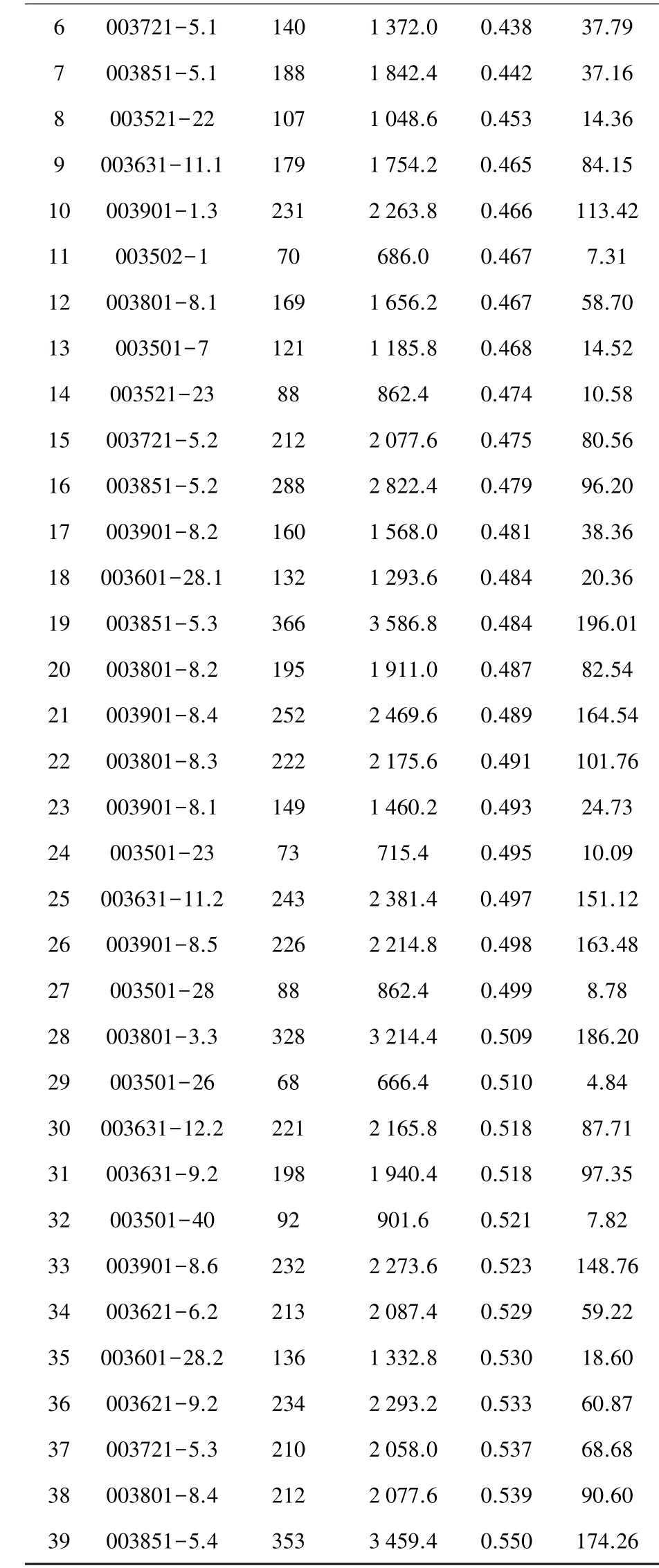
續表3
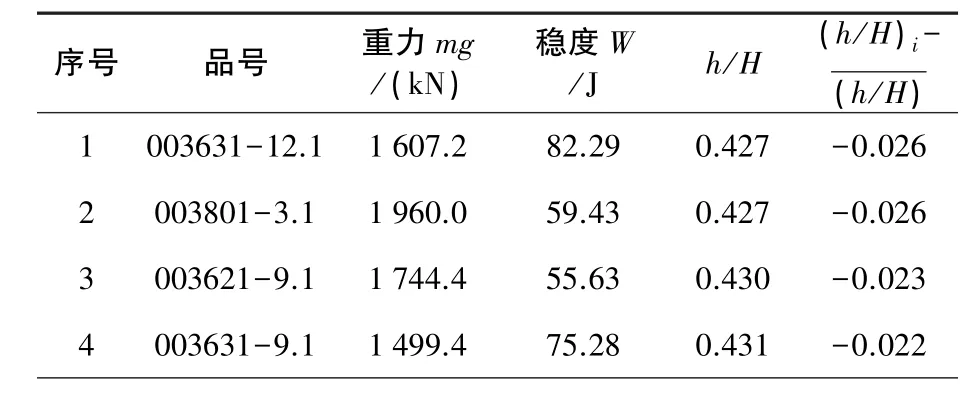
表4 相對變形小或不變形的瓷套類
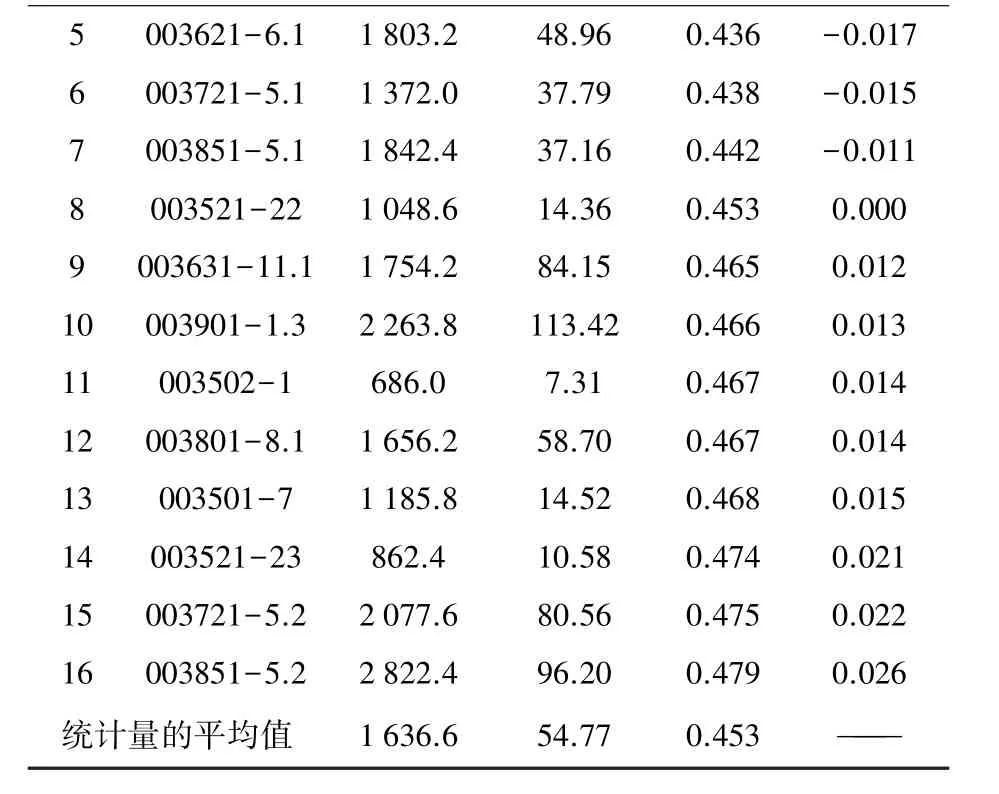
續表4_
通過排序發現用穩度W大小來描述產品變形情況,與生產實際的符合性不好,因為有些產品的穩度值很小,很接近,但卻是兩種相反的情況。
如表5所示003501-23和003521-23的穩度值很接近,而003502-1產品的穩度值甚至小于003501-23,但是003521-23、003502-1由于是帶錐度的塔形產品,所以變形很少(表5中所列帶錐度的塔形產品均變形很少),而003501-23由于是直筒形的產品,所以變形較多。因此產品的幾何形狀對產品的變形有較大影響。
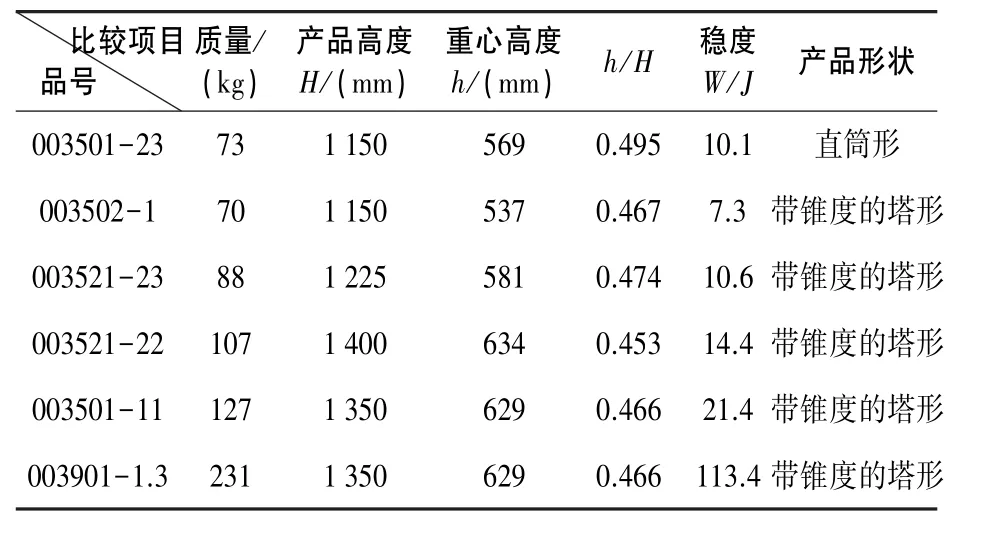
表5 穩度W與h/H統計量的比較
穩度的計算關系到了產品的幾何形狀,但是用瓷套重心高度與產品自身高度的比來描述瓷套的穩度更確切,因為重心是由瓷套的幾何形狀和瓷的質量分布均勻性確定的,瓷的質量分布可以認為是均一的(即瓷的體積密度是均一的),所以瓷套的重心與瓷套的幾何形狀密切相關,另外瓷套均近似為圓筒形,可抽象為“直桿”,一根頭重腳輕的桿更容易傾倒,是一個簡單的物理現象,而h/H描述了“桿”“頭重”的程度,因此用h/H描述瓷套的穩度更確切,以下分析主要針對h/H統計量進行分析。
由表5還可以看出,瓷套的質量和自身高度對瓷套的變形不是決定性的。如003501-11和003521-22兩個產品的自身高度和質量都大于003501-23產品的高度和質量,而它們的變形很少(表中003901-1.3產品的情況更能說明該問題)。因此經驗認為瓷套的質量大、高度高,就產生變形,是一種不準確的認識。
2.2 對兩類產品總體參數推斷分析
1)相對變形小或不變形類瓷套(h/H)總體均值的區間估計
選擇顯著性水平a=0.05,計算(h/H)總體均值95%的置信區間。a/2=0.025,由表2知 n=16。
因為總體方差σ2未知,因此選擇隨機變量

通過以上計算知:相對變形小或不變形類產品(h/H)總體均值u的95%置信區間是[0.443,0.463]。
2)相對變形較大、易產生變形的瓷套類(h/H)總體均值的區間估計
選擇顯著性水平a=0.05,根據表1數據對該類瓷套(h/H)總體均值進行區間估計,計算步驟同1),計算結果如表6。

表6 相對變形較大、易產生變形的瓷套類(h/H)總體均值的區間估計
3 結語
1)經驗認為瓷套的質量大、高度高,會產生變形,是一種不準確的認識。
2)瓷套的幾何形狀對變形有較大的影響,采用統計量h/H能較好地判別瓷套的變形。通過對相對變形小或不變形類瓷套(h/H)總體均值的區間估計,和相對變形較大、易產生變形的瓷套類(h/H)總體均值的區間估計,認為只要瓷套的(h/H)接近或超過0.500,即會產生彎曲變形的傾向。
3)對于公司現在使用的產品配方和現有的產品,通過以上計算知:相對變形小或不變形類瓷套(h/H)總體均值u的95%置信區間是[0.443,0.463];相對變形較大或易產生變形類瓷套(h/H)總體均值u的95%置信區間是[0.500,0.518]。
[1]全國質量專業技術人員職業資格考試辦公室組織編寫.質量專業理論與實務[M].北京:中國人事出版社,2007.1.
[2]何燦芝,吳俊杰.概率論與數理統計[M].湖南:科學技術出版社,1994.
[3]王式安.數理統計方法及應用模型[M].北京:北京科學技術出版社,1992.11.
[4]李濟群.AUTO CAD機械制圖基礎教程[M].北京:清華大學出版社,2011.5.

