以入射角定權的點云數據加權總體最小二乘平面擬合研究*

蒼桂華 李明峰 岳建平

1)南京工業(yè)大學測繪學院，南京 210009

2)河海大學地球科學與工程學院，南京 210098

以入射角定權的點云數據加權總體最小二乘平面擬合研究*

蒼桂華1)李明峰1)岳建平2)

1)南京工業(yè)大學測繪學院，南京 210009

2)河海大學地球科學與工程學院，南京 210098

顧及入射角對點云數據點位精度的影響，提出入射角定權的點云數據加權總體最小二乘平面擬合方法。該方法以加權總體最小二乘方法為基礎，利用入射角信息確定點云數據中各點的平面擬合權重，并根據系數矩陣結構特點定義其權陣。通過3種不同材質平面樣本數據的計算分析表明，與最小二乘法、總體最小二乘法相比，該方法可得到更高的平面擬合精度。

點云數據;平面擬合;加權總體最小二乘;入射角定權;系數矩陣

地面三維激光現實掃描場景中含有大量平面特征，可用于前期數據預處理或后期建模的數據簡化，還可用于多視點云數據配準，實現建模。平面特征的提取是利用點云數據進行3D建模的一項重要工作，提取精度直接關系到后續(xù)應用成果的精度。以往提取平面特征常用的方法為最小二乘平面擬合法。此方法根據點的三維坐標(xi，yi，zi)建立平面方程z=ax+by+c，假設誤差e只存在于觀測向量Z 中，建立高斯-馬爾科夫(Gauss-Markov，G-M)模型，采用最小二乘(least squares，LS)方法擬合平面，獲取平面擬合參數。然而，由于儀器設備、外界環(huán)境、地物特性等因素影響，使得實際點云數據的xi、yi、zi三個觀測值中均存在誤差，從而使包含變量xi、yi的系數矩陣A也含有誤差。因此，利用最小二乘法進行平面數據擬合的結果不是最優(yōu)，而是有偏的［1］。針對這種觀測向量和系數矩陣均包含誤差的模型，即所謂的變量中的誤差(error-in-variables，EIV)模型，Golub等［2］最早提出了總體最小二乘(total least squares，TLS)估計方法。但總體最小二乘估計僅在設計矩陣和殘差元素均服從獨立等精度分布時才是最優(yōu)估計［3］，而實際點云數據各點的精度是不等的，因此簡單的總體最小二乘方法并非最優(yōu)估計［4］。為了解決矩陣和殘差的不等精度估計問題，Markovsky等［5］提出了加權總體最小二乘(weighted total least squares，WTLS)方法。Schaffrin等［6］則進一步擴展了WTLS方法。國內學者也從理論、應用等方面對 WTLS方法進行了深入研究［7－10］。本文根據入射角對點云數據點位精度的影響，提出利用入射角定權的加權總體最小二乘點云數據平面擬合方法，簡稱角度加權總體最小二乘(angle weighted total least squares，AWTLS)方法。

1 LS、TLS、WTLS 三種方法及其平差模型

點云數據經過粗差剔除預處理后得到一組平面點云的三維坐標(xi，yi，zi)(i=1，2，…，n)。設空間平面方程式為:

式中，a、b、c為待求的平面擬合參數。將式(1)寫成矩陣形式為:

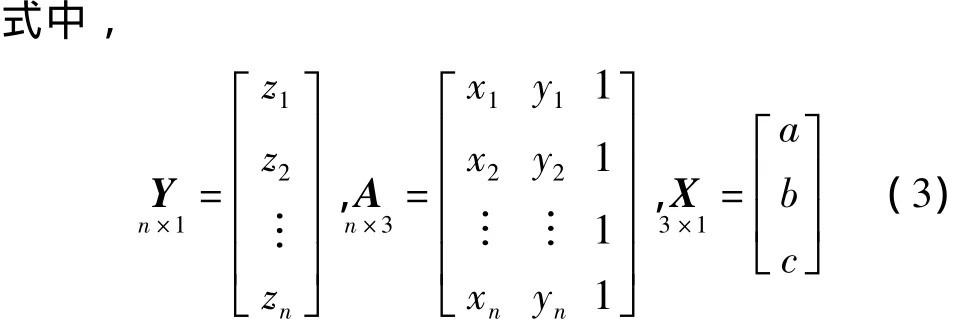
若同時考慮觀測向量Y和系數矩陣A的誤差，則建立EIV函數模型［6］:

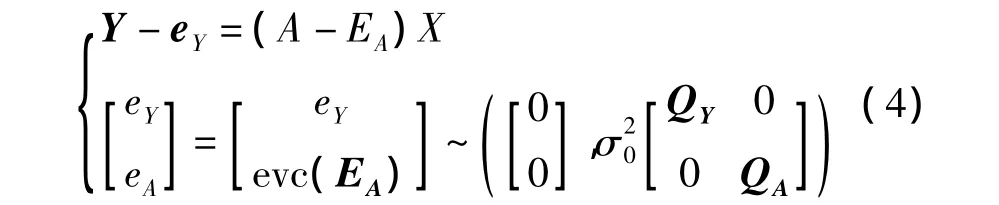
式中，eY和EA分別表示觀測向量Y和系數矩陣A的隨機誤差矩陣;vec是指將矩陣按列拉直所得到的列向量，排列順序為從左到右;eA=vec(EA)∈R3n×1表示矩陣EA按列向量化后得到的向量;σ20為未知的單位權方差;QY=P－1Y，QA=P－1A，分別表示觀測向量和系數陣列向量化向量的協(xié)因素陣。

根據eA及其相關權陣的設置，采用不同的估計方法進行平面擬合參數的求解。

1)eA≡0。此時只考慮觀測向量Y的誤差，則EIV模型變?yōu)榻浀錅y量平差的G-M模型:

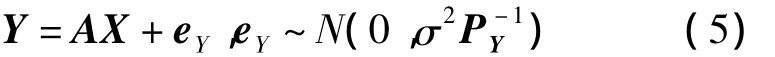
應采用最小二乘法進行參數估計。

2)eA≠0，但 QY=In，QA=Inm。此時假設點云數據坐標獨立且等精度，即觀測向量權陣PY和系數矩陣權陣PA均為單位陣，采用總體最小二乘法進行參數估算。

3)eA≠0，QY、QA均不為單位陣。此時，假設點云數據坐標為不等精度，采用加權總體最小二乘法進行參數估計。根據系數矩陣的結構特點設計權陣P0、Px、PY。P0是3×3矩陣，代表系數矩陣 A 的列向量權陣;PX是n×n矩陣，代表系數矩陣A的行向量權陣;PY是n×n矩陣，代表矩陣Y的權陣。P0、PX、PY相應的協(xié)因素矩陣為 Q0、QX、QY，即

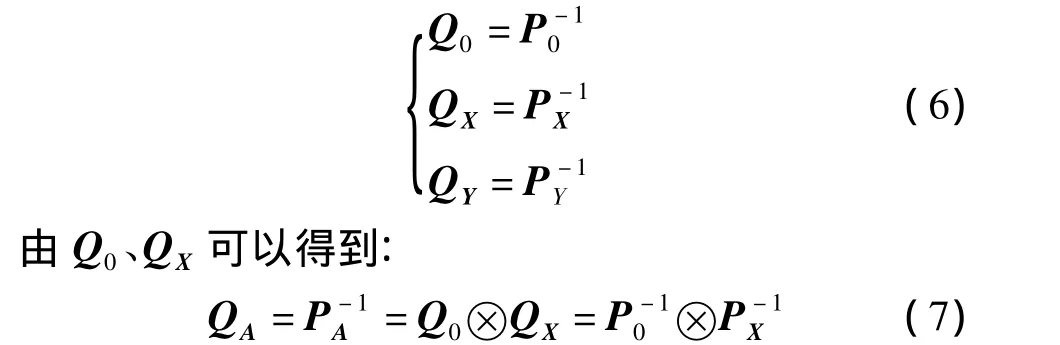
式中，?表示“kronecker積”。

3 種估算方法的估計準則和單位權方差估計如表1所示。

表1 3種方法的估算準則和單位權方差估計Tab.1 Estimation criterions and unit weight estimation variances with three methods

2 AWTLS方法權陣的確定及其步驟

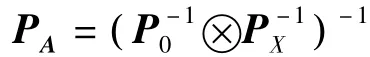
2.1 權陣的確定

點云數據中各點的精度不等，進行平面擬合時應根據各點精度確定其擬合權重。點位精度越高，參與擬合的權重也越大，從而保證結果的精度。相關文獻研究了入射角對點云數據精度的影響，指出點云數據入射角越小則點位精度越高［11－12］。而入射角越小，其余弦值越大，因此可將各點入射角余弦值作為其擬合權重。平面點云數據的各點入射角θ定義為入射光線與平面法向量之間的夾角［13］。設擬合的平面方程如式(1)所示，則平面上i點的入射角余弦值或其擬合權值為:

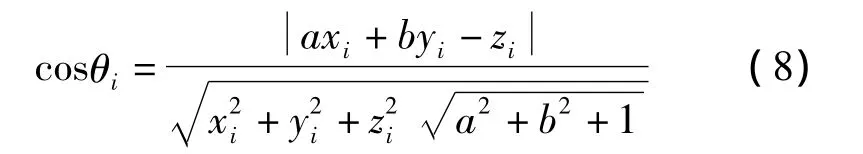
式中，θi為 i點的入射角，(xi，yi，zi)為點 i的三維坐標，(a，b，－1)為擬合平面的法向量。

設點云在x、y、z三個方向等精度獲取，對于平面的系數陣列向量和觀測向量，有σx=σy=σz。結合系數矩陣A的特點，設置相應權陣:

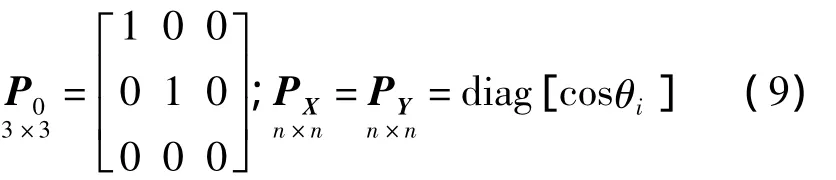
式中，P0的第三個對角元素為0，表示系數矩陣A中第三列不需要改正;其余對角線元素為1，表示系數矩陣A中的第一、二列中的元素是等精度獲取的;PX、PY與入射角有關。

2.2 方法步驟

由式(9)可以看出，權陣PX、PY與平面擬合參數相關，因此需要迭代求解。AWTLS方法的具體步驟如下:

1)將最小二乘平面擬合參數作為起始解，根據式(8)計算各點的入射角余弦值，組成相關矩陣P0、PX、PY。

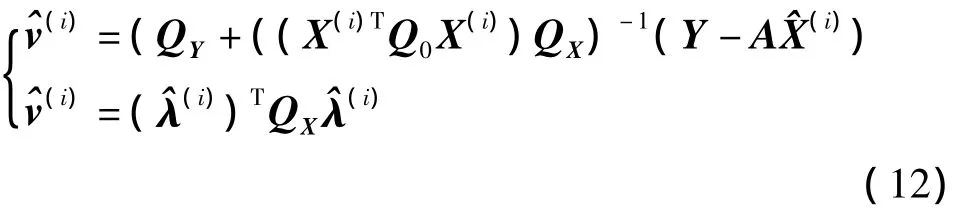
5)重新計算每點的入射角余弦值，設置相關權陣 P0、PX、PY，計算(i+1):

3 算例分析

為驗證AWTLS方法的可行性，采用3種不同材質的平面點云樣本數據進行實驗。實驗的平面樣本有標準反射板(反射率為35%)、普通木板及一般的水泥建材模板。3種材質樣本中，標準反射板均質性最好，板面最平整;普通木板均質性和平面度次之;建材水泥模板均質性和平面度最差，但其平面偏差目測在1 mm以內。利用徠卡HDS ScanStation2分別對樣本進行掃描，獲取平面點云數據(圖1)。

根據點云數據特點確定平面形式［14］。分別利用最小二乘法、總體最小二乘法和AWTLS法對各樣本點云數據進行平面擬合，獲得平面擬合參數、、以及單位權中誤差(0)。假設確定的平面形式如式(1)所示，由式(15)計算點云數據各點到擬合面的距離(di)以及平面擬合精度(P)，并得到點到擬合面的最大距離(max(di)):

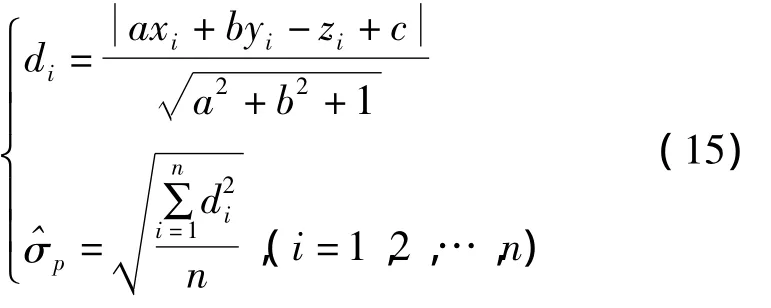
式中，n為擬合平面上點的個數。

將單位權中誤差、點到擬合面的最大距離、平面擬合精度作為估算方法優(yōu)劣的評判指標。用3種方法對3種材質的樣本數據進行平面擬合，結果如表2所示。

從表2可以看出，不論何種材質樣本，LS方法的單位權中誤差都遠遠大于TLS方法和AWTLS方法，而TLS和AWTLS方法的單位權中誤差為同一數量級，這是因為LS方法與TLS方法以及AWTLS方法的單位權中誤差計算方法不同所致。另外，對于3種材質的樣本數據，利用AWTLS方法獲得的3個精度判定指標均要比LS方法和TLS方法小得多。以平面度和均質性最差的水泥模板為例，利用AWTLS方法得到的單位權中誤差比TLS方法提高了65%，平面擬合精度比LS方法和TLS方法分別提高了63%和19%，點到擬合面的最大距離也由LS方法和TLS方法的9.1 mm和7.0 mm 降為5.3 mm。

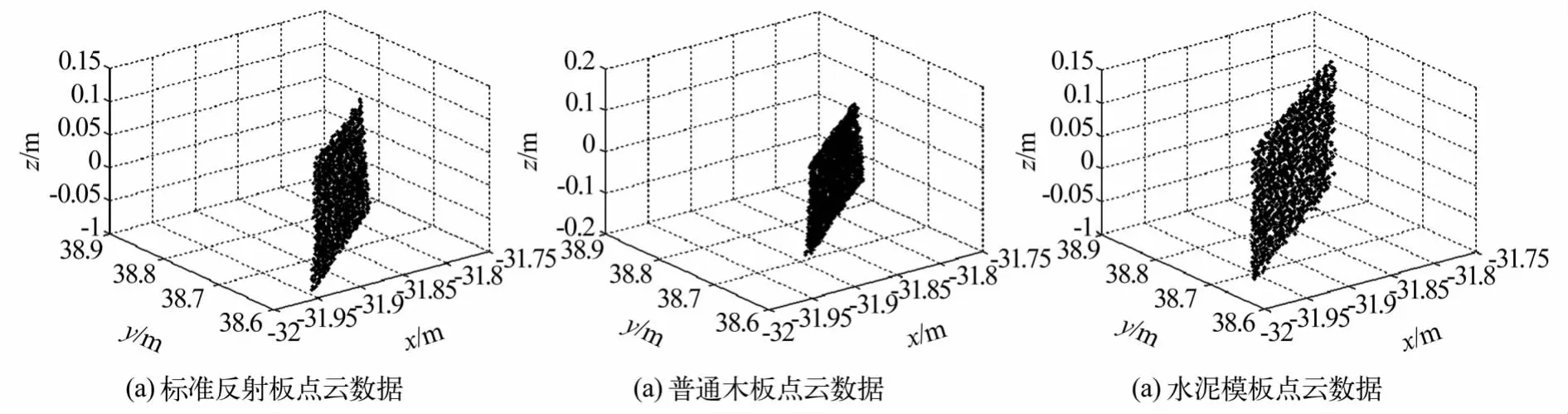
圖1 實驗樣本的平面點云數據Fig.1 Plane point clouds used in the experiments

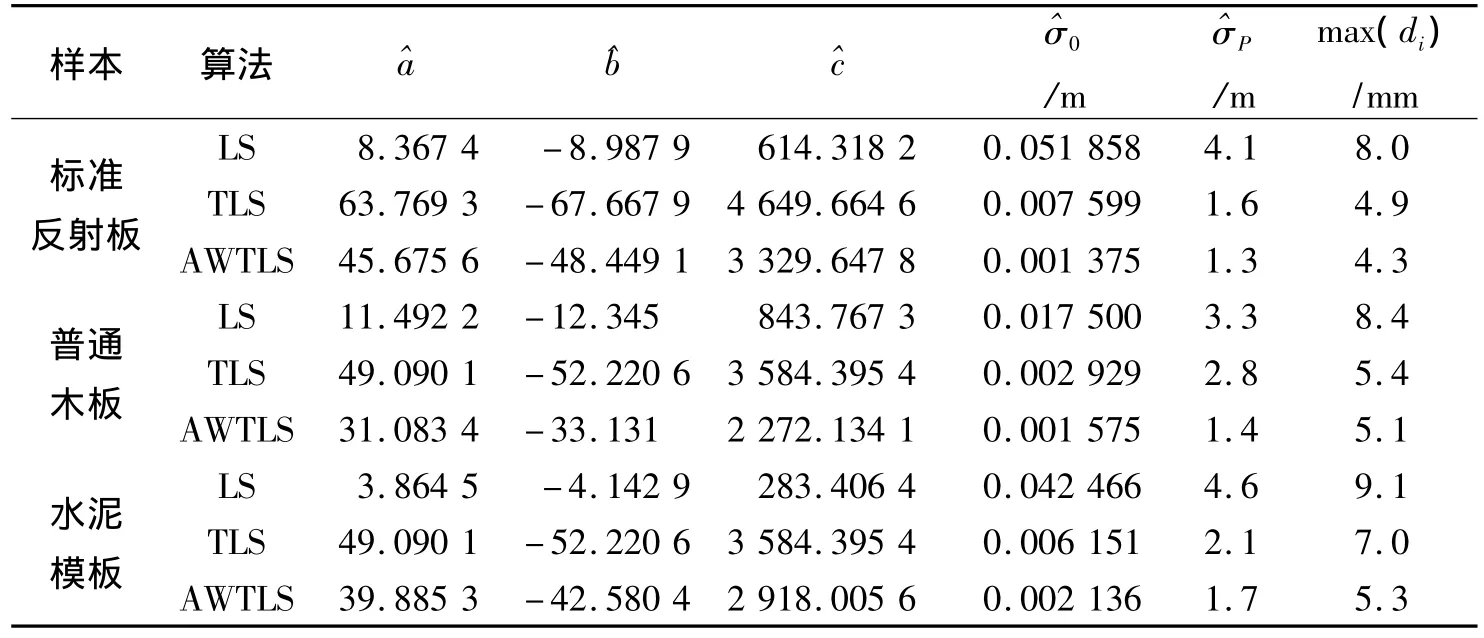
表2 三種方法下平面點云數據擬合的相關計算結果Tab.2 Fitting results of plane samples

4 結論

1)AWTLS方法是在加權總體最小二乘方法基礎上，利用入射角對點云數據精度的影響確定各點的擬合權重。從實驗結果看，該定權方法符合點云數據平面擬合的實際，結果也更加合理。

2)由于LS方法、TLS方法以及AWTLS方法的單位權中誤差計算方法不同，因此不能簡單地以單位權中誤差的大小來判定某個估算方法的優(yōu)劣，應結合其他精度評判指標進行評定。

3)AWTLS方法系數矩陣的行向量權陣PX和觀測向量權矩陣PY與擬合參數有關，因此在計算過程中需要迭代運算。

利用WTLS方法進行點云數據平面擬合的關鍵是如何確定各點的擬合權值。本文只進行了利用入射角定權的WTLS方法在點云數據平面擬合中的適用性研究，后續(xù)將進一步研究其他權值確定方法，并與本文的AWTLS方法進行比較，研究各方法的優(yōu)劣。

1 邱衛(wèi)寧，等.測量數據處理理論與方法［M］.武漢:武漢大學出版社，2008.(Qiu Weining，et al.The theory and method of surveying data processing［M］.Wuhan:Wuhan University Press，2008)

2 Golub H G，Loan C F.An analysis of the total least squares problem［J］.SIAM Journal on Numerical Analysis，1980，17(6):883－893.

3 Van H S，Vandewalle J.The total least squares problem:computational aspects and analysis［M］.Philadelphia:SIAM，1991.

4 周擁軍，鄧才華.加權和不加權TLS方法及其在不等精度坐標變換中的應用［J］.武漢大學學報:信息科學版，2012，37(8):976 － 979.(Zhou Yongjun，Deng Caihua.Weighted and unweighted total least square methods and applications to heteroscedastic 3d coordinate transformation［J］.Geomatics and Information Science of Wuhan University，2012，37(8):976 －979)

5 Markovsky I，et al.The element-wise weighted total leastsquares problem ［J］.Computational Statistics and Data A-nalysis，2006，50:181 －209.

6 Schaffrin B，Wieser A.On weighted total least-square adjustment for linear regression［J］.Journal of Geodesy，2008，82(7):415－421.

7 王樂洋，許才軍，魯鐵定.病態(tài)加權總體最小二乘平差的嶺估計解法［J］.武漢大學學報:信息科學版，2010，35(11):1 346 － 1 350.(Wang Leyang，Xu Caijun，Lu Tieding.Ridge estimation method in ill-posed weighted total least squares adjustment［J］.Geomatics and Information Science of Wuhan University，2010，35(11):1 346 －1 350)

8 趙輝.基于加權總體最小二乘的GPS數據高程擬合［J］.大地測量與地球動力學，2011，31(5):88 －90，96.(Zhao Hui.GPS height fitting of weighted total least-squares adjustment［J］.Journal of Geodesy and Geodynamics，2011，31(5):88 －90，96)

9 周擁軍，朱建軍，鄧才華.附參數的條件平差與按行獨立的加權總體最小二乘法估計的一致性研究［J］.測繪學報，2012，41(1):48 － 53.(Zhou Yongjun，Zhu Jianjun，Deng Caihua.The consistency between row-wised weighted total least squares and condition adjustment with parameters［J］.Acta Geodaetica et Cartographica Sinica，2012，41(1):48－53)

10 陳瑋嫻，等.加權總體最小二乘在三維激光標靶擬合中的應用［J］.大地測量學與地球動力學，2010，30(5):90－96.(Chen Weixian，et al.Application of weighted total least squares to target fitting of three-dimensional laser scanning［J］.Journal of Geodesy and Geodynamics，2010，30(5):90－96)

11 Soudarissanane S，Van R J，Bucksch A，et al.Error budget of terrestrial laser scanning:influence of the incidence angle on the scan quality［C］.3D-Nord Ost，Berlin，2007.

12 Soudarissanane S，et al.Incidence angle influence on the quality of terrestrial laser scanning points［C］.ISPRS Workshop Laserscanning，2009.

13 Soudarissanane S，et al.Scanning geometry:influence factor on the quality of terrestrial laser scanning points［J］.ISPRS Journal of Photogrammetry and Remote Sensing，2011，66(4):389－399.

14 王解先，季凱敏.工業(yè)測量擬合［M］.北京:測繪出版社，2008.(Wang Jiexian，Ji Kaimin.Industrial measurement fitting［M］.Beijing:Surveying and Mapping Press，2008)

STUDY ON POINT CLOUDS PLANE FITTING WITH WEIGHTED TOTAL LEAST SQUARES BASED ON INCIDENCE ANGLE WEIGHTING

Cang Guihua1)，Li Mingfeng1)and Yue Jianping2)
1)Department of Geomatics Engineering，Nanjing University of Technology，Nanjing 210009
2)School of Earth Sciences and Engineering，Hohai University，Nanjing210098

The incidence angle has an impact on point clouds accuracyin 3d terrestrial laser scanning.For improving the accuracy，a method of weighted total least squares(WTLS)incidence angle weighting for point clouds plane fitting is proposed.In the method，the weight value of each point is determined by incidence angle，and the weight matrix is defineson the basis of the structure characteristics of coefficient matrix.The experiments with point clouds data of the plane made of three different materials show that the method is more reasonable and more accurate than least squares(LS)and total least squares(TLS).

point clouds;plane fitting;weighted total least squares(WTLS);incidence angle;coefficient matrix

P207

A

1671-5942(2014)03-0095-04

2013-09-22

國家自然科學基金項目(41174002);江蘇省測繪科研項目(JSCHKY201303)。

蒼桂華，女，1971年生，講師，主要研究方向為攝影測量與遙感、大地測量與測繪工程數據處理。E－mail:ghuac@163.com。