基于灰色模型與小波神經網絡的衛星鐘差預報方法*

王宇譜 呂志平 陳正生 黃令勇

(信息工程大學地理空間信息學院，鄭州 450052)

基于灰色模型與小波神經網絡的衛星鐘差預報方法*

王宇譜 呂志平 陳正生 黃令勇

(信息工程大學地理空間信息學院，鄭州 450052)

提出一種基于灰色模型和小波神經網絡相結合的衛星鐘差預報方法。首先通過灰色模型對鐘差進行擬合并確定鐘差預報的灰色模型，然后根據擬合殘差對小波神經網絡進行建模，最后將兩種模型對應的預報結果結合得到鐘差預報值。使用IGS精密鐘差進行實驗，證明該方法的預報效果優于二次多項式模型和灰色模型，特別是對于ⅡR型銣鐘和ⅡF型銣鐘，其預報精度可以提高2倍以上。

衛星鐘差預報;灰色模型;小波神經網絡;慣性制導系統;組合預報模型

衛星導航系統中，鐘差預報的精度直接決定了系統實時導航定位的性能［1］。研究表明，星載原子鐘的頻率總波動由多種不同的噪聲線性疊加而成［2］，這使得建立精確的星載原子鐘運行模型變得困難，也使得鐘差的高精度預報變得困難。為此，建立了多種鐘差預報模型［3－7］，其中最常用的為二次多項式模型和灰色模型(GM(1，1))。文獻［8］將GM(1，1)模型用于鐘差預報，但短期預報效果不佳［9］。本文在文獻［10］的基礎上，建立了一種基于GM(1，1)與小波神經網絡(WNN)相結合的組合鐘差預報方法。該方法既改善了GM(1，1)短期預報的效果，又避免了構造復雜的神經網絡結構，并得到較兩種常用鐘差預報模型更好的預報結果。

1 算法原理

1.1 GM(1，1)模型

設 L(0)={l(0)(i)，i=1，2，…，n}為初始鐘差值序列，l(0)累加一次得:

由最小二乘法，得:

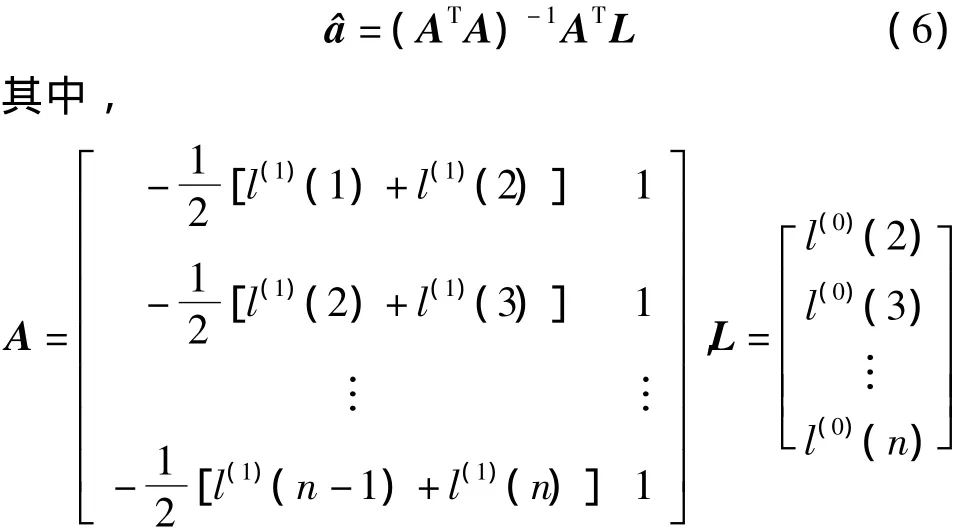
1.2 小波神經網絡［13－14］

假設有L組數據，每組數據由N個分量組成，將其表示為 T=(t(1)，…，t(j)，…，t(L))，t(j)∈RN;模型輸出為一個P維向量，記為O=(o(1)，…，o(j)，…，o(L))，o(j)∈RP。則輸入量經小波神經網絡傳播后輸出為［14］:

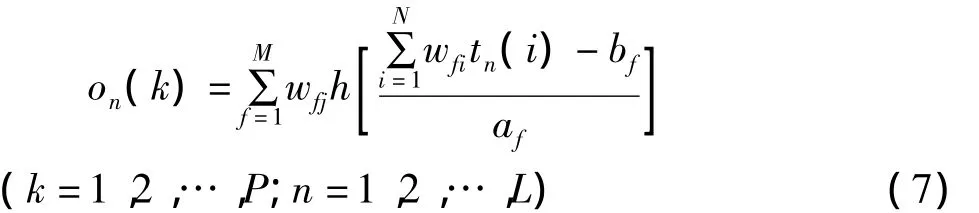
式中，M為網絡隱含層神經元的個數，h(·)為隱含層的小波基函數，tn(i)是輸入數據中第n組數據的第i個分量值，N為每組輸入數據的個數，wfi為連接輸入層節點i和隱含層節點f的權值，wfj為連接隱含層節點f和輸出節點j的權值，af、bf為隱含層節點f的伸縮、平移因子，on(k)為對應的神經網絡輸出值。

1.3 灰色模型與小波神經網絡相結合的組合預報方法

組合預報方法的思路為:使用給定的鐘差數據L(0)={l(0)(i)，i=1，2，…，n}對 GM(1，1)進行建模，然后利用該GM(1，1)模型擬合L(0)得到擬合鐘差值L1，再用 L(0)減去 L1得到擬合誤差 V，利用GM(1，1)預報后面的鐘差值P1，同時根據擬合誤差V確定適合其預報的小波神經網絡模型并根據確定后的模型預報后續對應誤差V1，最后將GM(1，1)得到的預報值P1與小波神經網絡得到的預報值V1相加得到最終的預報鐘差值。

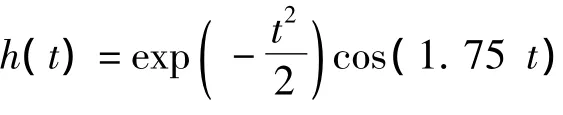
2 算例與分析

使用2013-01-21～22 IGS提供的15 min采樣率的精密鐘差數據進行實驗。該時間段內的GPS星載原子鐘有6種類型:ⅡA銫鐘、ⅡA銣鐘、ⅡR銣鐘、ⅡR-M銣鐘、ⅡF銫鐘和ⅡF銣鐘，隨機選取每種類型鐘所對應的一顆衛星進行實驗，本文選取的衛星有 PRN09、PRN32、PRN19、PRN15、PRN24 和PRN25。為分析所建模型(記為GMWN)的預報性能，同時使用二次多項式模型(QP模型)和GM(1，1)進行相應的鐘差預報，對比各種模型的預報結果;以IGS精密鐘差數據為參照數據，使用預報誤差的最大值和最小值對比模型預報結果的穩定性，使用預報誤差的平均值和均方根對比模型預報結果的精度。其中預報誤差均方根的計算公式為:

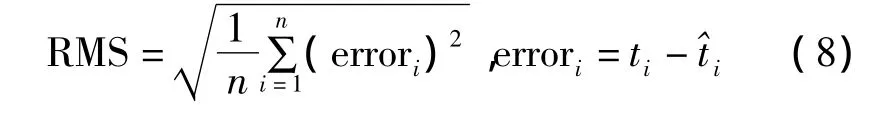
式中errori為預報誤差，^ti、ti為i時刻的IGS精密鐘差值和鐘差預報值，n為預報歷元數。

方案一:使用21日前12 h(48歷元)鐘差數據對3種方法進行建模，預報該天接下來的12 h(48歷元)的鐘差，并對比6顆衛星使用3種方法時的預報效果，如圖1和表1所示。考慮到篇幅所限，這里僅給出PRN24和PRN25(分別代表星載銫鐘和星載銣鐘)的鐘差預報結果對比圖，其余星載原子鐘的預報結果在統計表中給出。方案二的情況類似。

方案二:使用21日前12 h(48歷元)鐘差數據對3種方法進行建模，預報接下來的24 h(96歷元，21日后12 h和22日前12 h)的鐘差，并對比6顆衛星使用3種方法時的預報效果，如圖2和表2。

根據計算結果可以得出如下結論:

1)從兩顆衛星的鐘差預報結果圖中可以明顯看出，隨著預報時間的增加，二次多項式模型的鐘差預報誤差不斷變大，而其余兩種模型的預報結果則相對穩定。

2)在兩個預報方案中，對比星載銣鐘(PRN15、19、25、32)和星載銫鐘(PRN09、24)預報結果的均方根和平均值可知，銣鐘的預報精度總體上要好于銫鐘;而從表征預報結果穩定性的預報誤差最大最小值可以看出，星載銣鐘預報誤差的最大最小值之差小于銫鐘，說明銣鐘的預報結果穩定性優于銫鐘。因此，對于GPS系統的星載原子鐘而言，銣鐘的預報性能總體上要好于銫鐘。而對比星載ⅡA銫鐘和ⅡF銫鐘預報結果的統計值可以看出，銫鐘里面ⅡF銫鐘在預報的穩定性和預報精度方面均好于ⅡA銫鐘，這是由于載有銫鐘的GPSⅡA衛星是系統早期發射的，由于長時間的運行和銫鐘本身的時頻特性使得該類型星鐘的預報性能變差;而后來發射的ⅡF銫鐘預報性能則相對較好。

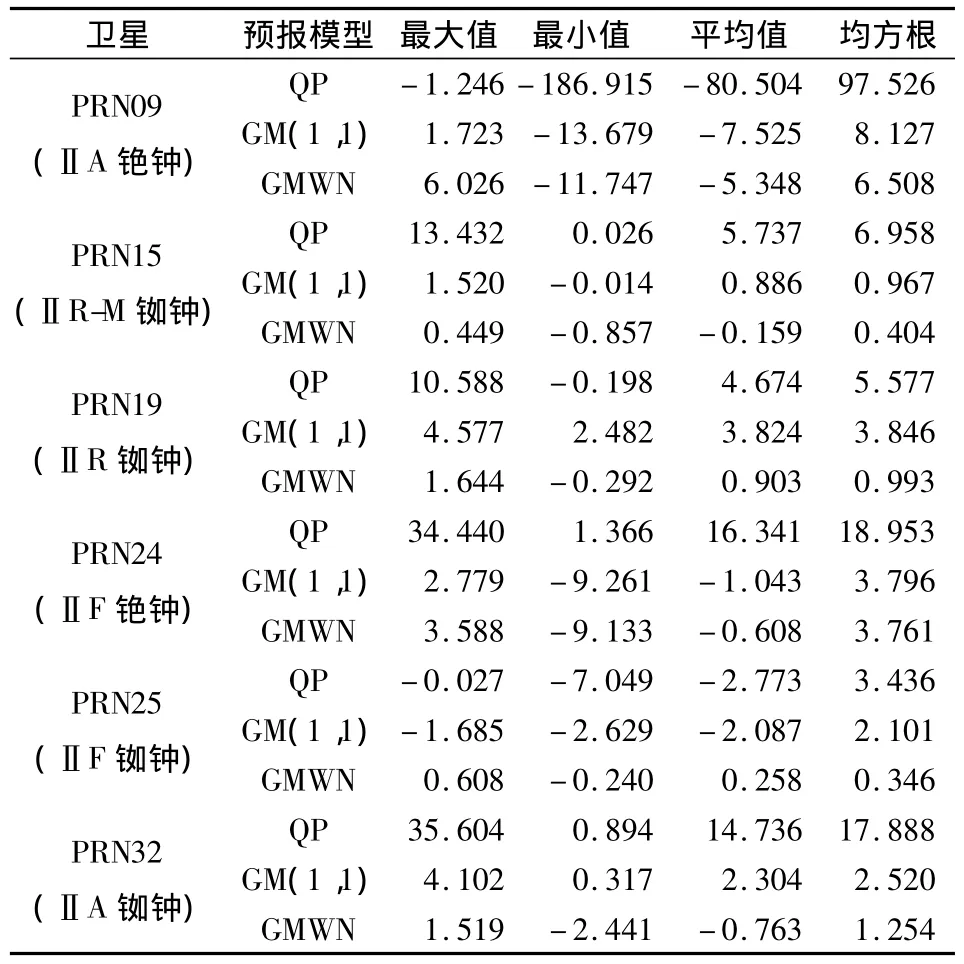
表2 24 h的預報結果統計(單位:ns)Tab.2 The statistics of prediction result in 24 h(unit:ns)

3)對比兩種方案中6顆衛星分別使用3種方法的預報結果統計數據可知，本文方法預報結果的精度優于兩種常用模型，特別是對于ⅡR銣鐘和ⅡF銣鐘。在預報結果穩定性方面，相對于銣鐘(PRN15、19、25、32)而言，本文方法穩定性最好;而對于銫鐘，預報誤差的最大最小值之差分別為:方案一、二中的 PRN09 星，QP 模型為 66.704、185.669 ns，GM(1，1)模型為 11.551、15.402 ns，GMWN 為14.908、17.773 ns;PRN24 星，QP 模型為 15.416、33.074 ns，GM(1，1)模型為 2.820、12.040 ns，GMWN 為3.090、12.721 ns。可以看出，在銫鐘預報穩定上，本文方法與GM(1，1)相當，優于二次多項式模型。

4)由于星載原子鐘自身復雜的時頻特性和極易受外界環境影響的特點，通常使用單一的預報模型來進行鐘差預報有一定的局限性，而組合模型一般情況下可以改善單一模型的不足。

3 結語

基于灰色模型與小波神經網絡相結合的鐘差預報方法，既充分利用了灰色模型和小波神經網絡的優點，又彌補了灰色模型的不足，同時避免了構造復雜的神經網絡結構。實驗結果證明，本文所建模型優于兩種常用模型。

需要說明的是，鐘差預報模型的預報性能還與星載鐘的類型有關。因此，針對不同類型的原子鐘建立相應的預報性能更優的模型是下一步需要研究的問題。

1 Wang Jigang，et al.Prediction of clock errors of atomic clocks based on modified linear combination model［J］.Chinese Astronomy and Astrophysics，2011，35:318 －326.

2 Mishra A，Shenyblat L.Multipath and satellite clock bias error minimization in DGPS based radiolocation［C］.EUROCOMM 2000，IEEE/AFCEA，2007.

3 王宇譜，等.一種新的導航衛星鐘差預報與內插方法［J］.大地測量與地球動力學，2013(4):112－116.(Wang Yupu，et al.A new method of navigation satellite clock bias prediction and interpolation［J］.Journal of Geodesy and Geodynamics，2013(4):112 －116)

4 王穎，徐波，楊旭海.一種利用泛函網絡進行導航衛星鐘差預報的方法研究［J］.宇航學報，2012，33(10):1 401 －1 406.(Wang Ying，Xu Bo，Yang Xuhai.Research on the navigation satellite clock error prediction using functional network［J］.Journal of Astronautics，2012，33(10):1 401 －1 406)

5 黃觀文，楊元喜，張勤.開窗分類因子抗差自適應序貫平差用于衛星鐘差參數估計與預報［J］.測繪學報，2011，40(1):15 － 21.(Huang Guanwen，Yang Yuanxi，Zhang Qin.Estimate and predict satellite clock error using adaptively robust sequential adjustment with classified adaptive factors based on opening windows［J］.Acta Geodaetica et Cartographica Sinica，2011，40(1):15 －21)

6 鄭作亞，等.附有周期項的預報模型及其在GPS衛星鐘差預報中的應用研究［J］.天文學報，2010，51(1):95－102.(Zheng Zuoya，et al.Prediction model with periodic item and its application to the prediction of GPS satellite clock bias［J］.Acta Astronomica Sincia，2010，51(1):95 －102)

7 郭海榮.導航衛星原子鐘時頻特性分析理論與方法研究［D］.鄭州:信息工程大學，2006.(Guo Hairong.Study on the analysis theories and algorithms of the time and frequency characterization for atomic clocks of navigation satellite［D］.Zhengzhou:Information Engineering University，2006)

8 崔先強，焦文海.灰色系統模型在衛星鐘差預報中的應用［J］.武漢大學學報:信息科學版，2005，30(5):447 －450.(Cui Xianqing，Jiao Wenhai.Grey system model for the satellite clock error predicting［J］.Geomatics and Information Science of Wuhan University，2005，30(5):447 －450)

9 鄭作亞，陳永奇，盧秀山.灰色模型修正及其在實時GPS衛星鐘差預報中的應用研究［J］.天文學報，2008，49(3):306 － 320.(Zheng Zuoya，Chen Yongqi，Lu Xiushan.An improved grey model for the prediction of real-time GPS satellite clock bais［J］.Acta Astronomica Sincia，2008，49(3):306－320)

10 王宇譜，等.衛星鐘差預報的小波神經網絡算法研究［J］.測繪學報，2013，42(3):323 －330.(Wang Yupu，et al.Research the algorithm of wavelet neural network to predict satellite clock bias［J］.Acta Geodaetica et Cartographica Sinica，2013，42(3):323 －330)

11 楊華龍，劉金霞，鄭斌.灰色預測GM(1，1)模型的改進及應用［J］.數學的實踐與認識，2011，41(23):39 －46.(Yang Hualong，Liu Jinxia，Zheng Bin.Improvement and application of grey prediction GM(1，1)model［J］.Mathematics in Practice and Theory，2011，41(23):39 －46)

12 唐校，等.基于最小二乘法的灰色模型參數估計［J］.湘南學院學報，2010，31(5):62 － 64.(Tang Xiao，et al.Parameter estimation of gray model based on least squares method［J］.Journal of Xiangnan University，2010，31(5):62－64)

13 萬李，楊杰.小波神經網絡在短時交通流量預測中的應用［J］.計算機仿真，2012，29(9):352 － 355.(Wan Li，Yang Jie.Application of wavelet neural network to prediction of short time traffic flow［J］.Computer Simulation，2012，29(9):352 －355)

14 Tabaraki R，Khayamian T，Ensafi A A.Solubility prediction of 21 azo dyes in supercritical carbon dioxide using wavelet neural network［J］.Dyes and Pigments，2007，73:230 －238.

15 王繼剛.基于GPS精密單點定位的時間比對與鐘差預報研究［D］.北京:中國科學院研究生院，2010.(Wang Jigang.Research on time comparison based on GPS precise point positioning and atomic clock prediction［D］.Beijing:Graduate School of CAS，2007)

A METHOD OF SATELLITE CLOCK BIAS PREDICTION BASED ON GRAY MODEL AND WAVELET NEURAL NETWORK

Wang Yupu，Lü Zhiping，Chen Zhengsheng and Huang Lingyong
(Institute of Geo-Spatial Information，Information Engineering University，Zhengzhou 450052)

A new prediction method based on the combination of gray system model and wavelet neural network is proposed.Firstly，fitting given satellite clock bias values with gray model，and determining parameters of gray model with the values.Then，establishing model of wavelet neural network with fitting residuals.Finally，combining the prediction results obtained from the two models mentioned above to get prediction results.The results of prediction tests using the precise satellite clock bias data from IGS show that the method can get better satellite clock bias prediction results，compared to the quadratic polynomial model and the grey model.Especially for the rubidium clock ofⅡR type and ⅡF，the prediction precision can be provided with two times or more.

satellite clock bias prediction;gray model;wavelet neural network;Inertial Guidance System(IGS);combination prediction model

P228.41

A

1671-5942(2014)03-0155-05

2013-08-22

國家自然科學基金項目(41274015);國家863計劃項目(2013AA122501)。

王宇譜，男，1988年生，碩士研究生，主要研究方向為測量數據處理方法與理論。E－mail:987834660@qq.com。