地鐵浮置式軌道引起地表振動響應解析預測模型研究

吳宗臻，劉維寧，馬龍祥，王文斌

（1．北京交通大學 土木建筑工程學院，北京 100044；2．鐵科院（北京）工程咨詢有限公司，北京 100081）

城市軌道交通的飛速發展在改善城市交通擁堵的同時，也引起了越來越嚴重的環境振動問題［1］。為了降低地鐵列車運行對周圍環境的振動影響，各類減振產品廣泛應用于地鐵各線的減振區段。其中浮置式軌道具有固有頻率低，減振效果好，不影響輪軌工作性能等優點，主要結構型式有鋼彈簧浮置板軌道［2］、橡膠浮置板式軌道［3］（浮置式道床軌道）和梯式軌枕軌道［4］（浮置式軌枕軌道）等。我國現行《環境影響評價技術導則——城市軌道交通》［5］推薦采用統一的經驗鏈式公式作為環境振動預測計算方法，該方法簡單快捷，普適性強，（但是精度較低且無法在頻域內進行定量預測。尤其對于采用浮置式軌道的環境振動敏感區段，往往對振動頻譜有特殊的要求，規范推薦的Z振級預測公式已經不能滿足實際應用要求。而且隨著城市軌道交通路網越來越密集，沿線的敏感目標也會大量增加，現有的地鐵環境振動的頻域內解析和數值預測方法往往計算周期較長，無法適用于同時精確高效的預測地鐵沿線多個敏感目標的環境振動［6］。因此，環境振動評價亟須要一種滿足頻域預測精度要求且快速高效的預測方法進行輔助決策。

針對地鐵環境振動多點同步快速預測問題，提出了一種適用于區間地鐵引起環境振動的頻域快速預測模型，將浮置式軌道環境振動問題轉化為通過浮置式軌道模型［7］求解作用于基底的頻域力群和通過地表振動響應的三維Green函數［8］求解土層頻響函數群，然后將兩者進行頻域內復數疊加運算得出地表的振動響應。采用本模型預測了北京地鐵4號線浮置板區間地表振動響應，并與現場地表振動實測數據進行對比分析，驗證了該模型的可行性和準確性。本模型具有較高的預測精度和較快的計算速度，可用于預測地鐵建設設計階段的地鐵運行引起的環境振動的加速度時程，頻譜，1／3倍頻程與Z振級。

1 模型基本原理及預測流程

對于地鐵列車引起的振動傳播系統，國內外學者通常將其視為線彈性系統，對于土層也多是將其簡化為水平成層線彈性體［9－10］。實測表明，地鐵運行引起的環境振動的量級較小，土層處于彈性應變階段［11］。因此，本模型將土層系統簡化為水平成層彈性體。

對于線彈性的系統，任意兩點間的振動傳遞規律是系統的固有特性，不同頻率處的振動傳遞性質不因振源輸入的不同而改變。地表振動響應Green函數描述了在半無限空間成層土體內部的單位脈沖激勵作用下的地表振動響應，通過Green函數可以求得土體內部某點作用一垂向單位脈沖荷載的地表測點處的振動響應，稱之為土層振動頻響函數。本預測模型即將車軌模型作用于基底的頻域力與該點處頻率響應函數進行運算，從而利用線彈性系統振動傳遞特性來的達到預測地表振動的目的。

整個預測模型實現過程分為三個主要步驟：

第一步，本預測模型通過解析的方法求解出浮置式軌道系統作用于基底的頻域力群F＾n（ω），將列車運行的復雜時空效應轉化為固定系列點荷載輸入，如圖1所示。

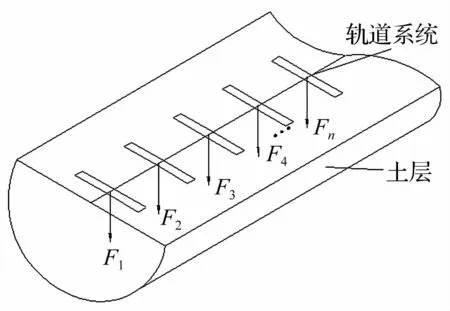
圖1 軌道模型求解的基底頻域力群Fig．1 Forces on base calculated by track model

第二步，采用成層土體三維Green函數求解出基底頻域力群（ω）作用點處到地表預測點處的振動頻響函數群 Hn（ω）。

第三步，將對應位置處的頻域力和頻響函數進行復數相乘運算得到單個固定力輸入的地表預測點的振動響應（ω）×Hi（ω）。最后在頻域內進行復數疊加運算得出頻域力群（ω）作用下地表預測點處的振動響應（ω），即為地鐵列車經過浮置式軌道引起的地表響應，如式（1）所示。

其中：n為計算的基底頻率力的數目，ω為圓頻率，符號“＾”代表頻域內的物理量。

預測模型的基本流程如圖2所示。

圖2 預測模型流程圖Fig．2 Flow chart of prediction model

本模型將地鐵列車運行的時空荷載輸入，變換到與時間無關的頻域內進行求解，整個計算過程都是在頻域內進行的復數運算，頻域力、頻響函數以及最終預測結果都包含了幅值和相位全部信息。通過分解及轉化的思想可以快速的得到地鐵列車在浮置式軌道上運行作用下的環境振動響應。

2 預測模型解析解

2．1 浮置式軌道模型基底力群的求解

為了準確地求解出浮置式軌道系統作用于隧道基底的頻域力 F＾n（ω），需要構建高精度的車軌耦合模型［7，12］（圖 3）。模型中，車輛采用 6節編組，每節車廂有4個輪對、2個轉向架、1個車體，都簡化為剛體，一系、二系彈簧簡化為彈簧阻尼元件。軌道系統為以一個浮置板長為周期的無限長結構，其中，將鋼軌簡化為離散點支撐的無限長歐拉梁，浮置板簡化為離散點支撐的有限長歐拉梁，扣件及隔振器簡化為彈簧阻尼單元。

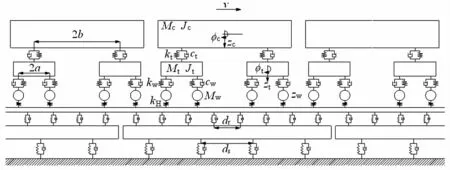
圖3 浮置式軌道車軌耦合模型Fig．3 Coupled train-track model of floating-type track

在求解模型的過程中，輪軌激振形式采用移動荷載狀態激振（車輪在具有不平順的軌道結構上向前移動）［12］，而非傳統的定點荷載狀態激振（車輪不動，輪軌表面不平順的激勵帶反向移動）。

模型的基本求解思路如下：

（1）在采用移動荷載狀態激振的前提下，將軌道不平順表示成系列三角函數的疊加，在單一頻率成分的不平順下，求解對應頻率的輪對柔度矩陣及軌道結構上輪軌接觸點的柔度矩陣，而后耦合車輛系統及軌道系統，求得相應頻率成分的動態輪軌激勵力。

（2）將考慮的所有頻率成分不平順引起的動態輪軌激勵力計算出來并進行疊加，將總輪軌力表示成一系列具有不同頻率成分的簡諧力的疊加。

（3）求解移動簡諧荷載作用下的浮置式軌道系統的動力響應。

（4）將求解出的輪軌力（系列簡諧力的疊加形式）帶入簡諧荷載作用下的浮置式軌道模型的動力響應解答中，從而達到車輛響應及軌道響應的求解，進而得到基底頻域力群。

文獻［12］給出了在移動荷載狀態激振下的輪對相互影響系數的求解方法，這是求解車軌耦合模型的輪軌力的基礎。文獻［7］給出了一種考慮周期性結構基本性質的采用模態疊加技術的數值方法，可以精確快速的求解出浮置式軌道在移動諧振荷載作用下的動力響應。

基于這些成果形成程序STFSTI，計算得到車軌模型動力響應及基底頻域力群F＾n（ω）（圖4）。具體的理論推導過程可以查閱相關參考文獻，此處不再贅述。

圖4 典型基底頻域力Fig．4 Typical force on base in frequency domain

2．2 土層頻響函數群的求解

將土層簡化為水平成層的半無限空間彈性體，每個土層均為各向同性的連續彈性介質（圖5）。土體Green函數［8］表征了在土體內部某一坐標方向上施加一個單位脈沖荷載，在任意一點處產生的振動響應。土層內部脈沖激勵作用下的地表測點處的頻響函數群可以通過求解水平成層土體表面Green函數得到。

圖5 成層半空間土體模型Fig．5 Model of layered half-space soil

采用直接剛度法［13］求解土體Green函數的基本思路如下：

（1）通過積分變換把時間－空間域內的波動方程轉化到頻率－波數域，之后在頻率－波數域內推導出每層土體交界面上的位移和面力。

（2）建立每層土體的剛度矩陣（這個剛度矩陣稱為單元剛度矩陣），即通過剛度矩陣可以建立每層土體上下表面上的面力和位移之間的平衡方程。

（3）把各層土體的單元剛度矩陣集總成一個總剛度矩陣，并建立一個總的平衡方程，解這個平衡方程，可以得到各個土層交界面上的位移，最后通過形函數可以求得每個土層內部的位移和面力。

（4）在土體內部施加垂向脈沖激勵，將垂向脈沖荷載帶入總平衡方程，根據Green函數的定義，此時所求得的土層內部的位移和面力即為土體的Green函數。地表的Green函數解答即為本文需要的土層頻響函數群 Hn（ω）。

3 預測模型的實測驗證

3．1 現場振動加速度實測

為了驗證本預測模型的適用性，選取北京地鐵鋼彈簧浮置板區間進行振源加速度測試，在鋼軌、道床及隧道壁上布置傳感器，測點布置如圖6所示。

圖6 隧道內加速度傳感器布置圖Fig．6 Lacations of sensors in tunnel

另外選取北京地鐵4號線北大東門區間的鋼彈簧浮置板區段進行地表振動加速度測試，地表測點的位置為距離地鐵隧道中心線水平距離30 m處，隧道、土層及地表測點位置關系如圖7所示。

圖7 隧道及土層關系圖Fig．7 Distribution of tunnel and soil

振動測試采用INV3018C型24位高精度數據采集儀以及 Lance系列高精度壓電式加速度傳感器。INV3018C型24位高精度數據采集儀采用24位ΔΣ方式的AD轉換器，結合了最新FPGA和DSP技術，可8個通道并行處理，單個通道最高采樣頻率51．2 kHz，動態范圍120 dB。數據采集及分析軟件為DASP V10。

3．2 浮置板軌道振動加速度驗證

將前文構建的浮置式軌道模型編制Matlab程序進行計算，參數采用鋼彈簧浮置板軌道（FST）實際參數，如表1所示。

圖8～圖9為浮置板上的振動加速度頻譜和1／3倍頻程譜的實測值與計算值的對比。可以看出，計算值與實測值量值相當，變化趨勢相同。結果表明浮置式軌道模型構建及求解過程科學合理，采用其求解出的頻域力群是準確可信的。

表1 軌道參數Tab．1 Track parameters

圖8 浮置板振動加速度頻譜幅值實測與計算值對比Fig．8 Comparison of acceleration frequency spectrum of FST

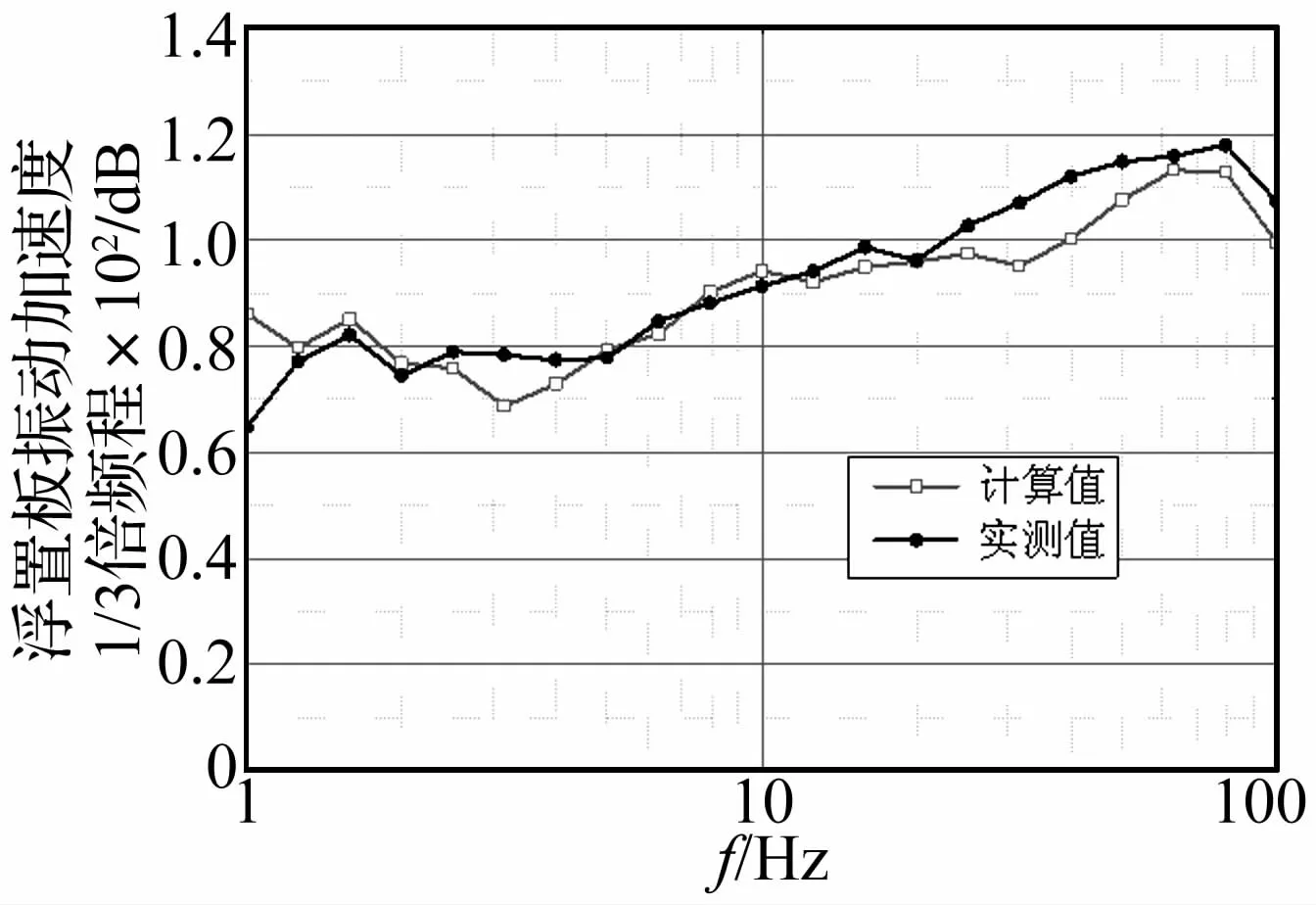
圖9 浮置板振動加速度1／3倍頻程實測與計算值對比Fig．9 Comparison of acceleration one-third octave spectrum of FST

3．3 地表振動加速度驗證

采用本文提出的預測模型編制程序進行地表振動響應預測，土層參數采用北京地鐵4號線北大東門區間實際地勘參數，如表2所示。

表2 土層參數Tab．2 soil parameters

圖10為輸入實際地勘土層參數的三維Green函數計算得到的頻響函數群中，距離脈沖水平距離40 m和100 m處的典型頻譜幅值。可以看出，土層地表頻響函數隨著頻率的增加呈現“波浪形”變化趨勢，而且100 m處的響應在全頻帶都比40 m處的響應量值有很大的降低。這說明隨著距離脈沖位置水平距離的增加，土體對頻域內振動的傳播具有很強的衰減效果。

圖11～圖12為地表振動加速度頻譜和1／3倍頻程譜的實測值與計算值的對比。可以得出：

（1）模型預測和實測地表振動加速度的頻譜波形相近，量級相當，振動主頻都在8～10 Hz的鋼彈簧浮置板的固有頻率附近，而且兩者的頻域振動幅值相當。在35～50 Hz頻段現場實測頻譜有除了8 Hz自振頻段峰值外的第二個小峰值群，計算值在此頻段偏小。

（2）模型計算值和實測值的1／3倍頻程譜曲線基本重合，振動量級、變化趨勢一致。在40 Hz頻帶計算值稍低，這與頻譜分析結果相符。

（3）Z振級計算結果為：地表實測Z振級54．0 dB，預測模型計算Z振級為56．1 dB，預測結果偏于安全且誤差較小。

圖10 地表振動加速度頻響函數幅值Fig．10 Acceleration frequency response functions of ground points

圖11 地表振動加速度頻譜幅值實測與計算值對比Fig．11 Comparison of ground acceleration frequency spectrum

圖12 地表振動加速度1／3倍頻程實測與計算值對比Fig．12 Comparison of ground acceleration one－third octave spectrum

由于本預測方法旨在頻域內解決地鐵環境振動評價中的多點同時、快速準確預測問題，為了可以采用解析的方法求解土層頻響函數從而提高計算速度，本預測模型采用Green函數法求解土層頻響函數群。因為Green函數法是針對水平成層彈性體振動響應的純解析模型，無法引入隧道結構進行解析求解，因此本模型在求解土層頻響函數時進行了簡化，忽略掉了隧道結構的影響。由本模型計算結果與實測的對比分析可以看出，在簡化了隧道結構對振動的影響下，振動預測結果是較為精確的。說明本模型做出的這個簡化是合理的，取得了地鐵環境振動預測中計算速度和預測精度的平衡。

4 結 論

在土層振動傳遞固有特性的基礎上，針對地鐵建設設計階段的多點快速預測要求，提出了一種浮置式軌道引起地表振動響應的頻域解析預測模型，利用求解浮置式軌道作用于基底的頻域力群和土層振動頻響函數群的方法來預測地鐵浮置式軌道引起的地表振動響應。

本模型通過優化的解析解編程實現，采用符合實際動力特性的浮置式軌道模型與考慮實際土層中振動傳播特性的三維Green函數求解頻響函數，保證了模型預測的精度，且相比其他動力仿真模型具有極快的計算速度，可在設計階段同時針對有高等級特殊減振需求的多個敏感點地鐵區間開展浮置式軌道選型工作。

采用本模型預測了北京地鐵4號線浮置板區間地表振動響應，并與現場實測進行對比驗證，表明本模型具有預測速度快、預測精度高、預測頻帶寬等特點，可有效預測浮置式軌道區間的地鐵列車運行引起的地表振動響應，從而合理選擇減振軌道型式。本模型具有重大的工程應用和社會價值，是現有環評預測方法的有效補充。

［1］夏禾，曹艷梅．軌道交通引起的環境振動問題［J］．鐵道科學與工程學報，2004，1（1）：44－51．XIA He，CAO Yan-mei．Problem of railway traffic induced vibration of environments［J］．Journal of Railway Science and Engineering，2004，1（1）：44－51．

［2］張寶才，徐禎祥．螺旋鋼彈簧浮置板隔振技術在城市軌道交通減振降噪上的應用［J］．中國鐵道科學，2002，23（3）：68－71．ZHANG Bao-cai，XU Zhen-xiang．Applications of the steel spring floating track bed for vibration and noise control in urban rail traffic［J］．Journal of China Railway Science，2002，23（3）：68－71．

［3］劉洪瑞，鄒錦華，王榮輝．軌道交通橡膠浮置板式軌道結構動力設計參數研究［J］．鐵道科學與工程學報，2009，6（2）：5－11．LIU Hong-rui，ZOU Jin-hua，WANG Rong-hui．Dynamic design parameters of rubber floating slab track structure for urban mass transit［J］．Journal of Railway Science and Engineering，2009，6（2）：5－11．

［4］金浩，劉維寧．蟻群算法耦合LS-DYNA梯式軌枕軌道動力特性優化［J］．振動與沖擊，2013，32（2）：24－28．JIN Hao，LIU Wei-ning．Optimization of laddertype track using ant colony algorithm coupled with LS-DYNA［J］．Journal of Vibration and Shock，2013，32（2）：24－28．

［5］中華人民共和國環境保護部．HJ453－2008．環境影響評價技術導則——城市軌道交通［S］．北京：中國環境科學出版社，2008．

［6］劉維寧，馬蒙，王文斌．地鐵列車振動環境響應預測方法［J］．中國鐵道科學，2013，34（4）：110－117．LIU Wei-ning， MA Meng， WANG Wen-bin． Prediction method for subway train-induced environmental vibration responses［J］．Journal of China Railway Science，2013，34（4）：110－117．

［7］馬龍祥，劉維寧，李克飛．移動荷載作用下浮置板軌道振動響應的頻域快速數值算法［J］．鐵道學報，2014，36（2）：86－94．MA Long-xiang，LIU Wei-ning，LI Ke-fei．Fast numerical algorithm of floating slab track vibration response under moving loads in the frequency domain［J］．Journal of the China Railway Society，2014，36（2）：86－94．

［8］Schevenels M． The impact of uncertain dynamic soil characteristics on the prediction of ground vibrations［D］．Leuven：K．U．Leuven，2007．

［9］Degrande G，Clouteau D，Othman R，et al．A numerical model for ground-borne vibrations from underground railway traffic based on a periodic finite element-boundary element formulation［J］．Journal of Sound and Vibration，2006，293（3－5）：645－666．

［10］劉衛豐．地鐵列車運行引起的隧道及自由場動力響應數值預測模型研究［D］．北京：北京交通大學，2009．

［11］王文斌．基于脈沖實驗的地鐵環境振動響應傳遞函數預測方法研究［D］．北京：北京交通大學，2011．

［12］馬龍祥，劉維寧，李克飛．浮置板軌道上輪對相互影響系數的求解［J］．中南大學學報（自然科學版），2013，44（12）：5068－5074．MA Long-xiang， LIU Wei-ning， LI Ke-fei． Calculation method of wheelsetsinteraction coefficient on floating slab track［J］．Journal of Central South University（Science and Technology），2013，44（12）：5068－5074．

［13］Kausel E． Fundamental solutions in elastodynamics： a compendium［M］．New York：Cambridge University Press，2006：140－184．