基于特高頻譜圖統計參量的局部放電定位方法研究

彭超， 阮江軍， 黃道春， 雷清泉，3， 周瑜

(1.武漢大學電氣工程學院，湖北武漢 430072;2.中國電力科學研究院，湖北武漢 430074;3.哈爾濱理工大學電氣與電子工程學院，黑龍江哈爾濱 150080;4.國網青海省電力公司電力科學研究院，青海西寧 810008)

0 引言

絕緣材料在電力設備中普遍存在，是保證電力設備尤其是高壓電力設備正常運行的重要組成部分，但是由于長期處于電場、機械振動、環境等因素作用下，絕緣材料發生著緩慢的老化。在電力設備運行過程中，由于絕緣材料本身老化、加工缺陷、安裝失誤等因素，均會在絕緣材料內部產生局部放電，而局部放電的產生又會加速絕緣材料的老化，有些極端情況下，會迅速導致絕緣材料擊穿，引發電力設備故障，帶來不同程度的經濟損失。由于局部放電對高壓電力設備的危害，有必要進行局部放電測量、檢測和定位以確定電力設備的絕緣狀態。

特高頻(ultra－high frequency，UHF)檢測技術是一種利用微波天線檢測局部放電激發的電磁波信號的局部放電檢測技術，自從英國學者Hampton B F于20世紀80年代將該技術應用到GIS局部放電檢測以來［1－2］，特高頻檢測技術憑借較強的抗干擾能力，較高的信噪比，有著巨大的應用價值，因此推動了特高頻檢測技術的發展。目前，對特高頻檢測技術的研究涉及了局部放電研究的眾多領域，包括電力設備中電磁波傳播特性研究［3－5］、局部放電特高頻電磁波特性研究［5］、局部放電定位、局部放電識別［6－7］、特高頻天線的研制［8］、特高頻監測裝置的研制［9－10］等等。

局部放電定位能夠為基于狀態的檢修策略提供有的放矢的檢修位置，受到現場工作人員及科研人員的重點關注。目前基于特高頻的局部放電定位技術多采用基于時間差的定位方法，其基本思想是通過計算電磁波到達多個傳感器的時間差，聯立求解時間差方程組，再通過空間搜素從而確定局部放電源位置。在基于時間差進行局部放電定位研究方面，國內外學者尤其是國內學者做出了大量貢獻，如清華大學高文勝等人改進了確定時延的方法，采用了特高頻法和信號傳播時延來實現對局部放電源的定位，該法采用信號初始峰值法、相關法和能量最小值法求取信號傳播時延，并通過比較確定了一套求取時延的方案［11］。文獻［12］提出了雙譜時延估計的理論基礎，給出了參數化雙譜時延估計算法的數值實現步驟，并用實驗驗證了方法的有效性。文獻［13］均對基于時間差的定位算法、時間延遲等關鍵問題進行研究，并通過實驗的方式確定了其方法的有效性。

然而，基于時間差的超高頻局部放電定位方法最根本的計算參數是時間差，時間差是影響定位精度的決定因素，而要獲得時間差往往需要采集設備達到ns級的精度并保證精確的時間同步，這對硬件設備和成本都要求很高，所以本文嘗試引入一種新的基于距離的局部放電定位方法，并且可以應用于離線檢測、帶電檢測和在線監測。

1 實驗平臺

首先建立特高頻局部放電測量系統，包括微帶全向天線、檢波器、數字示波器、計算機等設備。其中數字示波器用于電磁波信號單次波形采集和統計譜圖的采集，計算機用于電磁波信號單次波波形特征量和統計譜圖統計參量的提取。圖1為特高頻局部放電測量和數據采集系統接線圖，圖2為系統框圖。

實驗中同時采集局部放電產生的超高頻電磁波單次放電信號和150個工頻周期的統計波形，測量系統包括微帶全向天線、檢波器、數字示波器、計算機。實驗中使用微帶天線，在距離放電源不同位置處采集電磁波信號。局部放電測量系統包括局部放電模型，無局放變壓器，耦合電容和保護電阻、微帶全向天線、數字示波器、計算機。其中數字示波器用于電磁波信號單次波形測量的測量。局部放電電磁波測量和數據采集系統接線圖如圖2所示。

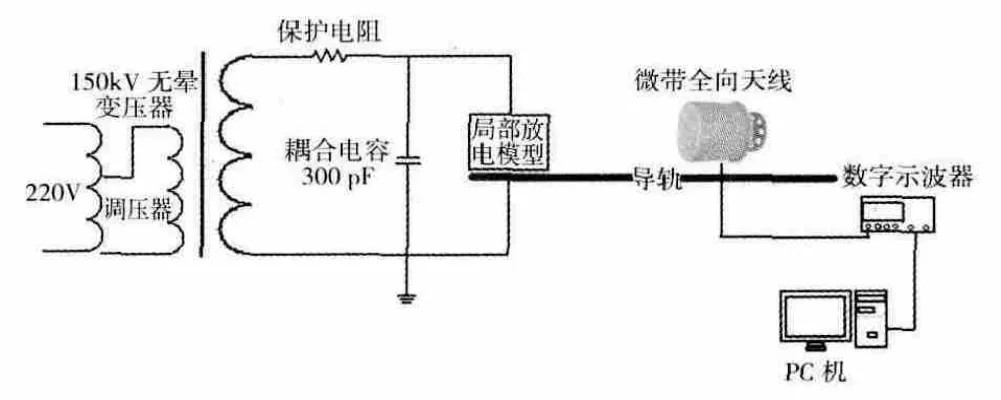
圖1 局部放電試驗系統Fig.1 Pairtial discharge experimental system

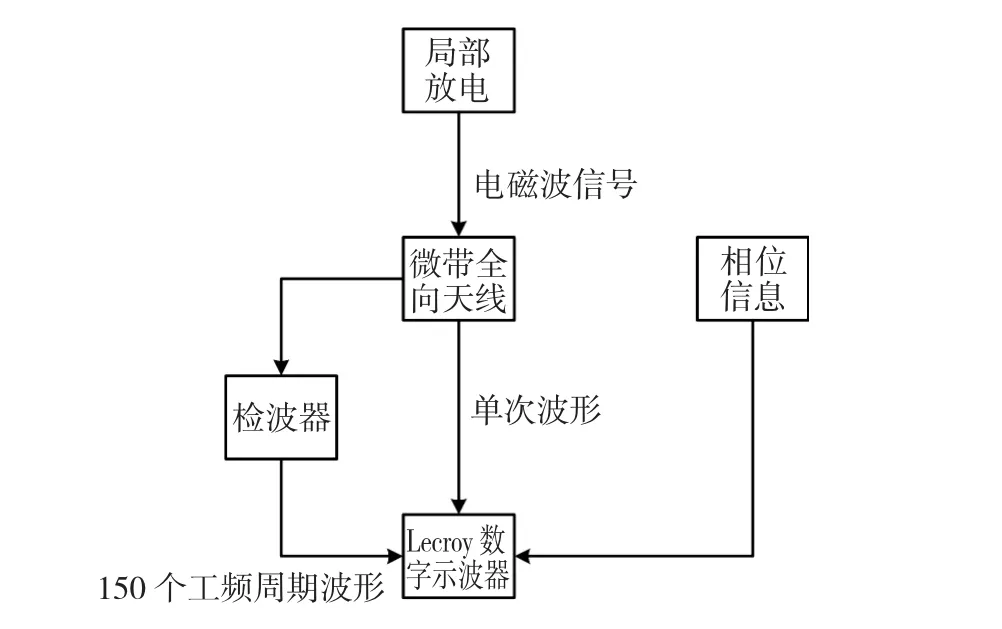
圖2 實驗測量系統框圖Fig.2 Block diagram of experimental measurement system

工頻高壓由YDTW15/150 kV無暈工頻高壓試驗變壓器提供，高壓的輸出端串聯一個10MQ的保護電阻，以免試品后電流過大損毀變壓器，高壓端為兩個表面光滑的鋁質均壓環，中間可以引出高壓導線。保護電阻與主變壓器之間為活動連接，底座上均有滑輪，可以布置在任何方位上。整個設備連接處和設備內部都做了防電暈處理，整體放電量小于5 pC。數字示波器為LecroyLC574A示波器，示波器共有4路輸入通道，最高采樣率為20 GS/s，其工作頻帶為0～1 GHz，存儲深度32 MB。由于本文的研究內容是基于特高頻特征參量進行局部放電定位，故設計了一個導軌用于放置全向微帶天線，導軌上標注有放電源的位置以及距離放電源的距離。同時為了不同放電類型其特征參量與檢測距離的關系，本文設計了兩種局部放電類型，分別是氣隙放電和懸浮放電。

2 測量距離對局部放電電磁波統計特征參量的影響

本節通過研究統計參量與檢測距離的關系，尋找與距離相關的特征參量。

2.1 特征參量的選取

國內外學者，尤其是國內學者［7，14－16］對特高頻信號的特征參量選取展開了大量的研究，選取了多種非常有效的特征參量，這些特征參量包括時域特征和頻域特征，如西安交通大學的成永紅等人提出了基于小波分解的分形維數［16］、重慶大學的孫才新、唐炬等人利用小波和復小波變換有效提取特高頻特征參量［7，17］、上海交通大學李立學等人獲得了5種典型缺陷的特高頻包絡信號數據并采用這種方法實現了96%以上的識別精度［18］。然而由于現場應用中受到成本和采樣率的限制，目前工程應用中基于特高頻的特征參量主要采用局部放電統計譜圖和譜圖統計參量作為局部放電檢測的特征參量［19］，故本文選取的特征參量為局部放電統計譜圖的統計參量，具體如表1所示。本文中采用的局部放電譜圖除了經常使用的最大放電幅值—相位譜圖(Hqmax(φ))，平均放電幅值—相位譜圖(Hqn(φ))和放電次數—相位譜圖(Hn(φ))以外，還引入了密度譜圖［20］，即將放電次數n作為最大放電幅值qmax(H(qmax)［n］)和平均放電幅值qn(H(qn)［n］)的函數。

表1 二維PRPD譜圖統計候選參量Table 1 Candidate statistical parameters of PRPD

2.2 檢測距離對統計特征參量的影響

本文采集樣本數如表2所示。所研究的統計參量為5種統計譜圖的偏斜度、峭度和相關度(表1)。

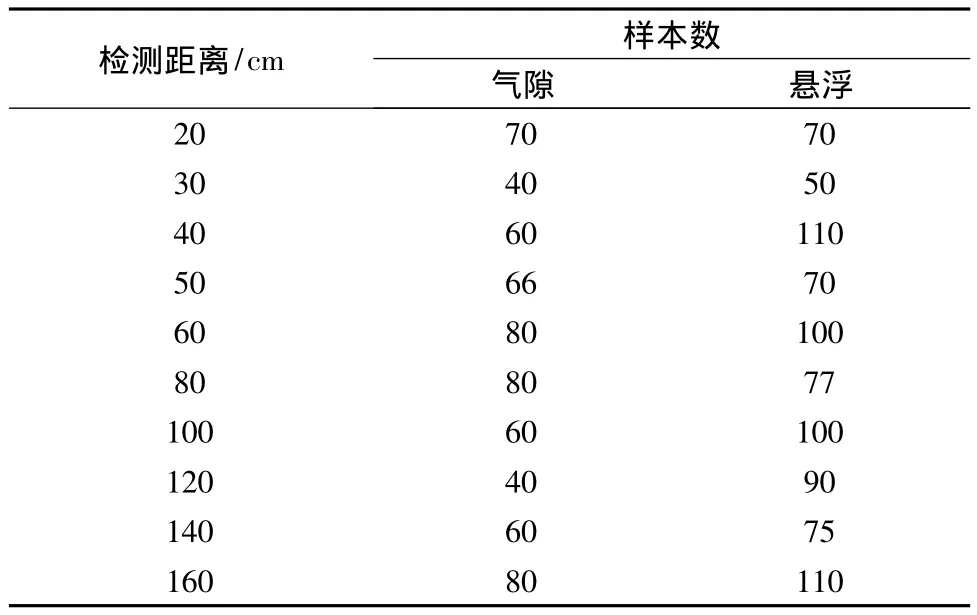
表2 不同檢測距離下局部放電PRPD譜圖樣本數Table 2 The number of PRPD samples at different detection distance

2.2.1 檢測距離對偏斜度的影響

對于氣隙放電而言，Hqmax(φ)譜圖的正負半周偏斜度變化趨勢基本一致，當檢測距離為8 cm時，正負半周均值大約是其他位置測量偏斜度的一半，其他測量位置的偏斜度均值大約維持在2左右。對于懸浮放電而言，正負半周的變化趨勢與氣息放電基本相同，但是懸浮放電正半周的值大于氣隙放電正半周偏斜度，而負半周值小于氣隙放電類型的負半周值(圖3)。

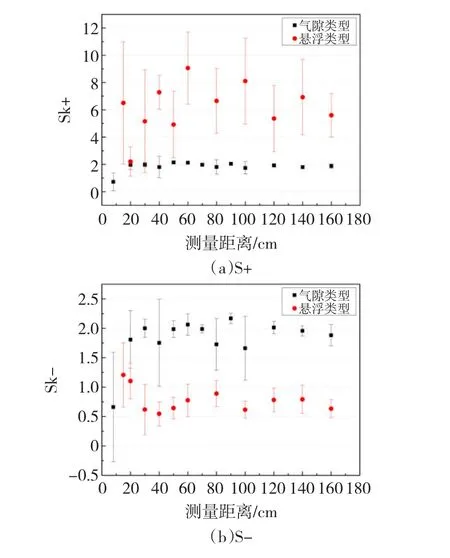
圖3 Hqmax(φ)中Sk均值和方差隨檢測距離增加的變化趨勢Fig.3 The tendency of Sk in Hqmax(φ)along with the detection distance

對于Hqn(φ)和Hn(φ)(圖4和圖5)，兩種放電類型的偏斜度與檢測距離的變化關系不相同，且懸浮放電的偏斜度均小于同類型譜圖中的氣隙放電的偏斜度，而且兩種類型的偏斜度隨監測距離的變化趨勢不相同，即在20 cm處，氣隙放電的偏斜度增大，而懸浮放電的偏斜度減小。

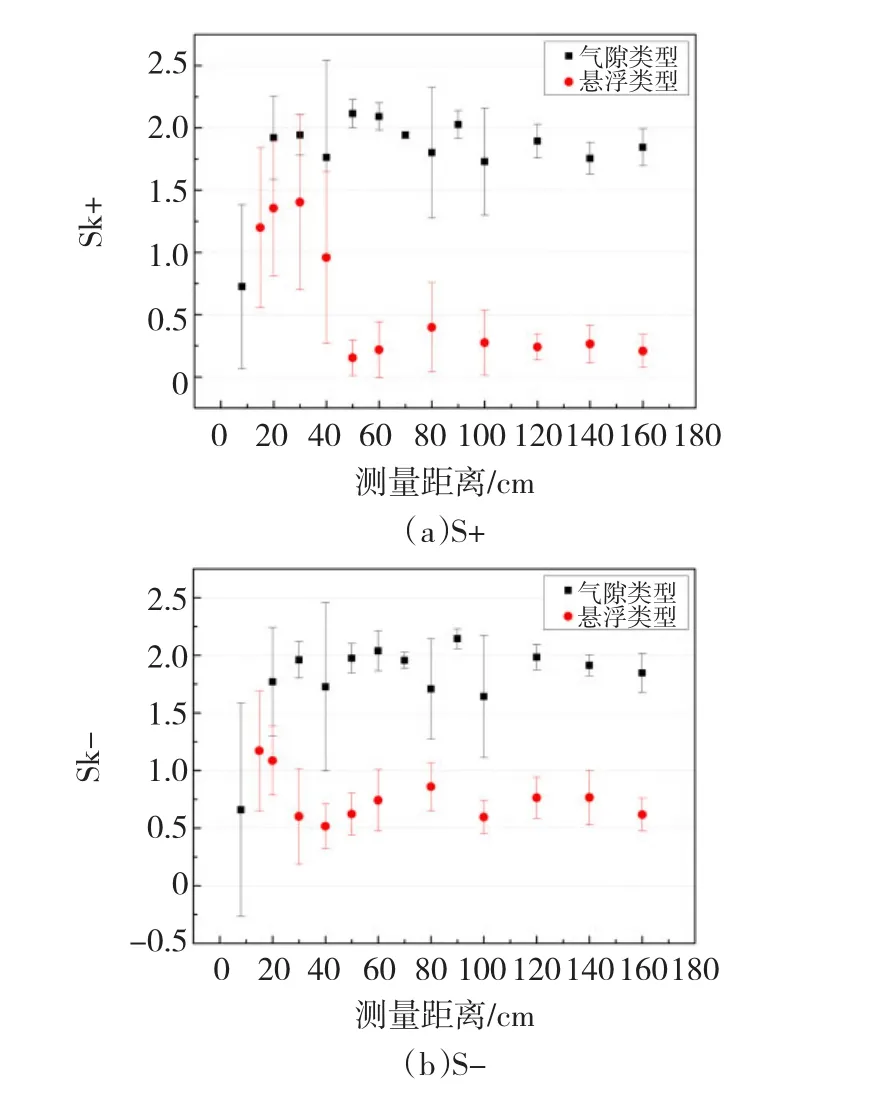
圖4 Hqn(φ)Sk均值和方差隨檢測距離增加的變化趨勢Fig.4 The tendency of Sk in Hqmax(φ)along with the detection distance

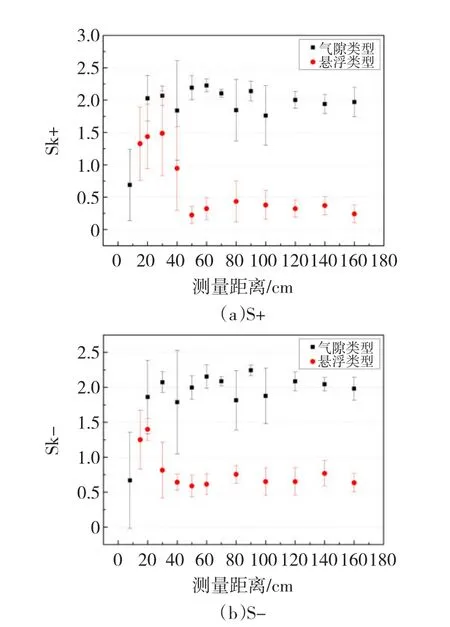
圖5 Hn(φ)Sk均值和方差隨檢測距離增加的變化趨勢Fig.5 The tendency of Sk in Hn(φ)along with the detection distance

相比上述3種譜圖，2種放電類型H(qmax)［number］和H(q)［number］的偏斜度值和變化趨勢基本一致(見圖6和圖7)。

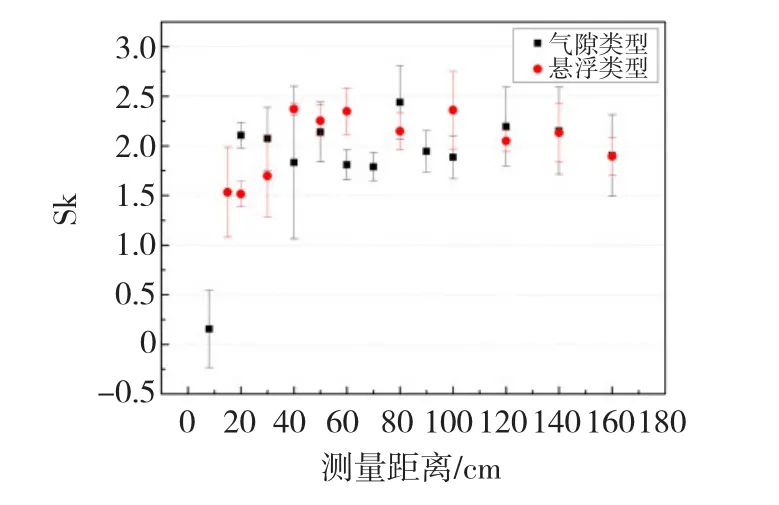
圖6 H(qmax)［n］Sk均值和方差隨檢測距離增加的變化趨勢Fig.6 The tendency of Sk in H(qmax)［n］along with the detection distance

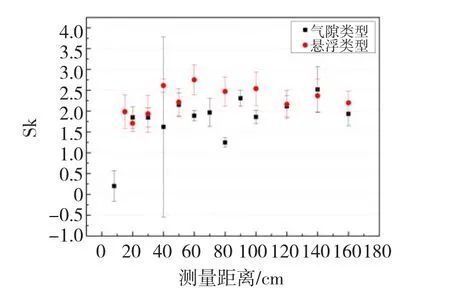
圖7 H(qn)［n］Sk均值和方差隨檢測距離增加的變化趨勢Fig.7 The tendency of Sk in H(qn)［n］along with the detection distance

2.2 .2檢測距離對峭度的影響

對氣隙放電而言，當檢測距離為8 cm時，峭度的均值遠小于其他位置測量得到的峭度，其他測量位置的峭度均值在2～8的區間內變化，如圖8所示。

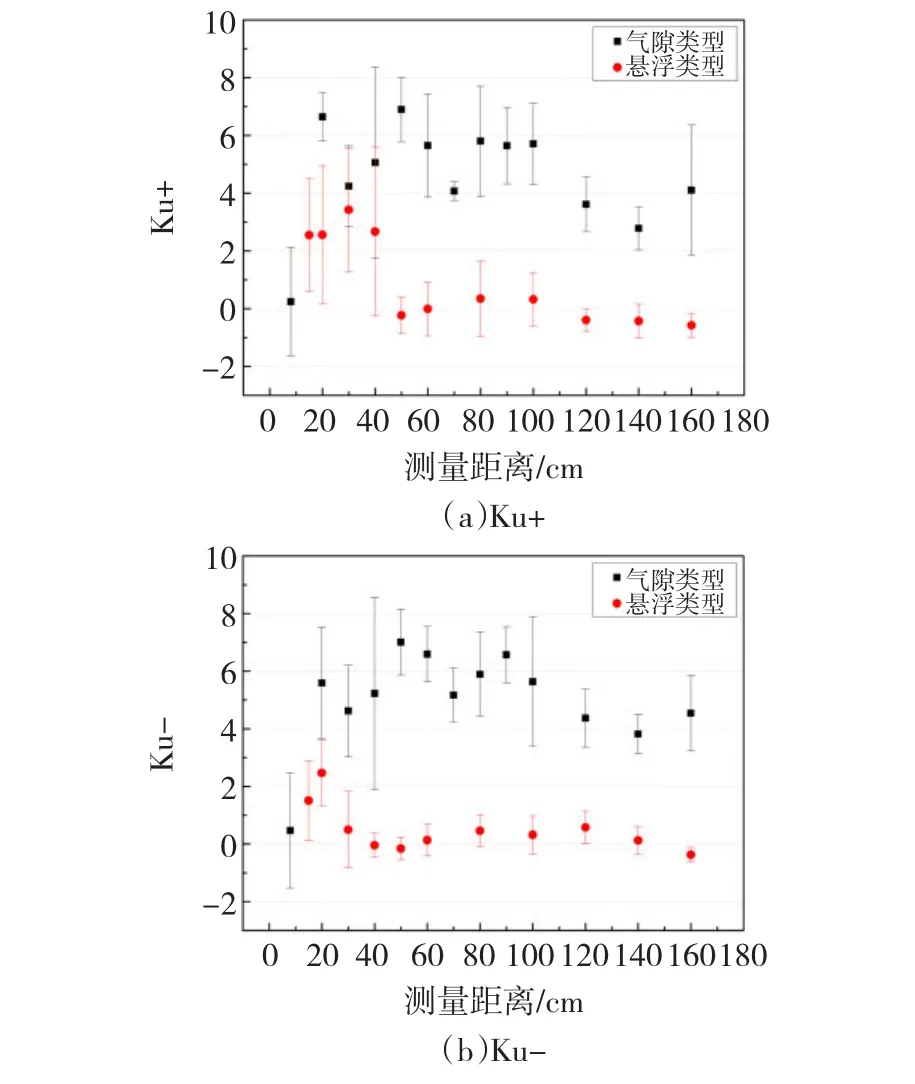
圖8 Hqmax(φ)Ku均值和方差隨檢測距離增加的變化趨勢Fig.8 The tendency of Ku in H(qmax)(φ)along with the detection distance

對于懸浮放電而言，3種譜圖(見圖8、圖9和圖10)中正負半周的峭度隨檢測距離的變化趨勢基本一致，均是隨著檢測距離增大，在50 cm處峭度值突然變小后，在50 cm至160 cm的距離內基本不變。

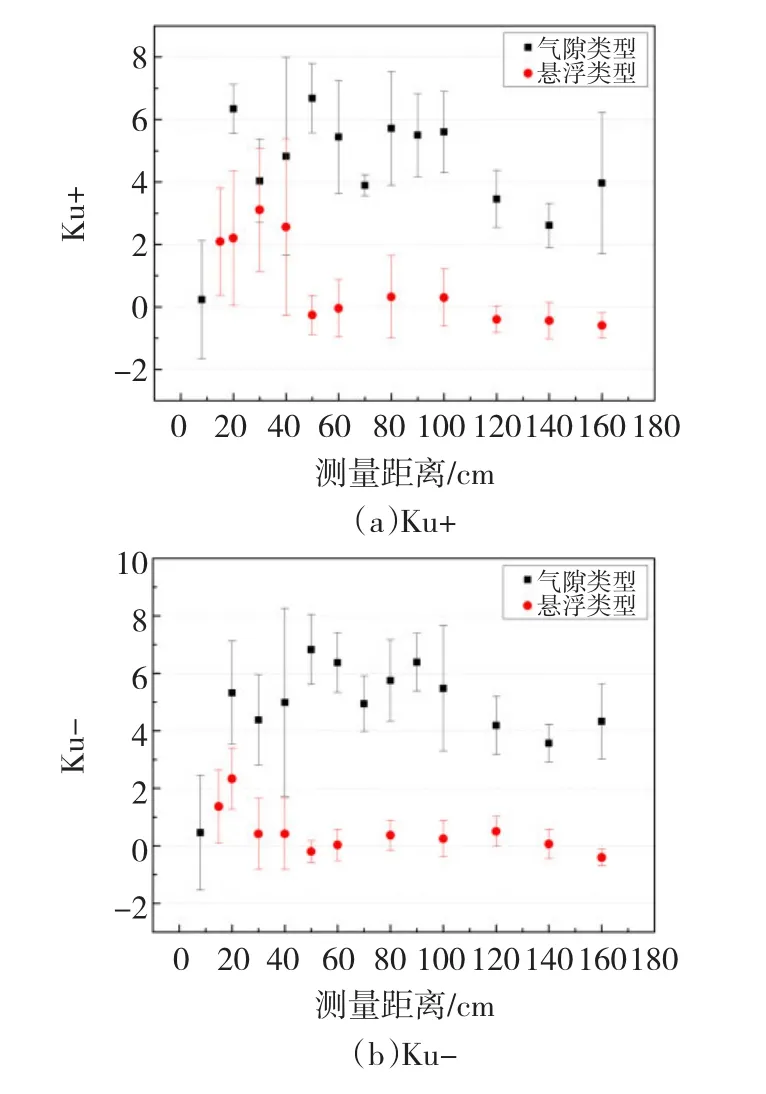
圖9 Hqn(φ)Ku均值和方差隨檢測距離增加的變化趨勢Fig.9 The tendency of Ku in H(qmax)(φ)along with the detection distance

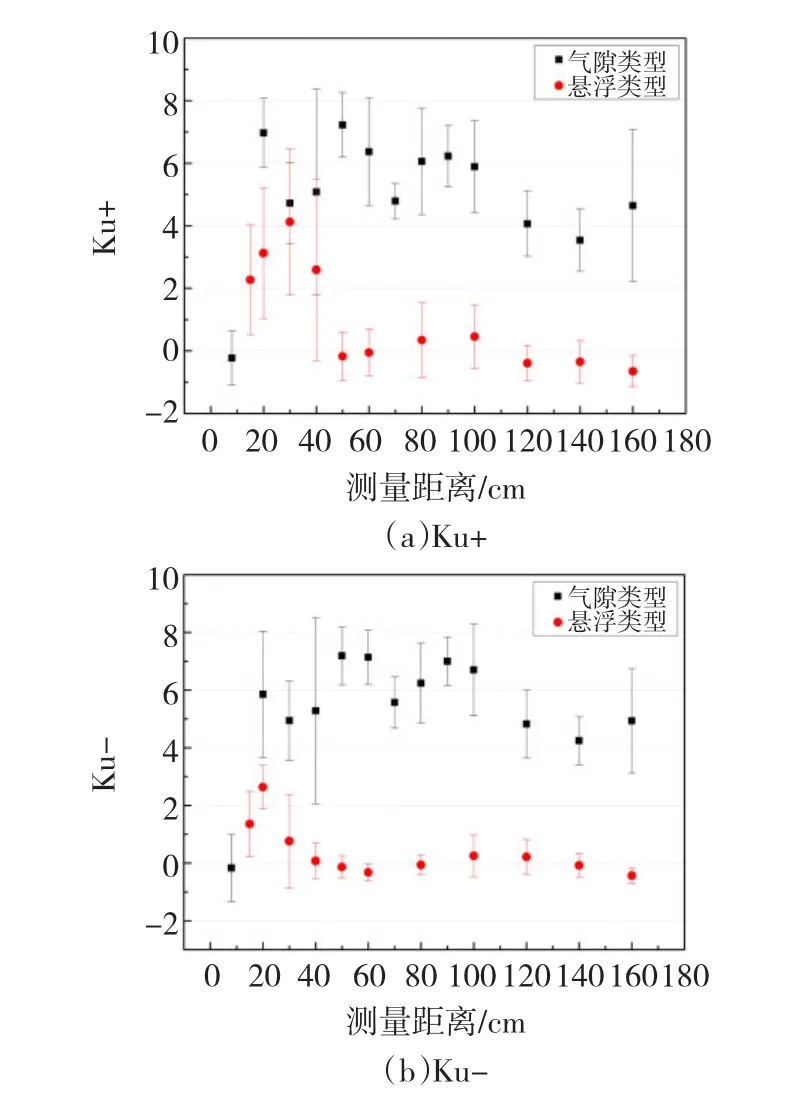
圖10 Hn(φ)Ku均值和方差隨檢測距離增加的變化趨勢Fig.10 The tendency of Ku in H(n)(φ)along with the detection distance

對比氣隙類型和懸浮類型的局部放電譜圖峭度隨檢測距離的變化趨勢，可以看出兩種放電類型的峭度值不同，且變化趨勢不同。

同樣對比上述3種譜圖，兩種放電類型的H(qmax)［n］和H(q)［n］的偏斜度值和變化趨勢基本一致，且隨著距離增加有緩慢增大的趨勢(圖11和圖12)。

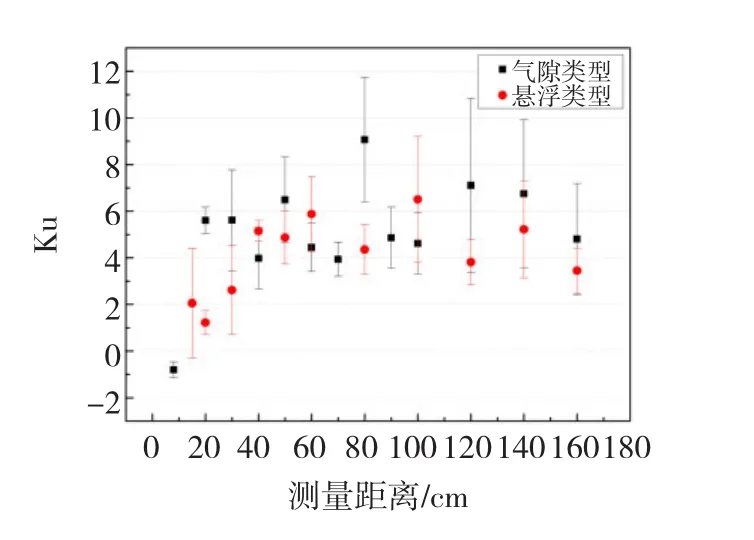
圖11 H(qmax)［n］Ku均值和方差隨檢測距離增加的變化趨勢Fig.11 The tendency of Ku in H(qmax)［n］along with the detection distance

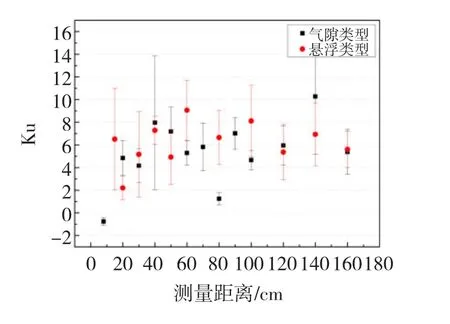
圖12 H(qn)［n］Ku均值和方差隨檢測距離增加的變化趨勢Fig.12 The tendency of Ku in H(qn)［n］along with the detection distance

2.2 .3檢測距離對相關度的影響

對于氣隙放電的3種譜圖(Hqmax(φ)、Hqn(φ)和Hn(φ))而言，當檢測距離為8 cm時，相關度基本為零，其他測量位置的相關度變化不大，基本維持在0.2～0.3之間，其次相關度的方差變化與檢測距離基本沒有關系，除40 m以外，相關度方差都比較小，說明在幾乎在所有的距離測量局部放電電磁波譜圖時相關度的波動較小。對于懸浮放電而言，隨著檢測距離增加相關度逐漸減小，在距離增加到50 cm后，相關度基本不變。對比氣隙類型和懸浮類型的局部放電譜圖相關度隨檢測距離的變化趨勢，可以看出兩種放電類型的相關度值不同，且變化趨勢在40 cm后，有一定的相似之處。綜上所述，不同放電類型特高頻局部放電譜圖的統計參量(偏斜度、峭度和相關度)隨傳播距離的增長其值的變化趨勢不相同，且在每個檢測距離處不同放電類型統計參量的數值也不相同;隨著檢測距離的增大，譜圖特征參量值隨著檢測距離的變化，在檢測距離較近時(小于20 cm)，其值與大于20 cm的值相差較大，且在大于20 cm后特征參量隨檢測距離增大存在緩慢的變化趨勢，雖然變化趨勢較為緩慢但是不同檢測距離的特征參量值存在，這為利用不同檢測距離處的特征量進行檢測距離的識別提供了依據，如圖13～圖15所示。

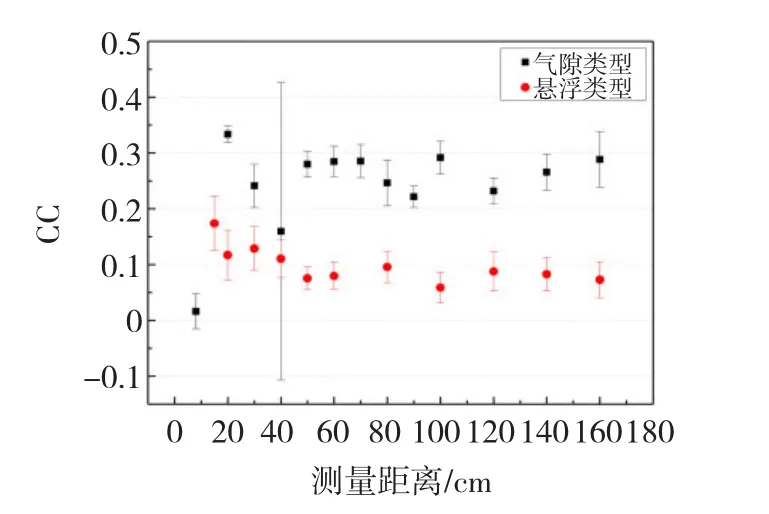
圖13 Hqmax(φ)cc均值和方差隨檢測距離增加的變化趨勢Fig.13 The tendency of cc in H(qmax)(φ)along with the detection distance

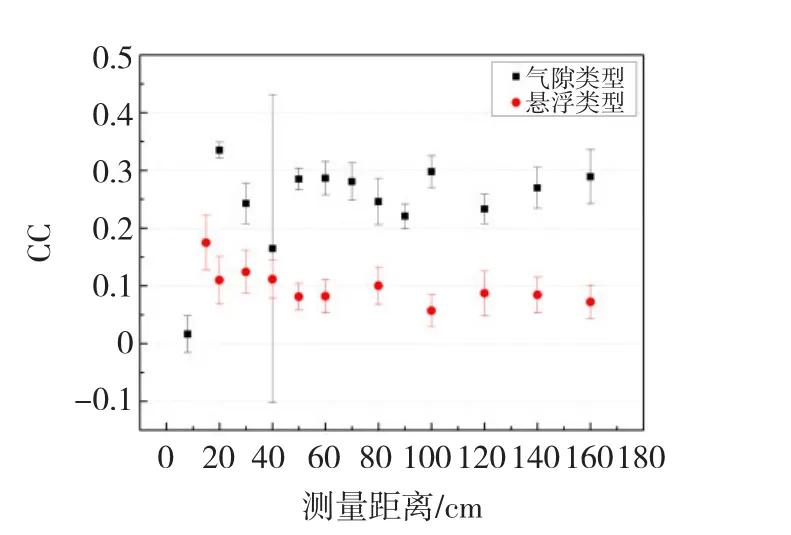
圖14 Hqn(φ)cc均值和方差隨檢測距離增加的變化趨勢Fig.14 The tendency of cc in H(qn)(φ)along with the detection distance

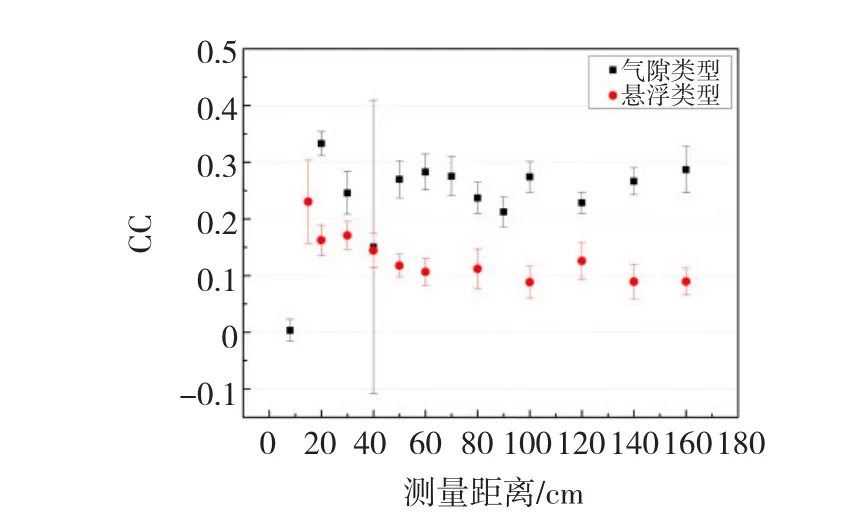
圖15 Hn(φ)cc均值和方差隨檢測距離增加的變化趨勢Fig.15 The tendency of cc in H(n)(φ)along with the detection distance

3 基于統計參量的特高頻局部放電定位

本節建立特高頻統計參量與檢測距離之間的函數關系，并通過將未知距離的特征參量代入該函數計算局部放電源距離傳感器的距離，從而實現局部放電空間定位的目的。

3.1 特高頻局部放電統計參量歸一化

由于不同的數據，量綱不同，且對于不同類型的數據其數據值相差較大，所以通常需要進行數據歸一化，歸一化是一種簡化計算的方式，即將有量綱的表達式，經過變換，化為無量綱的表達式，成為純量。比如，復數阻抗可以歸一化書寫:Z=R+jωL=R(1+jωL/R)，復數部分變成了純數，沒有量綱。另外，微波之中也就是電路分析、信號系統、電磁波傳輸等，有很多運算都可以如此處理，既保證了運算的便捷，又能凸顯出物理量的本質含義。

本文中使用的歸一化方法采用極差規范化方法，具體公式為

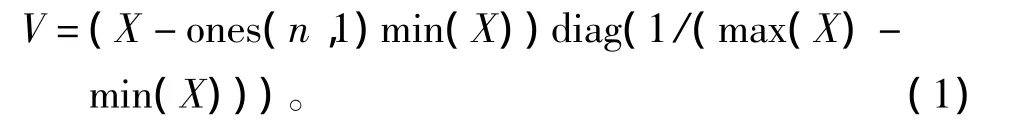
其中:x為某一個選定的特征量集合;V為該特征參量歸一化后的值。

3.2 基于多元非線性回歸的局部放電定位方法

在回歸分析中，如果有兩個或兩個以上的自變量，就稱為多元回歸。事實上，從第3節研究可以看出，多個統計參量均與檢測距離有關，故由多個特征參量的最優組合共同來預測或估計檢測距離，比只用一個特征參量進行預測或估計更有效，更符合實際。根據實驗結果，統計參量與檢測距離基本為非線性關系，故本文選用多元非線性回歸方程進行多元回歸分析，并建立多元非線性方程。同時由于不同放電類型的統計參量與檢測距離的關系不同，所以本文考慮先對兩種放電類型分別采用多元非線性回歸，建立各自的統計參量與檢測距離的多元非線性函數關系，已驗證多元非線性回歸在局部放電定位中的效果，本方法中使用的特征參量依然如表1所示。

在基于氣隙放電類型建立多元線性回歸方程后，將試驗得到的不同檢測距離下統計參量代入方程計算得到的檢測距離，除了30 cm處計算值與真實值偏差較大以外，其余均與真實值較為接近，其誤差均值為20 cm。

同理，基于懸浮類型統計參量計算得到的局部放電源距離，可以得出其計算結果與真實值也較為接近，其誤差均值為15 cm。

但是，在實際工程應用中往往并不知道放電類型，故如果針對不同的放電類型建立不同的基于統計參量的多元非線性方程，則無法確定將統計參量數據代入哪個回歸方程進行計算。

因此，本文采用了數據融合方法中最簡單直接的加權平均法對同一距離處的兩組不同類型的統計參量進行加權平均計算，其計算公式為

經過加權平均處理后，將同一檢測距離下兩種不同放電類型的統計參量融合為一組統計參量，再采用多元非線性回歸建立統計參量與檢測距離的函數關系，經實驗數據檢驗，誤差和計算結果分析見表3和圖16。從表3可以看出，對于不同檢測距離其計算誤差不同，最大誤差小于40 cm。從圖16中可以看出，其計算值與真實值之間存在一定差距，雖然不及單次放電類型的計算精度較高，但是依然可以實現比較理想的定位效果。

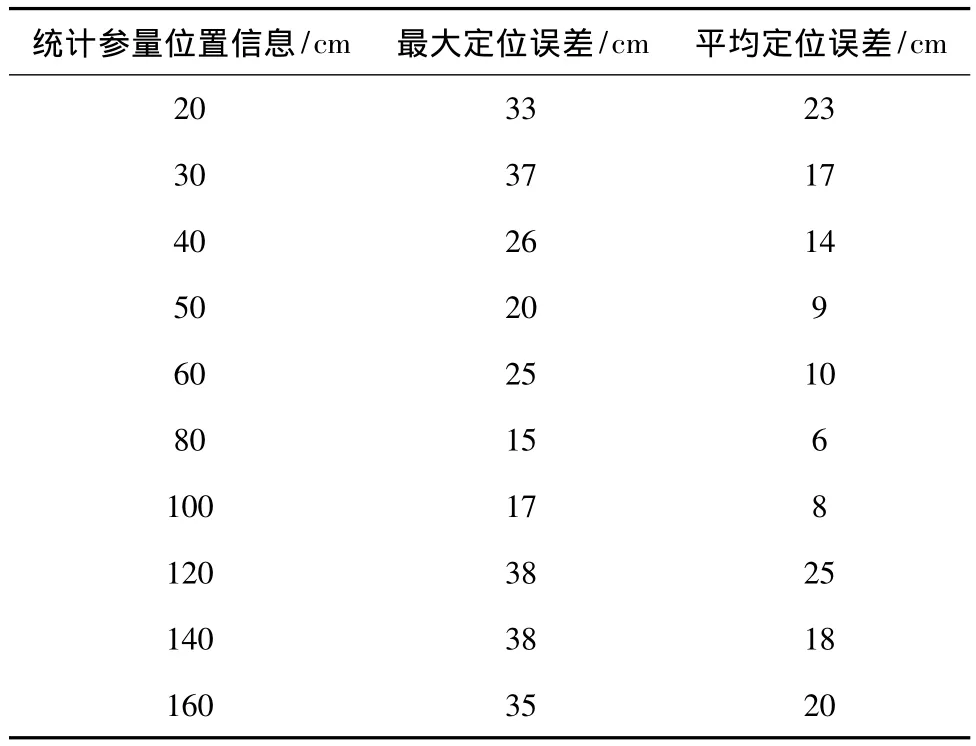
表3 局部放電定位誤差Table 3 Partial discharge location accuracy

圖16 基于氣隙和懸浮類型統計參量計算得到的局部放電源距離Fig.16 Distance from PD source to sensor based on statistic parameters of both void pattern and floating pattern

通過上述方法計算得到單個傳感器與放電源之間的距離，同時利用4個傳感器分別計算各自與放電源的距離，通過聯立放電源到各傳感器的距離公式，可以得到放電源的空間坐標范圍，從而實現放電

源的空間定位。

4 結語

通過研究局部放電特高頻信號統計參量與檢測距離的關系，引入多元非線性回歸方法建立了統計參量與檢測距離的函數關系，并通過將在任意距離處獲得的特高頻局部放電統計參量代入該函數，得到了局部放電源與傳感器間的距離，其計算結果誤差小于40 cm。

基于上述研究，提出了一種不依賴時間差的特高頻局部放電空間定位設想，如果采用多個傳感器，各個傳感器可以獨立工作，只要保證檢測信號是來自同一個放電源，那么利用多個傳感器獲得的距離信息，采用基于距離的空間定位可實現局部放電源的空間定位。

［1］JUDD MD.Evaluation of the circular metal plate as a UHF coupler for partial discharge monitoring［J］.IEE Colloquium on`Partial Discharges in Gas Insulated Substations＇，1994，93:7/1－7/47/44.

［2］JUDD MD，FARISH O，HAMPTON BF.The excitation of UHF signals by partial discharges in GIS［J］.IEEE Transactions on Dielectrics and Electrical Insulation，1996，3(2):213－228.

［3］彭超，雷清泉.局部放電超高頻信號時頻特性與傳播距離的關系［J］.高電壓技術，2013，39(2):348－353.

PENG Chao，LEI Qingquan.Relationship between characteristic in time and frequency domain of partial discharge ultra-high frequency signals and the radiation distance［J］.High Voltage Engineering，2013，39(2):213－228.

［4］常文治，唐志國，李成榕，等.變壓器局部放電UHF信號傳播特性的仿真分析［J］.高電壓技術，2009，35(7):1629－1634.

CHANG Wenzhi，TANG Zhiguo，LI Chengrong，et al.Simulation analysis of PD UHF signal propagation in transformers［J］.High Voltage Engineering，2009，35(7):1629－1634.

［5］王國利，單平，袁鵬，等.變壓器局部放電超高頻電磁波的傳播特性［J］.高電壓技術，2002，18(12):26－28.

WANG Guoli，SHAN Ping，YUAN Peng，et al.Study on the propagation characteristic of E-M wave emitted by PD in trans-formers［J］.High Voltage Engineering，2002，18(12):26－28.

［6］李劍，王小維，金卓睿，等.變壓器局部放電超高頻信號多尺度網格維數的提取與識別［J］.電網技術，2010，34(2):159－163.

LI Jian，WANG Xiaowei，JIN Zhuorui，et al.Multi-scale grid dimension extraction and recognition of ultra-high frequency signals of transformer partial discharge［J］.Power System Technology，2010，34(2):159－163.

［7］孫才新，許高峰，唐炬，等.以盒維數和信息維數為識別特征量的GIS局部放電模式識別方法［J］.中國電機工程學報，2005，25(3):100－104.

SUN Caixin，XU Gaofeng，TANG Ju，et al.PD pattern recognition method using box dimension and information dimension as discriminating features in GIS［J］.Proceedings of the CSEE，2005，25(3):100－104.

［8］張曉星，諶陽，唐俊忠，等.檢測GIS局部放電的小型準TEM

喇叭天線［J］.高電壓技術，2011，37(8):1975－1981.

ZHANG Xiaoxing，CHEN Yang，TANG Junzhong，et al.Minitype quasi－TEM horn antenna for partial discharge detection in GIS［J］.High Voltage Engineering，2011，37(8):1975－1981.

［9］唐炬，朱偉，孫才新，等.GIS局部放電的超高頻檢測［J］.高電壓技術，2003，29(12):22－23，25.

TANG Ju，ZHU Wei，SUN Caixin，et al.Analysis of UHF method used in partial discharge detection in GIS［J］.High Voltage Engineering，2003，29(12):22－23，25.

［10］趙煦，成永紅，孟永鵬，等.變壓器多參量在線監測集成系統的開發和應用［J］.中國電力，2011，44(7):31－35.

ZHAO Xu，CHENG Yonghong，MENG Yongpeng，et al.Development and application of integrated multi-parameter on-line monitoring system for power transformer［J］.Electric Power，2011，44(7):31－35.

［11］高文勝，丁登偉，劉衛東，等.采用特高頻檢測技術的局部放電源定位方法［J］.高電壓技術，2009，35(11):2680－2684.

GAO Wensheng，DING Dengwei，LIU Weidong，et al.Location of PD by searching in space using UHF method［J］.High Voltage Engineering，2009，35(11):2680－2684.

［12］侯慧娟，盛戈皞，苗培青，等.變電站局部放電特高頻信號時延的雙譜估計算法［J］.中國電機工程學報，2013(19):208－214.

HOU Huijuan，SHENG Gehao，MIAO Peiqing，et al.Time-delay estimation algorithm of partial discharge UHF signals in substation based on bispectrum［J］.Proceedings of the CSEE，2013(19):208－214.

［13］唐志國，李成榕，黃興泉，等.基于輻射電磁波檢測的電力變壓器局部放電定位研究［J］.中國電機工程學報，2006，26(3):96－101.

TANG Zhiguo，LI Chengrong，HUANG Xingquan，et al.Study of partial discharge location in power transformer based on the detection of electromagnetic waves［J］.Proceedings of the CSEE，2006，26(3):96－101.

［14］張曉星，唐炬，孫才新，等.基于多重分形維數的GIS局部放電模式識別［J］.儀器儀表學報，2007，28(4):597－602.

ZHANG Xiaoxing，TANG Ju，SUN Caixin，et al.PD pattern recognition based on multi-fractal dimensions in GIS［J］.Chinese Journal of Scientific Instrument，2007，28(4):597－602.

［15］成永紅，謝小軍，陳玉，等.氣體絕緣系統中典型缺陷的超寬頻帶放電信號的分形分析［J］.中國電機工程學報，2004，24(8):99－102.CHENG Yonghong，XIE Xiaojun，CHEN Yu，et al.Study on the fractal characteristics of ultra-wideband partial discharge in gas-insulated system(GIS)with typical defects［J］.Proceedings of the Chinese Society for Electrical Engineering，2004，24(8):99－102.

［16］成永紅，謝小軍，蔣雁，等.基于小波提取的超寬頻帶局部放電信號分形分析［J］.西安交通大學學報，2002，36(6):551－554.

CHENG Yonghong，XIE Xiaojun，JIANG Yan，et al.Study on the fractal characteristics of ultra-wideband partial discharge signals based on wavelet analysis［J］.Journal of Xi＇an Jiaotong University，2002，36(6):551－554.

［17］唐炬，孟慶紅，謝顏斌，等.采用二元樹復小波變換的GIS局放信號識別［J］.高電壓技術，2010，36(3):553－558.

TANG Ju，MENG Qinghong，XIE Yanbin，et al.Recognition of partial discharge signals in GIS using dual-tree complex wavelet transform［J］.High Voltage Engineering，2010，36(3):553－558.

［18］李立學，滕樂天，黃成軍，等.GIS局部放電超高頻信號的包絡分析與缺陷識別［J］.高電壓技術，2009，35(2):260－265.

LI Lixue，TENG Letian，HUANG Chengjun，et al.Envelope analysis and defects identification of partial discharge UHF signals in GIS［J］.High Voltage Engineering，2009，35(2):260－265.

［19］尤少華，劉云鵬，劉海峰，等.基于UHF檢測的變壓器內部典型放電實驗的譜圖分析［J］.華北電力大學學報:自然科學版，2008，35(2):18－24.

YOU Shaohua，LIU Yunpeng，LIU Haifeng，et al.Spectrogram analysis of transformer interior typical discharge based on ultrahigh frequency detection［J］.Journal of North China Electric Power University:Science and Technology，2008，35(2):18－24.

［20］GULSKI E，KREUGER F H.Computer-aided analysis of discharge patterns［J］.Journal of Physics D(Applied Physics)，1990，23(12):1569－1575.