永磁同步電機直接轉(zhuǎn)矩控制高速運行范圍拓寬

林斌， 孫丹， 賀益康

(浙江大學電氣工程學院，浙江杭州 310027)

由PMSM的轉(zhuǎn)矩和定子磁鏈公式(2)、式(3)可知，每一組(id、iq)都將對應一組(Te、ψs)，因此可得到PMSM DTC在MTPA算法下的轉(zhuǎn)矩與定子磁鏈的關系，如圖3中L1段所示。圖3為不同算法下的轉(zhuǎn)矩－定子磁鏈關系圖。可看出，MTPA運行階段轉(zhuǎn)矩隨定子磁鏈的增大而增大。

點A是MTPA曲線與電流限制圓的交點，若在該點上運行，PMSM可在保持定子電流為最大值條件下輸出最大轉(zhuǎn)矩。將式(11)中Is取值為Imax，可得A點所對應的電流、轉(zhuǎn)矩、定子磁鏈為

0 引言

直接轉(zhuǎn)矩控制(direct torque control，DTC)在定子坐標系中實施運算，無需坐標旋轉(zhuǎn)變換及轉(zhuǎn)子位置信息，具有結(jié)構(gòu)簡單，轉(zhuǎn)矩動態(tài)響應快，參數(shù)魯棒性強等諸多優(yōu)點，作為一種高性能的交流電機控制策略，其研究得到了學術界和工業(yè)界的廣泛關注［1－6］。

然而基于開關表和滯環(huán)控制器的常規(guī)DTC方式，存在轉(zhuǎn)矩波動大、開關頻率不固定等缺點［1］。已有大量文獻對其進行了改進研究，提高了系統(tǒng)穩(wěn)態(tài)精確度［2－6］。其中文獻［2－3］將空間電壓調(diào)制(space vector modulation，SVM)方法引入永磁同步電機(permanent magnet synchronous motor，PMSM)常規(guī)DTC中，雖系統(tǒng)復雜度略有增加，但實現(xiàn)了開關頻率固定，極大提高了系統(tǒng)穩(wěn)態(tài)精確度，也保持了快速的動態(tài)響應性能，被廣泛認可。但對于PMSM的大量DTC改進研究都是在基速以下，較少涉及弱磁高速運行。

DTC方式下PMSM的弱磁高速運行理論源自矢量控制(vector control，VC)下的弱磁運行。PMSM弱磁高速運行時應滿足電壓和電流的限制，有文獻分別討論了在該限制條件下PMSM基于VC的最大轉(zhuǎn)矩電流比(maximum torque per ampere，MTPA)［7］、恒 功 率 轉(zhuǎn) 速 比(constant power speed range，CPSR)［8］、最大轉(zhuǎn)矩電壓比(maximum torque per voltage，MTPV)［8］等3種運行方式，以期實現(xiàn)最大轉(zhuǎn)矩及高速的運行目標。VC是通過對定子電流矢量的交、直軸分量進行獨立(解耦)控制而實現(xiàn)的，DTC則是通過對轉(zhuǎn)矩和定子磁鏈的控制來實現(xiàn)的。由于PMSM的轉(zhuǎn)矩、定子磁鏈與交、直軸電流分量有相互對應關系，據(jù)此文獻［9］討論了基于DTC的MTPA和CPSR弱磁方法。也有文獻指出在電流限制條件下PMSM DTC弱磁運行時，如轉(zhuǎn)矩角超過最大允許值，可能會導致電機運行失步，無法實現(xiàn)PMSM的高速穩(wěn)定運行［9－10］。

按照VC方式直接推得的DTC弱磁控制算法在轉(zhuǎn)矩和定子磁鏈計算時需用到交、直軸電感和永磁體磁鏈，對電機參數(shù)的依賴很大。因而需探求一種結(jié)構(gòu)簡便、參數(shù)魯棒性更好的控制方法。文獻［11－12］提出了一種新穎的電磁轉(zhuǎn)矩給定值的計算方法，但需用到三相靜止坐標系到兩相旋轉(zhuǎn)坐標系的旋轉(zhuǎn)變換，計算量較大。

為解決DTC方式下PMSM的運行穩(wěn)定性問題，本文將首先系統(tǒng)地分析MTPA、CPSR和MTPV 3種算法下PMSM的運行狀態(tài)，指出高速穩(wěn)定運行的關鍵。其次在常規(guī)SVM－DTC策略的基礎上，提出一種轉(zhuǎn)矩角限幅方法，以拓寬電機穩(wěn)定運行的速度范圍。進一步還提出一種利用定子磁鏈和電流的轉(zhuǎn)矩給定值計算方法，確保了PMSM DTC的高速穩(wěn)定運行，有效提高了系統(tǒng)魯棒性，并使電機穩(wěn)定運行不再受轉(zhuǎn)矩角的影響。詳盡的仿真研究結(jié)果驗證了DTC方式下PMSM的兩種拓寬高速穩(wěn)定運行區(qū)域的方法的可行性和有效性。

1 PMSM的運行階段及轉(zhuǎn)矩角分析

PMSM在不同坐標系下的矢量圖如圖1所示。在轉(zhuǎn)子磁鏈定向的d-q同步旋轉(zhuǎn)坐標系下，PMSM的電壓、定子磁鏈、電磁轉(zhuǎn)矩方程可分別表示為

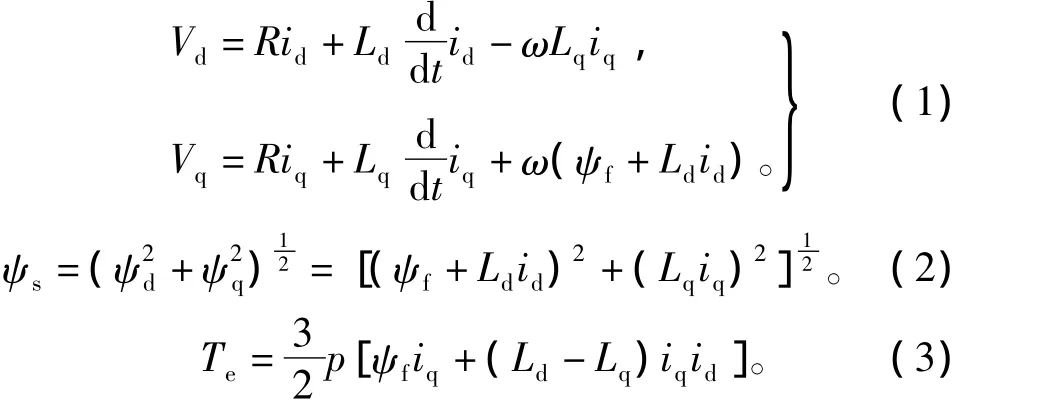
其中:Vd、Vq、id、iq、Ld、Lq、ψd、ψq分別是d、q軸電壓、電流、電感和定子磁鏈;ψs、ψf分別是定、轉(zhuǎn)子磁鏈;Te是電機的電磁轉(zhuǎn)矩;R是定子繞組的電阻;ω是轉(zhuǎn)子的電角速度，即d-q坐標系的旋轉(zhuǎn)角速度;p是電機的極對數(shù)。

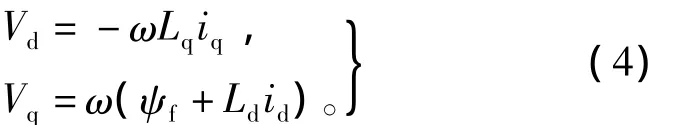
由逆變器驅(qū)動運行的永磁同步電機存在電流和電壓的極限約束條件，即有電流和電壓極限方程為

其中:Imax為允許的最大定子電流;Vmax為允許的最大定子電壓，一般由逆變器直流母線電壓Vdc決定，即Vmax=Vdc/。

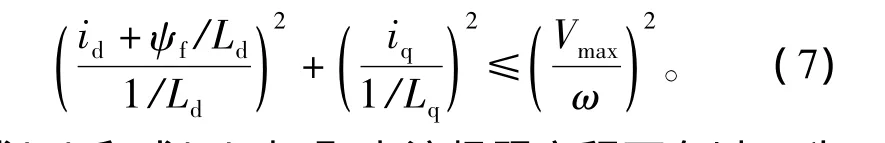
式(5)和式(7)表明，電流極限方程可在以id為X軸，iq為Y軸的坐標系內(nèi)形成一個以O1(0，0)為圓心、Imax為半徑的圓;電壓極限方程也可畫成一個以O2(－ψf/Ld，0)為圓心、長短軸與Vmax/ω成正比的橢圓;上述電流限制圓和電壓極限圓如圖2中所示。隨著轉(zhuǎn)速ω的升高，電壓極限圓與轉(zhuǎn)速成反比變小。需要說明的是，文中所繪圖形均依據(jù)下文仿真研究中的嵌入式PMSM參數(shù)所得［1］，此類PMSM的特征是電壓限制圓的圓心位于電流限制圓之內(nèi)。

將式(4)帶入式(6)，可得

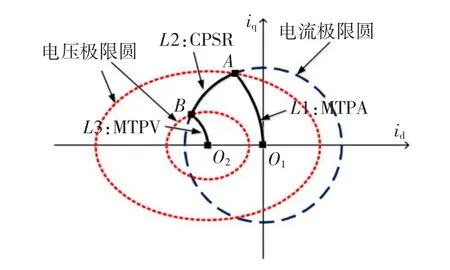
圖2 電流電壓限制圓與運行軌跡Fig.2 The limit circles of current and voltage and the operation loci

在對PMSM進行控制時，需確保id、iq值在電流和電壓限制圓內(nèi)。當電機轉(zhuǎn)速低于基速時，電壓限制圓的半徑較大，id、iq的取值只需滿足電流限制圓的要求，此時通常采用MTPA［7］算法，確保單位電流下輸出最大轉(zhuǎn)矩，其運行軌跡如圖2中L1段所示。當電機運行于基速以上時，電機端電壓達到極限，為保證在同時滿足電流和電壓限幅的條件下電機加速運行，則其運行軌跡必須沿電流限制圓逆時針方向運動，即采用CPSR［8］算法，如圖2中L2段所示。由式(2)可知，如id反向增大可減弱d軸磁鏈，同時id幅值的增大也可導致iq減小，使得定子磁鏈的幅值減小，以弱磁的方式來滿足電壓極限條件。當電機運行于更高轉(zhuǎn)速時，為獲得單位電壓下的最大轉(zhuǎn)矩輸出，可采用MTPV［8］算法，即沿著電壓極限圓縮小的軌跡運行，如圖2中L3段所示。可看出，CPSR階段能同時利用電壓和電流的最大極限容量，而MTPV階段電流并非維持在其極限值，但MTPV階段的輸出轉(zhuǎn)矩將大于CPSR階段，對此后文將予以證明。

為保證PMSM DTC系統(tǒng)的穩(wěn)定運行，必須考察其轉(zhuǎn)矩角的變化情況，因此需對PMSM DTC的MTPA、CPSR和MTPV運行方式進行討論，并對各階段的轉(zhuǎn)矩角情況進行深入分析。

1.1 MTPA

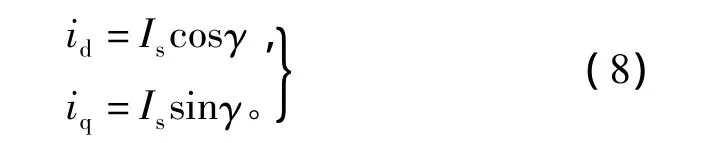
設電流矢量Is與d軸的夾角為γ，有其中，Is為電流矢量Is的幅值。則電磁轉(zhuǎn)矩方程可改寫為

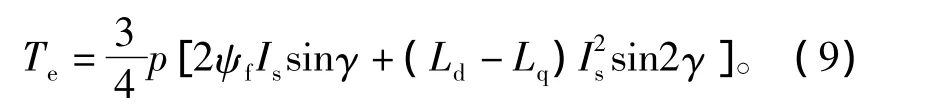
在電流極限約束條件下，要求單位電流輸出最大轉(zhuǎn)矩，可對式(9)求導并整理可得

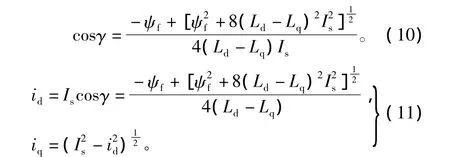
由PMSM的轉(zhuǎn)矩和定子磁鏈公式(2)、式(3)可知，每一組(id、iq)都將對應一組(Te、ψs)，因此可得到PMSM DTC在MTPA算法下的轉(zhuǎn)矩與定子磁鏈的關系，如圖3中L1段所示。圖3為不同算法下的轉(zhuǎn)矩－定子磁鏈關系圖。可看出，MTPA運行階段轉(zhuǎn)矩隨定子磁鏈的增大而增大。

點A是MTPA曲線與電流限制圓的交點，若在該點上運行，PMSM可在保持定子電流為最大值條件下輸出最大轉(zhuǎn)矩。將式(11)中Is取值為Imax，可得A點所對應的電流、轉(zhuǎn)矩、定子磁鏈為

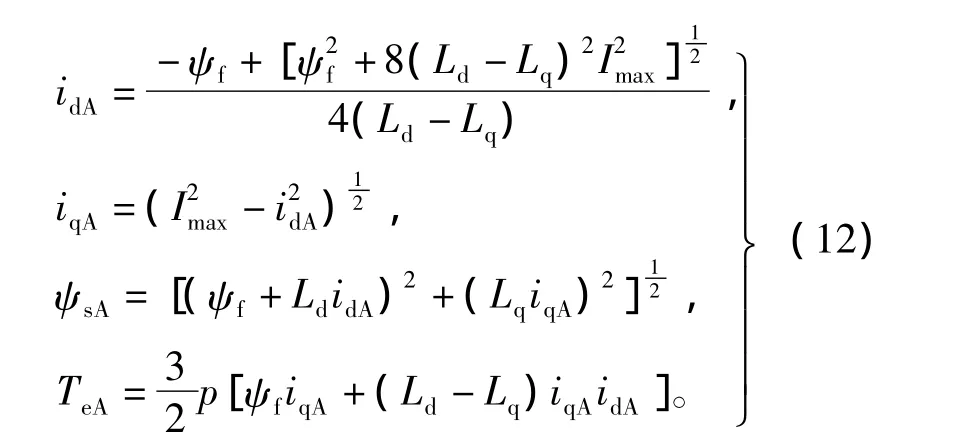
由電壓極限方程可知，電壓極限圓隨著轉(zhuǎn)速的增大而變小。當轉(zhuǎn)速ω小于基速ωb時，電機運行僅需考慮電流限制圓，在A點運行滿足電流限制條件，并可輸出最大轉(zhuǎn)矩。而當ω增大，電壓限制圓逐漸變小將與電流限制圓交于A點，此時需同時考慮電流與電壓的限制要求。

1.2 CPSR

當轉(zhuǎn)速上升到基速ωb、定子端電壓也達到最大值Vmax，id、iq的取值必須同時滿足電壓和電流極限條件。將式(5)和式(7)2個不等式取等號求解可得

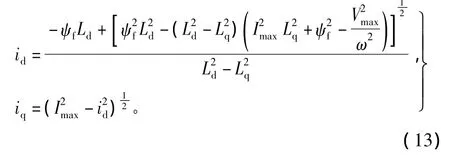
同理，根據(jù)式(2)、式(3)可得CPSR算法下的轉(zhuǎn)矩與定子磁鏈的關系，如圖3中L2段所示，圖中ω2＞ω1＞ωb。可看出，轉(zhuǎn)矩和定子磁鏈均隨著轉(zhuǎn)速的提高而減小，符合弱磁運行時的電機特性。

1.3 MTPV

當電機超過某一轉(zhuǎn)速后，任一給定轉(zhuǎn)速下，電動機電壓極限圓軌跡上存在著一輸出轉(zhuǎn)矩最大的點。

根據(jù)式(7)，可得

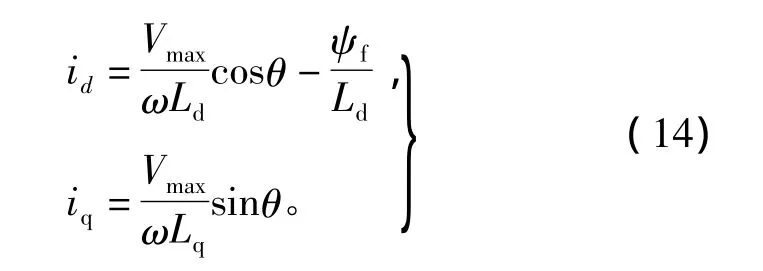
其中，θ為一角度變量。

則電磁轉(zhuǎn)矩可改寫為

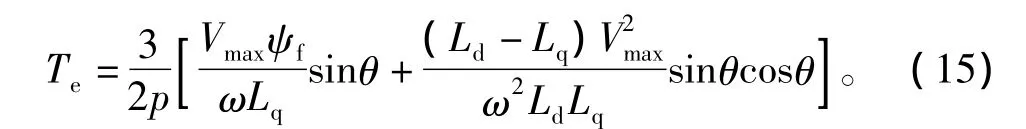
對式(15)求導，并整理可得

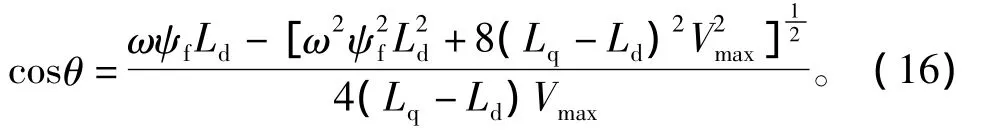
令cosθ=λ，則有

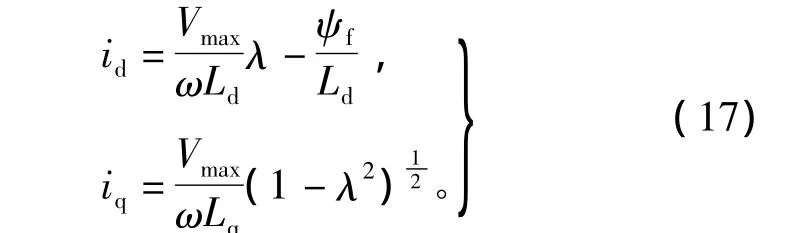
同理，由式(2)、式(3)可得MTPV算法下的轉(zhuǎn)矩與定子磁鏈的關系，如圖3中L3段所示。

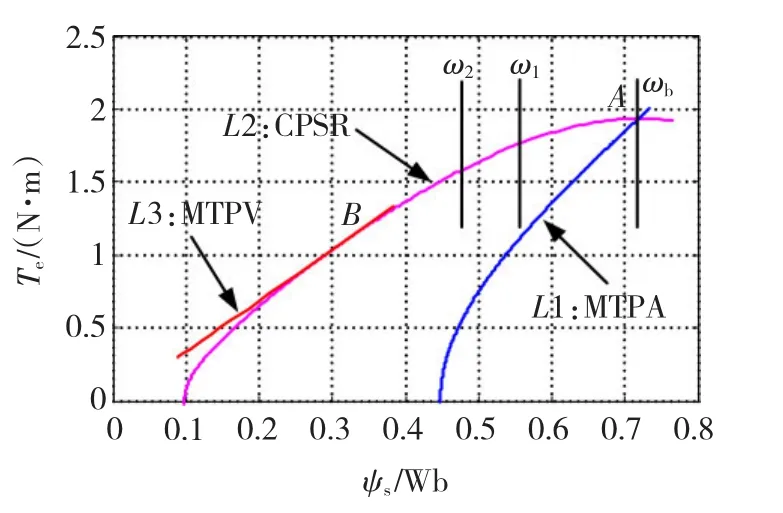
圖3 轉(zhuǎn)矩－定子磁鏈關系圖Fig.3 Relationship between torque and stator flux linkage

可看出圖3中的L3段與L2段相交于B點，即MTPV曲線與電流限制圓的交點，與圖2對應。可發(fā)現(xiàn)在相同的定子磁鏈條件下L3段的轉(zhuǎn)矩大于L2段，說明如在B點之后選擇MTPV算法，則可在滿足電壓電流限制條件下輸出更大的轉(zhuǎn)矩。

1.4 轉(zhuǎn)矩角

PMSM電磁轉(zhuǎn)矩方程可用定、轉(zhuǎn)子磁鏈的關系表示為

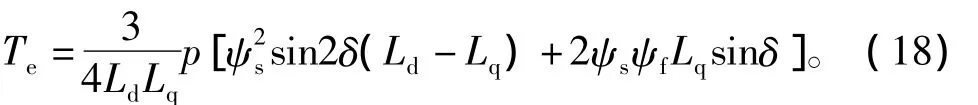
其中，δ為轉(zhuǎn)矩角，即定、轉(zhuǎn)子磁鏈矢量間的夾角。對式(18)求導得

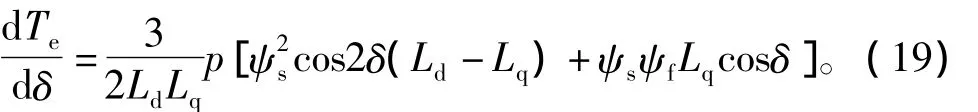
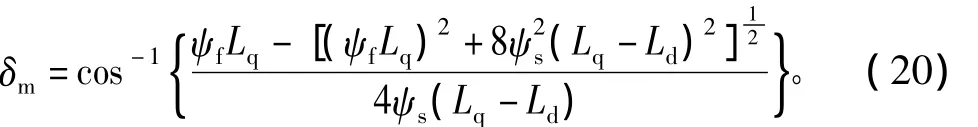
在PMSM DTC系統(tǒng)中，當δ＜δm時轉(zhuǎn)矩值將隨轉(zhuǎn)矩角的增大而增大，當δ=δm時轉(zhuǎn)矩達最大;而當δ＞δm時轉(zhuǎn)矩值將隨著δ的增大而減小，最終將會導致轉(zhuǎn)矩關系不平衡而使電機運行失步。因此弱磁控制時為保證系統(tǒng)運行穩(wěn)定必須保持δ≤δm。

根據(jù)式(18)可知，Te、ψs、δ 3者中只有2個獨立，因此在已知MTPA－CPSR－MTPV 3個階段中Te隨ψs變化軌跡的前提下，可繪制出δ隨ψs變化的軌跡，如圖4所示。圖中L1段為MTPA，L2段為CPSR，L3段為MTPV。同時由式(20)還可得到最大轉(zhuǎn)矩角δm隨ψs變化的關系，如圖4中L4段所示。

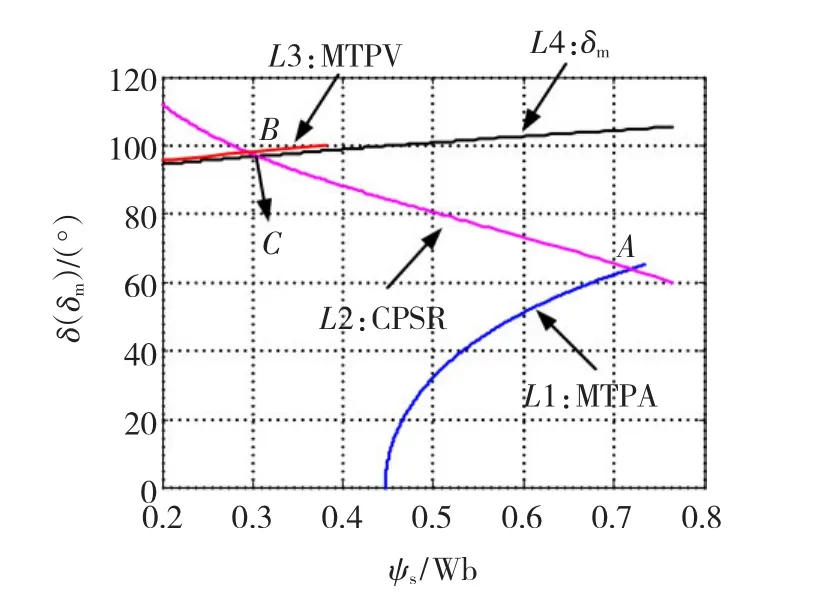
圖4 轉(zhuǎn)矩角(最大轉(zhuǎn)矩角)－定子磁錠關系圖Fig.4 Relationship between torque angle(maximum torque angle)and stator flux linkage

由圖4可知，在整個MTPA階段δ均小于δm;在CPSR階段隨著轉(zhuǎn)速的不斷上升ψs逐漸減小，δ隨之增大，而 δm隨之減小。在 ψs=0.306 Wb，δm=96.97°的C點，δ等于 δm，C點之后 δ超過 δm導致CPSR運行區(qū)域出現(xiàn)不穩(wěn)定。而在MTPV整個階段的轉(zhuǎn)矩角δ始終大于最大轉(zhuǎn)矩角δm，無法穩(wěn)定運行。因此為了使PMSM DTC系統(tǒng)速度運行范圍得到拓展，必須進行必要的改進。

2 PMSM SVM-DTC弱磁運行的實現(xiàn)

傳統(tǒng)PMSM SVM－DTC的結(jié)構(gòu)框圖如圖5所示［2］。其中，轉(zhuǎn)矩與定子磁鏈給定值計算模塊如圖6所示。當ω ＜ωb，輸出轉(zhuǎn)矩最大值為圖3中A點所對應的轉(zhuǎn)矩。而當ω＞ωb之后，受制于電壓極限，轉(zhuǎn)矩將無法維持該最大值。根據(jù)圖3，CPSR運行階段每一轉(zhuǎn)速將對應一個最大輸出轉(zhuǎn)矩，且其值隨轉(zhuǎn)速的升高而降低。據(jù)此可制定出一個最大轉(zhuǎn)矩－轉(zhuǎn)速查詢表Temax=f(ω)，以對通過轉(zhuǎn)速PI調(diào)節(jié)器獲得的初始轉(zhuǎn)矩給定T'e實現(xiàn)限幅，獲得最終的轉(zhuǎn)矩給定值。

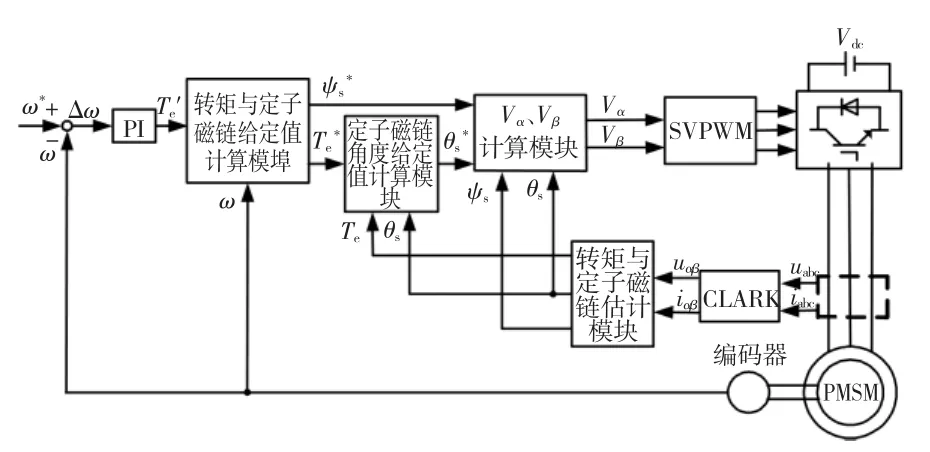
圖5 傳統(tǒng)永磁同步電機直接轉(zhuǎn)矩控制結(jié)構(gòu)框圖Fig.5 Block diagram of SVM DTC for PMSM

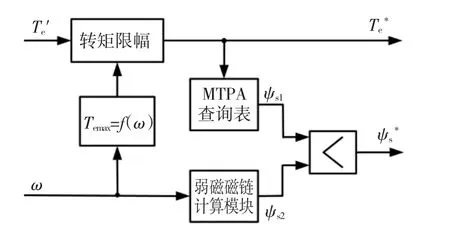
圖6 轉(zhuǎn)矩與定子磁鏈給定值計算模塊Fig.6 Calculator of reference torque andstator flux linkage

當ω＜ωb時電機按MTPA軌跡運行，此時可根據(jù)轉(zhuǎn)矩與定子磁鏈的對應關系，通過查詢MTPA表格獲得轉(zhuǎn)矩給定下所對應的定子磁鏈ψs1。而當ω＞ ωb之后為滿足電壓極限要求，根據(jù)ψs2=Umax/ω關系，定子磁鏈需隨轉(zhuǎn)速的增大而減小。通常在低速時ψs1小于ψs2，高速時ψs1大于ψs2，此時可通過對ψs1和ψs2的比較，取小值作為定子磁鏈的實際給定幅值。

由式(18)可知，在定子磁鏈幅值一定的情況下電磁轉(zhuǎn)矩主要由轉(zhuǎn)矩角來決定。因此可利用PI調(diào)節(jié)器將轉(zhuǎn)矩的誤差反映到轉(zhuǎn)矩角的變化上，繼而通過改變定子磁鏈相對于α軸的夾角來改變參考電壓空間矢量的給定值，實現(xiàn)對轉(zhuǎn)矩的有效控制。圖7即為定子磁鏈角度給定值計算模塊。

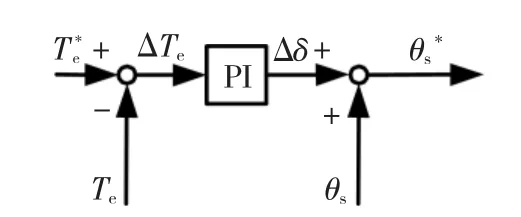
圖7 定子磁鏈角度給定值計算模塊Fig.7 Calculator of reference stator flux linkage angle

3 轉(zhuǎn)矩角限幅方法

在基速以上，隨著轉(zhuǎn)速的上升定子磁鏈減小，由圖4可見，最大轉(zhuǎn)矩角也變小;但按CPSR算法求得的轉(zhuǎn)矩角卻隨轉(zhuǎn)速增加而增大。為了保證作為DTC穩(wěn)定運行依據(jù)的PMSM轉(zhuǎn)矩角和轉(zhuǎn)矩之間的正比例關系，滿足δ≤δm的穩(wěn)定運行條件，必須對轉(zhuǎn)矩角實施限幅。通過對圖5的觀察發(fā)現(xiàn)，MTPV階段的δ略大于δm且與δm非常接近，因此可以在C點之后通過對δ進行限幅而實現(xiàn)類MTPA算法下的高速運行。考慮到傳統(tǒng)PMSM SVM－DTC中沒有對轉(zhuǎn)矩角進行直接觀測和控制，必須對算法進行改進。

由圖4可知，最大轉(zhuǎn)矩角δm與定子磁鏈ψs間存在一一對應關系;而在弱磁階段定子磁鏈ψs與轉(zhuǎn)速ω間同樣存在對應關系，因此可得到以查詢表表示的最大轉(zhuǎn)矩角與轉(zhuǎn)速之間的關系δm=f(ω)，這樣就可根據(jù)轉(zhuǎn)速ω來確定允許的最大轉(zhuǎn)矩角δm，實現(xiàn)δ限幅控制。

圖8為基于轉(zhuǎn)矩角限幅的定子磁鏈角度給定值計算框圖。在通過傳統(tǒng)算法得到定子磁鏈矢量初始給定相對于α軸的夾角θ's后，與電機轉(zhuǎn)速ω積分求得的轉(zhuǎn)子位置角θe比較，得到給定轉(zhuǎn)矩角δ。再通過查表得到允許最大轉(zhuǎn)矩角δm，實現(xiàn)對給定轉(zhuǎn)矩角限幅，按此從轉(zhuǎn)矩的限制角度保證滿足穩(wěn)定運行條件。最后將經(jīng)限幅后的給定轉(zhuǎn)矩角與轉(zhuǎn)子位置角θe相加，即可作為給定定子磁鏈相對于α軸的夾角給定值。

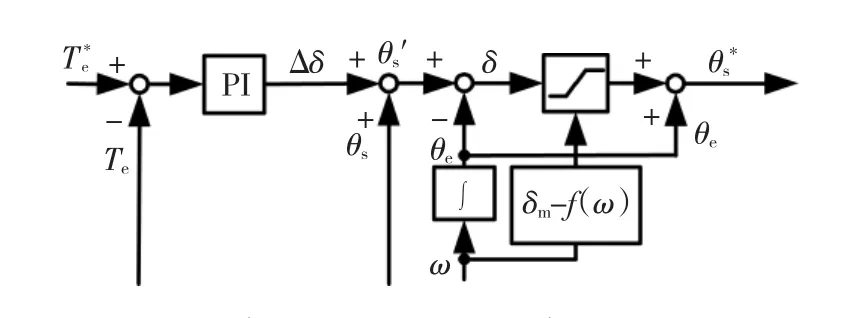
圖8 基于轉(zhuǎn)矩角限幅的定子磁鏈角度給定值計算框圖Fig.8 Calculation diagram of reference stator flux linkage angle based on torque angle limitation

上述分析表明，通過轉(zhuǎn)矩角限幅之后的PMSM SVM－DTC可在高速時達到類MTPV的運行效果。可見該改進方法的優(yōu)勢是能在不過多增加運算復雜性的前提下，通過對電機轉(zhuǎn)矩角的有效處理，保證電機的高速穩(wěn)定運行，同時實現(xiàn)了最大轉(zhuǎn)矩輸出。但其運行特征與MTPV算法相似，即在轉(zhuǎn)速逐漸上升時保持電機端電壓最大，電流幅值隨之減小。

4 改進給定轉(zhuǎn)矩計算方法

在傳統(tǒng)PMSM的SVM－DTC弱磁運行中，轉(zhuǎn)矩限幅值是根據(jù)Temax=f(ω)關系通過查表獲得，而該表的建立對交、直軸電感Ld、Lq和永磁體磁鏈ψf等電機參數(shù)的依賴較大，系統(tǒng)魯棒性較差。同樣，基于轉(zhuǎn)矩角限幅的改進策略中也需要用到Temax=f(ω)關系，同樣也需依賴精確的電機參數(shù)。對此本文進一步提出一種基于定子磁鏈定向、對電機參數(shù)依賴性小的改進轉(zhuǎn)矩給定方法，其算法如圖9所示。

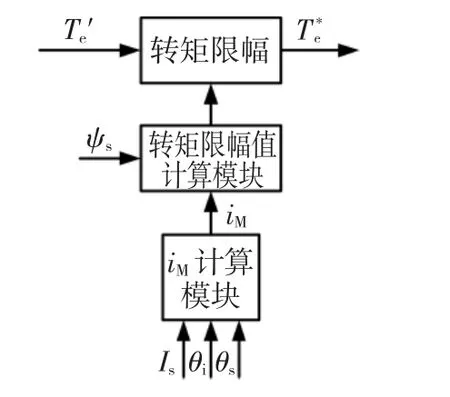
圖9 給定轉(zhuǎn)矩改進方法Fig.9 Modified algorithm of reference torque

定子磁鏈定向即將同步速旋轉(zhuǎn)的M－T坐標系的M軸定在定子磁鏈矢量方向上，如圖1中所示。此時有定子磁鏈M軸分量ψM=ψs，T軸分量ψT=0。

這樣定子磁鏈定向下電磁轉(zhuǎn)矩方程可表示為

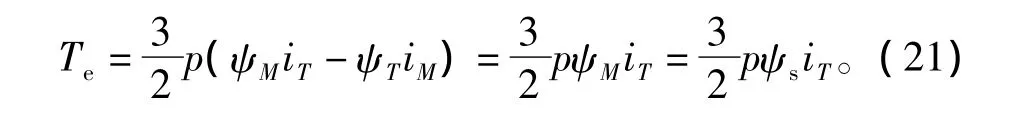
其中，iM、iT分別為定子電流的M軸和T軸分量。

在M－T坐標系下，轉(zhuǎn)矩限幅值可表示為

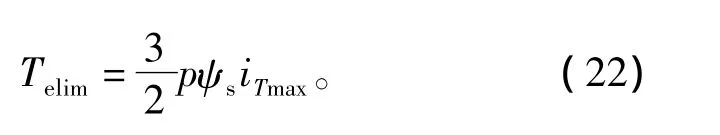
其中，iTmax為下式計算得T軸電流的最大值，可表示為

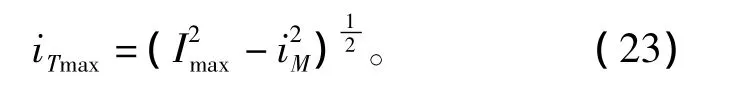
其中，定子電流M軸分量iM為

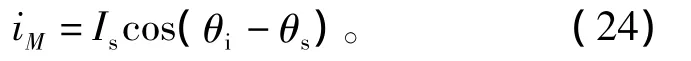
其中:θi為定子電流矢量Is相對于α軸的夾角;θs為定子磁鏈矢量ψs相對于α軸的夾角，如圖1所示。

利用轉(zhuǎn)矩限幅值Telim對轉(zhuǎn)速PI調(diào)節(jié)器的輸出T'e實施限幅，即可得到改進的給定轉(zhuǎn)矩T*e。

上述改進轉(zhuǎn)矩給定算法，利用定子磁鏈與定子電流在定子磁場方向上分量的乘積獲得轉(zhuǎn)矩限幅值，能夠?qū)崟r地根據(jù)系統(tǒng)的實際運行狀態(tài)計算轉(zhuǎn)矩限幅值，不再需要保持轉(zhuǎn)矩角和轉(zhuǎn)矩之間的嚴格正比例的關系，因此轉(zhuǎn)矩角無需維持在最大轉(zhuǎn)矩角范圍內(nèi)，就可實現(xiàn)高速穩(wěn)定運行。而且由于改進算法中轉(zhuǎn)矩限幅值與交、直軸電感和轉(zhuǎn)子永磁體磁鏈沒有直接聯(lián)系，因此對電機參數(shù)依賴小，魯棒性強。

5 仿真研究

為驗證上述分析和改進方法的正確性，針對一內(nèi)嵌式PMSM進行了基于Matlab/SIMULINK的仿真研究，電機參數(shù)如下:極對數(shù)為2，定子電壓18.6 Ω，直軸電感0.388 5 H，交軸電感0.475 5 H，永磁磁鏈0.447 Wb，最大定子電壓240 V，最大定子電流1.4 A，額定轉(zhuǎn)矩1.94 N·m。運行條件為空載啟動至轉(zhuǎn)速6 000 r/min，。圖10～圖12分別是PMSM基于傳統(tǒng)SVM－DTC、轉(zhuǎn)矩角限幅SVM－DTC和給定轉(zhuǎn)矩改進SVM－DTC的運行特性。

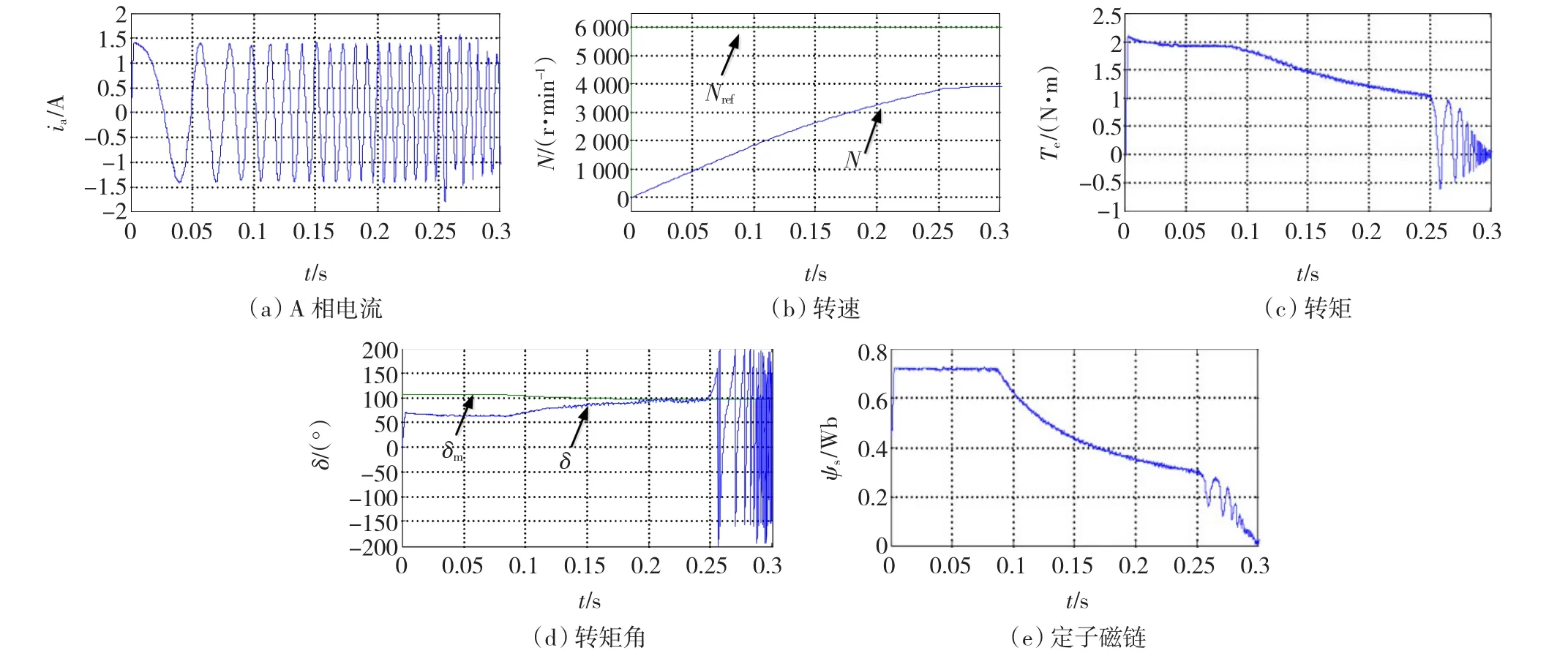
圖10 傳統(tǒng)PMSM SVM-DTCFig.10 Conventional PMSM SVM-DTC

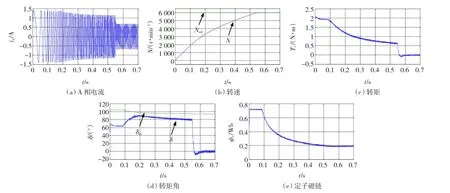
圖11 轉(zhuǎn)矩角限幅PMSM SVM-DTCFig.11 PMSM SVM-DTC based on torque angle limitation

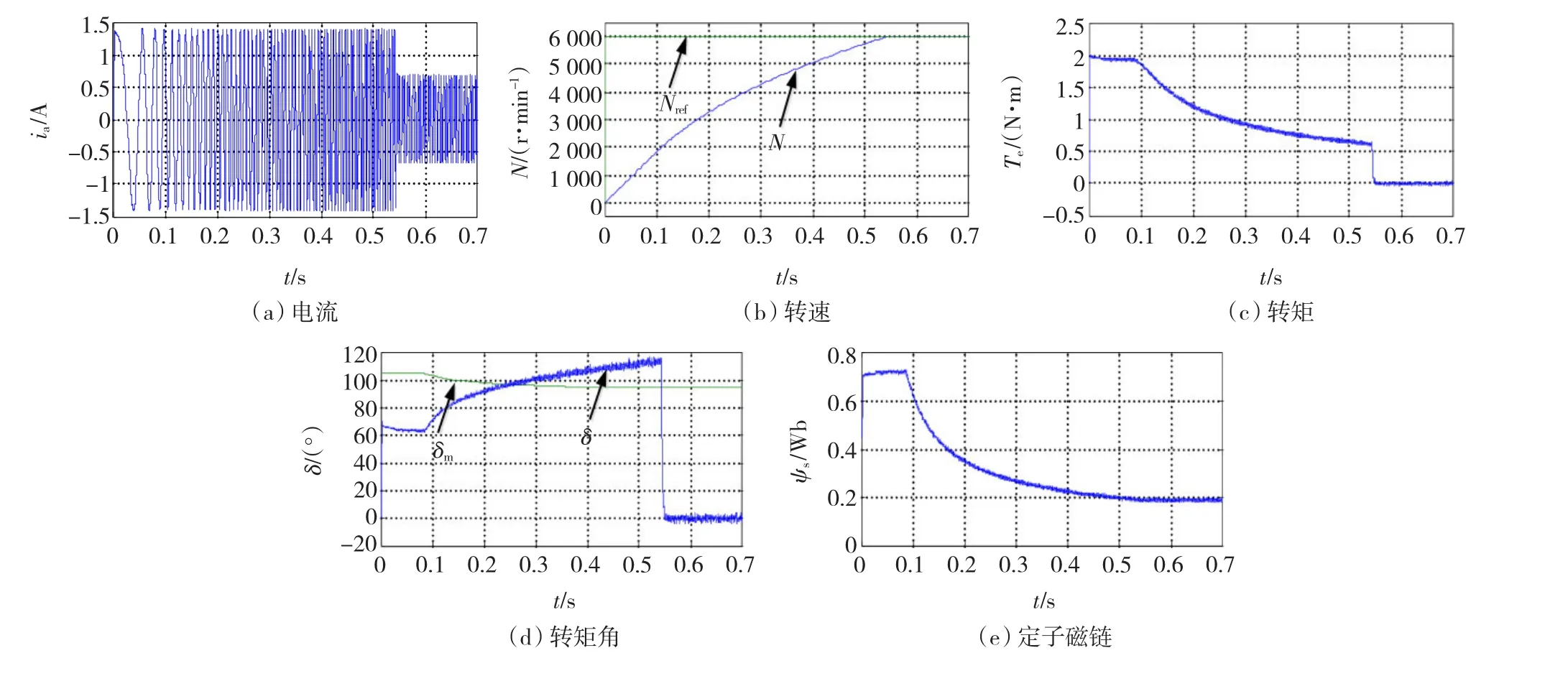
圖12 給定轉(zhuǎn)矩改進PMSM SVM-DTC Fig.12 PMSM SVM-DTC based on modified reference torque algorithm

由圖10可知，在t=0.25 s之前，基于傳統(tǒng)SVMDTC的PMSM運行穩(wěn)定，電流保持最大幅值，轉(zhuǎn)速平穩(wěn)升高。升速過程中轉(zhuǎn)矩角一直小于最大轉(zhuǎn)矩角，基速以上磁鏈開始變小。在t=0.25 s之后電流開始波動，轉(zhuǎn)矩和轉(zhuǎn)矩角振蕩劇烈，磁鏈也在波動。表明此時轉(zhuǎn)矩角已超過了最大轉(zhuǎn)矩角，導致電機運行失步。

圖11波形表明，基于轉(zhuǎn)矩角限幅SVM－DTC的PMSM系統(tǒng)，在轉(zhuǎn)矩角達到最大轉(zhuǎn)矩角之前，轉(zhuǎn)速不斷上升，轉(zhuǎn)矩角不斷增大，電流幅值維持為最大幅值;而在轉(zhuǎn)矩角接近最大轉(zhuǎn)矩角時，由于受到轉(zhuǎn)矩角限幅控制，轉(zhuǎn)矩角變化趨緩，與圖4所示的最大轉(zhuǎn)矩角的變化規(guī)律一致，最終在轉(zhuǎn)速達到給定值之后轉(zhuǎn)矩角降至零。當轉(zhuǎn)矩角隨最大轉(zhuǎn)矩角的限制逐漸減小時，電流的幅值隨之減小，與MPTV階段的運行階段特性相似。從圖中可發(fā)現(xiàn)，實際轉(zhuǎn)矩角開始減小的時刻在t=0.2 s，而此時實際轉(zhuǎn)矩角尚未達到最大轉(zhuǎn)矩角。這是因為實施限幅的對象是給定轉(zhuǎn)矩角，而非實際轉(zhuǎn)矩角，故其開始限幅的時刻主要由轉(zhuǎn)矩PI控制器的輸出決定，從而導致實際轉(zhuǎn)矩角的提早減小。同時可看出，由于是轉(zhuǎn)矩角開環(huán)控制，實際轉(zhuǎn)矩角與最大轉(zhuǎn)矩角之間存在一定差值，即實際轉(zhuǎn)矩角的軌跡不是最大轉(zhuǎn)矩角的軌跡。

由圖12可看出，基于給定轉(zhuǎn)矩改進SVM－DTC的PMSM系統(tǒng)，隨著轉(zhuǎn)速的升高，轉(zhuǎn)矩角不斷增大。同時A相電流幅值始終保持最大，表明此方法充分利用了電機極限容量。而且當轉(zhuǎn)矩角超過最大轉(zhuǎn)矩角之后，系統(tǒng)依然穩(wěn)定運行。

6 結(jié)論

1)系統(tǒng)地分析了PMSM基于MTPA、CPSR和MTPV 3種算法的特點以及轉(zhuǎn)矩角的情況，總結(jié)出DTC方式下PMSM弱磁高速運行時轉(zhuǎn)矩角超過其最大值是系統(tǒng)失穩(wěn)的關鍵。

2)提出了基于轉(zhuǎn)矩角限幅的DTC方法，可有效限制轉(zhuǎn)矩角，使得PMSM能在轉(zhuǎn)矩角限幅階段運行于類MTPV算法，獲得最大轉(zhuǎn)矩，確保PMSM高速運行時的穩(wěn)定性。

3)提出了基于轉(zhuǎn)矩給定改進計算方法的DTC策略，能有效提高系統(tǒng)的參數(shù)魯棒性，實現(xiàn)同時滿足電流和電壓限幅狀態(tài)下的高速穩(wěn)定運行，更有效地拓寬了PMSM的高速運行范圍。

4)兩種方法均可保持PMSM DTC系統(tǒng)優(yōu)異的動態(tài)性能，且計算方便。

［1］ZHONG L，RAHMAN M F，HU W Y，et al.Analysis of direct torque control in permanent magnet synchronous motor drives［J］.IEEE Transactions on Power Electronics，1997，12(3):528－536.

［2］TANG L X，ZHONG L，RAHMAN M F，et al.A novel direct torque controlled interior permanent magnet synchronous machine drive with low ripple in flux and torque and fixed switching frequency［J］.IEEE Transactions on Power Electronics，2004，19(2):346－354.

［3］孫丹，賀益康.基于恒定開關頻率空間矢量調(diào)制的永磁同步電機直接轉(zhuǎn)矩控制［J］.中國電機工程學報，2005，25(12):112－116.

SUN Dan，HE Yikang.Space vector modulated based constant switching frequency direct torque control for PMSM［J］.Proceedings of the CSEE，2005，25(12):112－116.

［4］裘君，趙光宙.永磁同步電機磁鏈自適應控制［J］.電機與控制學報，2009，13(6):798－803，810.

QIU Jun，ZHAO Guangzhou.Flux adaptive control of PMSM［J］.Electric Machines and Control，2009，13(6):798－803，810.

［5］賈洪平，孫丹，賀益康.基于滑模變結(jié)構(gòu)的永磁同步電機直接轉(zhuǎn)矩控制［J］.中國電機工程學報，2006，26(20):134－138.

JIA Hongping，SUN Dan，HE Yikang.The PMSM DTC based on variable structure sliding mode［J］.Proceedings of the CSEE，2006，26(20):134－138.

［6］萬健如，宮成，劉暐，等.基于MTPA的永磁同步電機滑模變結(jié)構(gòu)直接轉(zhuǎn)矩控制［J］.電機與控制學報，2012，16(3):30－35.

WAN Jianru，GONG Cheng，LIU Wei，et al.Sliding mode variable structure control of permanent magnet synchronous machine based on MTPA［J］.Electric Machines and Control，2012，16(3):30－35.

［7］KWANG Woon Lee，SANG Bin Lee.MTPA operation point tracking control scheme for vector controlled PMSM drives［C］//International Symposium on Power Electronics Electrical Drives Automation and Motion(SPEEDAM)，June 14－16，2010，Pisa.2010:24－28.

［8］MORIMOTO S，TAKEDA Y，HIRASA T，et al.Expansion of operating limits for permanent magnet motor by current vector control considering inverter capacity［J］.IEEE Transactions on Industry Applications，1990，26(5):866－871.

［9］RAHMAN M F，ZHONG L，KHIANG W L.A direct torque-controlled interior permanent magnet synchronous motor drive incorporating field weakening［J］.IEEE Transactions on Industry Applications，1998，34(6):1246－1253.

［10］竇汝振，溫旭輝.永磁同步電動機直接轉(zhuǎn)矩控制的弱磁運行分析［J］.中國電機工程學報，2005，25(12):117－121.

DOU Ruzhen，WEN Xuhui.Analysis of field weakening operation for the direct torque control of PMSM［J］.Proceedings of the CSEE，2005，25(12):112－116.

［11］INOUE Y，MORIMOTO S，SANADA M.A novel method of maximum-power operation for IPMSMs in DTC system［C］//13th European Conference on Power Electronics and Applications，September 8－10，2009，Barcelona.2009:1－10.

［12］INOUE Y，MORIMOTO S，SANADA M.Control method suitable for direct-torque-control-based motor drive system satisfying voltage and current limitations［J］.IEEE Transactions on Industry Applications，2012，48(3):970－976.