某型航空發動機前支承動剛度的有限元分析
丁哲民
(長沙航空職業技術學院,湖南 長沙 410124)
影響發動機振動特性的主要因素包括航空發動機靜子支承動剛度,精準的靜子系統動力特性是研究轉子系統動力特性中臨界轉速、振型、不平衡響應以及傳遞特性的前提。現有文獻表明,轉子和機匣間的動力耦合關系是用支承動剛度表征的。支承動剛度是頻率的函數,與轉子的臨界轉速密切相關,體現了在研究機匣支撐系統的頻率范圍內,位移響應和激振力的關系。所以在設計發動機時,獲得動剛度隨頻率的變化曲線是分析支承動剛度的重要條件。
目前航空發動機支承結構的剛度系數的范圍都是靠經驗給出的,數據的準確性對轉子特性計算至關重要。現階段獲得航空發動機支承結構剛度系數的主要手段分試驗和數值模擬計算兩種方法。但是通過試驗方法獲得結果受很多因素制約。(例如:試驗儀器精度差;費時費力費錢)。隨著計算力學的發展和大型分析軟件的開發,在結構動力學分析領域中,經常使用有限元進行計算,所以靜子系統的動力特性用計算的方法求出是很有必要的。
1 發動機前支撐的動力模型
使用有限元的計算方法,計算模型航空發動機前支承動剛度,建立某型航空發動機前支承結構的三維實體模型,為后續計算做準備,這些原始數據不僅直接影響到網格的劃分,而且還會影響計算結果。由于某型航空發動機前支承具有復雜的結構,建立三維實體模型要適當的簡化其中的結構。在保證充分反映力學特性和結構特性的前提下,對所關心的某型航空發動機前支承結構模型關鍵地方精細化,對不關鍵的區域,在不影響關鍵地方結構特性的情況下進行最大程度簡化。某型航空發動機前支承結構主要為壓氣機靜子,由前機匣、后機匣、進氣機匣、第二、三、四、五級整流器組成。針對前支承動剛度的計算要求,根據實際結構尺寸,利用UG三維建模軟件建立準確的實物模型。圖1是模型航空發動機前支承實體模型內部結構。圖2是某型航空發動機前支承結構三維實體模型。
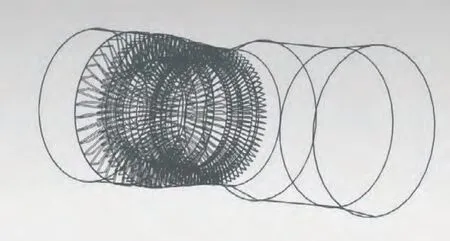
圖1 某型航空發動機前支承實體模型內部結構

圖2 某型航空發動機靜子支承結構三維實體模型
2 計算力學模型
2.1 建立有限元模型
有限元的基本思想:將表示結構的連續體離散為若干個子域,單元之間通過其邊界上的節點連接成組合體。將某型航空發動機前支承結構的三維實體UG模型導入ANSYS軟件,選擇合理的單元類型,確定合適的單元尺寸,建立某型航空發動機前支承結構的有限元模型。某型航空發動機前支承結構是由不用結構、不用形狀、不同厚度的壓氣機機匣、靜子葉片等部件構成,結構非常復雜。通過認知分析,選擇子域類型為SOLID95。SOLID95是3維8節點實體子域,子域定義20個節點,具有應力剛度、蠕變、大變形、大應變和蠕變能力。它可以保證不規則的形狀的精確度損失較小,具有協調的位移性質函數,對模型的曲線邊界的擬合能力強。通過多次試驗和分析,將用有限元的方法劃分模型航空發動機前支承結構,其網格單元尺寸設置為22mm左右,在保證計算精度的同時,確保了有限元計算規模不會太大。考慮到模型結構較為復雜,采用自動網格劃分,合理設置劃分精度,控制網格大小疏密,有效的確保了最終的有限元模型的合理性。共劃分得到913888個子域,325542個節點。圖3是模型航空發動機前支承結構有限元模型。

圖3 某型航空發動機前支承結構有限元模型
2.2 有限元分析理論
有限元法的分析過程是先分后合。即先進行單元分析,在建立了單元剛度方程以后,再進行整體分析,把這些方程集成起來,形成求解區域的剛度方程,稱為有限元位移法基本方程。
采用虛位移原理建立的整體剛度方程就是整體結構上所有節點載荷所做的虛功等于所有單元的虛應變能之和,即
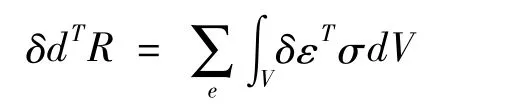
式中 δd= [δd1δd2… δdN]T為整體節點位移虛位移向量。將虛應變與節點位移之間的關系代入,可得
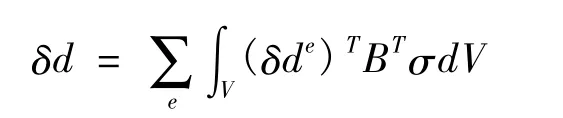
將單元節點位移向量de轉化為整體節點位移向量d,即引入變換矩陣Ae,有
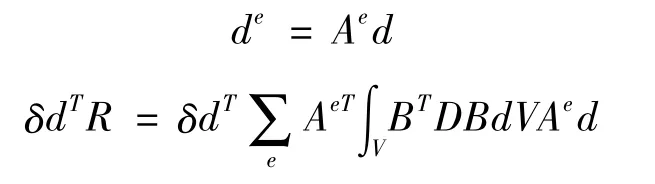
考慮到虛位移的任意性,等式兩邊與δd相乘的矩陣應該相等,得到整體平衡方程
Kd=R
3 有限元計算
3.1 有限元計算物理模型
按照某型航空發動機在機體上的實際安裝情況確定計算模型的邊界條件,對所建立的某型航空發動機前支承結構有限元模型進行模態分析。某型航空發動機通過主安裝節和輔助安裝節固定在飛機上,主安裝節三個支承位于靠近發動機重心的第六級壓氣機機匣上。燃燒室外套的后安裝邊上方兩側是輔助安裝節。對安裝節加以約束。圖4是模型航空發動機前支承結構有限元模型。在給出的邊界條件下,對該模型進行模態計算,計算頻率范圍為0—2000Hz。由計算得到前八階模態圖。圖5為某型航空發動機前支承結構前八階模態頻率。

圖4 某型航空發動機前支承結構有限元模型約束圖
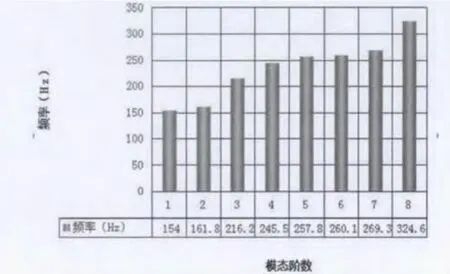
圖5 某型航空發動機前支承結構前八階模態頻率
3.2 有限元計算結果
因為結構本身參數決定動剛度的理論值,作用力的大小對動剛度的理論值沒有影響。對壓氣機靜子機匣前支承施加水平方向、垂直方向的激振力,分析機匣前支承垂直方向、水平方向的諧響應。所以,在研究模型航空發動機靜子支承系統前支承結構諧響應時,在某型航空發動機靜子支承系統前支承處加1000N的簡諧激振力,求解在每一個自由度上的諧位移。計算頻率范圍為0~300Hz。為確保計算結果的準確性和可比性,分別在靜子支承系統前支承處選取4個不同節點,分別對其進行諧響應分析,將計算前支承的4個節點沿水平方向和沿垂直方向的頻率響應曲線分別繪在一幅圖上,如圖6和圖7所示。
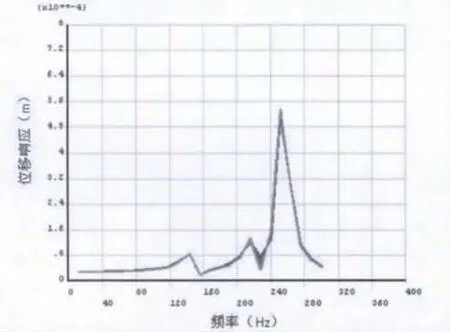
圖6 某型航空發動機前支承沿水平方向頻率響應曲線
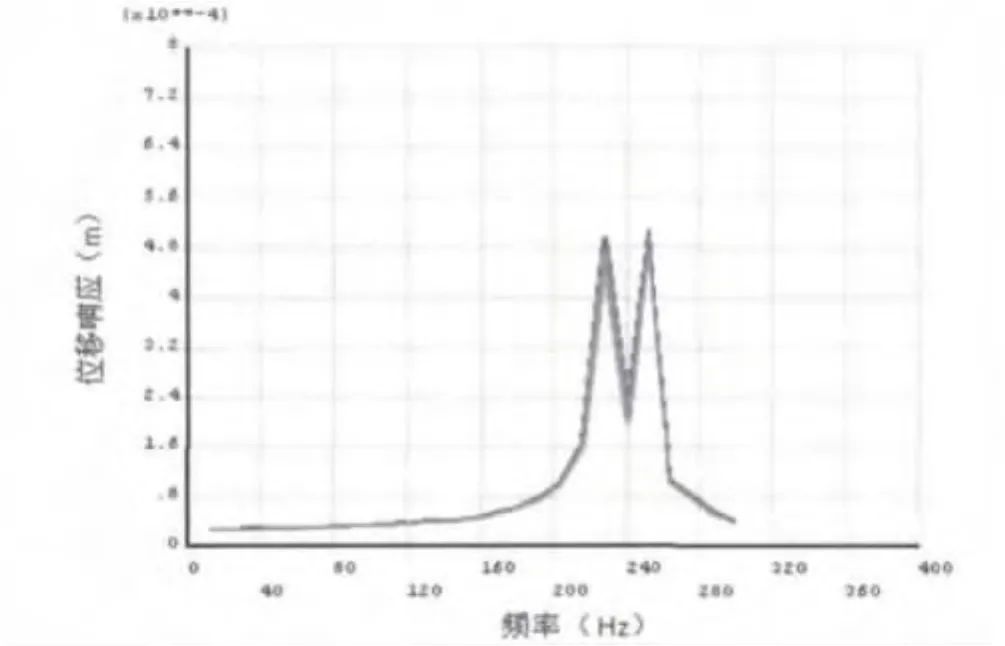
圖7 某型航空發動機前支承沿垂直方向頻率響應曲線
由圖6前支承沿水平向頻率響應曲線和圖7前支承沿垂直向頻率響應可以看出:
(1)所計算發動機靜子支承系統前支承4個節點沿水平方向動剛度隨頻率變化曲線基本上重合,計算前支承4個節點沿垂直方向剛度隨頻率變化應曲線也基本重合。
(2)激振頻率在0-300Hz時,在水平方向隨著頻率變化,靜子支承系統前支承的動剛度值有三處突降,這三處分別是 144Hz、216Hz、252Hz處,這幾個頻率正是頻率響應曲線在水平方向上出現共振峰的位置,上面頻率所對應的剛度極小值分別為1.2109× N/m、0.7889 ×N/m、0.1912 ×N/m;而在垂直方向隨著頻率變化,靜子支承系統前支承的動剛度值在228Hz和252Hz兩處出現剛度突降,這兩個頻率是頻率響應曲線在垂直方向上出現共振峰的位置,對應的剛度極小值為0.2193×N/m、0.2082×N/m。
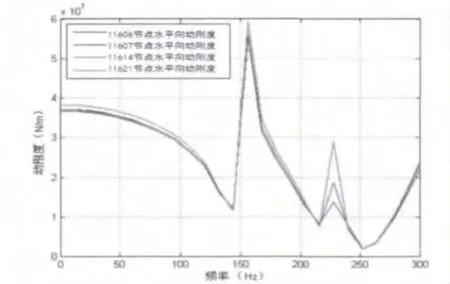
圖8 前支承沿水平方向剛度隨頻率變化對比圖
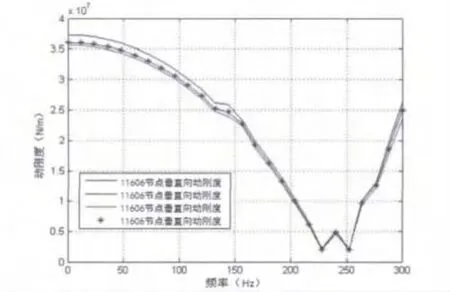
圖9 前支承沿垂直方向剛度隨頻率變化對比圖
對某型航空發動機前支承動剛度計算結果進行了簡單驗證,通過對有理論解的簡單梁進行建模、模態分析、諧響應分析、動剛度計算,驗證計算方法及參數設置的的正確性。并且將所得到的某型航空發動機前支承的諧響應分析結果與模態分析結果進行對比。前支承沿水平方向、垂直方向剛度隨頻率變化對比圖分別如圖8、圖9所示。通過對比發現二者吻合良好。在一定程度上驗證了計算結果的合理性。
4 結論
(1)對于航空發動機靜子系統這樣復雜的結構進行有限元分析,需要對結構進行簡化。本文采用的對壓氣機葉片、前機匣、壓氣機后機匣等部件分別進行簡化,然后整體建立有限元模型的簡化方法是可行的。
(2)與8節點的實體單元相比,在計算靜子系統動力特性時20節點實體單元建模具有更高的精度。基于20節點的實體單元可以更好的適應不規則的形狀,同時又不會損失太多的精確度,應用其進行靜子系統動力特性計算時,得到的結果更為精確。
(3)某型航空發動機前支承沿水平方向的動剛度曲線在0Hz處為3.662×107N/m,隨著頻率的增大而減小,在144Hz處為1.267×107N/m,在156Hz處增大到5.867×107N/m,之后又隨頻率的增大而下減小,在216Hz處為0.817×107N/m;沿垂直方向的動剛度曲線在 0Hz處為 3.626×107N/m,隨著頻率的增大而減小,在216Hz處為0.286 ×107N/m。
[1]張大義,母國新,洪杰.航空發動機轉子支承系統剛度計算中的幾個問題[J].戰術導彈技術,2005,(2).
[2]周明,倪緯斗,于文虎,等.某單軸式燃氣輪機支承剛度計算分析[J].山東電力技術,1998,(2).
[3]饒壽期.有限元法和邊界元法基礎[M].北京:北京航空航天大學出版社,1990.
[4]劉長福,鄧明.航空發動機結構分析[M].西安:西北工業大學出版社,2006.
[5]杜平安,甘娥忠,于亞婷.有限元法——原理、建模及應用[M].北京:國防工業出版社,2006.

