基于新閾值函數的小波閾值降噪方法

宋倩倩，雙 凱

（中國石油大學（北京），北京，102249）

在信號的降噪問題中，小波降噪得到廣泛應用，其中的模極大值和閾值降噪是最常用的兩種方法。由于小波閾值降噪方法其實現簡單、計算量小，從而在實際中得到廣泛研究。小波閾值降噪算法中，小波最優分解層數的確定，以及小波閾值函數的選擇，成為小波閾值降噪方法的關鍵[1-3]。

在小波閾值降噪中，文獻[4]提出的傳統硬閾值法可以很好地保留信號邊緣等局部特征，然而在一些不連續點處有時會存在偽吉布斯現象。文獻[5]提出的軟閾值法克服了硬閾值存在的連續性差的問題，然而存在過于光滑而失去信號真實性的缺點。文獻[6]提出的半軟閾值法降噪效果雖略優于硬閾值和軟閾值，但半軟閾值函數形式與硬閾值、軟閾值相同，信噪比改變不大。文獻[7]提出的新閾值函數調節因子過多，而且沒有給出如何針對不同的信號和噪聲選取最合適的值。

本文針對小波閾值算法提出了一種新的閾值函數，在最優分解層數確定的基礎上，采用傳統閾值函數、改進閾值函數進行小波閾值降噪，通過matlab進行仿真，以信噪比SNR為性能指標，發現改進閾值函數優于傳統閾值函數。同時發現，改進閾值函數選用閾值選取規則保守的minimaxi閾值，降噪效果優于其他閾值選取規則。

1 小波分析理論

根據小波Ψ(x)和尺度函數φ(x)為函數f(x)∈L2(R)定義小波序列展開[8]，可知

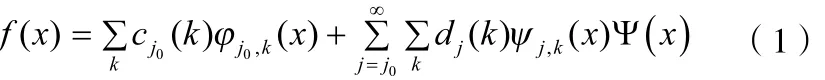
其中，j0是任意開始尺度，Cj0(k)是近似值或尺度系數，dj(k)是細節或者小波系數。

小波分析，將信號分解到不同的分辨率上，像放大鏡一樣對信號在不同頻帶上進行分析。小波分析，解決了傅里葉分析不能解決的許多難題，使得信號可以同時具有時間域和頻率域的信息。在低尺度上，具有較高的頻率分辨率和較低的時間分辨率，在高尺度上具有較高的時間分辨率和較低的頻率分辨率。

2 小波閾值降噪

小波變換具有一種“集中”的能力。經過小波變換后，有用信號對應的小波系數有很好的能量集中性，其幅值偏大，并且數量較少；而噪聲信號對應的小波系數，能量比較平均，個數較多，但幅值偏小。利用含噪信號的這個特點，就可以通過合適的閾值函數將噪聲對應的小波系數置零，從而實現有用信號的提取[9]。

一維含噪信號的小波閾值降噪處理過程步驟如下：

1）小波分解。選擇一個合適的小波基，并通過白噪聲檢驗來確定分解層數N，然后對信號進行N層小波分解。

2）小波系數的閾值處理。對第一層到第N層的高頻系數，選取合適的閾值，根據相應的閾值函數進行閾值量化處理。

3）小波重構。對閾值處理過的小波系數，進行一維信號的小波重構。

2.1 閾值的選取

閾值的選取有4種原則：Stein風險閾值（rigrsure準則）、通用閾值（sqtwolog準則）、極大極小閾值法（minimaxi準則）、啟發式閾值法（heursure準則）[10]。

4種閾值方法中，rigrsure準則和minimaxi準則的閾值選取較為保守，sqtwolog和heursure準則的閾值選取則較為過度，有可能將有用信號的高頻部分當做噪聲信號去除掉。本文選取保守的minimaxi閾值。

2.2 小波閾值函數

2.2.1 傳統硬閾值和軟閾值方法

硬閾值方法，是把絕對值小于閾值t的小波系數直接置零，其余的小波系數全部保留，實現信號的重構。硬閾值法的圖像如圖1（a）所示，公式為：

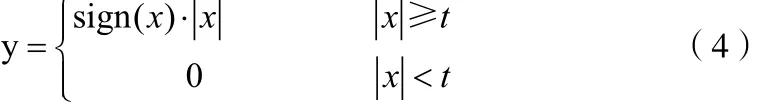
軟閾值方法，是一種基于硬閾值法的改進，將硬閾值中保留的系數，絕對值減少t，再實現信號的重構。軟閾值法的圖像如圖1（b）所示，公式為：

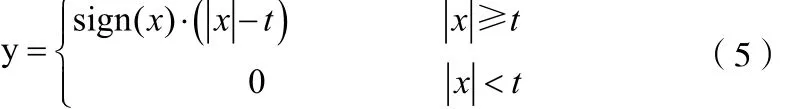
半軟閾值方法，是對軟、硬閾值法的一種折中方法，其函數值介于軟閾值和硬閾值之間，在降噪中起到了很好的效果[11]。半軟閾值的圖像如圖1（c）所示，公式為：

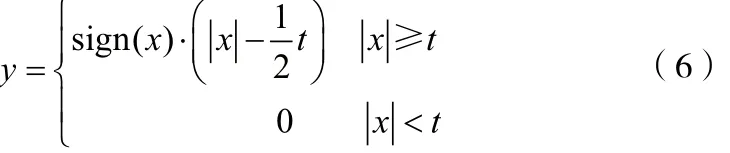
硬閾值函數在閾值處x=t是不連續不可導的，從而影響了信號重構的效果，帶來了一些附加振蕩，使信號光滑性很差。軟閾值光滑性好，克服了硬閾值不夠平滑的特點，但同時也由于過于平滑而損失了一些有用的高頻信息，影響了重構的真實。半軟閾值考慮到軟硬閾值的缺點，是一種折中方法，取得了一定的降噪效果。本文針對傳統閾值函數的缺點，提出兩種改進閾值函數。

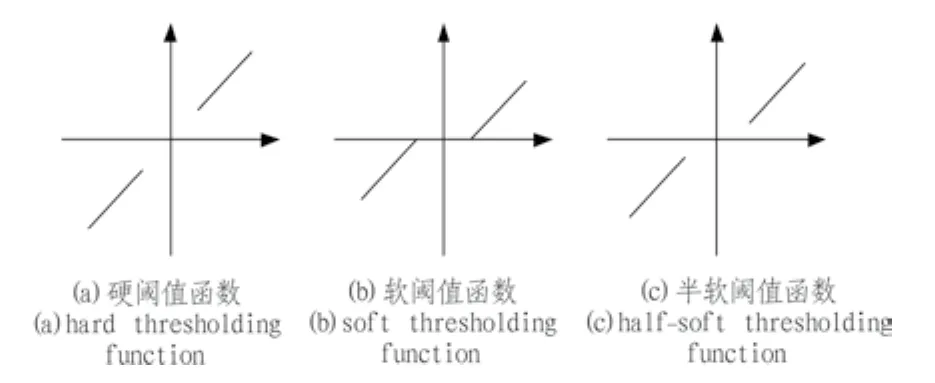
圖1 傳統閾值函數Fig.1 Traditional threshold function

2.2.2 改進閾值函數1

在硬閾值基礎上進行改進，使其在保留了硬閾值函數優點的同時，又增加了連續性，以及光滑性。在閾值附近的區間(-(2-α)t, -t)∪(t, (2-α)t)上滿足二次拋物線函數x= (1/m)y2+t，在剩余區間(-∞, -(2-α)t)∪((2-α)t, +∞)內滿足硬閾值函數，在連接點x= (2-α)t處連續且可導。函數圖像如圖2所示，公式如下：

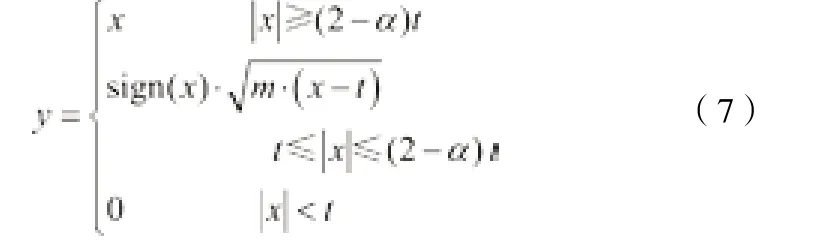
其中，m= 4(1-α)t,α∈ (0, 1)。

當α= 0時，接近于硬閾值，在區間(-2t, -t)∪(t, 2t)上滿足拋物線函數，在(-∞, -2t)∪(2t, +∞)上滿足硬閾值函數；當α= 1時，為軟閾值函數；當α= 1/2時，接近于半軟閾值，在區間(-3t/2, -t)∪(t, 3t/2)上滿足拋物線函數，在(-∞,-3t/2)∪(3t/2, +∞)上滿足硬閾值函數。α越接近于1，滿足拋物線函數的區間越大，α越接近于0，滿足拋物線函數的區間越小。

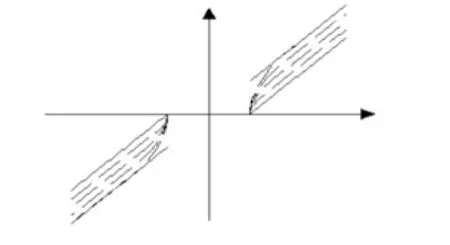
圖2 改進閾值函數1Fig.2 Improved threshold function 1

2.2.3 改進閾值函數2

考慮到改進函數1到達硬閾值函數的區間太長，提出一個更快接近于硬閾值函數的函數。改進閾值函數1在區間(-(4-α)t/3, -t)∪(t, (4-α)t/3)上滿足一個四次函數x= (1/m)y4+t，改進閾值函數1在區間(-∞, -(4-α)t/3)∪((4-α)t/3,+∞)上滿足硬閾值函數，該函數在x= (4-α)t/3處連續且可導。此函數比改進硬閾值函數1能夠以更快的速率連接到硬閾值函數。函數圖像如圖3所示，公式如下：

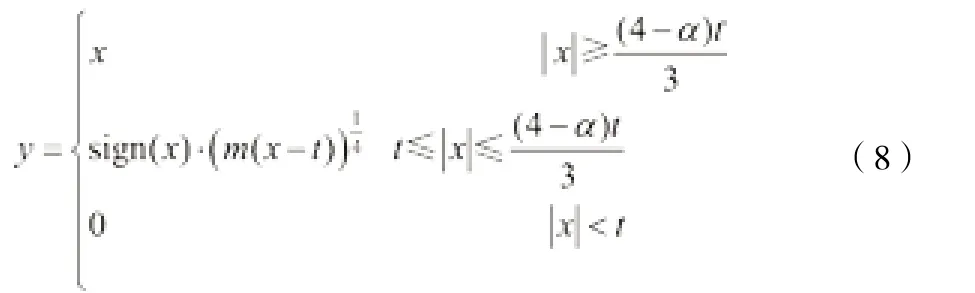
其中，m= 256[(1-α)t]3/27,α∈ (0, 1)。

當α= 0時，接近于硬閾值，在區間(-4t/3, -t)∪(t, 4t/3)上滿足拋物線函數，在(-∞, -4t/3)∪(4t/3, +∞)上滿足硬閾值函數；當α= 1時，為軟閾值函數；當α= 1/2時，接近于半軟閾值，在區間(-7t/6, -t)∪(t, 7t/6)上滿足拋物線函數，在(-∞, -7t/6)∪(7t/6, +∞)上滿足硬閾值函數。α越接近于1，滿足拋物線函數的區間越大，α越接近于0，滿足拋物線函數的區間越小。

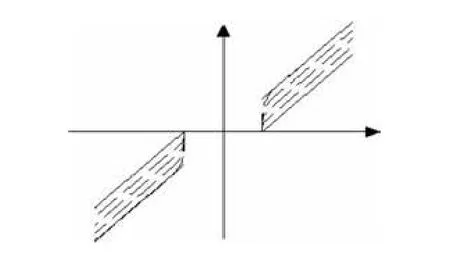
圖3 改進閾值函數2Fig.3 Improved threshold function 2

閾值附近的系數混雜了干凈信號的小波系數和噪聲的小波系數，單純閾值的選取無法改變這一問題。新改進的新閾值函數，將閾值 附近的系數做一定的能量壓縮，從而在一定程度上壓縮了噪聲對干凈信號的影響，同時又保留了部分干凈信號的信息。兩種改進的新閾值函數對閾值附近的系數做了不同程度能量的壓縮，改進閾值函數1對小波系數的壓縮區間長，而改進閾值函數2對小波系數的壓縮區間短，要根據具體情況來選擇這兩種函數，以及合適的α值。

3 仿真驗證

為了比較上述改進閾值降噪方法的降噪效果，引入如下信噪比定義：

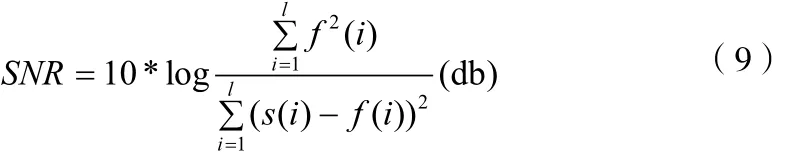
其中：f(i)為真實信號，s(i)為含噪聲信號，L為信號長度[12]。

采用db6小波函數，在疊加白噪聲信噪比為3的情況下，對blocks信號，首先得出其最優分解層數為6層，然后采用改進閾值函數1和2進行降噪，并與傳統硬閾值、軟閾值、半軟閾值進行比較，降噪后的信噪比如圖4所示。

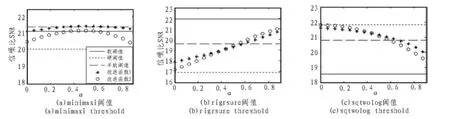
圖4 blocks信號仿真Fig.4 Blocks signal de-noising of improved threshold function

圖4可以看出，minimaxi閾值用在改進閾值函數中降噪效果最優，改進閾值函數總體降噪效果優于傳統閾值函數。同時對于不同的α，降噪效果不同。在傳統3種方法中，當硬閾值較優時，α貼近于1時效果更好；當軟閾值較優時，α貼近于0效果更好。改進函數1和改進函數2總體走勢相同，但不同的信號，不同的α值，去噪效果不同。

4 結 論

文中提出了一種壓縮能量閾值函數，仿真發現，該函數采用minimaxi閾值可使改進閾值函數信噪比達到最優，兩種改進閾值函數與傳統閾值法相比，有著明顯的降噪效果。在實際應用中，應該根據具體的信號具體的噪聲采用不用的降噪策略，使得降噪效果達到最優。

[1]文莉,劉正士,葛云建.小波去噪的幾種方法[J].合肥工業大學學報:自然科學版,2002,25(2):167-172.

WEN Li, LIU Zheng-shi, GE Yun-jian. Several methods of wavelet de-noising[J].Journal of He fei University of Technology:Natural Science,2002,25(2):167-172.

[2]喬強,周激流,何坤等,基于小波變換的非平穩信號去噪[J].

計算機應用研究, 2005 (8):161-166.

QIAO Qiang, ZHOU Ji-liu, HE Kun, et al. Noise reduction of non-stationary signal based on wavelet transform[J].Application Research of Computers, 2005(8):161-166.

[3]張翠芳.小波閾值降噪效果影響因素的研究[J].西安郵電學院學報,2008,13(5):13-15.

ZHANG Cui-fang. Research on the influence factors of wavelet threshold de-noising[J]. Journal of Xi'An University of Post and Telecommunications, 2008,13(5):13-15.

[4]Dohono D L, Johnstone I. Ideal spatial adaptation by wavelet shrinkage[J].biometrika, 1994,81(3):425-455.

[5]Dohono D L.Denoising by soft—thresholding[J].IEEE Transaction on Information,1995,41(3):613-627.

[6]栗鳴，郭東敏，權建峰,等.基于提升小波的改進半軟閾值降噪方法[J],探測與控制學報,2009,31(4):54-57.

LI Ming, GUO Dong-min, QUAN Jian-feng,et al. Improved halfsoft threshold de-noising based on liftingwavelet[J]. Journal of Detection & Control, 2009,31(4):54-57.

[7]趙天嬌,何選森,陳利.基于新閾值函數小波變化的噪聲盲分離算法[J].計算機應用研究,2010,27(8): 2886-2888.

ZHAO Tian-qiao, HE Xuan-sen, CHEN Li. Noisy blind source separation algorithm based on new threshold function of wavelet transform[J]. Application Research of Computers. 2010,27(8):2886-2888.

[8]Rafael C. Gonzalez, Richard E. Woods. 數字圖像處理[M].2版.阮秋琦,阮宇智,譯.北京:電子工業出版社,2003.

[9]潘泉，張磊，孟晉麗等.小波濾波方法及應用[M].北京:清華大學出版社, 2005:58.

[10]胡澤,林麗君,何明格,等.基于小波變換的隨鉆測試數據降 噪方法研究[J].西南石油大學學報:自然科學版,2011, 33(1):165-169.

HU Ze, LIN Li-jun, He Ming-ge, et al. Research of de-noising oil-drilling testing data based on wavelet[J]. Journal of Southwest Petroleum University: Science & Technology Edition, 2011,33(1):165-169.

[11]劉俊星，章新華，周波等.新閾值及閾值函數的小波去噪研究,聲學技術[M].上海:聲學技術出版社, 2011.

[12]錢穎雪，左洪福，李耀華.小波與傅里葉變換耦合的靜電監測信號去噪法[J].計算機技術與發展,2009,19(7):1-3.

QIAN Ying-xue, ZUO Hong-fu, LI Yao-hua. Static monitoring signal de-noising by wavelet and FFT[J]. Computer Technology and Development, 2009,19(7):1-3.