基于蒙特卡羅仿真與逆向FTF的復雜系統可靠性分析
魯 靖,卞樹檀,周 帥
(第二炮兵工程大學,西安710025)
基于蒙特卡羅仿真與逆向FTF的復雜系統可靠性分析
魯 靖*,卞樹檀,周 帥
(第二炮兵工程大學,西安710025)
失效模式影響及危害性分析(FMECA)和故障樹分析(FTA)是復雜系統可靠性分析的常用方法,兩者各有優缺點。FMECA是一種歸納性分析方法,它對系統、部件的各種故障原因及模式等進行詳盡分析,進而提出改進補償措施,該方法運算簡單,但存在對大型、復雜系統的分析工作量大、周期長,分析結果的表達直觀性、邏輯性較差等不足。故障樹分析法(FTA)是一種演繹性分析方法,它首先選擇“不希望事件”為頂事件,自上而下對故障因素追根究底。該方法表達直觀明了,常用于多重故障引起的故障的分析,但故障樹的建造及計算過程較復雜,限制了底事件的數量,因此復雜系統的FTA難以做到對事件進行詳盡、細致的研究[1-4]。
通過上述分析,本文提出了一種基于FTA仿真與FMECA相結合的逆向FTF綜合分析方法,該方法充分汲取了FTA與FMECA各自的優點,彌補了常規FTF分析存在的不足[8-9],具有較高的精度和實用價值。
1 故障樹仿真運行
1.1 故障樹仿真模型
設系統由n個基本單元組成,則系統F可表示為:F={Z1,Z2,…,Zi,…,Zn},式中,Zi(i=0,1,…,n)表示系統的n個基本單元,且已知每個基本單元失效分布函數為Fi(t)(t=1,2,…,n)。
故障樹就是系統中各基本單元間的邏輯關系圖,因此,可以用系統故障樹來表示仿真時的邏輯關系:xi是表示基本單元Zi的狀態變量,為故障樹的底事件,Y為系統F的頂事件,則頂事件Y的狀態φ完全由底事件xi所決定,通過故障樹的各種邏輯門運算,可得到系統的結構函數φ(x),即:
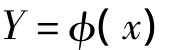
結構函數φ(x)是表示系統狀態的一種布爾函數,變量x則是各組成單元狀態的集合,它們的狀態有1 (正常)、0(故障)兩種,引入時間參量的情況下,單元狀態向量Xi(t)表示第i個底事件的狀態變量,結構函數Φ(t)表示頂事件在時間t時刻的狀態變量:

定義:故障樹的最小割集就是引起頂事件發生所必須的最低限度的基本事件集合。
故障樹建立后,寫出故障樹的結構函數,求出系統的故障的最小割集M(x),設系統的故障樹含有k個最小割集,用Mi(x)(1,2,…,k)表示第i個最小割集的狀態。由最小割集定義可知,只要有一個最小割集發生,則頂事件必然發生。顯然,系統結構函數又可以表示為:
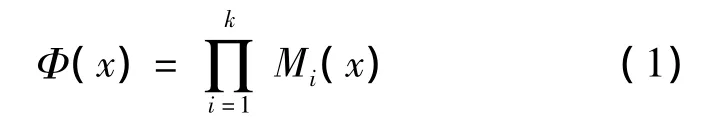
1.2 仿真運行
系統故障樹仿真的基本思路[6]:根據最小割集定義及式(1)可知,當對系統進行蒙特卡羅仿真時,系統的失效時間與最早失效的故障樹最小割集的時間相等,因此,可以直接對故障樹每個最小割集的失效時間進行抽樣,把這些最小割集失效時間的最小值作為系統失效的時間的一個抽樣值,記錄此故障時間。重復此過程,最后通過對記錄樣本進行數據統計分析,得到各種可靠性結果。仿真的基本過程如下:
(1)基本事件失效時間的抽樣:用蒙特卡羅方法對每個底事件進行抽樣,取得每一個底事件失效的時間樣本。已知第i個基本部件的失效分布函數Fi(t)(t=1,2,…,n),對其進行失效時間抽樣值為:

(2)最小割集失效時間的確定:設系統故障樹中含有k個最小割集,且每個最小割集中有nk個基本事件,可得到nk個基本事件失效時間樣本ti(i= 1,2,…,nk),并記失效時間最大者為tmax,由式(1)可知,只有當最小割集中的nk個基本部件全部失效,系統才會失效,因此,最小割集k的失效時間就等于其最晚失效基本部件的失效時間,記第k個最小割集的失效時間為:

(3)系統失效時間的確定:根據最小割集的定義可知,只要有一個最小割集發生,頂事件就發生,設系統故障樹頂事件發生的時間為T,求出k個最小割集的最小發生時間后,系統失效時間記為:

(4)仿真數據的獲取:重復步驟(1)、(2)、(3)N次,可以得到N個系統失效仿真結果,依次記為: Ti(i=1,2,…,N),將Ti依次與事先設定系統規定工作時間Tn(n=1,2,…,N)進行比較,如Ti<Tn,則說明系統失效,最終可得累積失效次數MN。
1.3 重要度計算
①基本部件Zi重要度:

從上式可知,W(Zi)表示基本部件的重要程度,若W(Zi)=1,則說明基本部件Zi失效必然導致整個系統失效,因此系統的可靠性就必須關注那些重要度較高的基本部件。
②基本部件模式重要度:

有定義可見,WN(Zi)表示部件失效而引起系統失效次數在系統總失效中的百分比,模式重要度的計算可用來判斷系統可靠性設計中的薄弱環節,WN(Zi)值越大,說明該部件越是系統可靠性薄弱環節。
2 基于FTF復雜系統仿真分析全過程
故障樹仿真完成后,需要對仿真數據進行統計,計算得到基本部件Zi重要度W(Zi)和模式重要度WN(Zi),然后運用FMECA分析法對系統重要部件和薄弱環節進行FMECA綜合分析,系統可靠性分析流程如圖1所示。

圖1 FTF分析法流程圖
3 應用實例
小型多旋翼飛行器是近年來航空航天領域研究的熱點之一,由于它靈巧、機動,可用于偵查、目標指示、地質勘查、通信中繼等多種特殊任務,本文以自制四旋翼飛行器為例,以飛行器任務失敗為頂事件建立簡易故障樹如圖2,各底事件及其失效分布類型參數如表1所示。

圖2 飛行器簡易故障樹
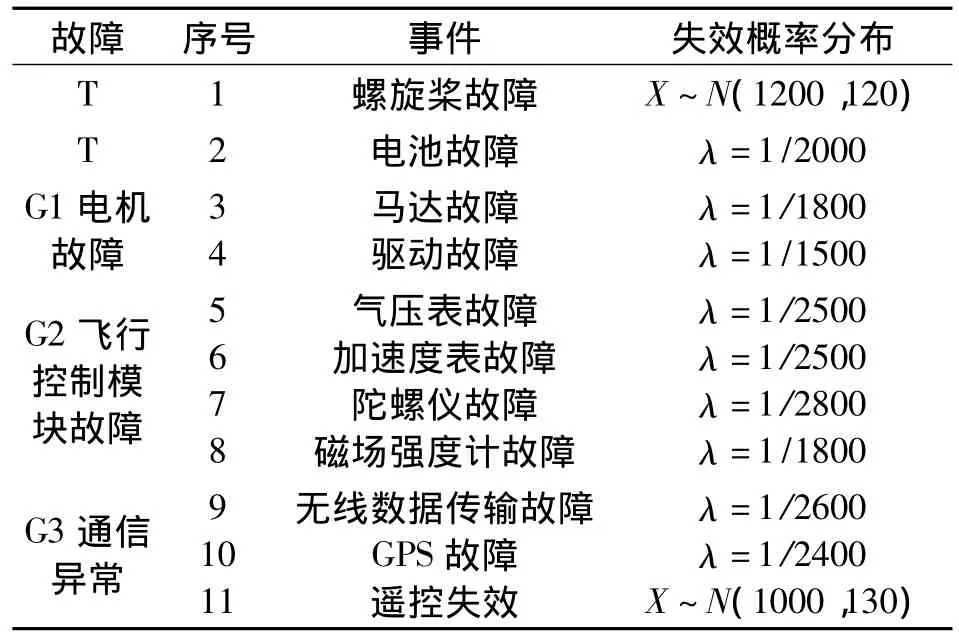
表1 自制四旋翼飛行器故障樹事件描述
蒙特卡羅方法[5]要求仿真次數足夠多,以滿足一定的仿真精度,經多次仿真可知:隨著仿真次數從1 000次增加至10 000次,仿真運行結果也逐漸趨于真值,且仿真曲線趨于光滑,波動較小,說明可靠度變化趨于穩定。
由于MATLAB軟件可以方便的產生(0,1)間的隨機數,因此,本文采用MATLAB進行仿真,仿真流程如圖3所示,現結合本例,取仿真次數N0=15 000進行仿真,計算重要度如表2。

表2 部件重要度與模式重要度仿真結果
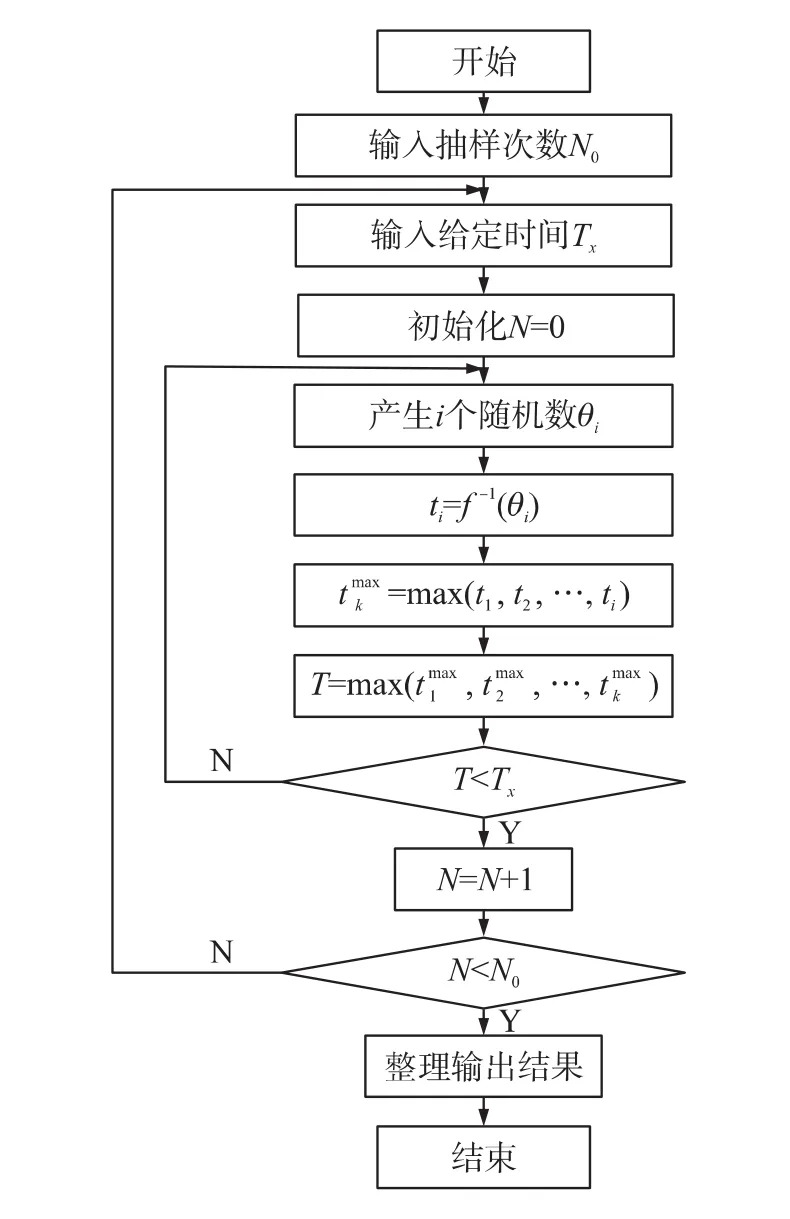
圖3 飛行器簡易故障樹
由仿真結果可知:數值的大小代表著部件在系統中的重要程度和它是否為薄弱環節。其中,代碼為7、9的基本部件重要度為零,這并不代表該部件對系統沒有任何作用,而是該部件在仿真時本身沒有出現失效,可認為部件7、部件9的可靠性較高。
針對上述仿真結果,基本事件重要度排列順序為:

對重要度較大的部件 Z4、Z1、Z3、Z2、Z11進行FMECA分析[7],如表3和表4所示。
根據表3和表4中的每一故障模式發生的概率等級和嚴重性等級繪制出各部件的危害性矩陣圖,如圖3所示,由于部件較多,為了直觀的分析危害等級,將矩陣圖轉化為危害等級直方圖,如圖4所示。
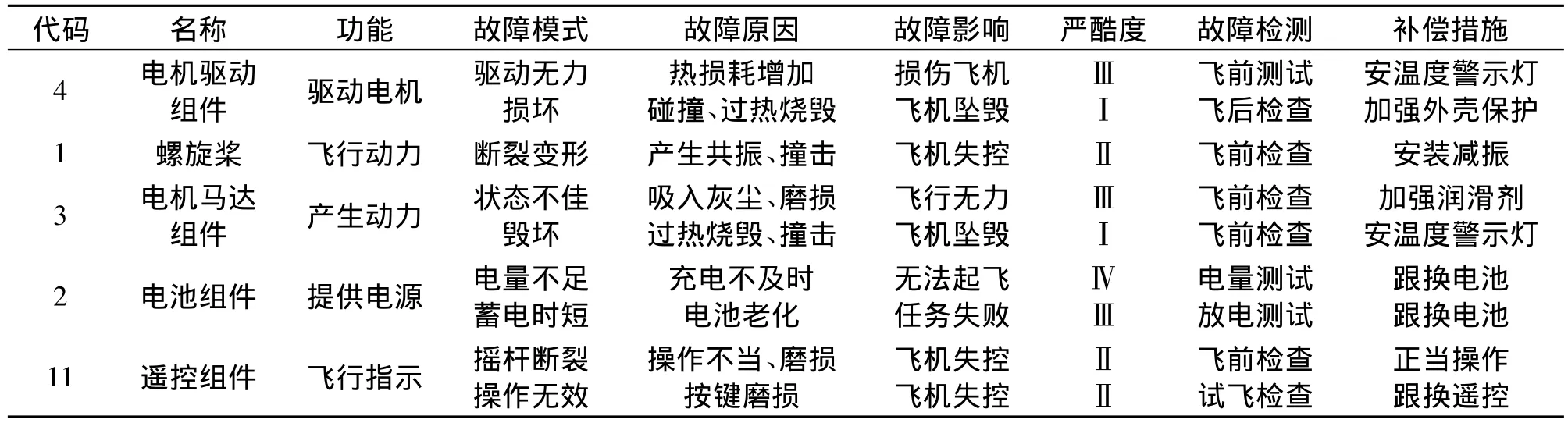
表3 自制無人機重要部件故障模式及影響分析表(FMEA)

表4 故障模式影響和致命度分析表(FMECA)(各部件的故障概率根據實際情況選取)

圖4 危害性矩陣圖
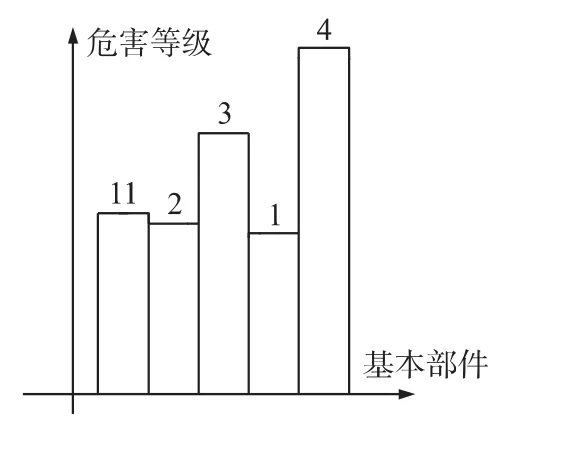
圖5 危害等級直方圖
通過上述分析,可以直觀的看到基本部件的危害等級排序:Z4>Z3>Z11>Z2>Z1,電機驅動、遙控組件及電機是小型四旋翼飛行器的可靠性的關鍵所在,其次,螺旋槳和電池也是薄弱環節,與實際試驗情況相符,在設計和使用時都需要引起高度重視。
4 結論
在工程實踐中,我們所面臨的系統往往十分龐大,詳盡的FMECA分析不僅耗時費力,還有可能遺漏系統的薄弱環節。運用蒙特卡羅方法進行仿真求取重要度可以大大降低主觀判斷的影響,很好的實現對系統進行可靠性評估,因此,在對復雜系統進行FMECA分析時,應該抓住重點和薄弱環節進行詳盡分析,為可靠性設計提供有力的參考,同時也是進行可靠性分析行之有效的方法。
[1] 曾聲奎.可靠性設計與分析[M].北京:國防工業出版社,2011.
[2] 劉永葆,韓鳳科.王開奇.逆向FTF方法在船用燃氣輪機故障分析中的應用[J].熱能動力工程,2001,16(94):450-452.
[3] 楊田,周密.謝俊.正向FTF方法在核級先導式安全閥故障分析中的應用[J].核動力工程,2010,30(1):65-69.
[4] 高峻峣,龔建偉.基于逆向FTF的履帶式移動機器人安全性分析[J].測控技術,2003,22(6):49-51.
[5] 文建國,孫作佩,陳爭新.基于故障樹的蒙特卡羅仿真在可靠性評估中的應用[J].海軍航空工程學院學報.2010,25(1):88-92.
[6] 王潔,尹海麗.蒙特卡羅方法的應用研究[J].青島理工大學學報,2006,27(2):111-113.
[7] 王彩霞.高速動車組主要零部件損傷規律及維修周期的研究[D].北京交通大學,2012:7-15.
[8] 楊繼春,范銳軍.利用FTF方法,提高測控軟件可靠性[J].測控技術,2003,22(9):46-47.
[9] 鄧曼.FTA和FMECA綜合法對常壓爐的風險分析[J].工業安全與環保,2006,32(12):51-53.
魯 靖(1988- ),男,漢族,云南曲靖人,碩士研究生,主要從事復雜大型系統可靠性評估研究,ynqjlj@163.com。
Reliability Analysis of Complex System Based on Inverse FTF Simulation
LU Jing*,BIAN Shutan,ZHOU Shuai
(The Second Artillery Engineering University,Xi’an 710025,China)
According to reliability assessment of complex system,an inverse FTF comprehensive analysis method based on integrate FTA simulation and FMECA is introduced.In the system,the important components and weaknesses point were calculated by fault tree monte carlo method.Then,the critical components were analyzed detailed by FMECA,improving the efficiency of reliability analysis and enhancing the objectivity of the reliability evaluation. And an example of a UAV was calculated and analyzed.The experimental results show that this method has guiding role and pratical value for Complex System.
reliability;complex system;Monte Carlo simulaion;inverse FTF;important calculation
針對復雜系統可靠性評估問題,提出了一種基于FTA(故障樹)仿真與FMECA(故障模式影響及危害性分析)相結合的逆向FTF綜合分析方法,該方法通過故障樹的蒙特卡羅仿真計算系統中的重要部件和系統薄弱環節,再利用FMECA有針對性的對重要部件進行詳盡分析,提高了可靠性分析的效率,增強了評估的客觀性。并以某無人機為例進行了計算和分析,結果表明:該方法對復雜系統可靠性設計具有一定的指導作用和實用價值。
可靠性;復雜系統;蒙特卡羅仿真;逆向FTF;重要度計算
TB114.3
A
1005-9490(2014)02-0341-04
2013-05-21修改日期:2013-06-13
EEACC:0240G
10.3969/j.issn.1005-9490.2014.02.037

