一類奇異三階兩點邊值問題正解的存在性

劉瑞寬

（西北師范大學數學與統計學院,甘肅 蘭州730070）

1 預備知識

三階微分方程在應用數學和物理等很多學科中有重要的應用,可以描述撓度彎曲的梁,有固定或改變交叉的部分,電磁波的傳播和重力驅動等,見文獻［1］.近年來,三階邊值問題已受到廣泛關注［2-8］.其中,文獻［2-3］中運用上下解方法研究了三階邊值問題正解的存在性,文獻［5-9］通過降階法和比較原理研究了三階兩點和多點邊值問題正解的存在性.特別地,文獻［10］運用Krasnoselskii's不動點定理研究了三階奇異邊值問題

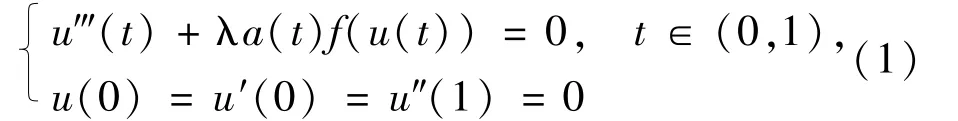
正解的存在性與多解性.文獻［11-12］通過討論相應線性算子第一特征值,給出了三階兩點邊值問題的正解存在性結果.受以上文獻的啟發,本文考慮三階兩點邊值問題（1）正解的存在性,其中允許a（t）在t＝0或t＝1處有奇性.通過對相應線性算子第一特征值的討論,運用不動點指數理論獲得當f0、f0、f∞、f∞∈（0,+∞）時正解的存在性結果,對文獻［9］結果進行了補充,并且本文得到的結果是最優的.

為了方便,記

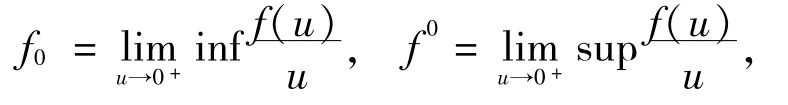
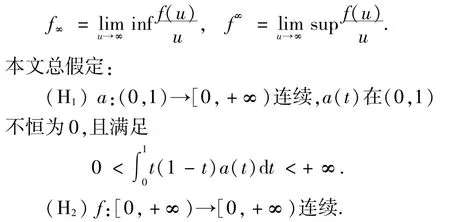
本文主要結果的證明基于下面的不動點指數理論.

定理1.1［13］設E是Banach空間,K?E為E中的一個錐.假設Ω為E中的有界開集,且T:K∩→K緊,則以下結論成立:

（i） 若存在 u0∈K＼｛θ｝,使得

u-Tu≠τ u0, u∈K∩?Ω, τ≥0,則不動點指數i（T,K∩Ω,K）＝0.

（ii） 若 u≠τ Tu,u∈K∩?Ω,τ≥1,則不動點指數 i（T,K∩Ω,K） ＝1.

本文的工作空間是 X:＝｛u∈C［0,1］:u（0）＝u′（0） ＝u″（1） ＝0｝,其在范數下構成 Banach空間.對于?r＞0,令 Br＝｛u∈C［0,1］:‖u‖ ＜r｝,?Br＝｛u∈C［0,1］:‖u‖ ＝r｝.定義X 中的錐 K ＝｛u∈X:u（t）≥0,t∈［0,1］｝,顯然 K為X中的非負錐.為了得到更好的結果,對于?0＜τ＜1,定義如下的錐

2 主要結果及證明

［1］ Gregu? M.Third Order Linear Differential Equations［M］.Dordrecht:D Reidel Publishing Co,1987.

［2］ Cabada A.The method of lower and upper solution for third-order periodic boundary value problem ［J］.J Math Anal Appl,1995,195:568-589.

［3］ Cabada A.The method of lower and upper solution for second,thrid,fourth,and higher order boundary value problem ［J］.J Math Anal Appl,1994,185:302-320.

［4］ Agarwal R P,Bohner M,Wong P J Y.Positive solution and eigenvalues of conjugate boundary value problem ［J］.Proc Edinburgh Math Soc,1999,42:349-374.

［5］ Grossinho M R,Minhó s F.Existence result for some third order separated boundary value problems ［J］.Nonlinear Anal,2001,47:2407-2418.

［6］ Cabada A,Lois S.Existence of solution for discontinuous third order boundary value problems ［J］.J Comput Appl Math,1999,110:105-114.

［7］ Yao Q L.Successive iteration of positive solution for a discontinuous third-order boundary value problem ［J］.Comput Math Appl,2007,53:741-749.

［8］Cabada A,Heikkil¨a S.Extremality and comparison results for discontinuous third order functional initial-boundary value problems［J］.J Math Anal Appl,2001,255:195-212.

［9］ Jackson L K.Existence and uniqueness of solutions of boundary value problems for third order differential equations ［J］.J Diff Eqns,1993,13:432-437.

［10］ Li S H.Positive solutions of nonlinear singular thrid-order two-point boundary value problem ［J］.J Math Anal Appl,2006,323:413-425.

［11］ Liu Z Q,Sheok J U,Kang S M.Positive solutions of a singular nonlinear third order two-point boundary value problem［J］.J Math Anal Appl,2007,326:589-601.

［12］ Erbe L.Eigenvalue criteria for existence of positive solutions to nonlinear boundary value problems ［J］.Math Comput Model,2000,32:529-539.

［13］郭大鈞.非線性泛函分析［M］.2版.濟南:山東科學技術出版社,2001.

［14］ Zhang G W,Sun J X.Positive solutions of m-point boundary value problems［J］.J Math Anal Appl,2004,291:406-418.

［15］孫彥,劉立山.三階奇異邊值問題的正解［J］.應用數學學報,2009,23（1）:50-58.

［16］張立新.三階邊值問題的3個正解的存在性［J］.四川師范大學學報:自然科學版,2011,34（4）:466-470.

［17］ Ma R Y,Yang Y R.Existence result for s singular nonlinear boundary value problem at resonance ［J］.Nonlinear Anal,2008,66:671-680.

［18］劉興元.具p-laplacian算子方程多點邊值問題3個正解的存在性［J］.四川師范大學學報:自然科學版,2012,35（1）:78-81.

［19］馬如云.二階奇異邊值問題的正解［J］.數學學報,1998,41（6）:1225-1230.

［20］ Asakawa H.Nonresonant singular two-point boundary value problems［J］.Nonlinear Anal,2001,44 （6）:791-809.

［21］ Yao Q L.Positive solutions and eigenvalue intervals of a singular third-order boundary value problem［J］.Ann Polon Math,2011,102（1）:25-37.

［22］ Yao Q L.Solvability of third-order three-point boundary value problems with Carathé odory nonlinearity［J］.Commun Math Res,2012,28（3）:209-217.

［23］王彥,姜杰,裴銀淑.一類三階微分方程的奇異非線性邊值問題［J］.吉林大學學報:理學版,2003,41（3）:280-283.

［24］ Sun J P,Guo L J,Peng J G.Multiple nondecreasing positive solutions for a singular third-order three-point BVP［J］.Commun Appl Anal,2008,12（1）:91-100.

［25］ Hu L G.Positive solutions to singular third-order three-point boundary value problems on time scales［J］.Math Comput Model,2010,51（5）:606-615.

［26］ Feng X F,Feng H Y,Bai D L.Eigenvalue for a singular third-order three-point boundary value problem［J］.Appl Math Comput,2013,219（18）:9783-9790.

［27］ Liu Z S,Chen H B,Liu C.Positive solutions for singular third-order nonhomogeneous boundary value problems［J］.J Appl Math Comput,2012,38（1/2）:161-172.