一類廣義分式規劃的最優性條件和對偶

張彩芬, 吳澤忠

（成都信息工程學院 應用數學學院,四川成都610225）

設Rn表示n維空間,Rn+表示它的非負象限.文獻［1］考慮了如下規劃:

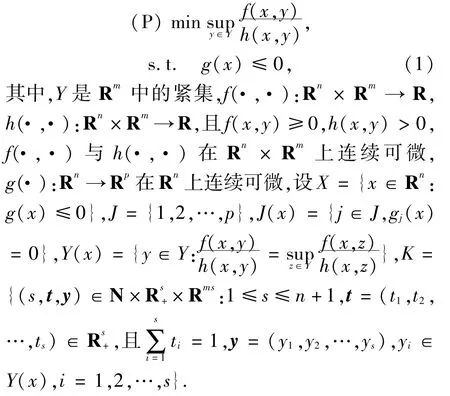
很多學者運用函數的凸性對分式規劃做了相關的研究,文獻［2-4］分別在不變凸性、（F,ρ）-凸性和（F,α,ρ,d） -凸性的假設下,擴展了文獻［1］ 的結果,得到規劃（P）的對偶規劃及其各自的弱對偶、強對偶、嚴格逆對偶定理；文獻［5-10］對可微廣義分式規劃做類似的研究并得出相應的結論；文獻［11-14］對非可微廣義分式規劃及其對偶模型做了研究；文獻［15-17］運用函數的凸性對多目標分式規劃及對偶做相關的研究.本文將在廣義ρ-不變凸性的假設下,得到（P）的2個對偶規劃及其各自的弱對偶、強對偶和嚴格逆對偶定理.

1 預備知識

定義 1.1［18］令f:X→R（X?Rn） 是可微函數,ρ∈R,d:X ×X→R（x1≠x2,d（x1,x2）≠0）,η:X×X→Rn.

（a） 若對 ?x ∈ X 都有 f（x） -f（x0） ≥▽f（x0）Tη（x,x0） +ρd2（x,x0）,則f在x0處是ρ -不變凸函數；

（b） 若對?x∈X,x≠x0,都有f（x）-f（x0） ＞▽f（x0）Tη（x,x0） +ρd2（x,x0）,則f在x0處是嚴格ρ-不變凸函數；

（c） 若對 ?x∈ X,都有 ▽f（x0）Tη（x,x0） ≥-ρd2（x,x0） → f（x） ≥ f（x0） 或 f（x） ＜ f（x0） →▽f（x0）Tη（x,x0） ＜-ρd2（x,x0）；則f在x0處是ρ -偽不變凸函數；

（d） 若對 ?x∈ X,x≠ x0,都有 ▽f（x0）Tη（x,x0） ≥-ρd2（x,x0） →f（x） ＞f（x0） 或f（x） ≤f（x0）→ ▽f（x0）Tη（x,x0） ＜-ρd2（x,x0）；則 f在 x0處是嚴格ρ-偽不變凸函數；

（e） 若對 ?x ∈ X 都有 f（x） ≤ f（x0） →▽f（x0）Tη（x,x0） ≤-ρd2（x,x0）,則f在x0處是ρ -擬不變凸函數.

2 充分條件

3 對偶定理

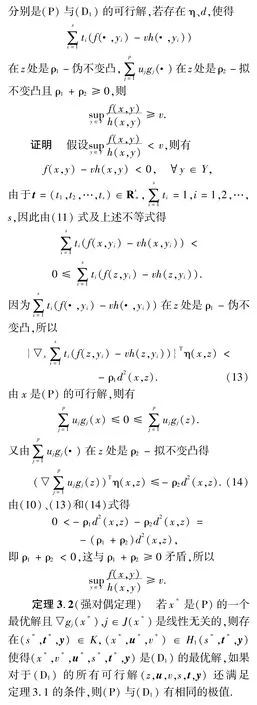
3 結語

在廣義ρ-不變凸性的假設下,得到廣義分式規劃的最優性的充分條件并得到2個對偶規劃的弱對偶、強對偶、嚴格逆對偶定理.廣義分式規劃在不同凸函數的基礎上,已有很多的研究成果,更有待進一步去研究.ρ-不變凸性也可以運用于研究多目標分式規劃.

致謝成都信息工程學院2012年中青年學術帶頭人基金（J201218）和成都信息工程學院2012年人才引進基金（KYTZ201203）對本文給予了資助,謹致謝意.

［1］ Chandra S,Kumar V.Duality in fractional minimax programming［J］.J Austral Math Soc,1995,A58:376-386.

［2］ Liu J C,Wu C S.On minimax fractional optimality conditions with invexity［J］.J Math Anal Appl,1998,219:21-35.

［3］ Liu J C,Wu C S.On minimax optimality conditions with （F, ρ） -convexity［J］.J Math Anal Appl,1998,219:36-51.

［4］ Liang Z A,Shi Z W.Optimality conditiongs and duality for a minimax fractional with generalized convexity ［J］.J Math Anal Appl,2003,277:474-488.

［5］王興國.（F,ρ）-不變凸性下廣義分式規劃的最優性條件［J］.四川師范大學學報:自然科學版,2005,28（1）:66-69.

［6］王興國.廣義分式規劃的混合型對偶［J］.浙江師范大學學報:自然科學版,2001,24（4）:332-336.

［7］王興國.廣義分式規劃的一個混合型對偶［J］.曲阜師范大學學報:自然科學版,2002,28（2）:41-45.

［8］ Antczak T.Generalized fractional minimax programming with B-（F, ρ）-invexity［J］.Comput Math Appl,2008,56:1505-1525.

［9］ Ahmad I,Husain Z.Optimality conditions and duality in nondifferentiable minimax fractional programming with generalized convexity［J］.J Theory Appl,2006,129:255-275.

［10］焦合華.B-（F,ρ）-不變凸規劃的最優性條件及混合型對偶［J］.數學的實踐與認識,2010,40（16）:138-143.

［11］ 袁德輝,龔海林.（C,α,ρ,d）凸極大極小分式規劃的最優性條件［J］.南昌大學學報:理科版,2006,30（2）:127-129.

［12］王興國.一類不可微廣義分式規劃的最優性條件［J］.長春大學學報:自然科學版,2009,19（8）:65-69.

［13］羅和治,吳惠仙,朱藝華.一類非可微廣義分式規劃的混合型對偶［J］.浙江工業大學學報:自然科學版,2003,31（2）:182-186.

［14］羅和治.一類非可微廣義分式規劃的最優性必要條件［J］.浙江師范大學學報:自然科學版,2001,24（3）:239-243.

［15］吳澤忠,鄭豐華.一類非線性分式規劃問題的最優性條件和對偶［J］.四川師范大學學報:自然科學版,2007,30（5）:594-597.

［16］李向有,張慶祥,苗紅梅,等.不變凸多目標分式規劃的最優性［J］.延安大學學報:自然科學版,2009,28（2）:18-20.

［17］羅勇,姚元金.G-（F,ρ）凸性下的非光滑多目標分式規劃的最優性條件［J］.延安大學學報:自然科學版,2010,29（4）:3-6.

［18］ Zalmai G J,Zhang Q H.Parametric duality models for semi-infinite discrete minmax fractional programming problems involving generalized （η,ρ） -invex functions［J］.Acta Math Appl Sinica,2007,23:353-376.