一類具時滯高階泛函微分方程的周期解

汪小明

（上饒師范學院 數學與計算機科學學院,江西 上饒334001）

1 預備知識

隨著微分方程應用的不斷推廣及理論研究的逐漸深入,近年來人們對時滯微分方程的研究非常活躍［1-2］,特別是關于時滯微分方程周期解的存在性研究,受到很多數學研究工作者的重視,并出現了許多較好的研究成果［3-15］.如文獻［8］研究一類Rayleigh方程

2π周期解的存在性；隨后,文獻［10］進一步研究了方程（1）,改進文獻［8］的相關結果.他們都采用重合度理論獲得了很好的結果.本文將上述方法加以拓廣,利用重合度理論和一些不等式分析技巧,討論一類具有時滯的2n階微分方程

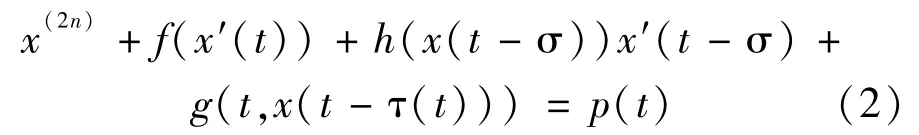
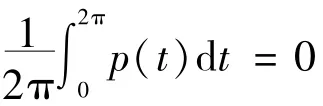
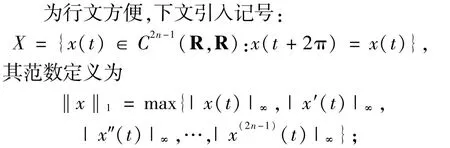
2 主要結果與證明

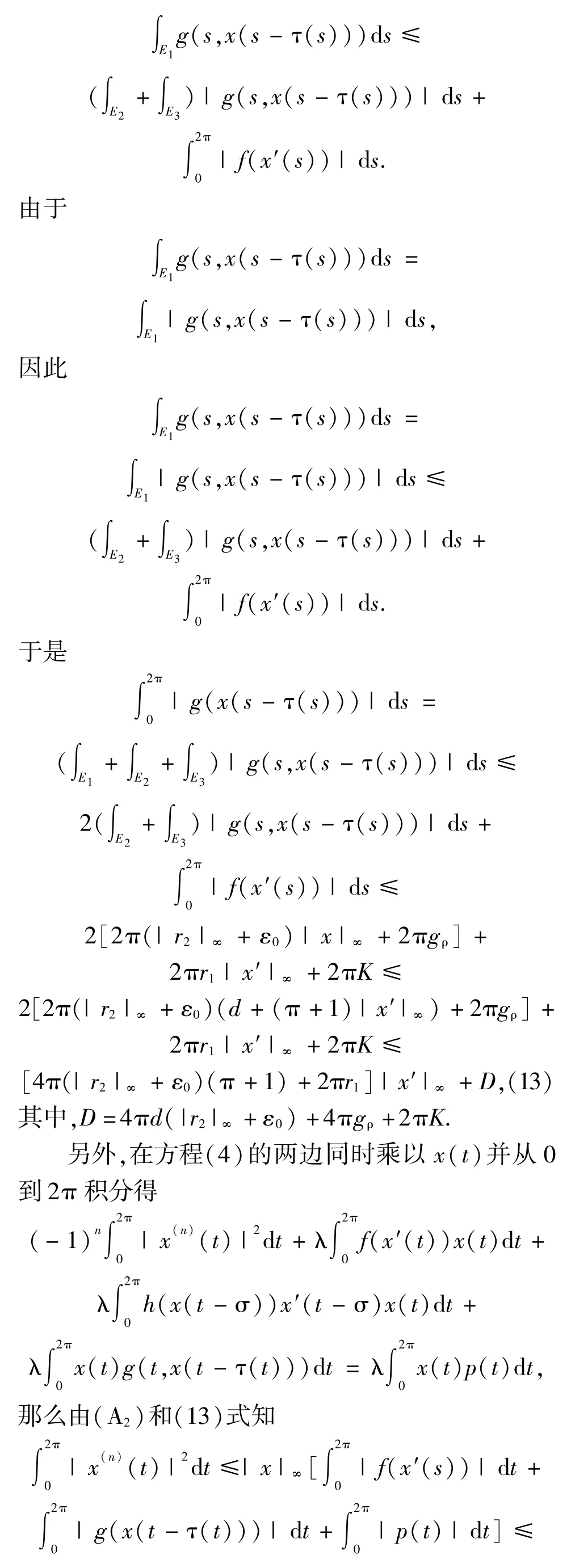
3 舉例

［1］汪媛媛,李永祥.四階時滯微分方程邊值問題的正解［J］.四川師范大學學報:自然科學版,2014,37（2）:172-177.

［2］劉興元.具有正負系數中立型時滯微分方程的振動性［J］.四川師范大學學報:自然科學版,2006,29（2）:192-196.

［3］ 黃先開,向子貴.具有時滯的 Duffing型方程 x″（t） +g（x（t-τ）） ＝p（t）的周期解［J］.科學通報,1994,39（3）:201-203.

［4］張正球,庾建設.一類時滯 Duffing型方程的周期解［J］.高校應用數學學報,1998,A13（4）:389-392.

［5］李永昆.時滯 Duffing型系統的2π周期解［J］.純粹數學與應用數學,1998,14（2）:23-27.

［6］ 黃先開,陳文燈.具有時滯的 Duffing方程 x″+cx′+g（x（t-τ）） ＝p（t） 的2π周期解［J］.自然科學進展,1998,8（1）:118-121.

［7］林壯鵬,徐遠通,郭志明.一類有偏差變元的泛函微分方程的2π周期解［J］.高校應用數學學報,2000,15（4）:421-427.

［8］ Wang G G,Cheng S S.A priori bounds for periodic solutions of a delay Rayleigh equation ［J］.Appl Math Comput,1999,12（3）:41-44.

［9］ 彭世國.時滯 Lié nard 型方程的周期解［J］.工程數學學報,2004,21（3）:463-466.

［10］魯世平,葛渭高,鄭祖庥.具偏差變元的 Rayleigh方程周期解問題［J］.數學學報,2004,47（2）:209-304.

［11］鄧偉,蒲志林.一類中立型Duffing方程的周期解［J］.四川師范大學學報:自然科學版,2012,35（5）:585-588.

［12］汪小明.一類具多個偏差變元Rayleigh型p-Laplacian方程周期解［J］.數學研究,2012,45（2）:115-123.

［13］ Wang X M.On the existence of periodic solutions for a class of Rayleigh type p-Laplacian equations with deviating arguments［J］.Nonlinear Oscillations,2012,15（3）:331-336.

［14］汪小明.偏差變元的混合型p-Laplacian方程的周期解［J］.數學季刊,2012,27（2）:177-182.

［15］汪小明.具偏差變元高階Rayleigh型方程周期解的存在性［J］.南昌大學學報:理科版,2014,38（2）:128-131.

［16］ Gaines R E,Mawhin J L.Coincidence Degree and Nonlinear Differential Equations［M］.Berlin:Springer-Verlag,1977.