基于MATLAB的井下碎石車垂直工作范圍求解
耿曉光,李葉林,馬 威,王順凱
GENG Xiao-guang,LI Ye-lin,MA Wei,WANG Shun-kai
(北京科技大學 機械工程學院,北京 100083)
0 引言
井下碎石車以其安全性好、效率高、成本低等優點已取代爆破法和人工大錘法而成為井下礦山開采二次破碎的重要設備。其一次定位的工作范圍(一般指垂直破碎范圍)作為一個重要的參數和技術指標,對實際作業有很強的指導意義,能夠有效的提高工作效率和質量,所以對它的研究很有必要。
碎石車的機械臂是一種開環的空間多連桿機構,由一系列連桿通過轉動關節串聯而成,通過連桿的配合動作使破碎錘釬桿達到不同的空間位姿。本文通過理論分析,并借助MATLAB軟件編程實現曲線的繪制,得到正確的工作范圍,給碎石車的作業帶來指導,給其他相關方面的研究提供了思路和想法。
1 機械臂結構
使用SolidWorks軟件對機械臂進行三維建模,其結構如圖1所示。各構件之間全部采用鉸接連接,在液壓缸的作用下各部件繞鉸接點擺動。
2 簡化模型和幾何分析
分析之前需要對原有的三維模型進行簡化,將機械臂的各個部分視為桿件,通過關節相連,在油缸的作用下實現動作。進而進行幾何分析,找到在油缸安裝距確定的情況下,機械臂擺動角度隨油缸行程變化的對應關系。

圖1 機械臂結構
1)內臂部分
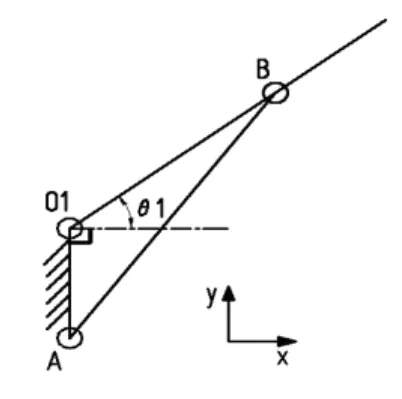
圖2 內臂機構簡圖
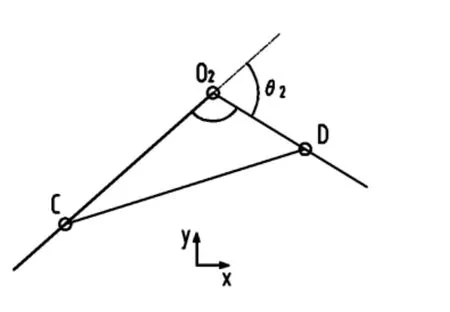
圖3 外臂機構簡圖
內臂的機構簡圖如圖2所示,其中A、B為舉臂油缸的兩個鉸接點,O1為內臂的轉軸。在△AO1B中由余弦定理可求得:

內臂轉角θ1(相對于水平面)可求:
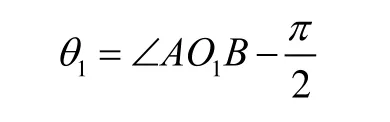
除了油缸長度LAB和內臂轉角θ1,其他都是已知量,且為定值,這樣就得到了兩者的一一對應關系。
2)外臂部分
外臂的機構簡圖如圖3所示,C、D分別為折疊油缸的兩個鉸接點,O2為外臂的轉軸。同內臂的求解方法:

內臂轉角θ2=π? ∠C O2D 。
3)破碎錘部分
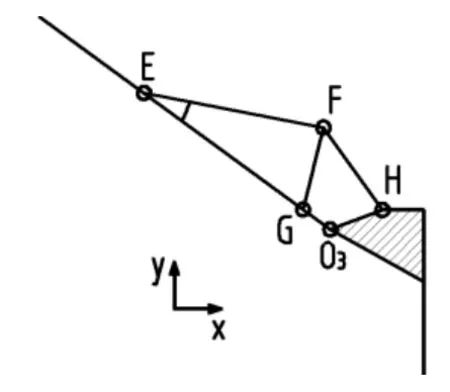
圖4 破碎錘機構簡圖1

圖5 破碎錘機構簡圖2
破碎錘部分的結構簡圖如圖4所示,其中E、F為轉錘油缸的兩個鉸接點,O3為轉錘的轉軸,此處,油缸通過四連桿機構間接作用于轉錘,而FG相當于四連桿機構的搖桿。在△FEG中由余弦定理可求得:

此處結構繼續進行簡化,如圖5所示。
θ3為破碎錘轉角,可由∠FEG間接求得。此處采用四連桿機構起到運動放大和防干涉作用。
通過以上分析,得到了油缸行程和各機械臂轉角的對應關系。只要確定油缸安裝距和行程等尺寸參數就可以計算出機械臂各關節的轉角范圍,為后續應用D-H法求解正向運動學方程打好了基礎。
3 建立運動學方程
碎石車機械臂是一種典型的多關節機器手臂,其工作范圍即破碎錘釬桿所能達到的范圍,此處采用機器人D-H法可以很好的解決。

圖6 機械臂的參考坐標系線圖
首先,如圖6所示,根據D-H法將機械臂簡化為連桿和關節模型,并確定各個關節的參考坐標系。由于各桿件均在一個平面內,z軸均垂直于紙面且平行,所以距離d和角α均為0,θ是桿件繞z軸旋轉的角度(即各臂的轉角,且順時針為負,逆時針為正),l表示各臂的長度。其中θ1、θ2、θ3已經分析求得,為定值,各參數如表1所示。

表1 D-H參數表
為求出碎石車垂直工作范圍,θ1和θ2可在各自范圍內任意取值,θ3不僅需在范圍內取值外,還需要和θ1、θ2滿足一定的關系:θ3=-θ1-θ2。從而保證l3始終保持水平(θ4=-90o,l4即可保持豎直)。
然后,從基座到第一關節,再從第一關節到第二關節直至到最后一個關節進行坐標的變換,如此下去就得到了破碎錘釬桿相對于基坐標系的位置和姿態。
變換矩陣可表示為:

其中s θ表示sin θ,c θ表示cos θ。
因此,破碎錘釬桿相對于底座的位置變換矩陣為:
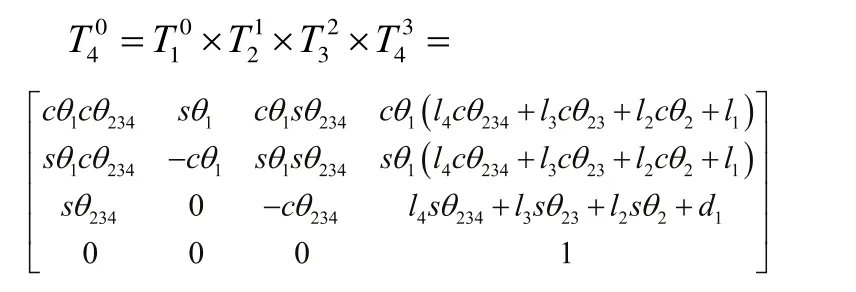
式 中 cθ23= cos(θ2+θ3),sθ23= sin(θ2+ θ3),θ234= θ2+ θ3+ θ4,其余類推。
矩陣 T40最后一列即為破碎錘釬桿的位置坐標,且已知z=0,故有:
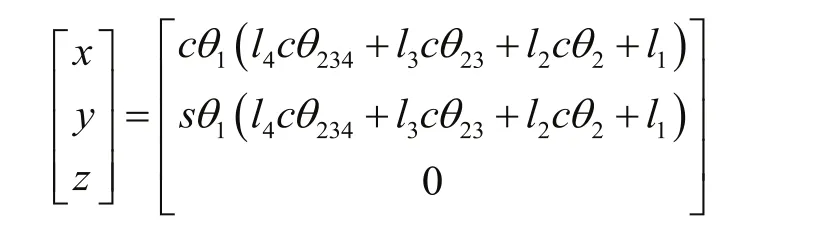
因為l1、l2、l3和l4均為已知,所以問題就轉化為破碎錘釬桿位置坐標和機械臂擺角的對應函數關系,下面借助MATLAB軟件即可實現求解,并且輸出工作范圍曲線。
4 MATLAB繪制工作范圍
根據上述由D-H法建立的正向運動學方程,通過MATLAB編程實現,即可繪制出破碎車的工作范圍,如圖7所示。
5 結論
1)通過MATLAB軟件仿真得到工作范圍,對井下實際的生產作業有很好的指導價值。
2)這種方法簡便易懂,對于正向運動學問題的解決有較高的可靠性和可操作性。

圖7 碎石車垂直工作范圍
3)工作范圍的求解可以反過來指導破碎車機械臂的設計。
[1]劉澤鑫,管會生.鑿巖臺車鉆臂工作空間求解[J].機械,2012(5).
[2]趙強,吳洪濤,朱劍英.車載起重機械吊臂工作范圍的研究[J].機械科學與技術,2005,12:1460-1462-1506.
[3]趙亮亮,馬振書,杜峰坡.基于ADAMS的危險作業機械手工作軌跡分析[J].機械與電子,2011(1),44-47.
[4]周芳芳,樊曉平,葉榛.D-H參數表生成三維機器人模型仿真系統[J].系統仿真學報,2006,04:947-950.
[5]孫祥,徐流美,吳清.MATLAB7_0基礎教程[M].北京:清華大學出版社,2005.

