指數分布族的一致最優檢驗及樣本容量的確定

趙麗棉，黃基廷

(河池學院 數學與統計學院，廣西 宜州 546300)

0 引言

設X=(X1，…，Xn)是從總體{Fθ(x)，θ∈Θ}中抽取的簡單樣本，其中Θ為參數空間，檢驗問題為H0∶θ∈Θ0?H1∶θ∈Θ1=Θ－Θ0.我們通過一個統計量在一個子樣中的觀察值來檢驗H0，則當觀察到點X屬于拒絕域 W 時，拒絕假設H0，否則接受H0，稱稱為非隨機化檢驗。在實際問題中，有些檢驗函數φ(x)除了0，1外還能取(0，1)內的值，如設X=(X1，…，Xn)是從一大批產品中抽得的樣本，記G(X)為其中的次品數，當G(X)＜c時認為這批產品合格;當G(X)＞c時認為不合格;而當G(X)=c時可以定下(0，1)內的一個數r，作一次成功概率為r的隨機試驗，根據試驗結果來決定這批產品是否合格，這種檢驗稱為隨機化檢驗。由于子樣觀察值的出現帶有隨機性，因此判斷會發生兩種錯誤:第一，假設H0本來是對的，但由于觀察值落入拒絕域W，錯誤地將H0否定了，這時犯的錯誤稱為第一類錯誤;第二，假設H0本來是不對的，但由于觀察值落入接受域，錯誤地將H0接受了，這時犯的錯誤稱為第二類錯誤。一個好的檢驗當然是使犯兩種錯誤的概率盡可能小，最好全為零，但實際上這是不可能的，通常只能通過限制第一類錯誤的概率使第二類錯誤的概率達到最小。用βφ(θ)=Pθ{用檢驗φ否定了H0}=Eθ[φ(X)](θ∈Θ)表示 φ(x)的功效函數，則當 θ∈Θ0時，βφ(θ)是犯第一類錯誤的概率;θ∈Θ1時，1 － βφ(θ)是犯第二類錯誤的概率。我們要做的是在 Eθ[φ(X)]≤α，θ∈Θ0的條件下，使 βφ(θ)，θ∈Θ1達到最大值。這種檢驗稱為水平為α的一致最優檢驗(簡稱UMP檢驗)。UMP檢驗不一定存在，但對相當廣泛的指數分布族卻能找出這種檢驗來。為檢驗函數，這里φ(x)只取0，1兩個值，這種檢驗

1 指數分布族的UMP檢驗的存在性

定義:設{f(x，θ)∶θ∈Θ}是定義在樣本空間R上的分布族，其中Θ為參數空間。若其概率密度函數f(x，θ)可表示成如下形式:

其中，k為自然數，C(θ)＞0和 Qi(θ)(i=1，2，…，k)都是定義在 Θ 上的函數，h(x)＞0和 Ti(x)(i=1，2，…，k)都是定義在R上的函數，則稱此分布族為指數分布族。

NP基本引理:設樣本X有概率函數f(x，θ)，參數θ只有兩個可能的值θ0和θ1，檢驗問題為:

則存在非負常數c和0≤r≤1，使得檢驗問題(1)的水平為α的一致最優檢驗函數為:

證明參見文獻[1]。

定理:設樣本X=(X1，…，Xn)的分布為指數分布族:

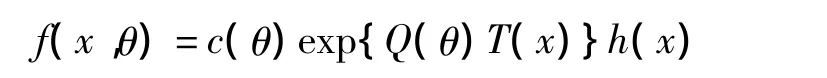
其中c(θ)，Q(θ)為θ的函數且c(θ)＞0，T(x)和h(x)是樣本x的函數。參數空間Θ為R1的子集，θ0為Θ的一個內點且Q(θ)為θ的嚴格增函數，則檢驗問題:

的水平為α的一致最優檢驗存在，且具有形式:

其中 c和 r(0≤r≤1)滿足條件 Eθ0[φ(X)]=α.

證:①先考慮檢驗問題:

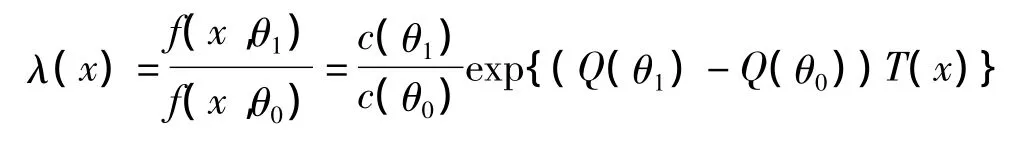
易知λ(x)是T(x)的嚴格增函數，由引理知檢驗問題(5)的一致最優檢驗函數為(4)式，其中c和r滿足:

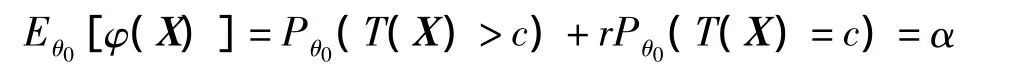
由于c和r與θ1無關，所以(4)式確定的φ(x)也是檢驗問題:

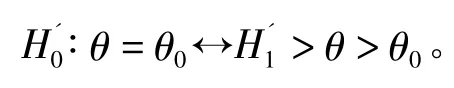
的水平為α的一致最優檢驗。

②證由(4)式確定的φ(x)也是檢驗問題(3)的水平為α的檢驗，即證

當 θ≤θ0時，

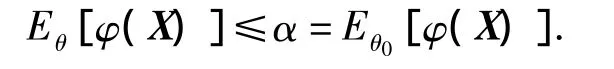
對任意的 θ≤θ0，顯然

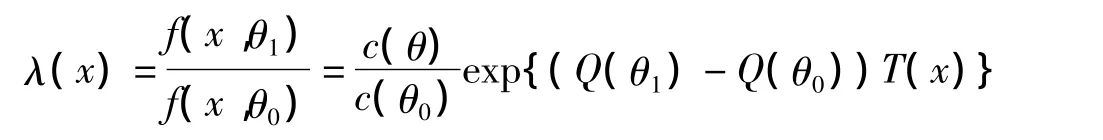
似然比

是T(x)的嚴格減函數。由

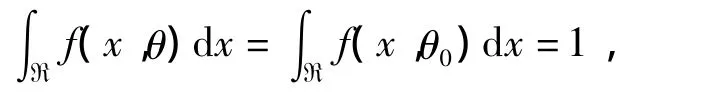
其中R為樣本空間知，存在t0使

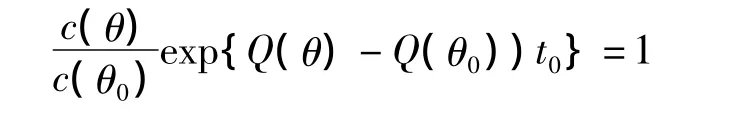
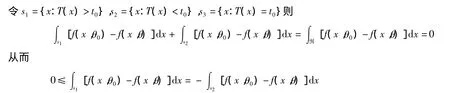
由(4)式知φ(x)只與T(x)有關，且是T(x)的非降函數，故有

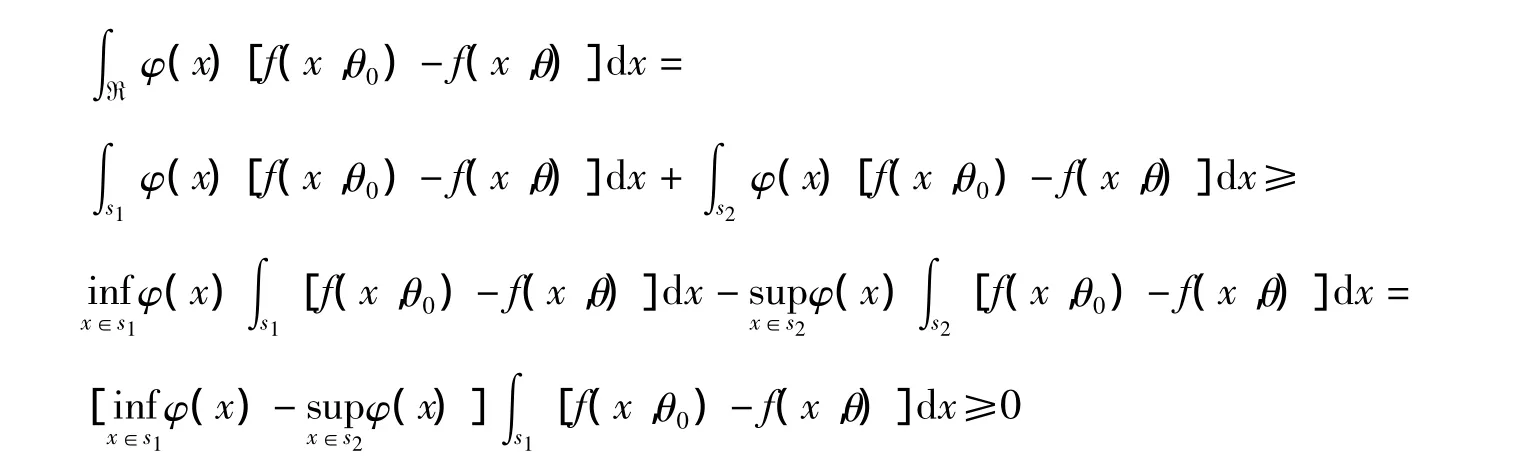
2 確定指數分布族的UMP檢驗的方法步驟

由定理可知UMP檢驗函數φ(x)主要由r和c確定，所以確定指數分布族的UMP檢驗的步驟可分為以下幾步:

(1)寫出樣本 X=(X1，…，Xn)的密度:f(x，θ)=c(θ)exp{Q(θ)T(x)}h(x)，并確定統計量 T(X)的分布;

(2)由 Eθ0[φ(X)]=α 即 Pθ0(T(X)＞c)+rPθ0(T(X)=c)=α 確定 r;

(3)由0≤r≤1及T(X)的分布確定c.

注:當總體為連續分布時，由于 Pθ0(T(X)=c)=0，所以直接由 Eθ0[φ(X)]=Pθ0(T(X)＞ c)= α 及統計量T(x)的分布即可確定c.此時

3 常見分布的UMP檢驗

不難看出，統計上常用的正態分布族、二項分布族、Poisson分布族等都是指數分布族，它們的一致最優檢驗都是存在的。

例1:設X1，…，Xn是從分布為Fθ的總體中抽取的簡單樣本，其中θ為未知參數。求檢驗問題H0∶θ≤θ0?H1∶θ＞θ0)的水平為α的UMP檢驗函數φ(x)，其中θ0，α給定。下面幾種常見分布均滿足定理條件，故它們的UMP檢驗函數φ(x)為(4)或(6)式。

1° 當 Fθ～N(θ，σ2)，σ2已知時

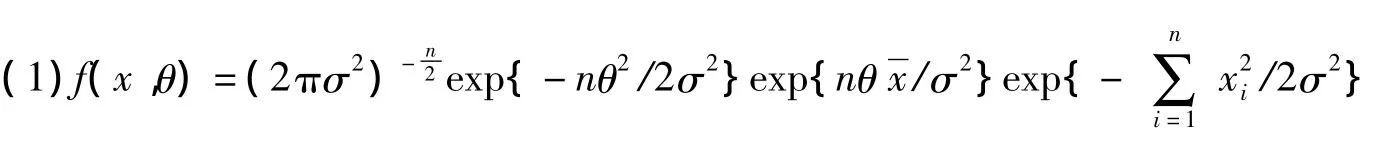
其中

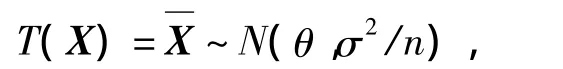
從而

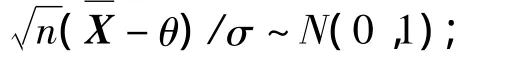
得

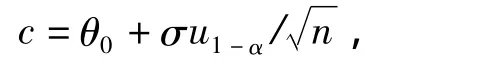
其中Φ(u1－α)=1－α，Φ為標準正態分布函數。UMP檢驗函數φ(x)為(6)式。

2° 當 Fθ～N(a，θ2)，a已知，θ＞0 時

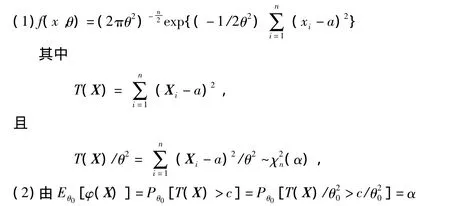
得 c= θ20χ2n(α)，一致最優檢驗函數 φ(x)為 (6)式。3° 當 Fθ為指數分布 θ－1e－x/θ，θ＞0 時

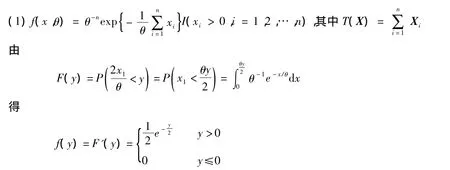
因此f(y)是自由度為2的χ2密度，即分布。再利用分布的可加性知，

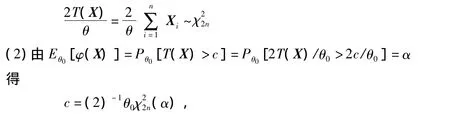
UMP檢驗函數φ(x)為 (6)式。

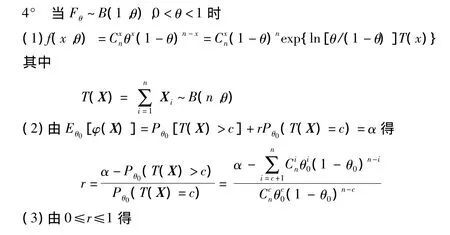
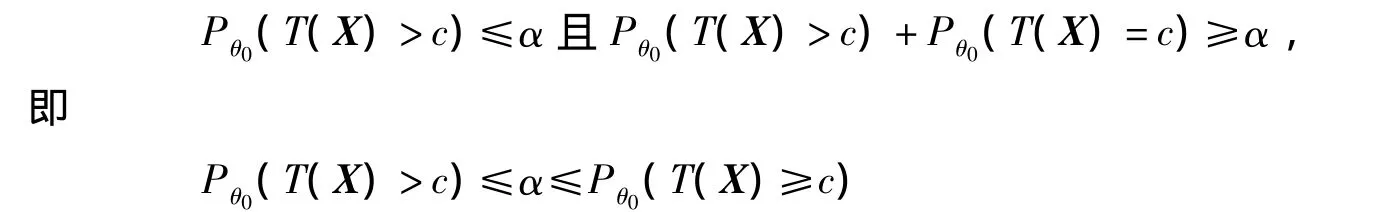
所以c由下列不等式確定:

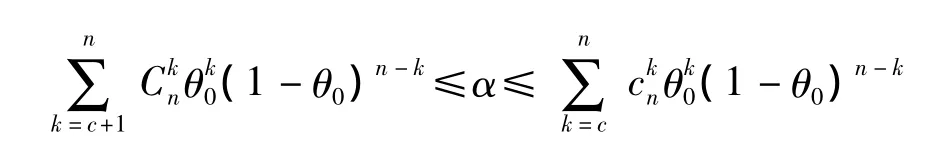
UMP檢驗函數φ(x)為 (4)式。

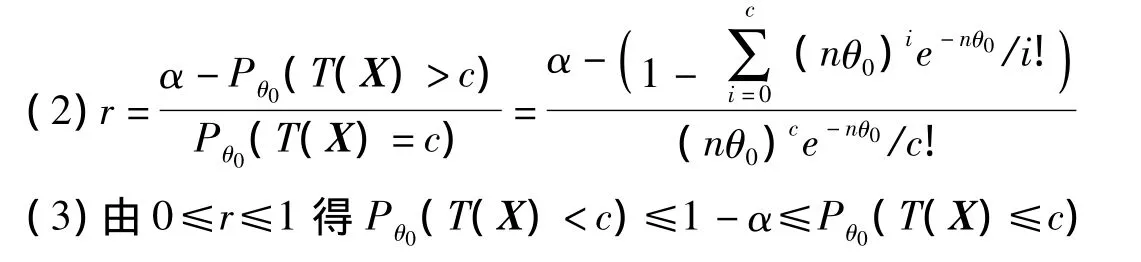
所以c由下列不等式確定:

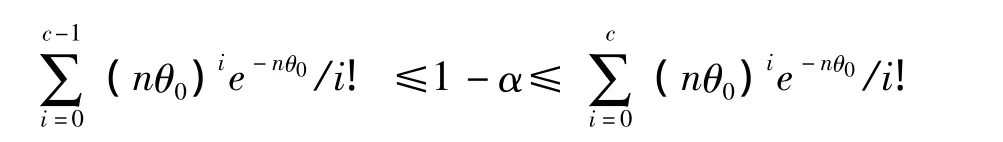
UMP檢驗函數φ(x)為 (4)式。

4 樣本容量的確定

前面討論的問題，都是根據樣本容量及第一類錯誤的概率(即顯著水平)，確定一致最優檢驗使其犯第二類錯誤的概率到最小。在實際應用中，有時會提出檢驗問題(1)，且給出第一、第二類錯誤的概率α、β，要確定樣本容量并找出UMP檢驗。要解決這類問題，可先按前面方法確定最優檢驗函數φ(x)，再由第一、第二類錯誤的概率的定義，聯立關于α、β方程組，從中求出樣本容量及c。下面只舉一例說明解決這類問題的具體方法。

例2:設總體服從正態分布N(θ，σ2)，其中θ為未知參數，σ2為已知。要在第一、第二類錯誤的概率分別為 α、β 條件下用 UMP 檢驗問題 H0∶θ=θ0?H1∶θ=θ1(θ1＞θ0)，樣本容量 n必須多大?

解:由例1知此問題的UMP檢驗函數為:

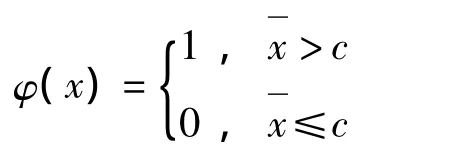
其中當H0為真時);當 H1為真時

依題意得:

[1]韋來生.數理統計[M].北京:科學出版社，2008.

[2](波蘭)M.費史.概率論及數理統計[M].上海:上海科學技術出版社，1978.

[3]復旦大學.概率論(第二冊)數理統計(第二分冊)[M].北京:人民教育出版社，1983.

[4]陳希孺.高等數理統計學[M].合肥:中國科學技術大學出版社，2009.

[5]孫榮恒.應用數理統計[M].北京:科學出版社，2003.