具有脈沖的非線性微分方程邊值問題的多個正解

吳麗嬌，王全義

（華僑大學 數學科學學院，福建 泉州362021）

脈沖微分方程是微分方程中一個新的分支，它在物理、化學、生物醫學、工業機器人技術和經濟學中都有很好的應用.脈沖微分方程邊值問題的正解的存在性問題受到許多學者的廣泛關注［1-10］.例如，文獻［5］運用錐壓縮與不動點定理，研究以下一類具有脈沖的一階微分方程邊值問題

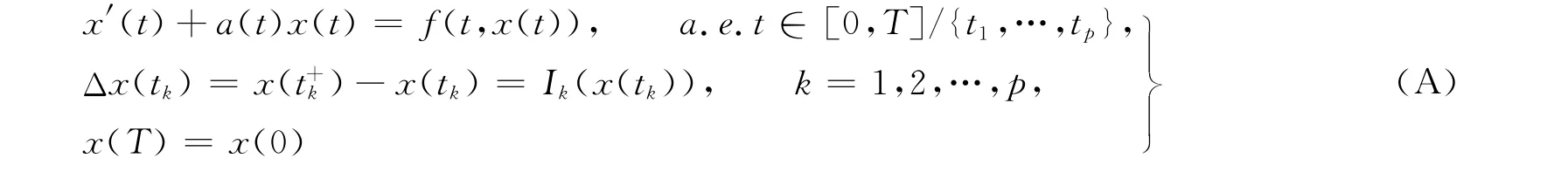
正解的存在性問題.其中：0＝t0＜t1＜…＜tp＜tp+1＝T，f∶［0，T］×［0，+∞）→［0，+∞）是一個脈沖Caratheodory函數，Ik∶［0，+∞）→［0，+∞）是連續的.

文獻［10］運用錐壓縮與不動點定理，研究具有脈沖的一階非線性微分方程邊值問題

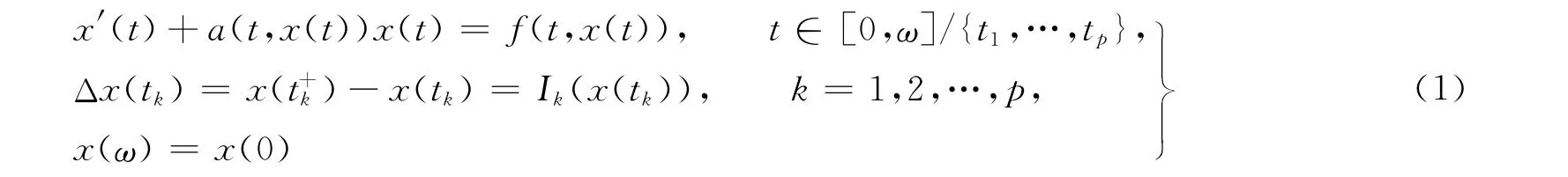
的正解存在性問題.其中：0＝t0＜t1＜…＜tp＜tp+1＝ω；a∶［0，ω］×［0，+∞）→R連續；Ik∶［0，+∞）→［0，+∞）（k＝1，…，p）是連續的；f∶［0，ω］×［0，+∞）→［0，+∞）；ω＞0是常數.所得結果推廣并改進了文獻［5］的相關結果.本文利用Avery-Henderson不動點定理以及一些分析技巧，得出了該脈沖非線性微分方程的邊值問題存在多個正解的一些充分條件的新結果.

1 預備知識及引理

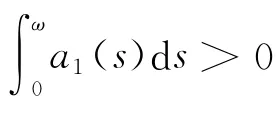
定義1 設X是一個Banach空間，K是X中的一個非空子集，且滿足：1）對任意的x，y∈K和實數α，β≥0，有αx+βy∈K；2）若x，-x∈K，則x＝0.那么稱K為X中的一個錐.

定義2 設X是一個Banach空間，K是X中的一個錐.定義K上的偏序：如果對任意的x，y∈K，x≤y當且僅當y-x∈K.

定義3 設X是一個Banach空間，K是X中的一個錐.如果映射φ∶K→［0，+∞）滿足對任意的x，y∈K，x≤y，就有φ（x）≤φ（y），則稱映射φ是錐K上的一個非負連續的增泛函.

假設φ是錐K上的一個非負連續的增泛函，K?X，?d＞0，記集合K（φ，d）＝｛x∈K｜φ（x）＜d｝；?K（φ，d）＝｛x∈K｜φ（x）＝d｝；K（φ，d）＝｛x∈K｜φ（x）≤d｝.

引理1［11］（Avery-Henderson）設K是X中的一個錐.令γ，φ是K上的非負連續增泛函，θ是K上的非負連續泛函，其中θ（0）＝0.存在常數c＞0和M＞0，對?x∈K（γ，c），使得γ（x）≤θ（x）≤φ（x），‖x‖≤Mγ（x）.假設存在一個全連續算子T∶K（γ，c）→K，對常數0＜a＜b＜c，0＜λ＜1及x∈?K（θ，b）滿足θ（λx）≤λθ（x），且

1）γ（Tx）＞c，當x∈?K（γ，c）時；

2）θ（Tx）＜b，當x∈?K（θ，b）時；

3）φ（Tx）＞a及K（φ，a）≠φ，當x∈?K（φ，a）時，則算子T在K上至少存在兩個不動點x1，x2∈K（γ，c）使得a＜φ（x1），θ（x1）＜b，b＜θ（x2），γ（x2）＜c.

引理2［11］（Avery-Henderson）設K是X中的一個錐.令γ，φ是K上的非負連續增泛函，θ是K上的非負連續泛函，其中θ（0）＝0.存在常數c＞0和M＞0，對?x∈K（γ，c），使得γ（x）≤θ（x）≤φ（x），‖x‖≤Mγ（x）.假設存在一個全連續算子T∶K（γ，c）→K，對常數0＜a＜b＜c，0＜λ＜1及x∈?K（θ，b）滿足θ（λx）≤λθ（x），且

1）γ（Tx）＜c，當x∈?K（γ，c）時；

2）θ（Tx）＞b，當x∈?K（θ，b）時；

3）φ（Tx）＜a及K（φ，a）≠φ，當x∈?K（φ，a）時，則算子T在K上至少存在兩個不動點x1，x2∈K（γ，c）使得a＜φ（x1），θ（x1）＜b，b＜θ（x2），γ（x2）＜c.

下面令

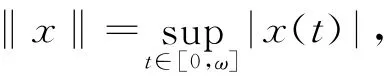
定義4 函數f∶［0，ω］×［0，+∞）→［0，+∞）是一個L1-Caratheodory函數，如果1）對于?u∈R，f（·，u）∈X；2）對于t∈［0，ω］，f（t，·）是連續的；3）對于每個q＞0，都存在hq∈L1［0，ω］，使得對于t∈［0，ω］，0≤u≤q，有｜f（t，u）｜≤hq（t）.

假設條件 H2）函數f∶［0，ω］×［0，+∞）→［0，+∞）是一個L1-Caratheodory函數成立.

引理3［10］如果條件H2）成立，則對于任意的u∈X且u（t）≥0，θk∈R，下列脈沖微分方程的邊值問題

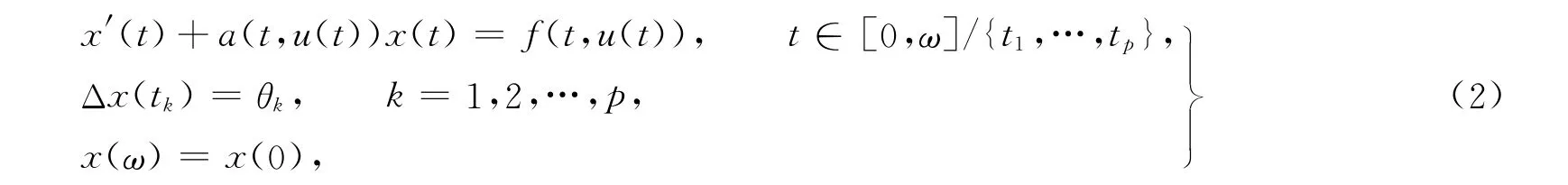
有一個解，即

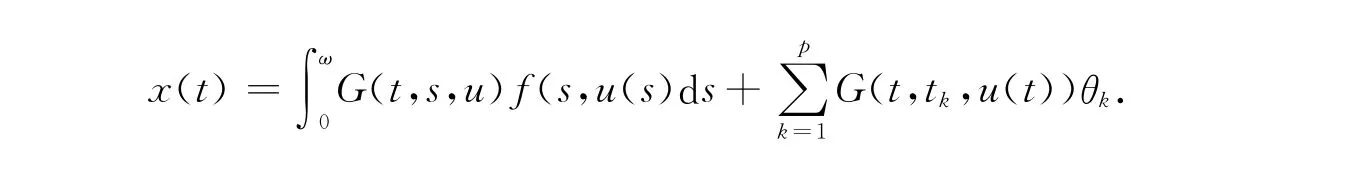
其中

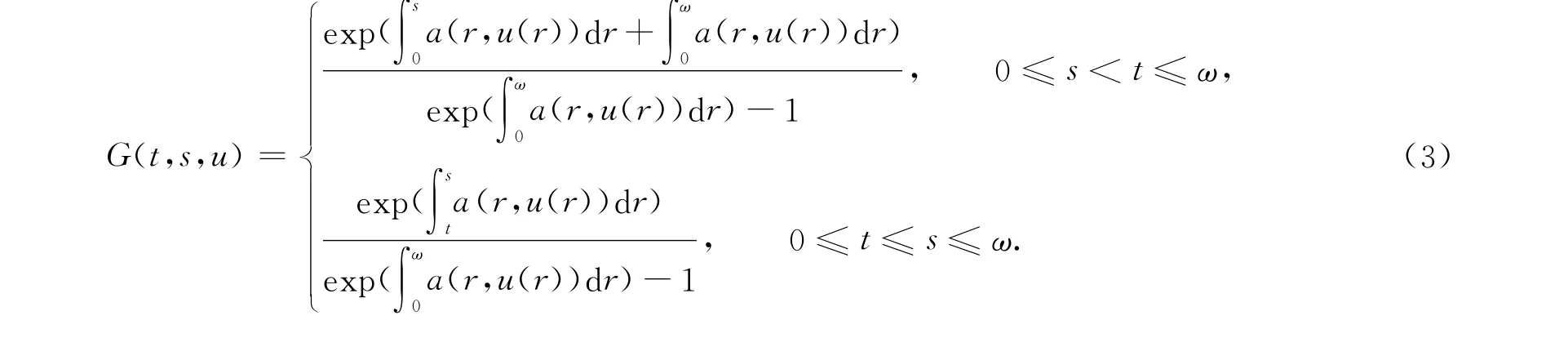
假設函數a1（t），a2（t）滿足條件 H1），現在定義函數

令

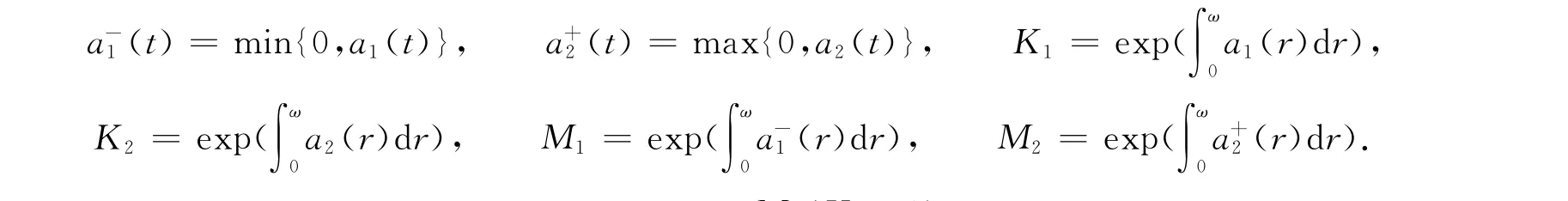
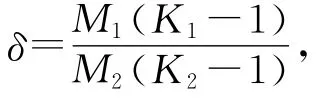
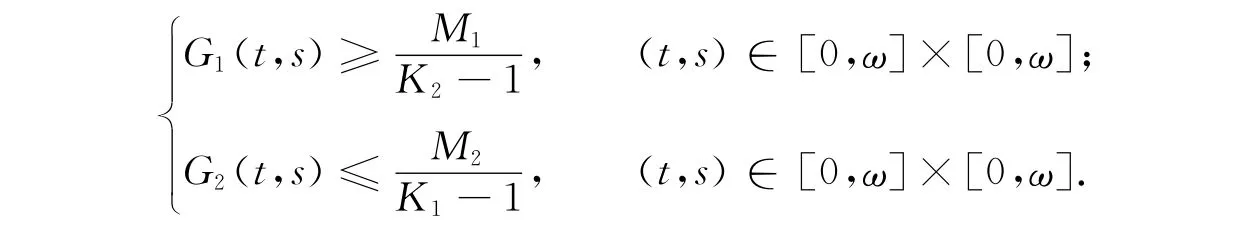
由a1（t），a2（t），a（t，x），G1（t，s），G2（t，s）的定義即得到如下引理4.

引理4 如果條件 H1），H2）成立，則對任意x∈X，（t，s）∈［0，ω］×［0，ω］，有

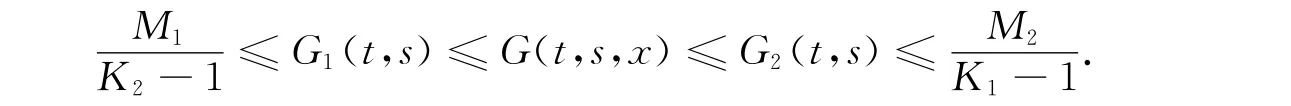
定義算子T∶K→X為

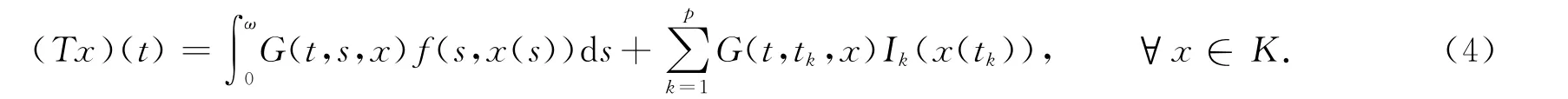
顯然有T∶K→X.

引理5 如果條件H1）成立，則算子T∶K→K.

由于文中的錐K是文獻［10］中的錐K的一個子集，且文中的算子T與文獻［10］中的算子T的表達式相同，故由文獻［10］中的引理6立即得到如下的引理.

引理6 如果條件H1），H2）成立，則算子T∶K→K是全連續的.

2 主要結果及證明

首先，取正數l1，l2滿足0＜l1＜t1＜l2＜t2＜ω，再取下列正數

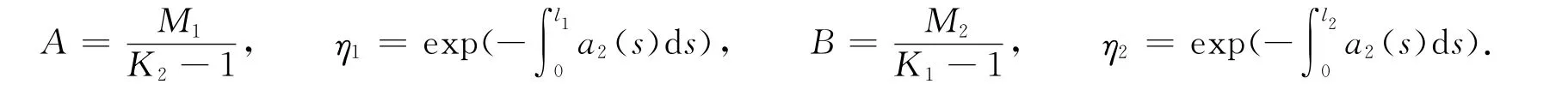
并定義如下一些泛函，即

其中，x∈K.則顯然如下命題成立.

命題1 i）γ，θ，φ是關于x∈K的非負連續增泛函；

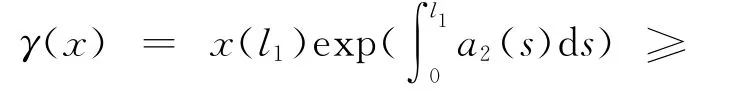
iii）對λ∈［0，1］，有θ（λx）≤θλ（x）.

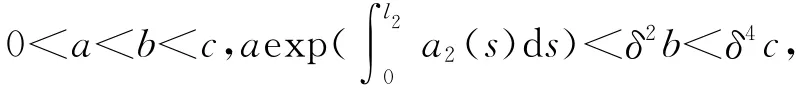
證明 考慮由式（4）定義的算子T∶K→X.由引理5和引理6易知T∶K（γ，c）→K且T是全連續的.再考慮由式（5）～（7）定義的K上的3個非負連續增泛函γ（x），θ（x），φ（x）.

下面證明算子T滿足引理1中的所有條件.

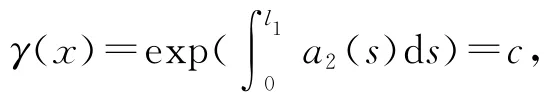
由命題1的結論ii）可知：當x∈?K（γ，c）時，可以得到

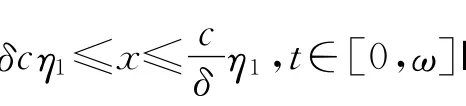
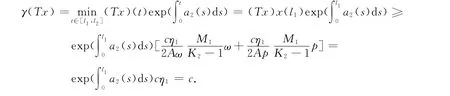
其中，x∈?K（γ，c）.即引理1的條件1被滿足.

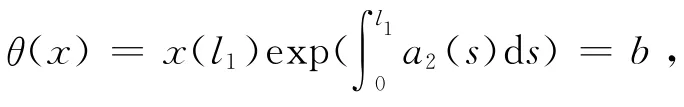
①分娩方式：統計兩組產婦自然分娩率、難產率和剖宮產率。②產程進展：比較兩組產婦第一產程、第二產程時間。③分娩結局：比較兩組產后出血、新生兒窒息、早產、新生兒死亡發生率。其中，產后出血指胎兒娩出后2 h產婦陰道出血量>500 mL；新生兒窒息指新生兒出生后1 min Apgar評分<7分。

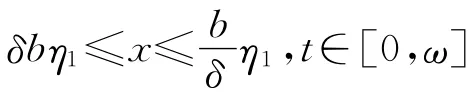
其中，x∈?K（θ，b）.即引理1的條件2被滿足.

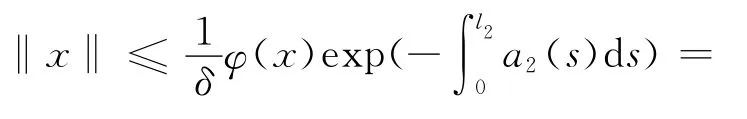
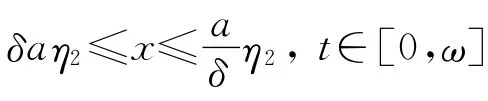
其中，?x∈?K（φ，a）.即引理1的條件3被滿足.

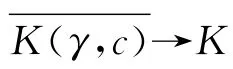
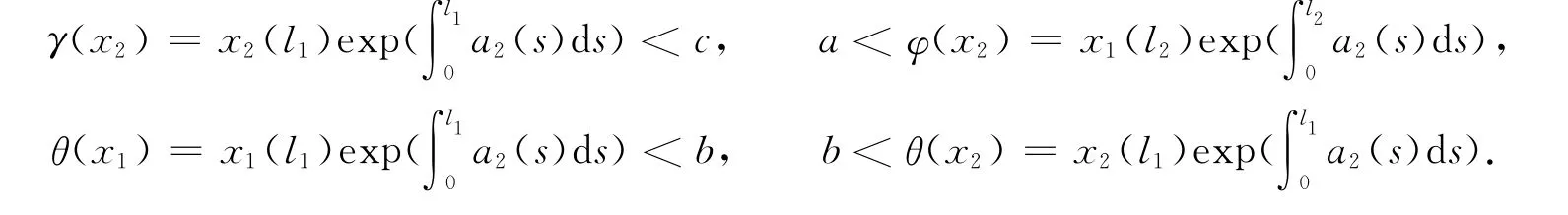
為了得到另一個新結果，取正數l1，l2滿足0＜l1＜t1＜l2＜t2＜ω，并定義如下一些新泛函（為簡單起見，仍然采用前面的符號）.即有

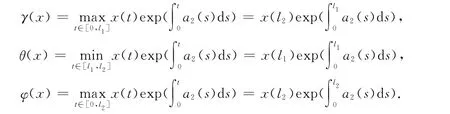
其中，x∈K.則顯然如下命題成立.

命題2 i）γ，θ，φ是關于?x∈K的非負連續增泛函；

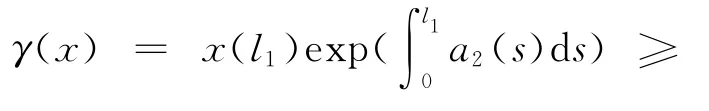
iii）對λ∈［0，1］有θ（λx）≤λθ（x）.

那么脈沖邊值問題（1）至少存在兩個正解x1，x2∈K（γ，c），使得x1（l2）＞aη2，x1（l1）＜bη1，x2（l1）＞bη1，x2（l1）＜cη1（因篇幅限制，證略）.

［1］ NIETO J J.Basic theory for nonresonance impulsive periodic problems of first order［J］.Journal of Mathematical A-nalysis and Applications，1997，205（2）：423-433.

［2］ ZHAO Ai-min，BAI Zhen-guo.Existence of solutions to first-order impulsive periodic boundary value problems［J］.Nonlinear Analysis，2009，71（5／6）：1970-1977.

［3］ NIETO J J.Periodic boundary value problems for first order impulsive ordinary differential equations［J］.Nonlinear Analysis，2002，51（7）：1223-1232.

［4］ LIU Yang-shen.Periodic boundary value problems for first order functional differential equations with impulsive［J］.Journal of Computational and Applied Mathematics，2009，223（1）：27-39.

［5］ LIU Yu-ji.Positive solutions of periodic boundary value problems for nonlinear first-order impulsive differential equations［J］.Nonlinear Analysis，2009，70（5）：2106-2122.

［6］ LI Jian-li，SHEN Jian-hua.New comparison results for impulsive functional differential equations［J］.Applied Mathematics Letters，2010，23（4）：487-493.

［7］ NIETO J J.Impulsive resonance periodic problems of first order［J］.Applied Mathematics Letters，2002，15（4）：489-493.

［8］ ZHANG Feng-qin，MA Zhi-en，YAN Ju-rang.Periodic boundary value problems for first order impulsive delay differential equations with a parameter［J］.Journal of Mathematical Analysis and Applications，2004，290（1）：213-223.

［9］ LI Jian-li，NIETO J J，SHEN Jian-hua.Impulsive periodic boundary value problems of first-order differential equations［J］.Journal of Mathematical Analysis and Applications，2007，325（1）：226-236.

［10］ 吳麗嬌，王全義.具有脈沖的一階非線性微分方程邊值問題的正解［J］.華僑大學學報：自然科學版，2012，33（3）：342-347.

［11］ AVERY R I，HENDERSON J.Two positive fixed points of nonlinear operations on ordered Banach spaces［J］.Comm Appl Nonlinear Anal，2001，8（1）：27-36.