一種四階P－Laplace圖像盲復原方法

劉 琨，王國宇，姬婷婷

（中國海洋大學信息科學與工程學院，山東 青島266100）

圖像在形成、傳輸和存儲過程中不可避免地引起圖像質量的退化，如成像系統的缺陷、外部干擾等等。在成像系統為線性平移不變系統的假定下，可用如下模型來描述退化的圖像［1］：

其中：u（x，y）表示理想圖像；h（x，y）表示成像系統的點擴散函數；n表示圖像的加性噪聲；u0（x，y）為退化模糊圖像；表示卷積操作。

圖像盲復原問題是圖像處理問題中的經典問題之一，近年來圖像盲復原算法得到了廣泛的研究。圖像復原算法大致可以分為兩類：一類是先辨識點擴散函數，再利用傳統的復原算法進行復原；另一類是同時估計點擴散函數和原始圖像。目前成功的算法以Kundur等人提出的利用非負和有限支撐約束的遞歸逆濾波盲圖像恢復算法（NAS－RIF）［2］以及 Rudin、Chan等人提出的全變分（TV）正則化盲圖像恢復算法［3－5］最為典型。而NAS－RIF算法由于需預先知道圖像的支持域，且算法對噪聲敏感等原因，致使應用受到限制。全變分正則化盲圖像恢復算法較為成功，但由于該算法采用的是二階偏微分方程模型，在復原圖像的同時容易引起階梯效應。基于偏微分正則化方法同時估計點擴散函數和原始圖像方法中，以You和Kaveh提出的二階偏微分［6］以及Chan和 Wong提出的偏微分盲圖像復原方法［4］最為典型。但是You和Kaveh提出的算法容易引起圖像模糊，而Chan和Wong提出的算法容易引起階梯效應。P－Laplace方法［7］相對于以上方法有了很大改進，但復原出來的圖像仍然不夠理想。

為了克服階梯效應和模糊問題，很多學者做了廣泛研究［7－9］，雖然 P－Laplace方法在對圖像邊緣和內部平滑區域做分別處理時對TV復原方法中出現的階梯效應有一定的緩解作用，但仍然不夠理想。本文在不改變圖像演化方程基本性質的基礎上改進P－Laplace方法，引入參數λ調節復原過程中的保真項并對偏微分方程做單調灰度變化，進一步緩解了階梯效應，但通過大量的實驗驗證，改進的P－Laplace方法存在的階梯效應問題仍然會對圖像清晰度產生影響。在此考慮到四階偏微分方程模型較二階模型在去除噪聲和保持邊界的同時，能更好地避免階梯效應［10－12］，本文提出了一種四階P－Laplace偏微分圖像復原方法，引入了新的能量泛函，進一步避免階梯效應以提高復原圖像質量。實驗結果證明，該算法相比于TV和P－Laplace復原方法，對模糊圖像有更好的復原效果，同時也適用于水下圖像和霧天圖像的圖像復原。

1 P－Laplace圖像盲復原模型

其中：α1，α2是正的參數；p（u）為擴散控制因子，取值范圍為其值由等照度線的曲率k和梯度模值共同決定：

2 四階P－Laplace圖像盲復原

在以上P－Laplace圖像盲復原模型的基礎上，對于（6）式中的ut，將右邊乘以梯度模值u ，便得

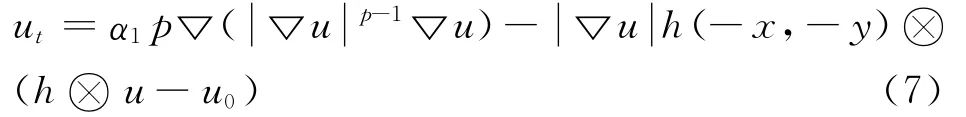
由于單調灰度變換不改變圖像演化的方程的基本性質［8］，因而改進的模型（7）是近似滿足形態學原則的，但這種改進會使階梯效應得到有效的緩解。

不少學者在克服由TV正則化所產生的階梯現象時，提出了一種有效的采用高階范數來度量圖像的方法［10－12］。考慮到四階偏微分方程模型在去除噪聲和保持邊界的同時能避免階梯效應，將四階偏微分方程引入，本文提出一種四階P－Laplace圖像盲復原方法，能量泛函表示如下：

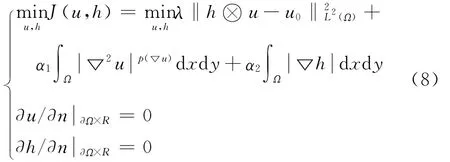
其Euler－Lagrange方程為：

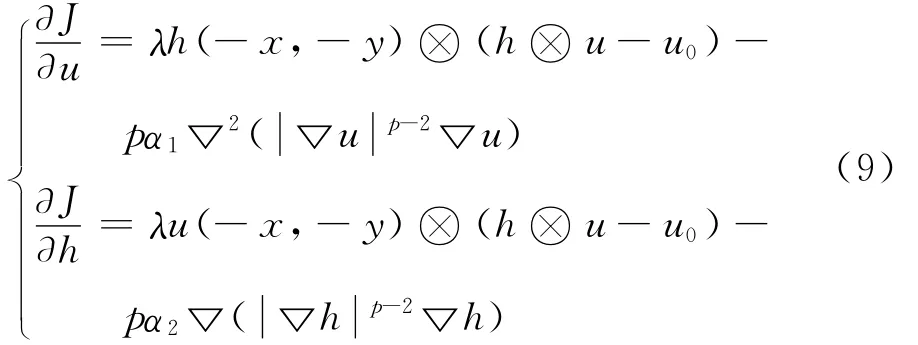
通過梯度下降流法，將模型的求解轉化為非線性反應擴散方程組，并進行單調灰度變換得：

初始值u（x，0）＝u0（x）滿足周期性條件。

由于滿足平面方程的圖像，其強度函數的Laplace算子為零并滿足Euler－Lagrange方程，因此一個平面圖像就是一個不動點，由此平面圖像就是式（9）的全局最小解［10］。采用四階偏微分方程的最大優點是由于它用分片平面圖像來近似邊界，從而消除了二階非線性擴散所造成的階梯效應。

同時，四階P－Laplace圖像盲復原模型中引入參數λ調節復原過程中的保真項，在保證復原效果的前提下，減少復原過程中的計算量。

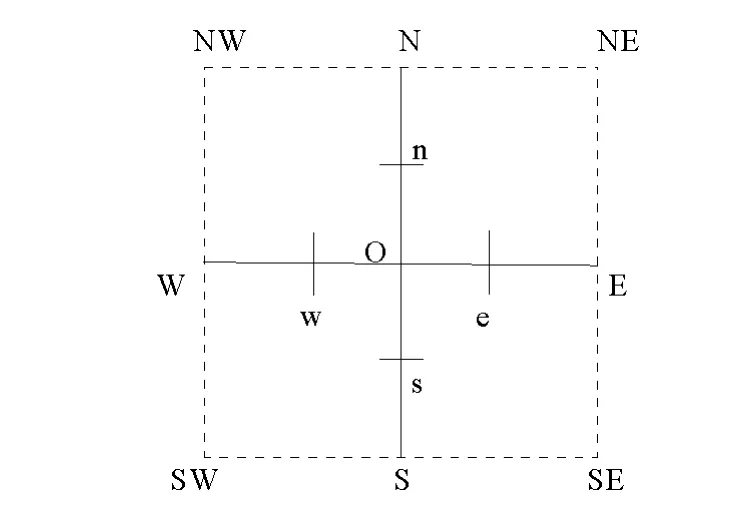
圖1 待修復像素及鄰域點示意圖Fig.1 Pixels under repaired and neighborhood point

3 數值計算方法

這里采用差分的數值計算方法，將圖像離散化，記h為空間步長，u（xi，yi，tn）記為uni，j，則ut估計用差分格式：

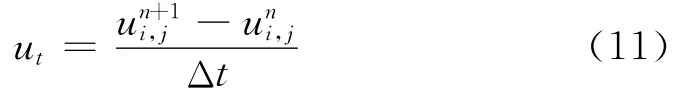
其中Δt是時間步長，用中心差分進行估計：

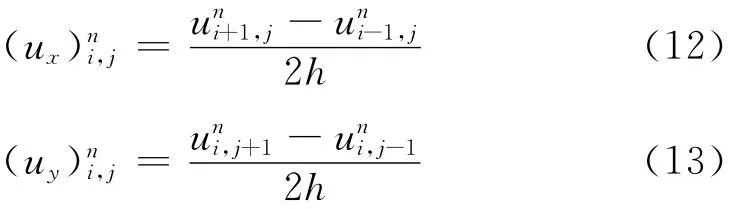
對于散度算子，這里采用半點中心差分法實現。如圖1所示，待修復點為O，N、S、W、E為O的4個鄰域點，n、s、w、e分別為對應的4個鄰域半點。令：

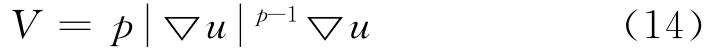
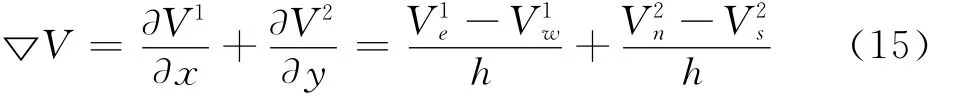
由于半點值不能直接得到，以eS點為例求解如下：

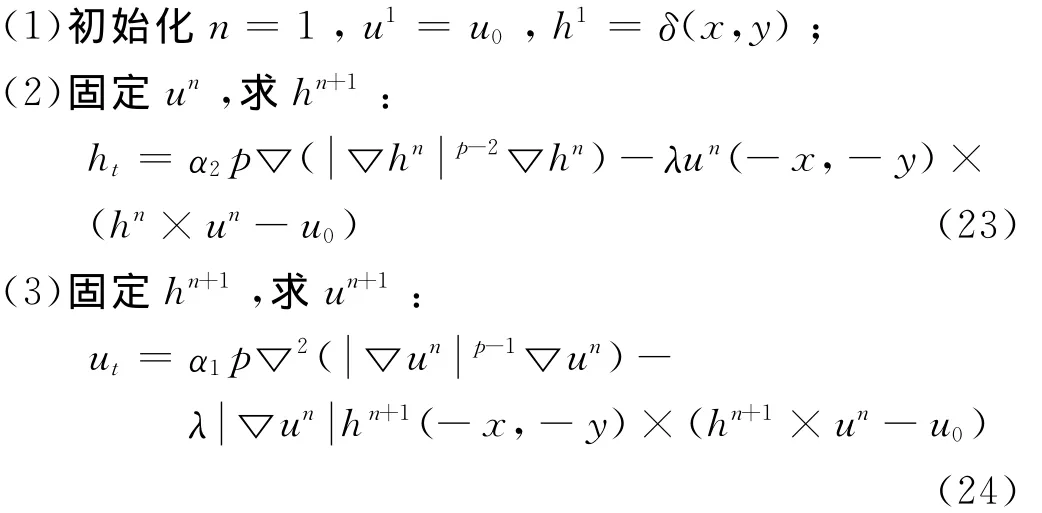
如此交替公式（23）和（24）的迭代，根據迭代次數，最終得到復原圖像。

4 實驗結果和分析

4.1 本文方法與其他方法的對比分析

為了驗證本文算法的正確性和有效性，采用大小為256×256像素的Lena標準灰度圖像作為測試圖像，分別對無噪模糊圖像和帶有不同程度噪聲的模糊退化圖像進行復原。模糊的退化圖像是利用二維高斯函數卷積核進行模糊化，噪聲是高斯白噪聲。實驗分別比較了TV復原方法、P－Laplace方法和本文方法。

實驗中，標準Lena圖像通過7×7的高斯點擴散函數進行模糊，高斯白噪聲均值為0、標準差分別取2、4、6…16，交替迭代次數為100次，參數λ＝1.5，正則化約束參數α1＝α2＝0.002。圖2為Lena清晰圖像，圖3中的4幅圖為無噪模糊圖像以及分別采用TV復原方法、P－Laplace方法和本文方法復原模糊圖像（見圖3（a））的效果圖；圖4中的4幅圖為帶噪模糊圖像（高斯白噪聲標準差為6）以及分別采用TV復原方法、P－Laplace方法和本文方法復原帶噪模糊圖像（見圖4（a））的效果圖。

圖2 Lena清晰圖像Fig.2 The sharp image Lena

圖3 無噪模糊圖像以及圖像恢復結果Fig.3 The blurred image without noise andimage restoration results

圖4 帶噪模糊圖像以及圖像恢復結果Fig.4 The blurred image with noise and image restoration results

從圖3、4可以看到，不管是無噪模糊圖像還是帶噪模糊圖像，視覺效果上TV方法的復原效果一般，PLaplace方法的復原效果有明顯改進，而本文方法的復原效果最好。用峰值信噪比PSNR值作為評價標準，表1為無噪模糊圖像以及3種復原方法復原結果的PSNR值，圖5為帶噪模糊圖像（帶有不同程度噪聲）以及3種復原方法復原結果PSNR值的走勢圖。

表1 無噪模糊圖像的復原評價Table 1 The evaluation of blurred image restoration without noise

表1顯示，對無噪模糊圖像的復原中，本文方法的PSNR值最大，有明顯的復原效果并且優于TV方法和P－Laplace方法。從圖5可以看出，當噪聲程度較低時，本文方法的PSNR值遠遠大于帶噪模糊圖像以及其他方法的復原結果，說明本文方法的復原效果是最好的。

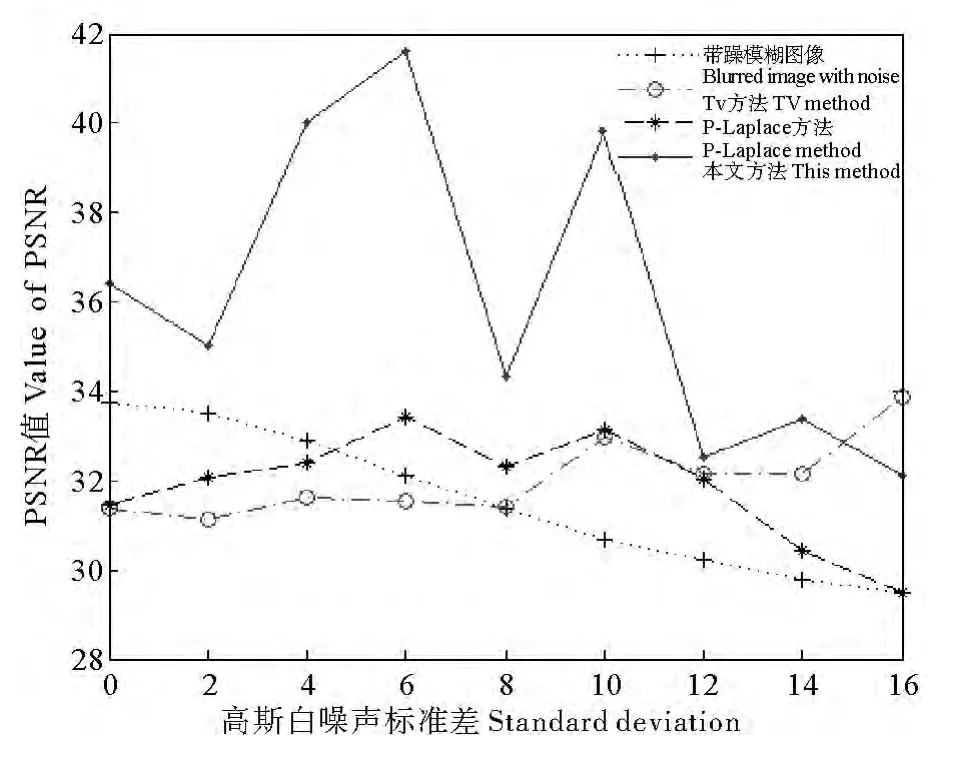
圖5 不同程度帶噪模糊圖像的復原評價Fig.5 The evaluation of blurred image restoration with noise in different level

4.2 本文方法與P－Laplace方法的對比分析

為了進一步驗證本文方法相比較傳統P－Laplace方法的優越性，實驗又采用大小為256×256像素的Lady圖像作為測試圖像，分別對無噪模糊圖像和帶有不同程度噪聲的模糊退化圖像進行復原。模糊的退化圖像是利用二維高斯函數卷積核進行模糊化，噪聲是高斯白噪聲。實驗詳細比較了P－Laplace方法和本文方法。

實驗中，Lady圖像通過7×7的高斯點擴散函數進行模糊，高斯白噪聲均值為0、標準差分別取2、4、6、8，交替迭代次數為150次，參數λ＝1.5，正則化約束參數α1＝α2＝0.002。圖6為Lady清晰圖像，圖7中的兩幅圖分別為無噪模糊圖像和帶噪模糊圖像（高斯白噪聲標準差為2），圖8中的兩幅圖為分別采用P－Laplace方法和本文方法復原無噪模糊圖像（見圖7（a））的效果圖；圖9中的兩幅圖為分別采用P－Laplace方法和本文方法復原帶噪模糊圖像（見圖7（b））的效果圖。

圖6 Lady清晰圖像Fig.6 The sharp image Lady

圖7 無噪模糊圖像以及帶噪模糊圖像Fig.7 The blurred image without noise and the blurred image with noise

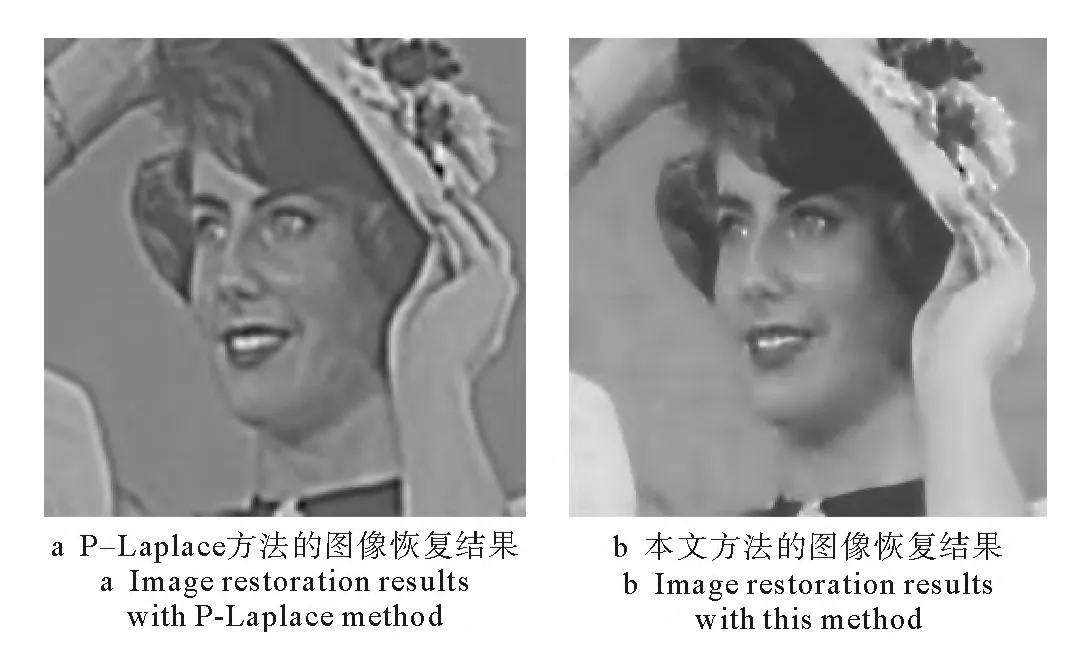
圖8 對無噪模糊圖像的圖像恢復結果Fig.8 Image restoration results on the blurred image without noise

圖9 對帶噪模糊圖像的圖像恢復結果Fig.9 Image restoration results on the blurred image with noise

從圖像恢復結果可以看出，在主觀視覺上，不管是對無噪模糊圖像的復原還是對帶噪模糊圖像的復原，P－Laplace方法的復原結果中都能看到明顯的階梯效應問題，而本文方法在去除噪聲和保持邊界的同時能避免階梯效應，相比較P－Laplace方法，本文方法有很好的復原效果。用峰值信噪比PSNR值作為評價標準，對無噪模糊圖像復原時，P－Laplace方法的PSNR值為26.75，而本文方法的PSNR值為30.36，復原效果明顯優于P－Laplace方法，表2統計了帶噪模糊圖像（帶有不同程度噪聲）以及兩種方法復原結果的PSNR值，可以看出，在相同程度噪聲干擾下，本文方法比PLaplace方法的PSNR值大，相比較P－Laplace方法有明顯的復原效果。

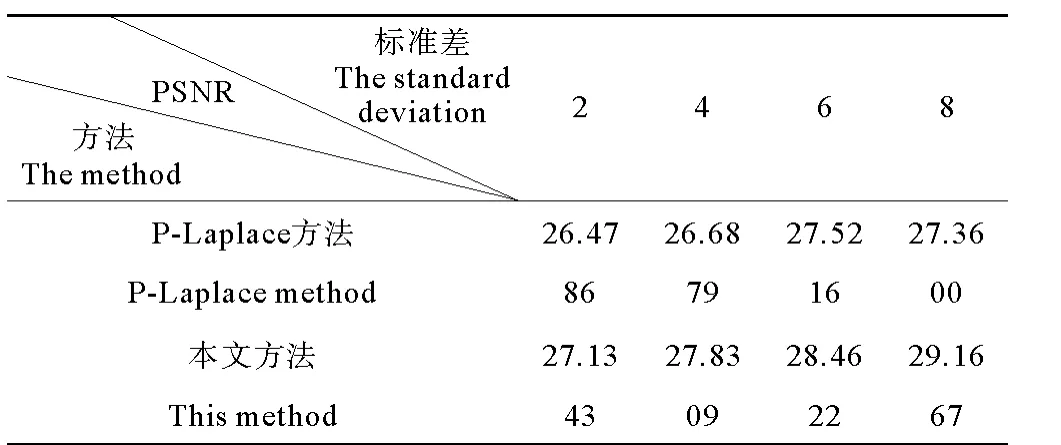
表2 帶噪模糊圖像的復原評價Table2 The evaluation of blurred image restoration with noise

4.3 本文方法的普適性研究

為了驗證本文算法的普遍性和有效性，實驗中又分別采用大小為512×512像素的Lena標準灰度圖像、水下圖像（見圖10）和霧天圖像（見圖11）做測試，復原效果如下圖顯示。

圖10 水下圖像的圖像恢復結果Fig.10 Image restoration results of the underwater picture

圖11 霧天圖像的圖像恢復結果Fig.11 Image restoration results of the fog image

從水下圖像和霧天圖像的恢復結果看，經過本文方法的圖像恢復處理，可以清楚地看到原來模糊圖像中看不清的細節，整幅圖像的清晰度也有了很大的提高，在主觀視覺上本文方法有很好的復原效果，說明本文方法也適用于水下圖像和霧天圖像的圖像復原。

5 結語

本文提出的四階P－Laplace圖像盲復原方法能夠很好地避免階梯效應，對退化圖像的圖像恢復有很好的復原效果，特別是對加性噪聲比較小的模糊圖像的圖像復原。同時，本文方法還適用于水下圖像和霧天圖像。本文方法雖然在保持邊界和細節復原方面相比其他方法有很好的效果，但從帶有不同程度噪聲的模糊圖像的圖像恢復結果看（見圖5），在噪聲程度比較大時，本文方法的復原效果一般，因此對于噪聲程度較大的退化圖像，本文方法還有待進一步改進。

［1］ Kurdur D，Hatzinakos D.Blind image deconvolution ［J］.IEEE Signal Processing Magazine，1996，13（13）：43－64.

［2］ Kurdur D，Hatzinakos D.Blind image restoration via recursive filtering using deterministic constraints ［C］.／／Proceedings of the 1996IEEE International Conference on Acoustics.Atlanta ：Speech and Signal Processing，1996：2283－2286.

［3］ Rudin L I，0sher S，Fatima E.Nonlinear total variation based noise removal algorithms［J］.Physica D，1992，60（1）：259－268.

［4］ Chan T，Wong C.Total variation blind deconvolution ［J］.IEEE Transactions on Image Processing，1998，7（3）：370－395.

［5］ Chan T，Wong C.Convergence of the alternating minimization algorithm for blind deconvolution［J］.Linear Algebra and Its Application，2000，316（3）：259－285.

［6］ You Y，Kaveh M.Blind image restoration by anisotropic regularization ［J］.IEEE Transactions on Image Processing，1999，8（3）：396－407.

［7］ 陳建軍.基于偏微分方程的圖像降噪和圖像恢復研究 ［D］.重慶：重慶大學，2009.

［8］ 王大凱，侯榆青.圖像處理的偏微分方程方法 ［M］.1版.北京：科學出版社，2008：147－151.

［9］ 馬少賢，江成順.基于四階偏微分方程的盲圖像恢復模型 ［J］.中國圖象圖形學報，2010，15（1）：26－30.

［10］ You Y，Kaveh M.Fourth－order partial differential equations for noise removal［J］.IEEE Transactions on Image Processing，2000，9（10）：1723－1730.

［11］ Chan T，Marquina A，Mulet P.High－order total variation based image restoration ［J］.SIAM Journal on Scientific Computing，2000，22（2）：503－516.

［12］ You Y，Kaveh M .Image enhancement using fourth order partial differential equations ［C］.／／Proceedings of the Thirty－Second Asilomar Conference on Signals.Pacific Grove：Systems ＆ Computers，1998：1677－1681.