利用Excel多元線性回歸分析進行測區垂線偏差分量計算

何 麗 王曉智

（中鐵大橋局集團 第一工程有限公司，河南 鄭州 450053）

1 引言

回歸分析在三角高程測量中的應用較少，主要是因為模型樣本數太少,不能充分反映測區地形狀況，模型精度較低，因而不能用于高精度的三角高程測量中。但是這樣的嘗試也給了我們一些啟發，在遠距離的高精度三角高程測量過程中，往往需要考慮垂線偏差分量的影響，為了求得這項改正，一般情況下要進行重力異常的測定或天文大地測量，工程施工測量單位做起來就有一定困難。由于垂線偏差的求解方法較為復雜，采用常規模型的話，模型參數往往不易求得，且精度也無法保證。因此，作者嘗試從數理統計的原理出發，根據有限的測區高精度GPS基線控制網資料，對測區內的垂線偏差分量的求解方法進行一些探索。

2 回歸分析原理

回歸分析是一種處理變量的統計相關關系的一種數理統計方法。回歸分析的基本思想是：雖然自變量和因變量之間沒有嚴格的、確定性的函數關系,但可以設法找出最能代表它們之間關系的數學表達形式。

多元回歸分析是研究多個變量之間關系的回歸分析方法,按因變量和自變量的數量對應關系可劃分為一個因變量對多個自變量的回歸分析(簡稱為“一對多”回歸分析)及多個因變量對多個自變量的回歸分析(簡稱為“多對多”回歸分析),按回歸模型類型可劃分為線性回歸分析和非線性回歸分析。在本文中，為簡單起見，僅采用多元線性回歸分析的方法，對垂線偏差的求解方法進行一些初探。

3 垂線偏差的概念

同一測站點上鉛垂線與橢球面法線之間的夾角u，即是垂線偏差。u通常用南北方向分量ζ和東西方向分量η表示。參見圖1。

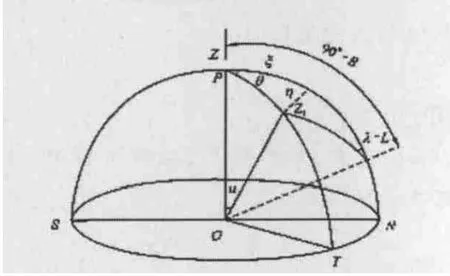
圖1

地面點的垂線同其在橢球面上對應點的法線之間的夾角u（見圖1），它表示大地水準面的傾斜。垂線偏差通常用兩個分量來表示，一個是子午圈分量ξ，即垂線偏差南北分量；一個是卯酉圈分量η，即垂線偏差東、西分量。

3.1 垂線偏差公式

根據肖榮健教授等人研究，我們可以較為方便地利用兩條GPS基線邊求得測區特定區域的垂線偏差分量。其公式為：

從上式可知，ξ、η的精度受基線之間的夾角影響明顯，因此使用GPS測定垂線偏差時應特別關注兩基線之間的夾角不宜太小。

由于用GPS獲得基線間的距離、大地高非常容易，基線間的正常高差也可很快求得，在面積不大且地形呈線性變化的地區，用GPS測定垂線偏差是種理想的途徑，其結果精度已有研究者證明與精密天文大地方法相當[1]。

3.2 試驗區域垂線偏差情況

三角高程測量有顯著的優點，但在丘陵和山區，由于地形起伏較大，根據目前的研究成果，垂線偏差的變化也較大，這就使得測點之間所觀測的高差不等于這兩點之間的正常高高差，因此，進行遠距離單向三角高程測量時必須進行垂線偏差改正。

我們試驗依托在建的南澳大橋項目位于廣東省東北部，為連接汕頭市南澳縣與汕頭市區的一座跨海大橋，根據我們計算得出的試驗區域垂線偏差的情況來看，類似于平原地區，最大值為4″，最小值為 2″，在 2km左右范圍內，變化范圍為 0.015″～0.36″，平均變化率約0.17″。根據嚴密三角高程測量計算公式[2]：

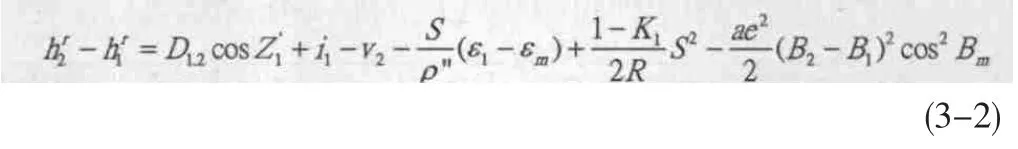
為簡單方便，我們這里使用測區計算出的垂線偏差分量均值代替。即使在平原地區，對于2km的距離，其對高差的影響最大約為3.5mm，因此在進行遠距離單向三角高程觀測的時候，即便是垂線偏差變化不大的地區也不能不考慮其對高差的影響。因此，在地形復雜地區觀測測量時，應該適當減小視線的長度，進行遠距離單向觀測時，必須加入垂線偏差改正。

4 利用Excel進行多元線性回歸分析輔助進行測區垂線偏差分量計算

一元線性回歸分析用模型中的一個自變量X來估計因變量Y。但由于客觀事物的聯系錯綜復雜,一個因變量的變化往往受到兩個或多個自變量的影響。為了全面揭示這種復雜的依存關系,準確地測定它們的數量變動,提高預測和控制的精確度,就要考慮更多的自變量,建立多元回歸模型。多元回歸的計算難度要遠大于簡單線性回歸,且變量越多,計算越復雜，但應用Excel來完成計算將變得簡單和輕松。

我們就用以下圖中的數據為例簡單探討一下利用Excel進行多元線性回歸分析輔助進行測區垂線偏差分量的計算方法。

表4-1 基線端高差和距離與垂線偏差分量ξ的原始數據

多元線性回歸的Excel數據分析操作方法首先單擊工具欄,在彈出的菜單中選擇加載宏，在彈出的宏加載項中選擇加載分析工具庫，確定后再在工具欄中選擇數據分析,在數據分析工具的選項框中選中回歸,然后在輸入、輸出選項以及有關的選項框中進行適當的選擇,必須注意在進行自變量X的輸入時要按照已經確定的各個自變量的順序把所有自變量的單元格引用范圍一起放在X值的輸入區域內。具體流程見圖2。

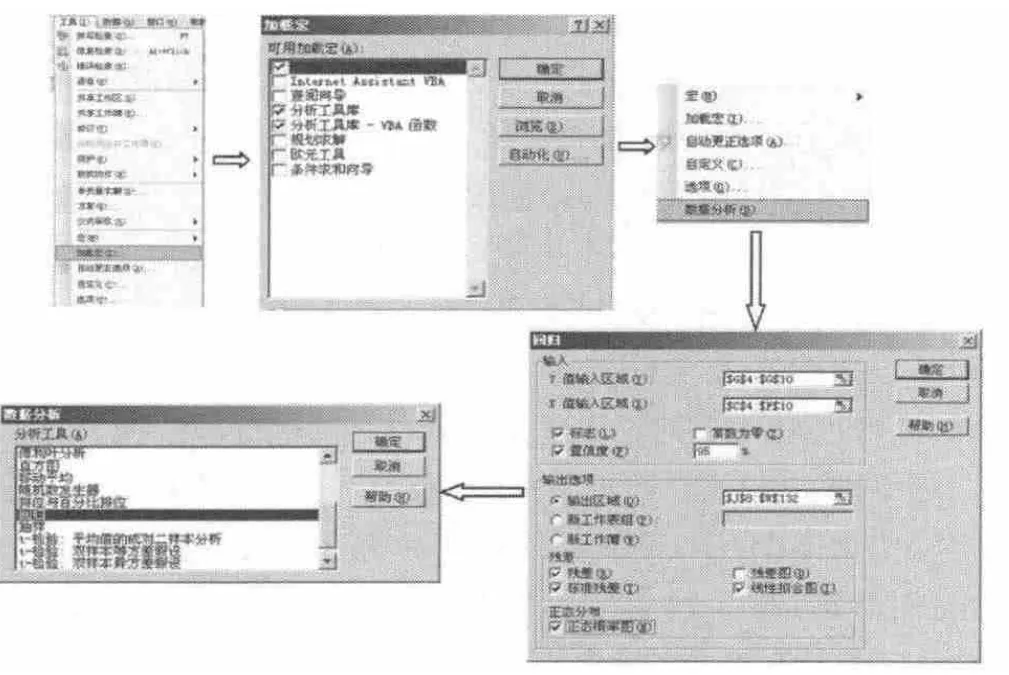
圖2 多元線性回歸分析流程圖

點擊“確定”按鈕,即可得到線性回歸分析的結果。見圖3。

圖3 垂線偏差線性回歸分析計算結果

根據上圖中的顯示結果,可直接寫出線性回歸方程：

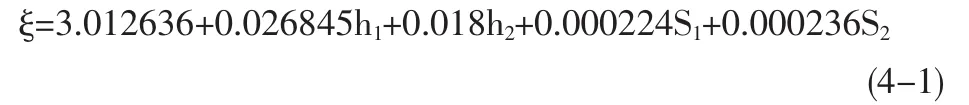
計算結果中，列Significance F對應的是在顯著性水平下的Fα臨界值，其實等于P值，即棄真概率。所謂“棄真概率”即模型為假的概率，顯然1-P便是模型為真的概率。可見，P值越小越好。對于本例，P=0.00888＜0.01，故置信度達到99%以上。

利用該式，就可以方便地求得測區范圍內任何地方進行的三角高程測量的垂線偏差分量的改正值，而無須再進行長時間的GPS靜態觀測以求得測線兩端的垂線偏差分量。

5 測區垂線偏差分量改正應用

根據上一節中的計算分析，我們進行了單向觀測的試驗，試驗選擇的直線距離為720m，兩點之間的高差按照二等水準的測量精度精確求得。根據計算得出的測區平均垂線偏差值為3.3963″，結合回歸分析的計算模型計算得試驗距離上垂線偏差值為3.3603″，可以計算出試驗距離垂線偏差的影響約為：

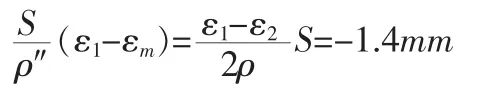
這個數值對于精密三角高程測量來說，是不能不考慮的。試驗的結果經大氣折光和垂線偏差以及橢球改正后，精度大為提高，也說明此法的可行性，具有一定的實用價值。

6 結論

如果樣本數量更多，置信度也許會更高一些，或者采用非線性回歸分析，會更符合現場的實際情況，限于時間和篇幅，本文暫不做更深入的研究，僅限于提供一種思路和方法。

Excel是Office家族的一個成員，是功能強大、使用方便的電子表格式數據綜合管理與分析系統，可用來記錄和整理試驗數據。另外，Excel也具備一些統計運算的功能，若能巧妙地使用，也可以解決一些較為復雜的測量統計運算問題，如多元非線性回歸的問題等。

從本例中可以看出，其實基線距離S1和S2對于測區垂線偏差的影響不顯著，影響較大的是基線兩端的高差。因此，在平原地區，距離較短、精度要求較低時可以不考慮垂線偏差的影響，但是遠距離或在地形起伏較大的山區進行高精度的三角高程測量，就必須要考慮垂線偏差的影響了。

[1]肖榮健，鄒強.垂線偏差的確定方法[J].大眾科技，2009（8）.

[2]肖根旺，許提多，周文健，朱順生.高精度三角高程測量的嚴密公式[J].測繪通報，2004(10).

[3]李建忠.用GPS測定垂線偏差[J].測繪工程,Vol.8,No.2,1999.

[4]王愛國.大氣折光和垂線偏差影響的三角高程測量的精度分析[J].西部探礦工程2007，3.

[5]龔江，石培春，李春燕.巧用Excel解決多元非線性回歸分析[J].農業網絡信息，2011（01）.