基于BP神經網絡的黃金價格預測分析

凌 晨，張驊月

(南開大學經濟學院 天津 300071)

0 引 言

當今國際金融體系中，在黃金非貨幣化后，各國逐步放松了對黃金的管制，于是全球黃金市場得到極大發展，并已成為與股票市場、期貨市場、債券市場、外匯市場等并列的金融投資市場。據倫敦國際金融服務機構(IFSL)統計，2008年交易所黃金期貨的成交金額增長了約 83%，達到記錄高點 5.1萬億美元。2008年僅COMEX、TOCOM和MCX三家交易所的黃金總交易量就達 48.28億盎司，同比增長 47%，交易額達4.32萬億美元，同比大幅增長89%。在此背景下，黃金價格也成為一個有意義的分析研究與預測的對象。

國際黃金市場有著極高的換手率與交易總額，波動劇烈，是一個非常復雜的非線性動態系統，同時，沒有任何一個多方或者空方可以有如此大的實力去左右國際黃金市場價格。因此，較之有內幕交易的股票市場等而言，國際黃金市場是一個極完備的競爭市場。在這個非線性動態系統中，線性預測方法等主流分析方法面臨著挑戰，很難揭示市場內在的規律，因而眾多的預測分析方法的應用效果都難如人意。

近年來，計算機技術和人工智能為非線性混沌系統的建模和預測提供了許多新的技術與方法，其中人工神經網絡(Artificial Neural Network)是近年來發展起來的一個分支，有著活躍的生命力。實踐證明，ANN除了可在語言識別、自動控制領域應用，還可在預測、評價等方面發揮作用，并且有研究表明，其準確性明顯優于自回歸模型。BP神經網絡(Back-Propagation Neural Network)就是其中的一種。本文使用 BP神經網絡對黃金的價格進行預測與分析，得出了精度較高的預測結果。然而BP網絡也存在某些不足，筆者在文章最后也提出了運用 BP網絡進行預測的某些局限性以及相關的建議與意見。

1 BP神經網絡工作原理

本文利用 BP網絡預測 LIFFE倫敦國際金融期貨交易所的倫敦金價格，是根據 BP網絡的映射原理，基于主成分分析，假設黃金價格與美元指數、原油價格之間存在映射關系 F，設計的 BP網絡就是在輸入和輸出過程中建立起非線性映射關系以實現 F值的最優逼近。

BP神經網絡，就是加入了誤差反傳、誤差反向傳播算法的人工神經網絡學習過程，是對非線性可微分函數進行權值新聯的多層前向網絡，由信息的正向傳播和誤差的反向傳播兩個過程組成。輸入層用于接收來自外界的輸入信息，并傳遞給中間層各神經元；中間層是處理層，用于處理信息變換，根據不同精度的需求，中間層可以設計為單隱層或者多隱層結構；最后一個隱層將處理后的信息傳遞到輸出層，經進一步處理后，完成一次學習的正向傳播處理過程，由輸出層向外界輸出信息的處理結果。如果實際輸出值與期望輸出值不相符時，誤差會進行反向傳播，即誤差通過輸出層，按誤差梯度下降的方式修正各層權值，向隱層、輸入層逐層反傳。周而復始的信息正向傳播和誤差反向傳播過程，使各層權值不斷調整，從而達到對神經網絡新聯的目的，此過程會一直持續到網絡輸出的誤差減少到之前設定的門檻值以下，或者達到預先設定的學習次數后才會停止。其拓撲結構如圖1所示。

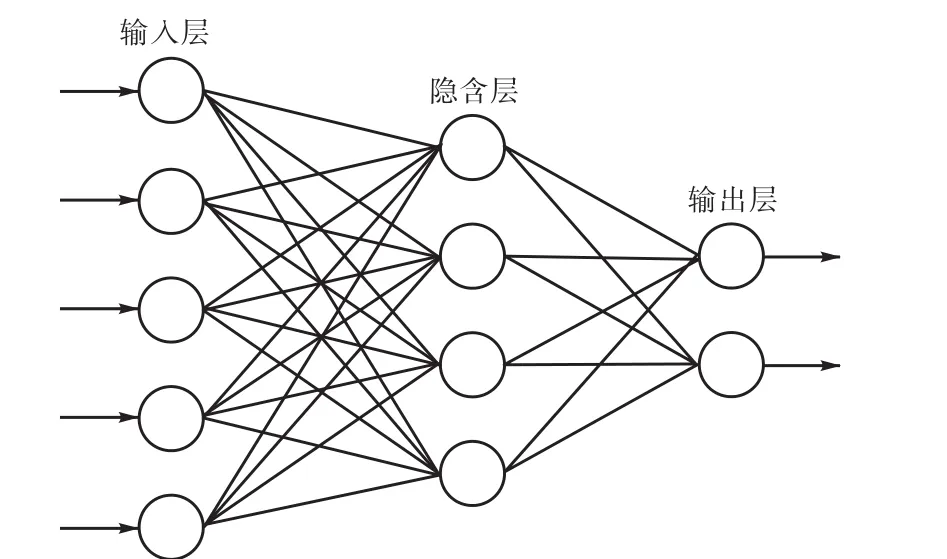
圖1 BP神經網絡拓撲結構Fig.1 BP neural network topology

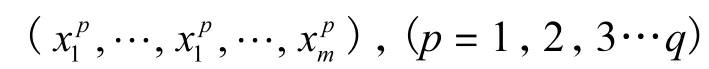
矢量 X進入輸入層后，各隱含層、輸出層神經元激活值為：

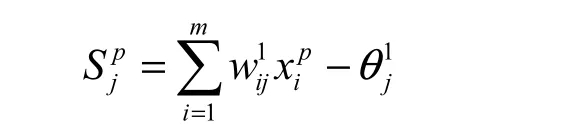
(j＝1，2，…l；j＝1，2，…m；p＝1，2，…q)(w 為權值，θ為閾值)

激活函數一般采用sigmoid()函數，即：

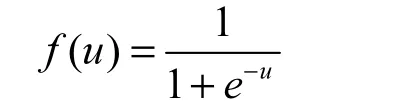
帶入并整理后得到第k節點的輸出值分別為：

反向計算時，輸出層的校正誤差及其應校正的權值和閾值分別為：

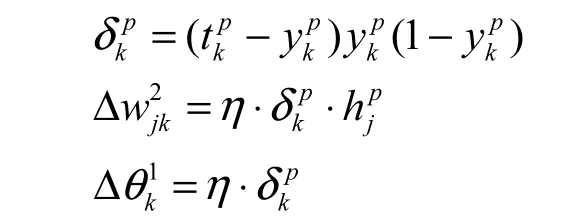
2 數據分析與預測

2.1 數據的選取

本文選擇 IMM 國際貨幣市場 2013年 4月 1日—2013年7月26的美元指數期貨，以及NYMEX紐約商品交易所2013年4月1日—2013年7月26日的 NYMEX原油價格作為其他解釋變量，選取LIFFE倫敦國際金融期貨交易所2013年4月5日—2013年8月1日106個交易日的倫敦金價格作為輸出變量(使用實時價格輸入變量估計輸出變量是沒有可操作性的，因此我們取輸出變量的四階滯后，更加具有實用性與可操作性)。選取 LIFFE倫敦國際金融期貨交易所2013年8月5日—2013年9月1日的倫敦金價格作為對比數據；IMM 國際貨幣市場 2013年8月1日—2013年8月26日的美元指數期貨，以及 NYMEX紐約商品交易所 2013年 8月 1日—2013年8月26日的NYMEX原油價格作為測試時輸入變量。

2.2 變量預處理

2.2.1 歸一化處理

歸一化是一種無量綱處理手段，使物理系統數值的絕對值變成某種相對值關系。為消除各維數據間數量級的差別，簡化計算，避免因變量數量級差別較大而造成的模型預測誤差。本文先將變量控制在(0，1)，但發現在0.01的精度上變化不大，因此為所有變量都擴大了104倍，便于后期觀察與計算。

2.2.2 隱含層節點數確定

BP網絡隱含層節點數的數量會影響到 BP網絡預測精度，例如，如果節點數太少，神經網絡的訓練能力就會變弱，無法完成精確預測；但若節點數過多，會延長訓練時間，并且可能過度擬合。所以只有適當的節點數才能使 BP網絡的性能得到最大發揮，筆者根據前人經驗以及多次試驗與比較，最終確定了隱含層節點數分別為7和13。

2.2.3 BP網絡結構確定

本文采用Matlab 7.0的BP神經網絡工具箱來進行仿真試驗。用 newff創建 BP神經網絡，設置 2個隱含層，傳遞函數是 tansig，訓練函數為 traingda，最大訓練次數為1,000次，目標精度為0.001。

2.3 平穩性檢驗

數據變量的平穩性是傳統的計量經濟分析的基本要求之一。只有模型中的變量滿足平穩性要求時，傳統的計量經濟分析方法才有效。平穩性檢驗是為了排除偽回歸現象，即數據的高度相關僅僅是因為二者同時隨時間有向上或向下的變動趨勢，并沒有真正聯系。有偽回歸情況的數據在殘差分析中無法準確進行分析。在本文中進行了單位根、自相關和長記憶性檢驗，得出觀測樣本是非平穩、具有長記憶性的序列，不適于使用傳統計量模型進行預測，而應使用BP網絡進行預測分析。

2.3.1 單位根檢驗

由au_close的單位根檢驗結果可知，單位根統計量 ADF為-2.210,196遠大于給出的顯著性水平1%～10%的臨界值，所以接受原假設，即該序列是非平穩的。待預測序列au_close的ADF檢驗結果如下表所示：

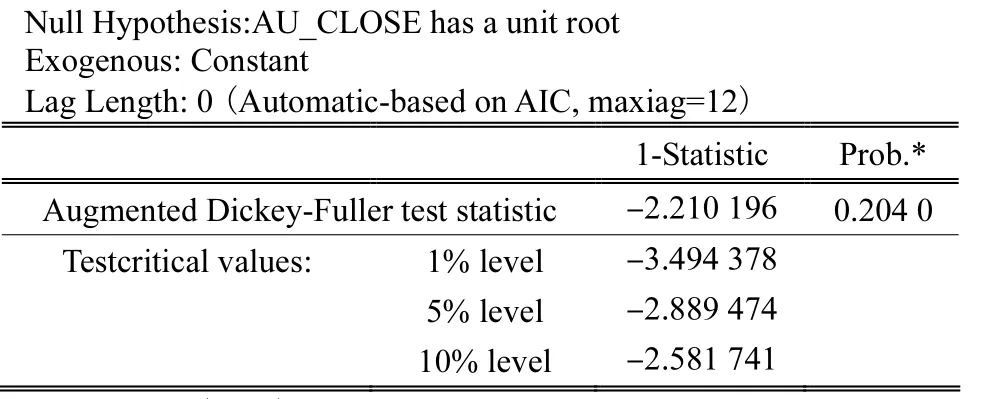
表1 au_cl ose的ADF檢驗結果Tab.1 ADF testing results for au_close

?

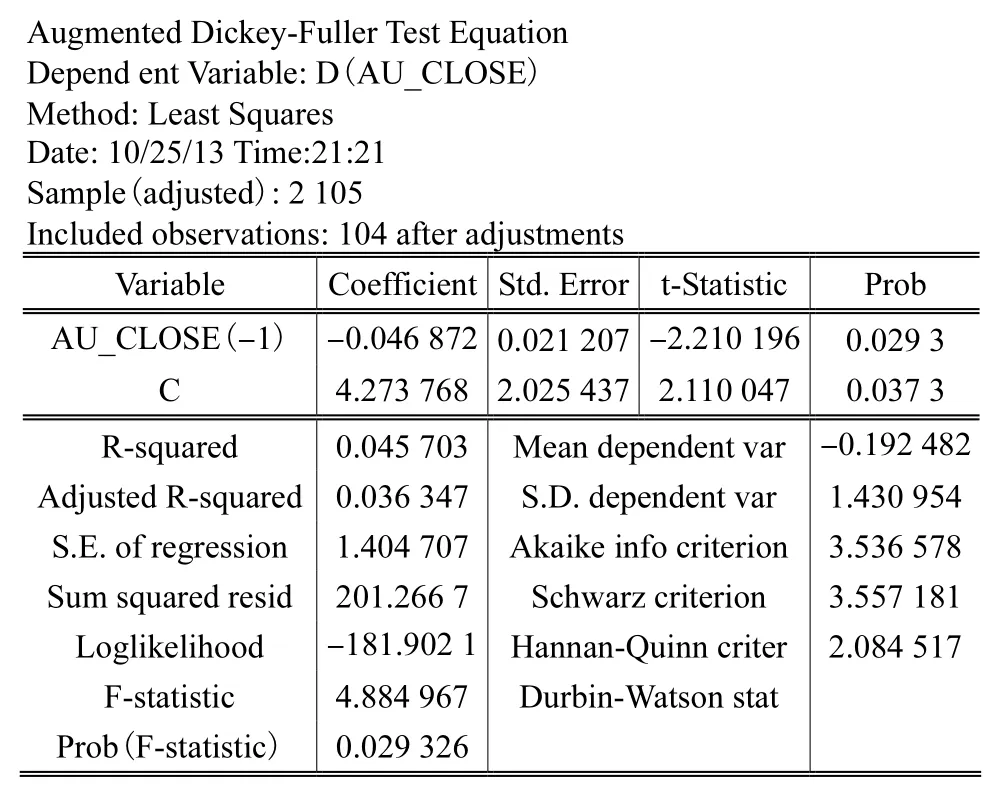
2.3.2 自相關和偏自相關檢驗(見表2)

根據該樣本的自相關和偏相關圖表我們可以看出樣本的自相關、偏相關系數在最初的d階遠遠大于兩倍標準差的范圍，而后幾乎70%的自相關系數都落在2倍標準差周圍，并且由較大的自相關系數衰減并收斂到某一值的過程非常緩慢，于是，可以認為這是一(偏)自相關系數拖尾，適合用 BP網絡進行分析。檢驗結果如表2。

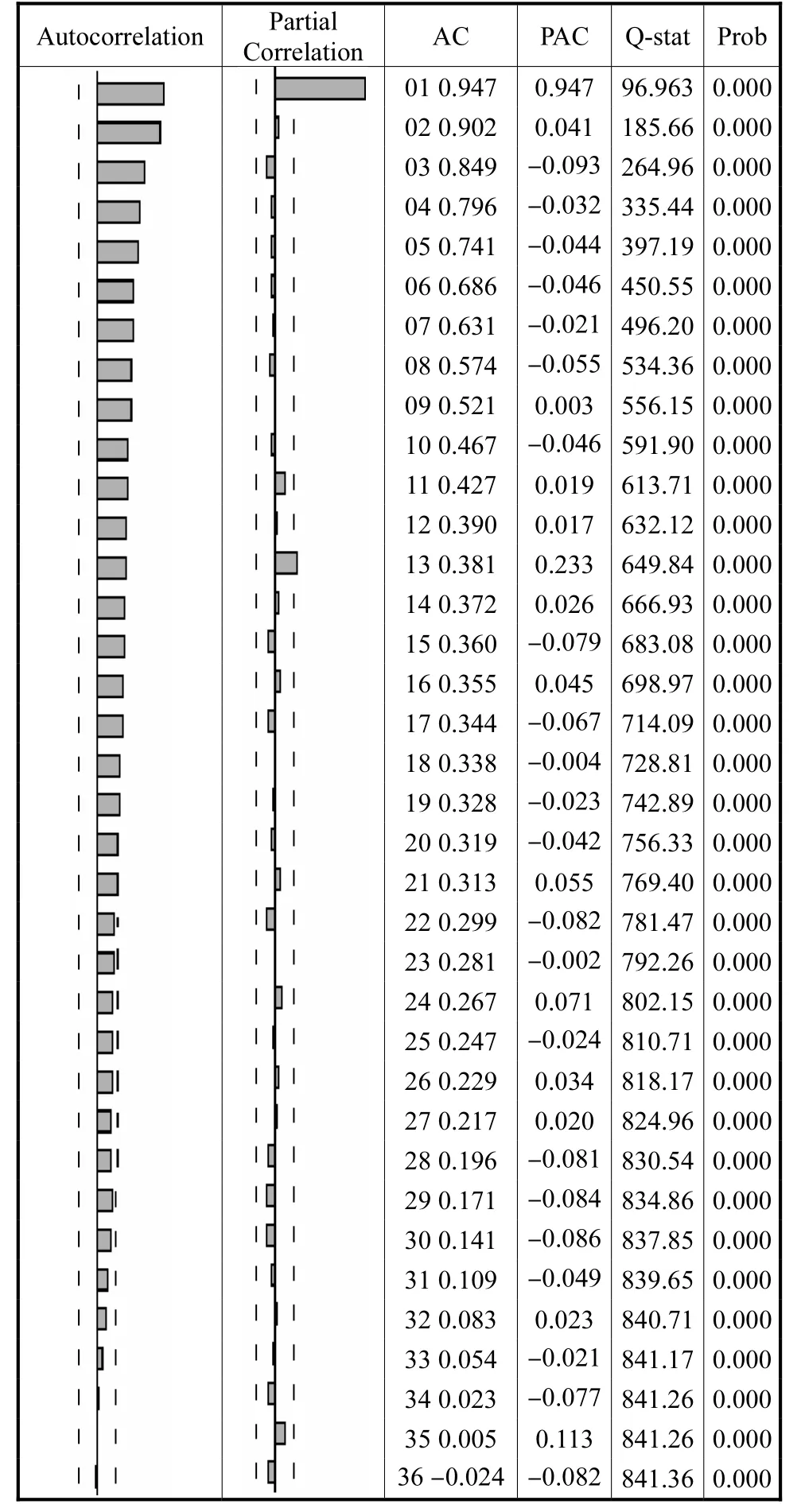
表2 au_cl ose的(偏)自相關檢驗Tab.2 Partial(auto)correlation test results for au_close

2.3.3 長記憶性檢驗

本文中運用 HURST指數進行檢驗，HURST指數檢驗方法是一種被用于資本市場的混沌分型分析的方法。當H指數等于0.5時，表示原時間序列是一個隨機序列，即過去的觀測值與將來的值不相關，這通常是概率統計學的研究范圍；當 H指數在(0.5，1.0)時，表示所研究的時間序列是一個持久性序列，即過去的觀測值與將來的值正相關，具有長程相關性；當 H在(0，0.5)時，原序列為反持久性序列，即過去的觀測值與將來的值負相關，序列有突變跳躍逆轉性。運用 matlab 7.0計算得出該序列的 H指數為0.915，這表示黃金市場有著非常明顯的長記憶性，有偏隨機游動市場，具有混沌分性特征，非常適合使用BP神經網絡進行分析預測。

2.4 神經網絡模型的構建

2.4.1 BP網絡拓撲結構的設計

網絡結構的設計包括確定網絡的隱層數、隱層結點數及輸入輸出結點數。一般來說，對于某個單個神經元，即使有多個輸入也不能滿足實際需求，需要有多個并行的神經元，這些神經元組成的集合就是“層”。輸入向量進入網絡的權矩陣 W 的列下標表示該權的輸入源神經元，行下標代表輸出的目的神經元。

圖2 單層網絡結構Fig.2 Monolayer network structure

于是具有 S個神經元，R個輸入的單層網絡結構。如上圖 2所示(b為偏置值向量)，我們可以得出a＝f(Wp＋b)。那么多層神經元的網絡就可以寫做a3＝f,3(W,3,f,2(W2,f,1(W1,p＋b1)＋b2)＋b3)。一般情況下，采用單隱層的三層網絡，確定隱層結點數的方法采用試驗湊試法。

輸入輸出層結點數由實際問題決定。對于時間序列預測的問題，輸入層結點數取決于數據的多少。可先將序列分為訓練部分和檢驗部分。再不斷調試輸入結點數，并檢驗其精確度。最后應采用當結點數增加而誤差不隨之減小的臨界值。

2.4.2 BP網絡訓練過程

人工神經網絡訓練就是指給該 BP網絡一個初始權值，用訓練樣本根據 BP算法的步驟對該網絡進行反復訓練，直到網絡收斂于某一標準值域。如未達到效果，可以調整網絡的初始權值達到期望效果，若還不理想則可更改網絡的拓撲結構，直至達到滿意的訓練結果。本樣本中，cost的變化見圖3。

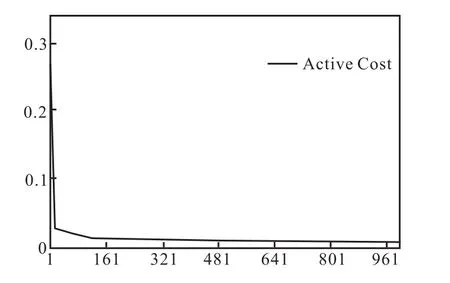
圖3 Active costFig.3 Active cost

2.4.3 結果分析本次實驗共進行了6次訓練，每次的結果指標如下表3所示

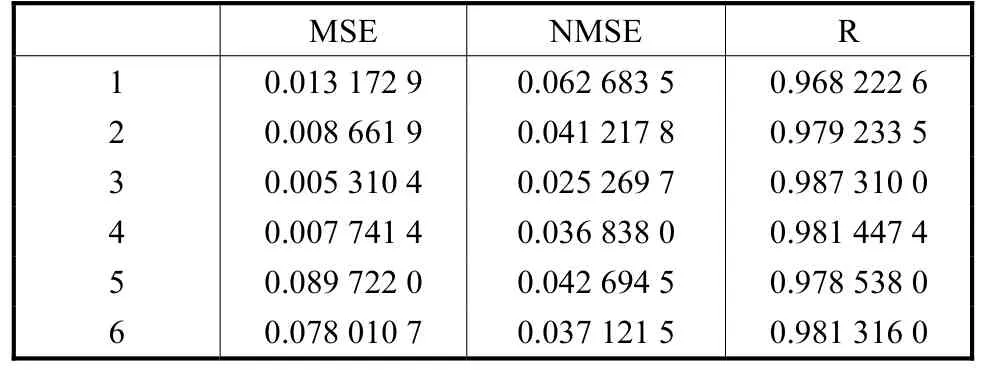
表3 訓練結果指標Tab.3 Indicators of drilling results

由于擬合優度并沒有固定的變化趨勢，所以經過比較后選取效果最優的第3次訓練結果。該次訓練擬合后均方誤差 MSE為 0.005,310,4，NMSE為0.025,269,7，擬合優度r為0.987,31，即表示該模型可以解釋 98.731%的觀測值。可見該 BP網絡在經過大量和充分的訓練后，確實在外部形式上擬合了數據，在內部數據中總結出了觀測值蘊含的變化規律，具有很高的可信度。我們選取第 3次的權重進行測試，測試結果如圖4所示，誤差項散點如圖5所示，其中粉色的折線是觀測值，藍色的折線是模型預測的結果。

從預測結果可以直觀地看出在 t0～t12的時間范圍內，該網絡具有很高的可信度，但隨著時間的推移，后續預測雖然在波動上與觀測值大體一致，但是在數值上卻有所差異，觀測值的標準差為 2.908,4，根據預測值誤差項可以看到接近 80%的預測值都在2倍標準差的范圍內，所以該模型的精度較高，并且非常適用于短期預測，但對預測長期走勢會有一定的偏差。

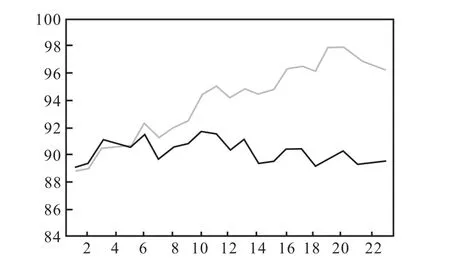
圖4 預測值與實際值折線圖Fig.4 Line chart of predicated value and actual value

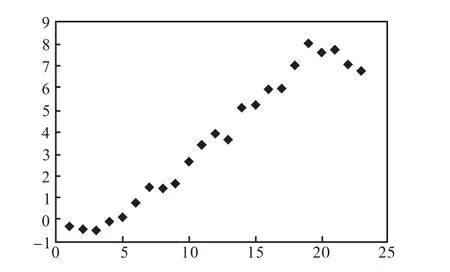
圖5 預測值誤差項Fig.5 Error terms of predicted value

3 局限與建議

人工神經網絡模型所包含的放生觀點為我們帶來了與傳統方法截然不同而又非常具有開發價值的研究方向，其中的有關的思想和技術的應用，很大程度上推進了非線性系統價格預測的問題。而BP神經網絡模型，作為 ANN的一個重要組成部分，毋庸置疑，將會在今后的經濟學金融學領域中得到更為廣泛的應用。然而，事情的發展都是兩面的，筆者總結出在實際操作中本 BP神經系統的一些局限性及其改善建議：

① 該BP神經網絡的滾動優化算法的收斂速度較慢。由于神經網絡優化控制是多步預測的，通常計算量較大，求解復雜，而且隨著預測步數的增多需要考慮到的情況迅速增加，更為復雜，難度將呈指數遞增。雖然已經有大量文獻對此作了研究與探索，但始終無法完全解決設計復雜、計算量過大的問題。

② 每次計算結果都有較為明顯的區別，無法確定最佳結果出現的時間。這是由于網絡每次隨機初始化，相當于是隨機產生誤差曲面，而 BP算法有沒有很強的全局尋優能力，容易陷入局部極小點，因此每次收斂位置不同，不易找到全局最優解。

③ 該 BP神經網絡多目標優化能力不強，難以擺脫決策過程中的隨機性和模糊性。我們知道，智能控制不僅在處理復雜系統時能進行有效的控制，同時在學習、組織、自適應和優化方面都表現出很強的優勢。為了解決復雜的黃金市場價格波動中的不確定性以及多目標優化問題，我們可將智能控制中的其他一些方法，比如模糊控制、遺傳算法或專家系統等，積極地引入到神經網絡預測中進行共同研究，幫助完善人工神經網絡的預測結果。

④ 僅有少量的輸入指標參與該網絡的構建。由于基于主成分分析，本文僅選取了幾個有代表性的指標，如果將大量的指標都作為神經網絡的輸入變量，會增加網絡的復雜度并降低其學習的收斂速度、泛化能力以及會出現過度擬合的現象。多成分的分析會導致該網絡計算時間大大延長，甚至會影響計算的精度。因此，在有效保留信息的前提下對數據進行降維也應是未來人工神經網絡的研究方向之一。

⑤ 運用BP網絡算法構建的預測模型對觀測值的預測表現出一定的成功率。同時也可發現這種預測方法得出的結果僅可以表現出觀測值在將來的波動狀況狀態，而不是絕對處于某種狀態，也并不能得到預測值的具體數值。由于黃金市場價格的波動是一個復雜的非線性混沌系統，其價格的變化受到多方面的影響，其中不僅包括美元指數、原油價格，還包括基本面、政策、宏觀經濟走勢以及人們的心理預期等等。因此，在擬合模型的過程中應廣泛收集不同層面的信息進行并列分析與判斷，以提高預測結果的完備性與有效性。

4 結 語

由于黃金市場價格的非平穩性，傳統計量統計學不能做到精確預測，于是本文建立了一種基于 BP神經網絡的黃金價格預測模型，運用主成分分析，預測結果表明該模型有很大的可信度。同時，筆者還給出了 BP神經網絡在作為黃金價格的預測模型時的一些優化建議。由于國際黃金市場同時受心理預期、政治政策、經濟走勢等人為因素的影響較大，內在規律非常復雜，神經網絡技術雖然可以在一定程度上幫助人們進行一些非線性混沌系統行為的預測，但是為了使預測模型達到更加精準的程度尚需進一步研究與挖掘。■

［1］ 常麗娟，劉德運，許燕紅. 白銀市場與黃金市場收益率波動溢出效應研究[J]. 科學經濟社會，2011(4)：18-24.

［2］ 房毅憲，王寶文，王永茂. 基于遺傳算法的動態遞歸網絡的股價預測[J]. 燕山大學學報，2007(4)：359-363.

［3］ 郭彥峰，肖倬. 中美黃金市場的價格發現和動態條件相關性研究[J]. 國際金融研究，2009(11)：75-83.

［4］ 劉柯. 基于主成分分析的 BP神經網絡在城市建成區面積預測中的應用——以北京市為例[J]. 地理科學進展，2007(6)：129-137.

［5］ 李萍，曾令可，稅安澤，等. 基于MATLAB的BP神經網絡預測系統的設計[J]. 計算機應用與軟件，2008(4)：149-150，184.

［6］ 劉星，張漢榮，萬迪. 股價預測的基本分析方法[J].中外企業家，1995(2)：36-37.

［7］ 李松，羅勇，張銘銳. 遺傳算法優化 BP神經網絡的混沌時間序列預測[J]. 計算機工程與應用，2011(29)：52-55.

［8］ 湯凌冰，廖福元，羅鍵. 模糊神經網絡在股價預測中的應用[J]. 系統工程，2004(2)：107-109.

［9］ 唐萬梅. BP神經網絡網絡結構優化問題的研究[J]. 系統工程理論與實踐，2005(10)：95-100.

［10］ 汪淼，羅劍. 運用馬爾科夫預測法構建股價預測模型[J]. 經濟師，2005(1)：34-35.

［11］ 溫博慧. 國內外黃金價格波動性及其演化的實證研究——以中國上海和英國倫敦黃金市場為例[J]. 世界經濟情況，2008(10)：59-64.

［12］ 吳立揚，周波. 基于人工神經網絡的股價指數預測[J]. 知識經濟，2009(1)：62-63.

［13］ 楊成，程曉玲，殷旅江. 基于人工神經網絡方法的上市公司股價預測[J]. 統計與決策，2005(24)：106-108.

［14］ 許興軍，顏鋼鋒. 基于 BP神經網絡的股價趨勢分析[J]. 浙江金融，2011(11)：57-59，64.

［15］ 翟敏，華仁海. 國內外黃金市場的關聯研究[J]. 產業經濟研究，2006(2)：30-35.

［16］ 張暉，許文新. 國際黃金市場發展狀況及其趨勢分析[J]. 上海金融學院學報，2007(6)：15-21.

［17］ 張文鴿，吳澤寧，逯洪波. BP神經網絡的改進及其應用[J]. 河南科學，2003(2)：202-206

［18］ 趙夢辰，黃棟超，馮宇皓，等. 人工神經網絡在股價預測中的應用[J]. 時代金融，2012(15)：242.

［19］ 趙姚陽，濮勵杰，胡曉添. BP神經網絡在城市建成區面積預測中的應用——以江蘇省為例[J]. 長江流域資源與環境，2006(1)：14-18.