基于偏正態分布的SN-ARCH(q)模型及應用
徐 燕,陳平雁
(南方醫科大學 公共衛生與熱帶醫學學院生物統計學系,廣州 510515)
時間序列分析在生物、醫學、氣象、天文、地質、經濟等領域廣泛應用,尤其是在經濟金融領域,如匯率、股票價格、收益率等。由于各時刻的條件均值和方差難以滿足常數的假設,Engle(1982)提出自回歸條件異方差模型,條件均值和方差分別依賴于t時刻之前的觀察值和誤差平方,并表示為過去值的函數,這意味著其條件方差非常數,從而滿足了要求。
Hagan和Leonhard(1976)在正態分布中引入刻畫偏度的形態參數而得到新的分布稱為Skew Normal Distribution,簡稱SN分布,處理偏態數據效果良好[1]。
本文首先介紹SN分布概念,然后給出SN-ARCH(q)模型及參數中位數無偏估計,最后報道實驗結果。
1 SN分布
近年來基于某些對稱分布的偏斜分布族被大量研究,如正態分布、t分布、Cauchy分布等[1,2,3]。這類問題的關鍵在于引入偏斜參數后得到參數方程的分布形式及參數估計。
1.1 SN分布
引理1[1]令f0是一維零對稱概率密度函數,G是一維分布函數,G'存在并且是一個零對稱密度函數,則對任一奇函數w(˙),有

是一個概率密度函數。
由此引理,對任意零對稱密度函數f0,可以通過擾動函數得到一個新的密度函數 f,并且 f0是 f的特殊情況,即取w(x)≡0時。
Azzzlini(1985)取w(y)=αy,α是常數,即得到單變量SN分布。
定義1[1]令Y是一個連續隨機變量,?和Φ是N(0,1)密度函數和分布函數。若Y的密度函數滿足:
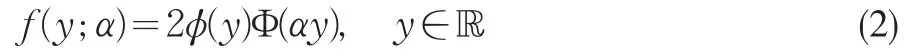
則稱Y服從帶參數a,a∈?,的SN分布,記為y~SN(a)。
稱a,a∈?,為形狀參數,其決定了概率密度函數的形狀,a>0時Y正偏,a<0時Y負偏, ||a增加偏度隨之增加。當a=0時,即N(0,1)。文獻[1]有SN分布與正態分布的關系的研究。
一般的,令Z~SN(a),且Y=ξ+ωZ,其中ξ∈?,ω>0,則Y的概率密度函數是:
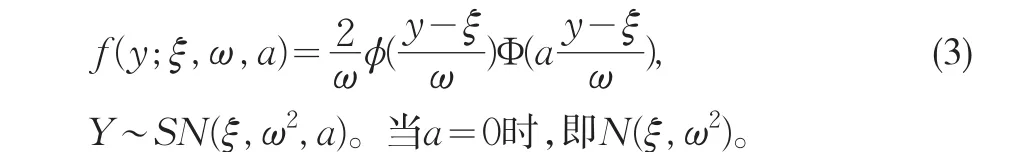
1.2 矩估計
Pewsey(2000,2006)給出SN分布重新參數化后的矩估計,Arellano等(2008)給出重新參數化和原始參數兩種形式下的Fisher信息矩陣。下面綜述文獻[3,4]給出SN分布參數矩估計。
設Y~SN(ξ,ω2,a),則
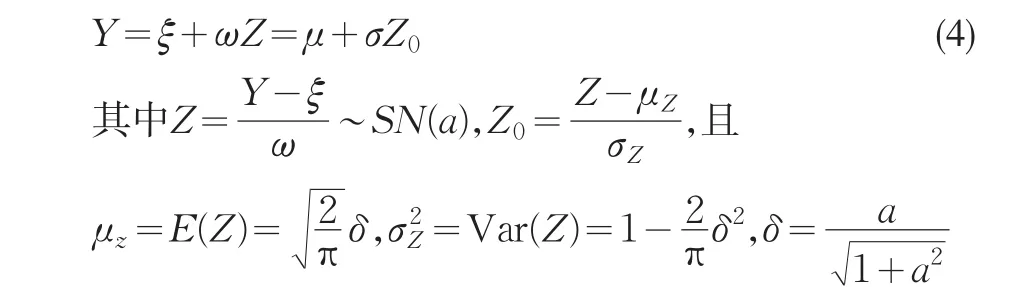
重新參數化后記為(μ ,σ2,γ1),由(4)得
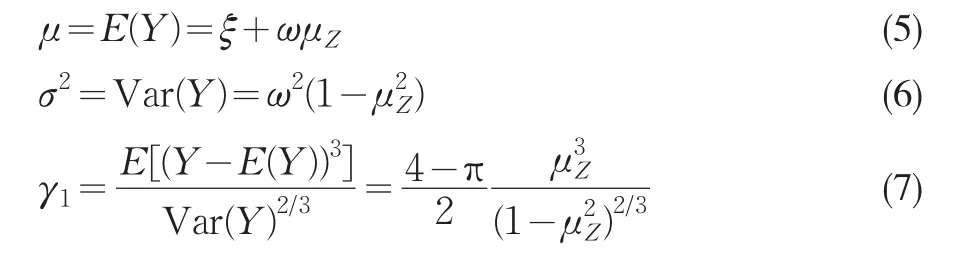
其中γ1表示偏度系數。
解方程(5)(6)(7),得
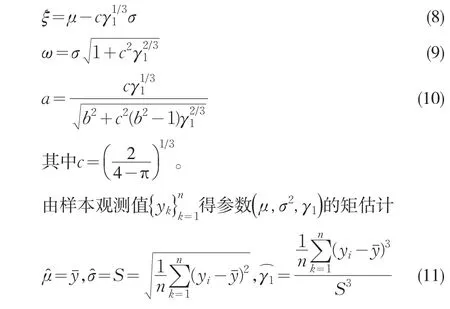
將(11)帶入(8)(9)(10),即得參數(ξ,ω2,a)的矩估計
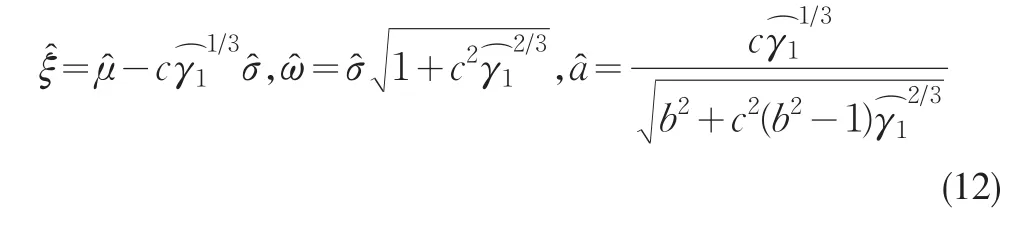
2 SN-ARCH(q)模型
2.1 ARCH模型
定義2(ARCH(q)模型)[5]設是零均值序列無關過程,如果
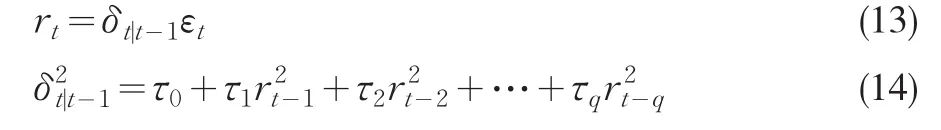
2.2 SN-ARCH模型中位數的無偏估計
Engel(1982)給出ARCH模型參數極大似然估計的Newton-Raphson算法,此算法缺點在于不能保證每一步輸出值非負性;Weiss(1984,)和Ling(2000)分別在四階矩和二階矩條件下給出ARCH模型參數極大似然估計的漸進性質;Lee等(1993)采用得分函數得到模型檢驗;Hong(1996)用譜方法給出ARCH模型的單邊檢驗。Shi等(2003)給出一定條件下的ARCH(0,1)中位數無偏估計[6]。下面構造SN-ARCH(q)的中位數無偏估計。
簡單的,考慮SN-ARCH(1),即

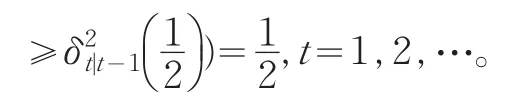
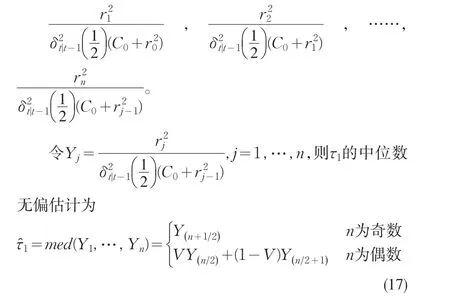
其中V是與Y1,…,Yn獨立的隨機變量,且滿足P(V=0)=P(V=1)=Y(1),…,Y(n)即Y1,…,Yn的次序統計量。
3 實驗結果
基于R統計軟件,對S&P500收益率序列(2001.02.01至2012.02.01,N=3280,0.004±0.0220)在0.05的檢驗水準下進行Bera-Jarque正態性檢驗,拒絕正態分布假設(B-J=1011.000,P<0.001),偏度(Skewness=-0.2320)顯著小于 0。自相關函數以偏離零均值的形式震蕩,以正弦曲線形式緩慢衰減。ARCH-Mcleod-Li殘差檢驗,當殘差平方自相關系數的滯后階數從1到27時檢驗全部顯著(P均小于0.01),存在條件異方差性。建立SN-ARCH模型,模型參數估計如表1所示。

表1 S&P500收益率序列擬合模型參數估計
對上述模型殘差進行McLeod-Li檢驗,殘差及殘差平方序列在多項滯后時的統計結果接受原假設,說明SN-ARCH(1)模型能夠很好的消除原序列的異方差性。
對模型分布進行Pearson擬合優度檢驗[7],比較理論分布與實際分布的接近程度。在0.05的檢驗水平下不拒絕原假設(χ2=31.675,P=0.891),即模型選擇合理。
4 總結與討論
本文從實際序列不服從正態分布的前提假設入手,在ARCH模型中引入SN分布,建立SN-ARCH(q)模型,給出參數中位數無偏估計,實驗結果通過Pearson擬合優度檢驗,證明模型選擇合理。
SN分布的參數估計是比較麻煩的問題,它多了一個參數且密度函數不對稱,因此對于傳統的取對數變換,然后對參數求偏導數,從而得到極大似然估計的方法效果不佳。對于ARCH模型破壞了方差不變的前提假設,故采用了非參數的中位數估計,與傳統的Yule-Walker估計和條件最小二乘估計相比更準確有效。
[1]Azzalini A.A Class of Distribution which Includes the Normal Ones[J].Scand.J.Statist.,1985,12(2).
[2]Shaun A.Bond.A Review of Asymmetric Conditional Density Functions in Autoregressive Conditional Heteroskedasticity Models[Z].2002.
[3]Pewsey A.Modelling Asymmetrically Distributed Circular Data Using the Wrapped Skew Normal Distribution[J].Environ.Ecol.Stat.,2006,(13).
[4]Pewsey A.Problems of Inference for Azzalini,s Skew-normal Distribution[J].J.Appl.Stat.,2000,(27).
[5]Jonathan D.Cryer,Kung-Sik Chan.Time Series Analysis with Applications in R[M].New York:Springer Science Business Media,2008.
[6]Shi N.Z.Wang D.H.Median Unbiased and Maximum Likelihood Estimations of ARCH(0,1)Coefficient[Z].Statistics Simulation and Computation,2003.
[7]Palm F.C.,Vlaar P.J.G.Simple Diagnostics Procedures for Modelling Financial Time Series[J].Allgemeines Statistisches Archiv,1997,(81).

