牛頓迭代算法在聲場定位中的應用

劉 霞，吳 崧

武漢工程大學電氣信息學院，湖北武漢 430205

0 引言

聲場定位技術是確定聲源相對于傳感器的距離和位置的新技術，涵蓋了語言科學、聲學、信號處理、電子學等學科，有著諸多方面的應用.根據聲音探測方式的不同，聲音定位分為主動聲定位和被動聲定位兩種方式［1］.主動聲定位有發射、接收裝置，譬如雷達［2］，使用雷達向外發射信號，然后根據回波的性質判斷待測目標的位置.被動聲定位，只有接收裝置，是利用目標上的輻射信號進行定位，與主動聲定位相比較，具有隱蔽性強、安全性高等特點［3］，是現階段聲音定位技術研究的熱點.

聲場定位系統主要是利用各個傳感器接收聲音信號，經過信號濾波、放大等手段對信號進行處理，然后根據聲音信號到達各個傳感器的時間延時差TDOA(Time Difference of Arrival，以下簡稱:TDOA)計算出聲源相對于傳感器的位置［4］.利用時間延時差計算具體位置的算法有多種，最簡單的就是勾股定律，根據直角三角形三邊關系，計算出聲源相對于傳感器的位置.但是該方法求解方程非常困難，精度不高.牛頓迭代算法是牛頓在17世紀提出的一種在實數域和復數域上近似求解方程的方法，主要針對方程不存在求根公式的情況.牛頓迭代算法是求方程根的重要方法之一，其最大優點是在方程f(x)=0的單根附近具有平方收斂，經過多次迭代，即可計算出結果［5］.

1 系統總體設計

1.1 聲場定位系統的功能設計

本系統在一個矩形區域的4個頂角A、B、C、D分別設置1個傳感器，矩形區域內部設置1個可任意移動的揚聲器，如圖1所示.

圖1 系統結構圖Fig.1 Structure diagram of system

發聲模塊發出特定頻率的聲音信號，傳感器A、B、C、D接收到聲音信號后進行信號濾波、放大等處理，單片機根據處理過的信號計算得到信號到達各點的時間差，再通過特定的算法，即可計算出聲源在矩形區域中的具體位置.

1.2 系統基本原理

基于時間延時差的被動聲音定位算法，其基本原理是在空間內，將4個傳感器分別布置成一定的形狀，來接收聲源的聲音信號，通過計算每相鄰兩個傳感器之間所接收到的信號時間延時差，并結合所布置的聲學陣列的幾何關系，來計算得到聲源位置坐標.如圖2所示的示意圖中，聲源S的位置坐標為(x，y)，聲源S到4個傳感器之間的距離分別為 L1、L2、L3、L4.

圖2 系統坐標示意圖Fig.2 Coordinate schematic diagram of system

2 算法設計

2.1 牛頓迭代算法

設xk是f(x)=0的一個近似根，把f(x)在xk處作泰勒展開可得:

式(1)中若取前兩項來近似代替f(x)，則得到近似線性方程:

利用上述方法，可以將牛頓迭代算法推廣到二元函數，從而對系統的聲源位置坐標求解.

2.2 聲場定位中應用牛頓迭代法

當聲源發聲時，A、B、C、D點會根據聲源S的具體位置按一定先后順序接收到聲音信號，例如點A先收到信號，則B和A之間的時間差為△T1，D和A之間的時間差為△T2.設A點為坐標原點，根據三角函數關系以及聲音在空氣中傳播的時間與距離成正比的關系得到式(4)和式(5):

式(4)和式(5)中，V為聲音在空氣中傳播的速度.設

式(6)和式(7)分別對x，y求偏導數，得:

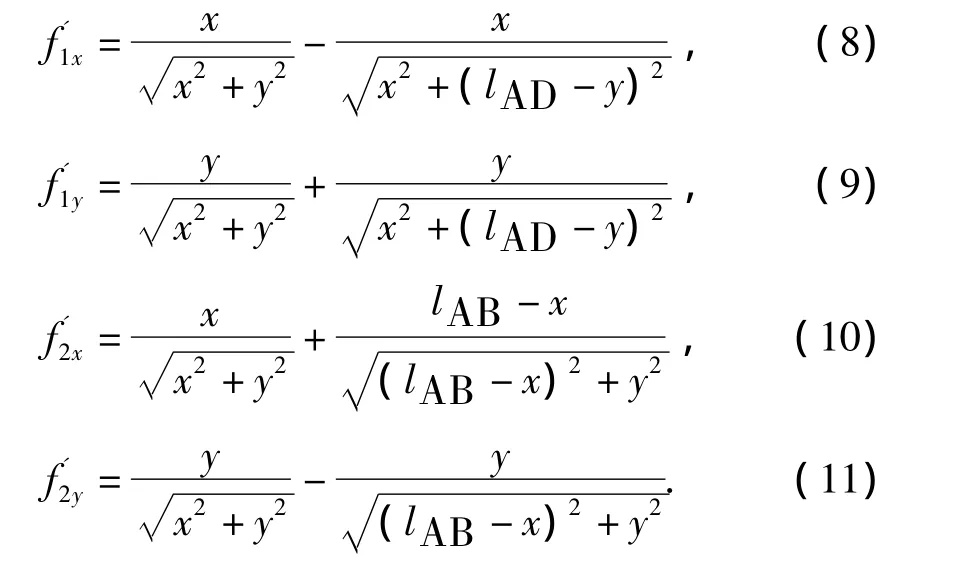
任取一點(x0，y0)，將式(6)和式(7)分別在該點處做泰勒展開，并取其一階導數來近似代替f(x，y)，即 f(x，y)的線性化，得近似線性方程:

式(14)和式(15)，就是求解坐標的迭代公式.在求解過程中，(x0，y0)已知，可以計算出(x，y)的值，再將其帶入以上兩個方程，經過多次迭代運算，即可得到精確的位置坐標.

3 測試與分析

3.1 上位機測試

利用上位機軟件可以很方便的測試牛頓迭代算法的可行性和精確性.編寫的上位機軟件界面如圖3所示.

圖3 上位機界面Fig.3 PC interface

由于是在上位機中進行模擬測試，所以需要設定S點到A、B、C、D點的距離數據和時間延時差△T1，△T2用于算法的測試.實驗中，給定待測坐標為(30，80)，生成測試所需的數據為L1=85.44，L2=476.76，L3=542.033，L4=271.662，△T1=1.150 94，△T1=0.547 1.點擊“求解”按鈕進行迭代運算，位置坐標結果見表1.

表1 上位機測試數據Table1 Test data of computer

從表1可以看出，只需經過3次迭代運算，即能精確得到待求的位置坐標，并且在第1次迭代運算時，得到的數據就已經非常接近實際值.

3.2 實物測試

在350 mm×500 mm的坐標紙上進行測試，傳感器位于矩形區域的4個頂角，聲源模塊位于矩形區域內，讓聲源發出1 s左右的聲音信號，單片機接收信號并進行運算.編寫單片機程序用于實物測試，圖4為系統軟件流程圖.

圖4 程序流程圖Fig.4 Diagram of program flow

經過多次試驗所得結果如表2所示.

表2 實物測試數據Table 2 Test data

試驗表明，系統能夠可靠的實現坐標定位，但是略有誤差.這種誤差大多來源于傳感器后級的信號處理，若4個信號處理部分不能完全一致，則時間延時差就不能準確測量，從而導致誤差的存在.但是定位精度仍能達到±15 mm，可見定位性能穩定可靠.

4 結語

筆者提出了一套被動定位方式的聲場定位系統，利用聲音到達的時間延時差進行處理對聲源進行精確定位.由于聲音頻率的局限性以及室內具體因素的影響，目前只能用在聲音干擾小的環境且聲源聲音頻率單一的情況.但系統采用的牛頓迭代算法，具有非常強的實用性.利用牛頓迭代算法的快速收斂性，在迭代過程中，只需要迭代幾次就可以快速、精確計算得到聲源坐標.上位機模擬測試和實物測試表明，牛頓迭代算法在聲場定位中有著重要的應用價值.

［1］吳曉，靳世久，李一博.基于麥克風陣列聲音信號定位方法的研究［J］.傳感器技術學報，2010，5(23):682-684.WU Xiao，JIN Shi-jiu，LI Yi-bo.Sound source localiza-tion based on microphone arrays［J］.Chinese Journal of Sensors and Actuators，2010，5(23):682-684.(in Chinese)

［2］ADAMY D.Radar warning receivers:the digital revolution［J］.Electronics Defense，2000(6):45-49.

［3］肖峰，李惠昌.聲，武器和測量［M］.北京:國防工業出版社，2002.XIAO Feng，LI Hui-chang.Sound，weapons and measurement［M］.Beijing:National Defence Industry Press，2002.(in Chinese)

［4］陳益如，王博，鄔楊波.基于聲音導引的聲源定位系統設計［J］.工業控制計算機，2010，23(10):101-104.CHENG Yi-ru，WANG Bo，WU Yang-bo.Design of sound source localization system based on voice guidance ［J］.The Industrial Control Computer，2010，23(10):101-104.

［5］徐瑞民.二元非線性方程組求根的牛頓迭代法［J］.山東輕工業學院學報，2009，23(4):80-91.XU Rui-min.Newton’s method fourth-nonlinear function of two independent variables［J］.Journal of Shandong Institute of Light Industry，2009，23(4):80-91.(in Chinese)