基于Copula函數的水文變量條件組合分析

劉和昌，梁忠民，姚 軼，唐甜甜

（河海大學水文與水資源學院，江蘇 南京 210098）

0 引 言

目前，在水文計算中采用的多是特定組合的分析方法，如最不利組合、同頻率組合等。理論上，進行多變量的組合分析計算，必須給出變量間的聯合概率分布函數。目前，應用最廣泛的是多元正態聯合分布；但其針對的是各變量邊際分布為正態分布的情形。非正態分布，原則上需要對變量進行正態化變換，變換過程復雜且會使一些信息失真，限制了其使用范圍。

近年來興起的基于Copula函數的多維聯合分布理論[1]，將變量間的聯合分布分解為變量間的相關性結構和變量的邊緣分布，為構建多變量聯合分布提供了有力的數學分析工具。由于Copula函數對變量的邊際分布線型沒有任何限制，而且聯合分布函數可以解析表達，所以在水文領域中得到了較廣泛的研究和應用。Favre等[2]首次利用Copula函數研究了洪水地區組成及峰量組成的計算問題；Poulin等[3]針對多變量頻率分析中的尾部相關，研究了Copula函數的選型問題；肖義等[4]應用Copula計算洪水峰、量聯合分布，以并集聯合分布概率為設計標準作為控制，由此對典型洪水過程線進行放大，獲得設計洪水過程線；郭生練等[5]對copula函數在水文中研究與應用的進展進行了評述和總結；張娜等[6]通過Copula函數分別構建最大日雨量與最大時段雨量的聯合分布，以推求設計暴雨過程；閆寶偉等[7]根據Copula聯合分布的條件期望組合概念，研究了設計洪水的地區組成計算方法；梁忠民等[8]采用三變量Copula函數，分析了三峽水庫預泄對鄱陽湖防洪的影響。

本文基于Copula函數推導了條件最可能組合的計算公式，并對錢塘江水系的4個站點洪水頻率進行了分析計算，提供了不同設計標準條件下最可能組合的峰、量設計值及其90%的置信區間，并與同頻率組合及條件期望組合的結果進行了對比分析。

1 Copula函數和條件組合

1.1 Copula函數

Copula函數是定義域為[0，1]均勻分布的多維聯合分布函數，二維Copula函數為[1]

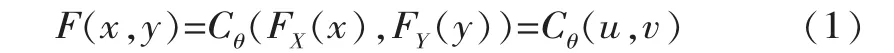
式中，C為Copula函數；θ為Copula的參數；u=FX（x），v=FY（y）分別為隨機變量X和Y的邊緣分布。相應的聯合概率密度函數為

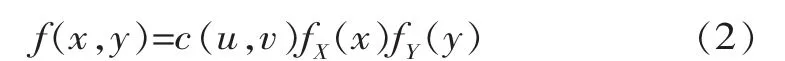
式中，c（u，v）為Copula函數的密度函數；fX（x）和fY（y）分別為隨機變量X和Y的概率密度函數。

在水文領域，兩個變量單參數Archimedean Copula函數簇應用最為廣泛，Gumbel-Hougaard Copula函數即為其中一種。Gumbel-Hougaard Copula函數適于變量間存在正相關的情形，并且能描述變量間的上尾相關性[3]，故本文選用Gumbel-Hougaard Copula作為聯合分布函數，其表達式為

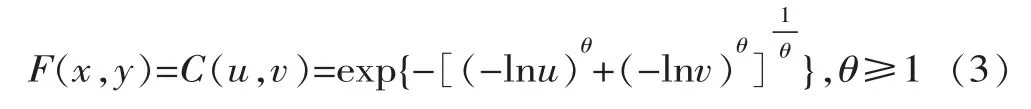
其密度函數為

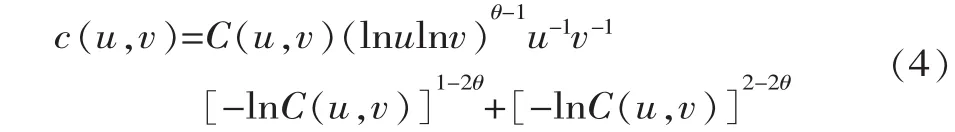
函數參數θ與Kendall秩相關τ系數間關系如下

采用離差平方和準則 （OLS）來評價Copula方法的擬合度

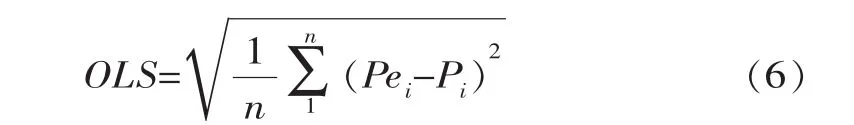
式中，Pei和Pi分別為經驗頻率和理論頻率。

1.2 邊緣分布

隨機變量X和隨機變量Y均采用P-III分布，則其概率密度函數

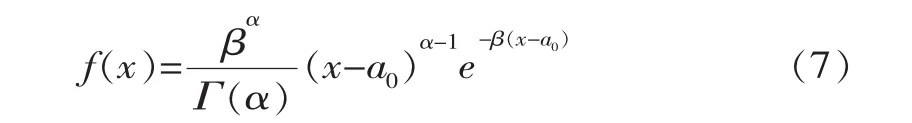
式中，Γ（α）為伽瑪函數；α、β和a0分別為形狀、尺度和位置參數。

隨機變量X和隨機變量Y的分布函數

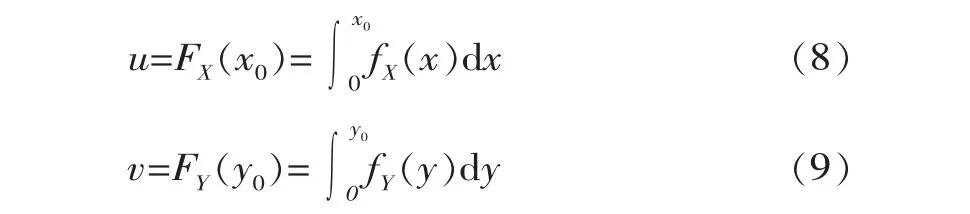
式中，x0和y0為大于0的任一值；fX（x）和fY（x）分別變量X和變量Y的概率密度函數。

1.3 條件組合

1.3.1 條件最可能組合

當變量X取設計值xp時，變量Y所對應的值并非唯一，可大可小，只是出現不同值的概率不一樣，即存在一個條件概率分布

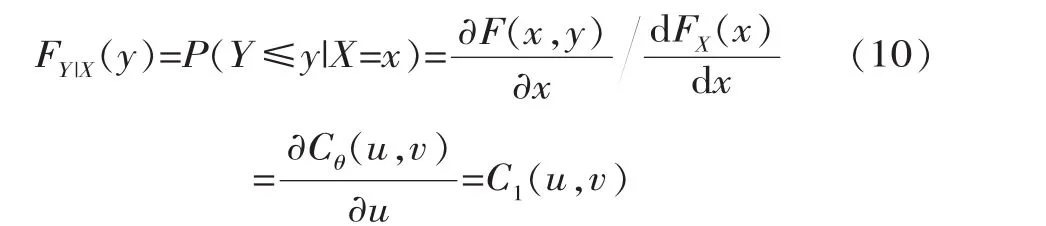
此時，FY|X（y）的密度函數fY|X（y）=c（u，v）fY（y），而當fY|X（y）取最大值時對應的yM值所形成組合（xp，yM），即為條件最可能組合。fY|X（y）為y的一元函數，將密度函數fY|X（y）對y求導，得

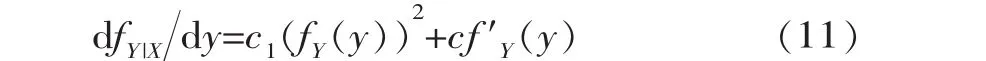
式中，c1=?c（u，v）/?v，c、u、v定義同上。 再令dfY|Xdy=0，整理得:

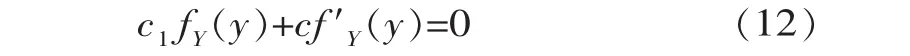
求解式（12），可得x取xp時，y的最可能取值yM。

1.3.2 條件期望組合

本節中，在給定變量X的值為xp時，y的期望值E（y|xp）對應的組合（xp，E（y|xp））即為條件期望組合[7]。其中，E（y|xp）的計算如下:

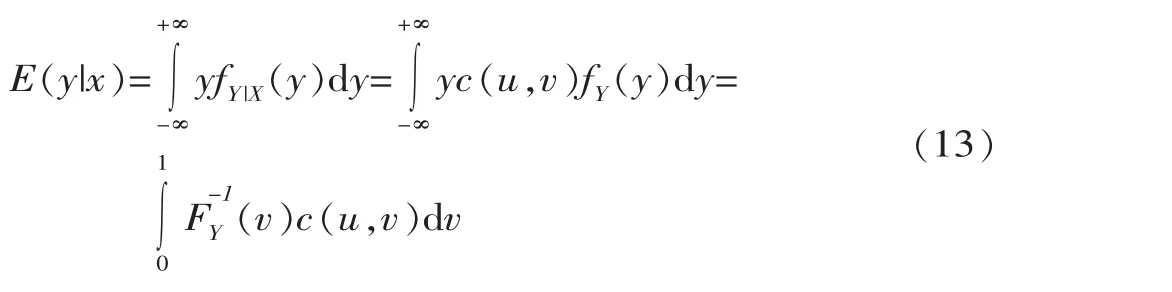
式中，fY|X（y）=c（u，v）fY（y），為FY|X（y）的密度函數；（v）為v=FY（y）的反函數。

變量X取值為xp時，若令FY|X（y）分別等于α/2和1－α/2，求得的Y值分別為yl和yu；則已知xp時y的1－α的置信區間為[yl，yu]。

2 實例分析

以錢塘江湖南鎮、黃壇口、新安江和富春江4個站點40年的洪水資料為例，對本文所提方法進行應用分析，其中湖南鎮、黃壇口、新安江位于錢塘江支流上，富春江位于干流上。洪峰和時段洪量均按服從P-III型曲線分布，采用線性矩法估計分布參數，各站點年最大洪峰 （m3/s）和時段洪量 （億m3）統計參數估計結果見表1；洪峰和時段洪量間的Kendall秩相關系數τ由式（5）計算，其結果及對應的OLS值見表2。

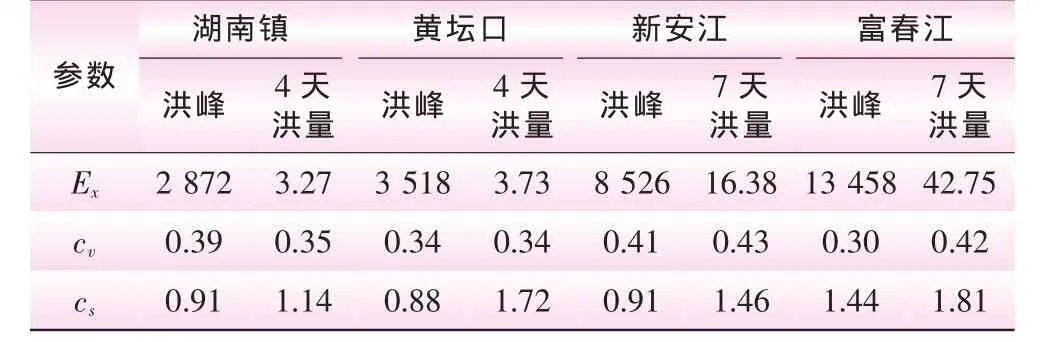
表1 各站點統計

表2 各站點τ值和OLS值

以富春江站為例，通過給定不同洪峰值，由式（12）和式 （10）可分別求得對應的7天洪量條件最可能值和90%的置信區間。為了對比分析，也提供了條件期望值及同頻率值的估計結果 （見圖1，2及表3，4）。

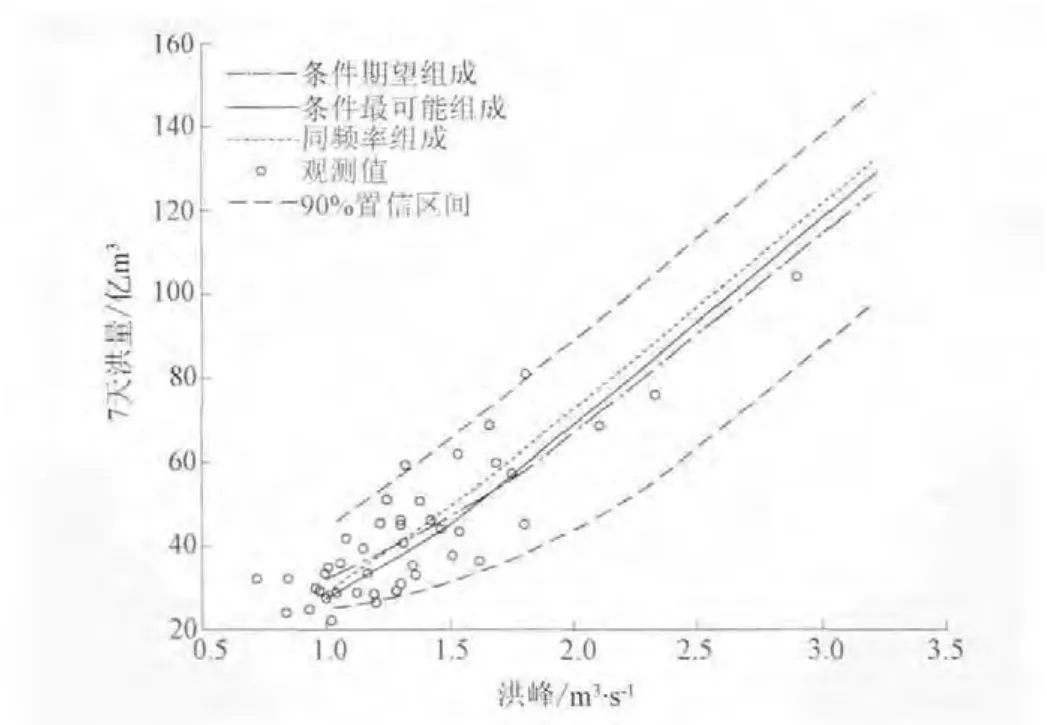
圖1 富春江站以洪峰為條件的7天洪量估計結果

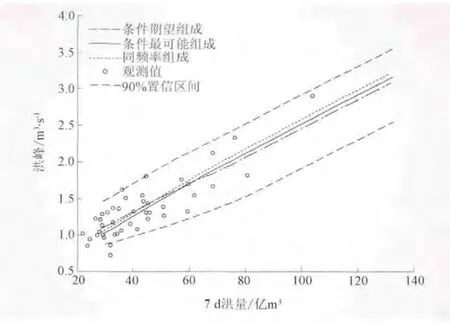
圖2 富春江站以7天洪量為條件的洪峰估計結果

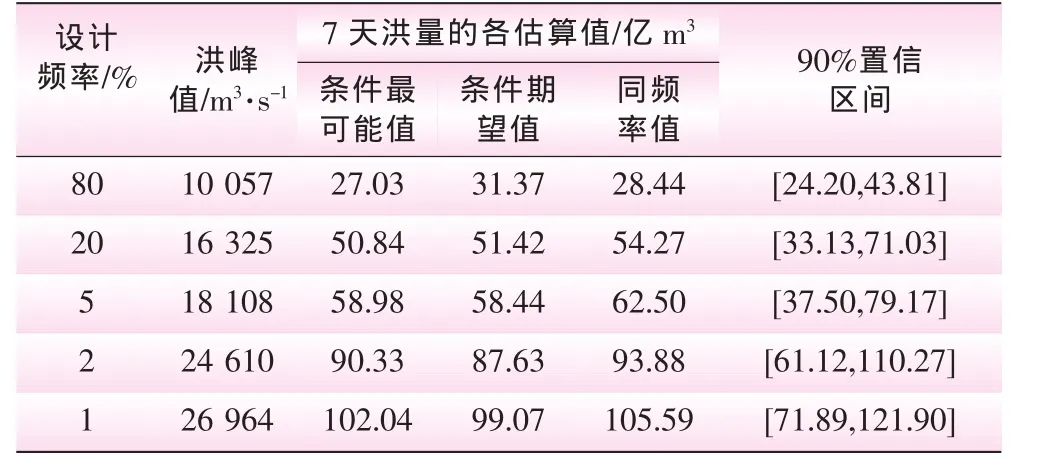
表3 富春江站以洪峰為條件的7天洪量的各種估計值

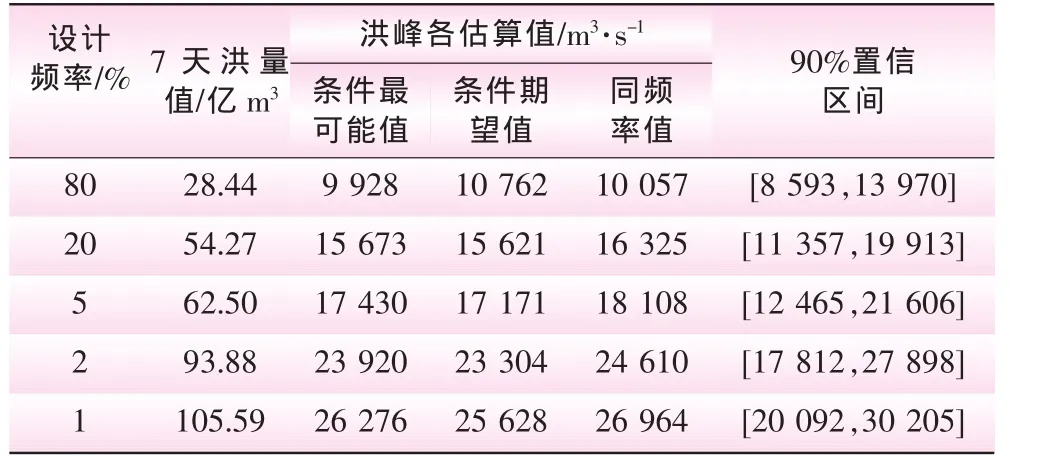
表4 富春江站以7天洪量為條件的洪峰的各種估計值

考慮洪峰與7天洪量之間的相關性，條件最可能組合是給定洪峰值 （或7天洪量）時，7天洪量（或洪峰）取值的最可能情況，條件期望組合則代表的是其取值的平均情況，兩種組合方法均具有一定的統計基礎；一般認為，目前常用的同頻率組合法是一種更偏安全或保守的方法。

由圖1～2可知，富春江站，在給定洪峰值情況下，以設計頻率等于17%為界 （對應約6年一遇重現期），當其小于17%時，7天洪量的條件最可能值介于同頻率值與條件期望值之間，同頻率值最大；在給定7天洪量情況下，當設計頻率小于25%時（對應4年一遇重現期），洪峰的條件最可能值位于同頻率值和條件期望值之間，同頻率值最大。因此，對富春江站而言，當設計標準超過6年一遇時，按照最可能組合條件計算的峰、量設計值，其數值介于按同頻率組合與條件期望組合的估值之間，同頻率組合的估值最大。

湖南鎮、黃壇口和新安江3個站，也作了上述分析計算，結果類似。其中，湖南鎮的設計頻率臨界值為25%，黃壇口的為14%，新安江的為29%，即當其設計頻率小于該值時，按照最可能組合條件計算的峰、量設計值，其數值介于按同頻率組合與條件期望組合的估值之間；另外，估計結果也表明，同頻率組合的估值均是最大的。

因此，可以初步認為，對于錢塘江水系，當設計頻率小于14%時 （對應于8年一遇以上的重現期），同頻率組合方式計算的設計洪水大于條件期望組合和條件最可能組合的結果。對于水庫工程而言，其設計標準一般都是較高的，如百年一遇、千年一遇等；所以按照同頻率組合的設計成果一般都是偏于安全的。本文的研究表明，最可能組合計算的設計值介于同頻率組合與期望組合的設計值之間。

3 結 論

（1）在聯合分布的基礎上，推導了條件最可能組合的計算公式，為計算峰、量條件最可能設計值提供了基礎。

（2）對錢塘江水系4個站點的洪水頻率分析結果表明，按照最可能組合條件計算的峰、量設計值，其數值介于按同頻率組合與按條件期望組合的估值之間。由此也證明了，目前的同頻率法設計洪水計算成果一般是偏于安全的。

（3）條件最可能組合代表的是變量間的一種最可能遭遇出現的方式，較適合于水文事件的組合情況，但本文的結果僅是初步的，值得作進一步研究。

［1］NELSON R B.An introduction to Copulas［M］.New York:Springer,1999.

［2］FAVRE A-C,ADLOUNI S E,PERRAULT L,et al.Multivariate hydrological frequency analysis using Copulas［J］.Water Resource Research,2004,40（1）,W01101.

［3］POULIN A,HUARD D,FAVRE A C,et al.Importance of tail dependence in bivariate frequency analysis［J］.Journal of Hydrologic Engineering,2007,12（4）:394-403.

［4］肖義，郭生練，劉攀，等.基于Copula函數的設計洪水過程線方法［J］.武漢大學學報: 工學版，2007，40（4）:13-17.

［5］郭生練，閆寶偉，肖義，等.Copula函數在多變量水文分析計算中的應用及研究進展［J］.水文，2008，28（3）:1-7.

［6］張娜，郭生練，肖義，等.基于聯合分布的設計暴雨方法［J］.水力發電，2008，34（1）:18-21.

［7］閆寶偉，郭生練，郭靖，等.基于Copula函數的設計洪水地區組成研究［J］.水力發電學報，2010，29（6）:60-65.

［8］梁忠民，郭彥，胡義明，等.基于Copula函數的三峽水庫預泄對鄱陽湖防洪影響分析 ［J］.水科學進展，2012，23（4）:485-492.