粗粒料二維與三維孔隙率的對應關系研究
何詠睿 ,朱 晟 ,2,武利強 ,2
(1.河海大學水工結構研究所,江蘇 南京 210098;2.河海大學水文水資源與水利水電工程科學國家重點實驗室,江蘇 南京 210098)
0 引 言
近年來我國高土石壩發展十分迅速,粗粒料作為土石壩的主要材料,其力學特性對壩體的變形有著決定性的影響。對粗粒料進行二維數值試驗時,孔隙率是影響粗粒料力學性質的重要因素,對粗粒料的強度與變形均有很大的影響。為使二維數值試驗中的二維模型與模擬的三維實體力學性質等價,必須實現二維模型的孔隙率與三維實體的等價。現今常用的二維與三維孔隙率轉換公式是由等粒徑顆粒體組成的結構推導而出,僅用密實度進行修正,未考慮粒徑分布對孔隙率的影響[1-3],無法實現二維模型孔隙率和實體的三維孔隙率完全等價。鑒于此,本文參考不同土石壩工程的粗粒料級配,設計一系列具有代表性的級配組,對每組用二維顆粒流程序(pfc2d)和三維顆粒流程序 (pfc3d)模擬極值孔隙率試驗,統計出不同級配下二維與三維極值孔隙率,探討粒徑分布及壓實程度對二維與三維孔隙率轉換關系的影響,擬合出二維與三維孔隙率的轉換公式,并與常用的轉換公式進行比較。
1 數值試驗的級配確定
土石壩為當地材料壩,受料場原生條件的限制,不同工程所用粗粒料級配差異較大。為了使所選用的級配曲線組具有代表性,探尋不同工程粗粒料級配的共有特征,在采用重型振動碾進行薄層碾壓施工的工程中,粗粒料的級配設計均以talbot曲線[4]為母線。
參照水布埡和三板溪[5-6]等工程級配設計方法,以talbot曲線為母線設計試驗級配。根據DL/T 5356—2006《水利水電工程粗粒土試驗規程》,選定最大粒徑為60 mm,引入分形維數定義talbot曲線形狀指數[7],設置分形維數n分別為2.7、2.6、2.5、2.4、2.3、2.2、2.1、2.0,所得的級配曲線組見圖1。曲線組構成的區域幾乎涵蓋現代采用連續級配理論設計的堆石壩進行數值試驗的級配。因此,根據這組級配研究得到的規律適用于現代及今后按連續級配理論設計的堆石壩粗粒料的數值試驗研究中。
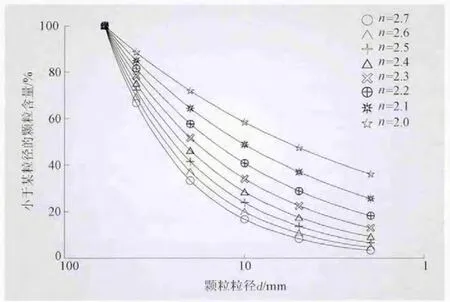
圖1 各分形維數下的級配
2 數值試驗
2.1 顆粒流程序模擬粗粒料極值孔隙率試驗的可行性分析
由等粒徑顆粒結構推導出的常用二維與三維孔隙率轉換關系為[3]
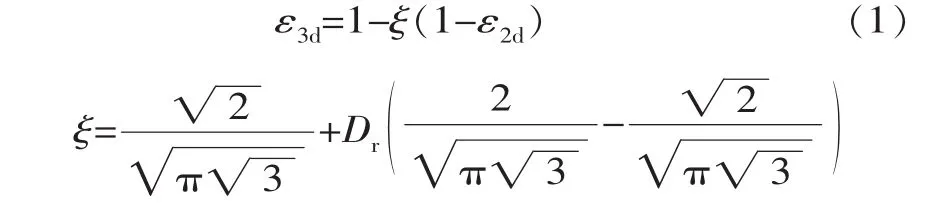
式中,ε2d為二維孔隙率;ε3d為三維孔隙率;ξ為修正系數;Dr為相對密度。
用pfc2d和pfc3d模擬等粒徑顆粒料的極值孔隙率試驗,校驗得出的二維與三維孔隙率是否符合公式(1),以此決定研究方案的可行性。為加快計算速度,pfc2d數值模擬中設置顆粒直徑為0.005 m、2000個;pfc3d中設置顆粒直徑為0.005 m、5000個。將pfc2d模擬極值孔隙率試驗后得出的極值孔隙率按公式(1)轉換成三維孔隙率,與pfc2d、pfc3d模擬極值孔隙率試驗得到的極值孔隙率統計于表1。表1中,按公式轉換得到的三維孔隙率與pfc3d模擬得到的孔隙率非常近似,證明用顆粒流程序模擬極值孔隙率試驗探究二維與三維孔隙率轉換關系的方案可行。

表1 等粒徑顆粒組的二維、三維極值孔隙率
2.2 pfc模擬極值孔隙率試驗
2.2.1 試驗參數的確定
數值試驗參數通過一組硅質巖堆石料三軸試驗曲線反算調整獲得[8-9],數值試驗的細觀參數見表2。其中,Kn、Ks分別為顆粒的法向及切向接觸剛度;f為顆粒間摩擦系數。

表2 數值試驗的細觀參數
2.2.2 數值模擬步驟
(1)建立邊界:在pfc3d中建立底半徑為0.15 m,高為0.34 m的圓筒模型。在pfc2d中建立寬為0.3 m、高為0.34 m的矩形模型。
(2)制樣:在邊界中根據設計的級配曲線制樣,按照水利水電實驗規程,粗粒料按60~40、40~20、20~10、10~5 mm以及5 mm以下進行粒組篩分,但依此生成顆粒后發現pfc3d中顆粒數目達幾十萬個,遠遠超出電腦負荷。因此,將5 mm以下的顆粒全部用5~10 mm顆粒進行等質量替換。
(3)模擬松填法求最大孔隙率:顆粒在重力作用下自由下落,通過控制顆粒速度確保顆粒落距2~5 cm,顆粒下落穩定后為最大孔隙率狀態。
(4)模擬振動臺法求最小孔隙率:在顆粒表面置加重底板,使其對顆粒產生14 kPa的平均壓力。設定底部墻體運動方程為正弦曲線,振幅為0.002 m,頻率為251.3 rad/s,模擬振動臺振動,追蹤配位數變化,穩定后停止振動,顆粒達到最密實狀態。
(5)卸除加重底板,顆粒釋放應力自由回彈后為最小孔隙率狀態。
2.2.3 模擬結果
根據公式(1),將pfc2d數值模擬得到的孔隙率換算成三維孔隙率,與pfc2d、pfc3d模擬得到的極值孔隙率統計于表3。
3 結果分析
3.1 數據有效性分析
從表3看出,三維孔隙率均大于二維孔隙率,這是由于二維模型中假定所有的顆粒球心均處在一個平面上,而實際三維實體中顆粒球心無規律分布于空間,更容易形成 “弓形”架構。
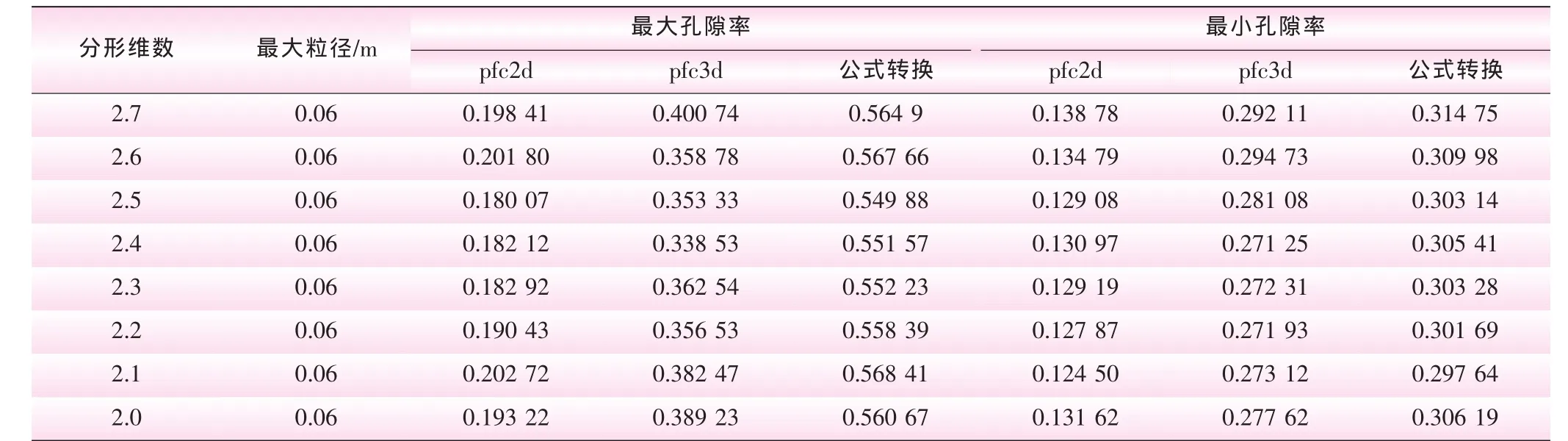
表3 各級配的極值孔隙率
由于pfc3d運算對顆粒數目的限制,制樣中簡化了0~5 mm的顆粒,不可避免地給極值孔隙率值帶來一定誤差。表3中,分形維數由2.7減至2.0,極值孔隙率總體上呈先減后增的趨勢,在分形維數為2.5左右達到最小,這與Ochiai M等[10]得到的規律相吻合。本文旨在探究粗粒料的二維與三維極值孔隙率轉換關系,pfc2d與pfc3d數值試驗中粗粒料級配的簡化是同步的,且所得數據符合實際規律,故得到的轉換關系是可靠的。
3.2 擬合公式
繪制pfc數值試驗得到的三維孔隙率關于二維孔隙率的散點圖 (見圖2),將二維極值孔隙率按公式 (1)換算得到三維孔隙率,在圖2中繪入公式換算得到的三維孔隙率與二維孔隙率對應點。圖2中,按照公式換算得到的三維孔隙率較pfc3d模擬得到的均偏大,且在Dr=0.0時相差較大。這是由于公式 (1)由等粒徑顆粒體推導而來,僅用相對密度進行修正,忽略了粒徑分布對孔隙率的影響,而級配良好的顆粒堆積體孔隙率明顯小于級配差的,故按照公式計算的孔隙率均大于pfc3d模擬得到的。
對不同分形維數下二維與三維極值孔隙率進行相關性分析可知,二維與三維極值孔隙率呈高度線性相關,相關系數達0.94,可用直線y=1.4618x+0.08794擬合,并繪制擬合直線于圖2中。顯然,相比于公式 (1),該直線能更好地反應粗粒料二維與三維極值孔隙率的關系,且相對密度分別為0.0與1.0時,二維與三維孔隙率的對應點分別密集分布在直線的 x=0.12~0.14、0.18~0.20段。由此推測,其他相對密度下粗粒料二維與三維孔隙率對應點會密集分布在0.14~0.18段,但需進一步證實。
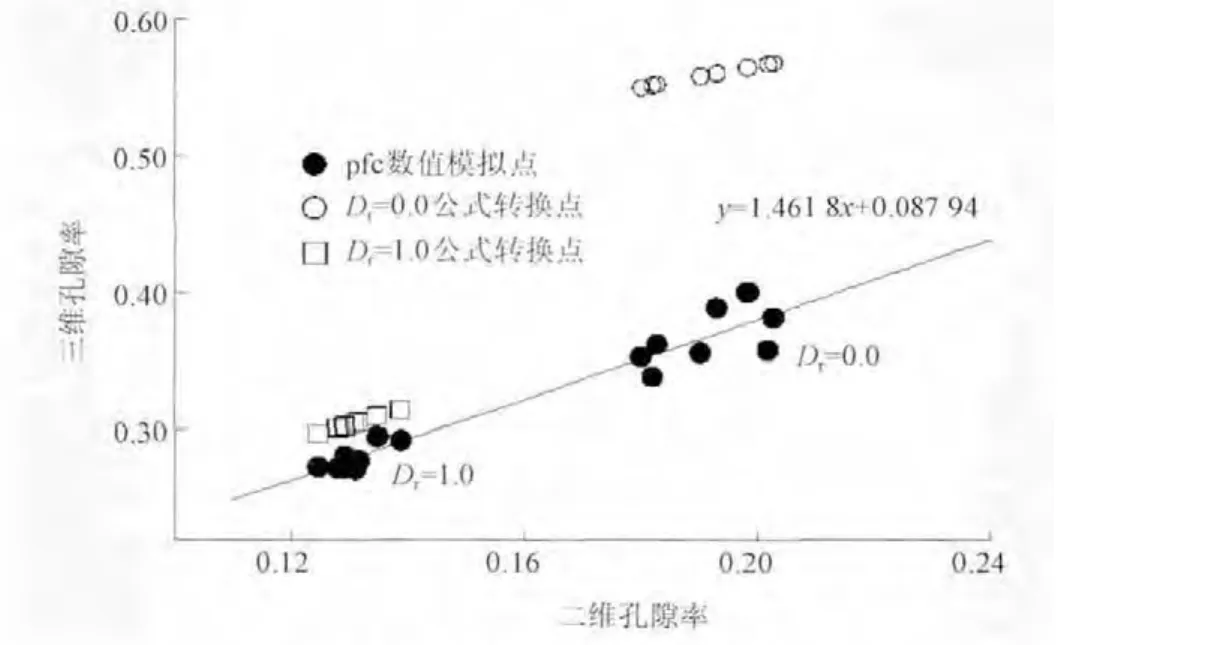
圖2 二維與三維孔隙率對應點
4 結 論
通過設計一系列具有代表性的粗粒料級配,用pfc2d、pfc3d模擬極值孔隙率試驗探究粗粒料二維與三維孔隙率的對應關系,得出如下結論:
(1)實際三維結構比二維模型的孔隙率大。二維模型假定所有的顆粒球心均處在一個平面上,而三維結構中顆粒球心無規律分布于空間中,更易形成 “弓形”架構,故孔隙更大。
(2)相同壓實度下,等粒徑顆粒體比級配良好的顆粒體的孔隙率大。根據常用二維與三維孔隙率轉換公式求得的三維孔隙率會大于實際三維孔隙率,且在相對密度為0時相差較大。
(3)設計級配下,粗粒料的二維極值孔隙率與三維極值孔隙率呈高度線性相關,用直線擬合后具有良好的歸一性。相對密度分別為0.0與1.0時,二維與三維孔隙率的對應點分別密集分布在直線的兩段,推測其他密實度下二維與三維孔隙率對應點也會密集分布在該直線的某段,但需進一步研究證實。
(4)本次數值試驗探究粗粒料的二維與三維孔隙率對應關系,沒有考慮粗粒料的顆粒形狀和破碎的影響,考慮顆粒形狀和破碎后粗粒料的二維與三維孔隙率對應關系尚待進一步探究。
[1]MITCHEL J K.巖土工程土性分析原理[M].高國瑞,譯.南京:南京工學院出版社,1988.
[2]日本土質工學會.粗粒料的現場壓實[M].北京:水利水電出版社,1999.
[3]張剛.管涌現象細觀機理的模型試驗與顆粒流數值模擬研究[D].上海:同濟大學,2007.
[4]王永明,朱晟,任金明,等.筑壩粗粒料力學特性的縮尺效應研究[J].巖土力學,2013,34(6):1799-1807.
[5]李昌彩.水布埡面板堆石壩前期關鍵技術研究[M].北京:水利水電出版社,2005.
[6]趙海斌.超硬巖筑壩材料現場爆破與現場碾壓試驗研究[R].長沙:中國水電顧問集團中南勘測設計研究院,2006.
[7]朱晟,武利強,魏匡民,等.一種基于分形理論的粗粒料縮尺方法: 中國,CN103134906A[P].2013-06-05.
[8]王永明,任金明,武利強,等.pfc模擬筑壩粗粒料力學特性的有效性分析[J].水電能源科學,2012,30(10):72-75.
[9]周健,池毓蔚,池永,等.砂土雙軸試驗的顆粒流模擬[J].巖土工程學報,2000,22(6):701-704.
[10]OCHIAI M,OZAO R,YAMAZAKI Y,et al.Self-similarity law of particle size distribution and energy law in size reduction of solids[J].Physica A:Statistical Mechanics and its Applications,1992,191(2):295-300.

