基于EMD-FFT的水電機組振動信號檢測

陳喜陽，閆海橋，孫建平

（華中科技大學能源與動力工程學院，湖北 武漢 430074）

0 引 言

水電機組設備在運行中不斷受到機械或電氣損傷，過流部件還經歷空蝕破壞、泥沙磨損及尾水渦帶、周期性脫流和卡門渦等水力激振力作用，振動信號可能是由機械、水力或電磁中的某一個因素產生的，也可能是由多個因素耦合作用引起的綜合結果，體現出明顯的非平穩特性[1-2]。為了對水電機組故障展開診斷，有必要提取與物理作用對應信號的動態特征，捕捉非平穩振動信號中與振源對應的突變成份時頻征兆。當前水電機組振動信號分析方法依然立足于傳統的FFT（快速傅立葉變換算法），從時域變換到頻域時，丟失了時間信息，僅能求解到整體信號的頻譜，無法確認各頻率成份發生時刻，難以把握非平穩信號的局部細節信息，容易造成對機組實際運行性能的誤判。

如何有效同時提取非平穩信號時域與頻域特征，一直是信號處理領域的研究熱點。Dennis Gabor提出了短時傅立葉變換,先用一個在有限區間外恒為零的光滑函數去乘所需分析的信號，再進行FFT，得到信號的局部特性，但所加窗口形狀大小固定不變，使其在實際應用中受限制，效果不夠理想[3]。EMD（empirical mode decomposition）經驗模態分解作為一種自適應分解方法，在不同趨勢或尺度上對原始信號逐層展開分解，衍生一序列的本征模函數（intrinsic mode function，IMF），通過對 IMF 分量進行Hilbert變換，獲取該信號的時間-瞬時頻率-瞬時幅值的特征分布[4]。EMD與傳統FFT本質區別在于不需設定任何基函數，僅依據信號的局部特征尺度，自適應的對非平穩信號進行平穩化處理，已在旋轉機械振動信號分析領域得到了應用。文獻[4]對滾動軸承振動信號EMD分解，產生IMF分量，計算各IMF信息熵，設定熵閾值取舍IMF分量，對重構信號進行Hilbert包絡譜分析，診斷實例驗證該方法捕捉了軸承故障的特征頻率。文獻[5]將EMD分解后的IMF，進一步細分為包絡和純調頻信號，然后對純調頻信號反余弦求取瞬時頻率，獲得了振動信號頻率和幅值隨時間動態變化趨勢。文獻[6]對水電機組擺度信號EMD分解產生的各IMF分量進行FFT，提取了擺度信號中蘊含的微弱渦帶信息。文獻[7]采用EMD與指標能量理論，提取了水電機組尾水管動態特征，可識別渦帶是否發生及嚴重程度。EMD在上述應用實例中，均能有效捕捉到信號的時間信息以及頻率信息，但由于缺乏嚴格的正交性，使得各IMF分量出現模態混淆現象，不同分量中通常包含頻率相近的信號，導致分解結果的時間-瞬時頻率-瞬時幅值中瞬時幅值出現失真而造成誤判[8]。

針對上述狀況，本文提出了一種融合FFT和EMD經驗模態分解的EMD-FFT時頻分析方法，算法思想為:利用EMD時頻聚焦性，自適應的將原始信號進行平穩化分解，從IMF分量中捕獲非平穩信號的突變成份發生時段，并通過FFT獲得該時段原始信號的頻率與幅值信息，準確獲取了非平穩信號的時間-瞬時頻率-瞬時幅值。仿真算例和水電機組振動分析實例表明，EMD-FFT克服了FFT丟失了時間信息和EMD中所得幅值信息不準的缺陷，可有效的捕捉突變信號的時間-瞬時頻率-瞬時幅值特征量，為水電機組非平穩振動信號檢測提供了一種新時頻分析方法。

1 EMD-FFT時頻分析方法

EMD-FFT根據非平穩信號自身的局部時間特征尺度，自適應按照頻率從高到低分解為若干IMF本征模函數序列，實現了非平穩信號在不同尺度或趨勢上的平穩化處理過程，捕捉突變信號發生時刻，并對該時段的原始信號進行FFT分析，最終檢測到該非平穩信號的時間-瞬時頻率-瞬時幅值特征量。EMD-FFT實質是利用EMD經驗模態分解精準地捕獲突變信號的時域信息，并結合FFT獲取頻率及幅值信息，算法流程如下:

（1）計算原始信號x（t）所有極大值點和極小值點。

（2）運用三次樣條曲線插值擬合出x（t）的上、下兩條包絡曲線。

（3）求取x（t）上、下包絡線的均值，記為μ，然后用 x（t）減去 μ，得到剩余分量 h（t）=x（t）-μ。

（4）判斷h（t）是否滿足IMF的兩個條件:在所有的數據序列中，極值點的個數與過零點的個數相等或者最多相差一個；所有的極大值點確定的上包絡線與所有的極小值點確定的下包絡線的平均值為零。若h（t）不滿足IMF條件，將其作為原始數據即x（t）=h（t），重復以上步驟 （1） 到 （4），直到得到一個IMF； 否則，將h （t）作為x（t）的一個IMF分量，即 c（t）=h（t）。

（5） 將 c（t）從 x（t）中分離出來，得到的剩余分量 r（t）作為原始數據，重復以上步驟（1）到（5），直到r（t）只有一個極值點為止，此時r（t）為殘余分量。

（6） 原始信號通過上述（1）到（5）變換后，實現了非平穩信號在不同頻率或趨勢上的平穩化處理過程，繪制所有的IMF波形圖，確定突變信號成份所對應的時段，獲取該突變信號時間信息。

（7）通過FFT計算該時段原始信號的頻率與幅值信息，綜合EMD所獲得的時間信息，最終提取非平穩信號的時間-瞬時頻率-瞬時幅值特征量。

2 仿真算例

為了驗證EMD-FFT在檢測非平穩信號動態特性的效果，下面以一個仿真的振動信號為例，說明EMD-FFT時頻分析的具體實施過程，并與單一的FFT分析及EMD分析結果對比。仿真信號解析表達式為:

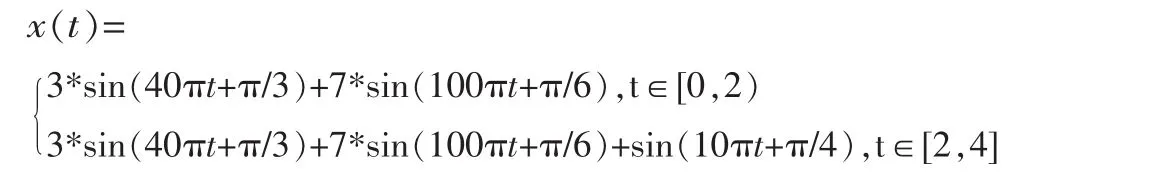
由表達式可知，仿真信號在0～4 s時間范圍內主要由20、50 Hz兩個標準的正弦信號組成，從2 s時刻開始另疊加一個5 Hz的正弦信號。分別采用傳統的FFT、EMD和EMD-FFT對仿真信號展開分析。

FFT對原始信號在0～4 s時域上的分析如圖1所示。由圖1可以看出:原始波形時域圖上無法準確劃分疊加的5 Hz正弦信號的具體時刻；頻譜圖清晰描繪出仿真信號在0～4s時間存在3種頻率信號，分別為20、50 Hz和5 Hz，但丟失了各頻率成份信號作用的時間信息；FFT計算結果還顯示20 Hz頻率信號對應的幅值為3，50 Hz頻率信號對應的幅值為7，5 Hz頻率信號對應的幅值為0.5，其中50 Hz和20 Hz兩個頻率成分的幅值與仿真信號對應頻率的幅值一致，但是5 Hz頻率成分的幅值卻與實際的不同，出現了衰減，傳統的FFT無法準確提取仿真信號中各頻率成份的幅值。

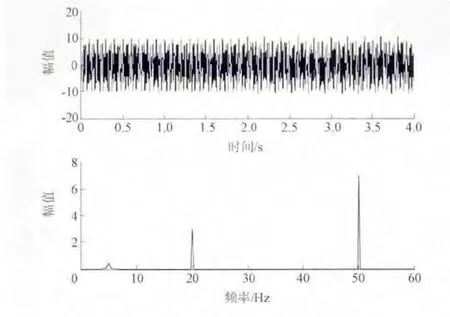
圖1 原始仿真信號時域波形及頻譜

單一FFT分析結果表明，頻譜分析方法僅能獲取信號整體時域的頻譜信息，無法提供各頻率成份作用的時間信息，特別針對非平穩信號，還難以有效提取突變信號成份的幅值信息。

EMD分解建立在信號自身的時間尺度特征上，無需預先設定任何先驗性的基函數，在非平穩信號分析方面具有一定特色，對仿真信號的經驗模態分解產生的各IMF及其頻譜分析如圖2和3所示:EMD按照不同趨勢或尺度，自適應的分解產生一序列IMF，各階IMF分量包含了原仿真信號的不同時間尺度的局部特征信號，隨著分解層數的增加，IMF的頻率越來越低；1IMF和2IMF的波形持續在整個時間段內，1IMF頻率與幅值為50.02 Hz和6.995，2IMF頻率與幅值為20.01Hz和2.888，與仿真信號中的50 Hz和20 Hz信號特征基本一致；3IMF的波形表明該尺度信號僅在虛線圈區域存在，在2 s時刻左右疊加進來的突變信號成份，3IMF頻率及幅值為5.002 Hz和0.463。

EMD分析結果揭示，經驗模態分解可相對準確的劃分各頻率成份信號的發生時刻，捕捉突變信號的時間信息及頻率信息，但所獲取的突變信號的幅值有較大程度衰減，這主要由于EMD分解原理缺乏嚴格正交性制約，導致相近頻率信號分布到不同IMF分量而造成的幅值失真。

FFT能提取待分析時段信號的頻譜信息，僅當該頻率成份為相對穩定信號時，所提取的幅值信息才比較準確，而EMD可將非平穩信號進行平穩化處理，能有效劃分突變信號作用的時間區域。本文所構建的EMD-FFT通過經驗模態分解，劃分突變信號的作用時間，對該時段的原始信號展開FFT分析，獲取該突變成份的時間-頻率-幅值特征。圖4所示的EMD-FFT時頻分析結果表明: 5.005 Hz突變信號作用時間域為2～4 s，幅值為1.004，與仿真信號接近，50 Hz和20 Hz作用于整個0～4 s的幅值也與仿真信號保持一致。

圖2 原始仿真信號EMD分解

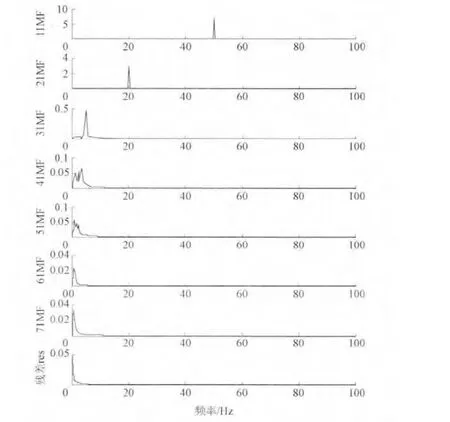
圖3 各階IMF頻譜

圖4 突變信號 （2～4 s）時域波形及頻譜圖

對照FFT、EMD和EMD-FFT分析結果可知，EMD-FFT可作為一種有效的動態信號檢測手段，克服了傳統FFT分析存在丟失時間信息和EMD提取的突變信號幅值衰減的缺陷，能相對精準捕捉突變信號的時間-頻率-幅值特征。

3 EMD-FFT應用于水電機組非平穩信號的征兆提取

下面結合某水電廠機組 （額定轉速為75 r/min，轉頻為1.25 Hz）連續升負荷試驗的下導擺度Y信號，采用EMD-FFT時頻分析，提取突變信號部分的時頻特征。原始信號采樣頻率為1024 Hz，采樣點數據長度為159744點，為了便于計算，這里首先對該信號進行32抽1的重新采樣，則采樣頻率調整為32 Hz，重新采樣后時域波形如圖5。

圖5 下導擺度Y時域波形

由圖5可以看出，水電機組作為涉及水、機、電的大型復雜系統，影響運行因素眾多，連續升負荷過程中的下導擺度Y信號體現出較強的非平穩特征，某負荷區域振動強烈，發生突變。按照EMDFFT時頻分析流程，首先借助EMD經驗模態分解，從各IMF分量時域波形 （如圖6）中，可觀察到突變分量主要集中分布到5IMF和6IMF中，確定突變成份作用時間區域為60～100 s之間，提取該時間區域的Y信號，展開FFT分析，獲取該突變信號成份頻譜特征見表1（僅給出前8位的頻率和幅值）。

圖6 突變信號 （60～100 s）時域波形圖及頻譜

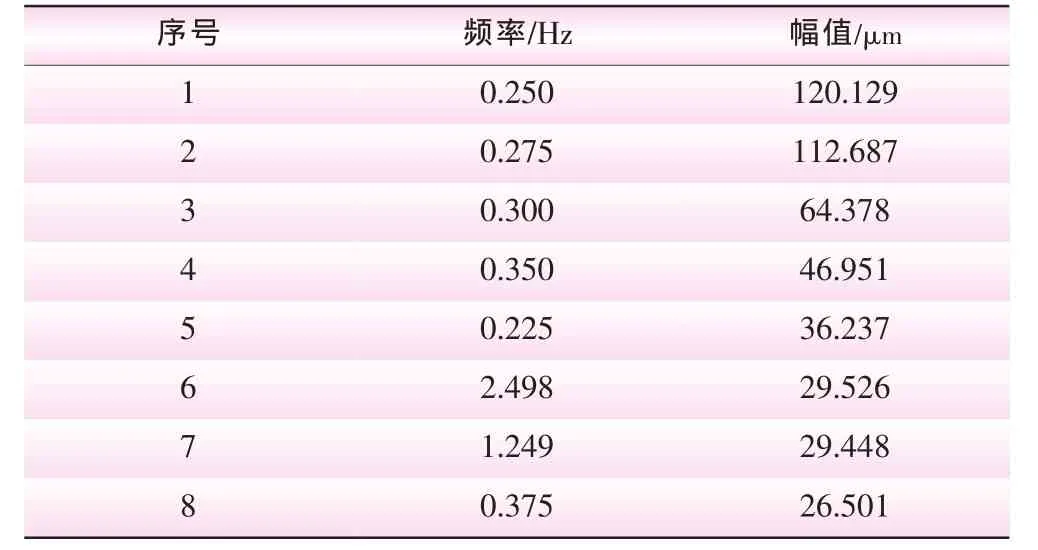
表1 變負荷過程中下導擺度Y突變成份頻譜分析結果

由水輪機工作原理可知，機組在特定負荷區間運行時，尾水管內會形成強制旋渦或旋轉渦帶，引發較強低頻壓力脈動，該脈動頻率一般為1/6～1/2轉頻。EMD-FFT所提取的突變信號發生在60～100s之間，主要頻率為0.25～0.35 Hz之間，機組負荷為388-465 MW，處于渦帶工況，突變信號是由尾水渦帶引起，該方法有效捕捉到變負荷過程中下導擺度Y突變成份的時間-頻率-幅值特征。EMD-FFT提取的突變信號頻率分布在0.25～0.35 Hz之間，原因可能有二:一是FFT分析存在能量泄漏；二是連續變負荷，水力因素造成的低頻振動強度和頻率在時間域上本身就具有一定差異。

4 結 論

針對FFT和EMD在非平穩信號分析時存在一定缺陷，綜合兩者優勢，構建了一種EMD-FFT的信號時頻分析方法。EMD-FFT通過EMD分解，自適應地將非平穩原始信號進行平穩化處理，確定突變成份發生時刻，利用FFT對EMD確定的時段內信號頻譜分析，最終獲得突變信號的時間-頻率-幅值特征。仿真結果表明，EMD-FFT克服了FFT丟失時間信息和EMD幅值衰減的缺陷，為非平穩信號中突變成份的動態檢測提供了一種新手段，并應用到水電機組連續變負荷過程中，成功捕捉了下導擺度Y信號中因尾水渦帶導致低頻突變信號成份的時間-頻率-幅值信息。

［1］王恒超，陳喜陽，何志鋒.基于插值重采樣的信號FFT分析方法研究［J］.水力發電，2012，38（3）:21-23.

［2］張夢禾，陳喜陽，張潤時.三峽左岸6號機組振動分析及量化征兆提取策略［J］.水力發電，2012，38（4）:24-27.

［3］陳喜陽.水電機組穩定性監測中狀態分析方法研究［D］.南京:南京南瑞集團，2008.

［4］朱瑜，王殿，王海洋.基于EMD和信息熵的滾動軸承故障診斷［J］.軸承，2012（6） :50-53.

［5］胡勁松，楊世錫，任達千.一種基于EMD的振動信號時頻分析新方法研究［J］.振動與沖擊，2008，27（8）:71-73，154，178.

［6］司青花，王瀚，何苗，等.EMD譜方法提取水輪機動態特征信息［J］.大電機技術，2011（6） :56-59.

［7］王瀚，羅興锜，薛延剛，等.EMD指標能量提取水輪機尾水管動態特征信息［J］.水力發電學報.2012，31（5）:286-290.

［8］胡愛軍，孫敬敬，向玲.經驗模態分解中的模態混疊問題［J］.振動、測試與診斷，2011，31（4）:429-434，532.