基于布爾集線器的線速多播自路由交換結構

塵福興，李揮，崔凱，張博

（1. 北京大學 深圳研究生院 深圳市云計算關鍵技術和應用重點實驗室，廣東 深圳 518055；2. 國家數字交換系統工程技術研究中心，河南 鄭州 450002）

1 引言

1984年，Huang和Knauer首次對ATM網絡中多播數據的交換問題予以關注，并設計出一種新型交換結構來支持多播，提出了第一個多播交換結構——Starlite[1]。自此，業界對高效的多播結構進行了持續的研究。其中，Saito提出了基于共享存儲式的交換結構來實現多播的方法[2]。但是由于存儲器帶寬的限制使該結構不能夠滿足大規模擴展需求。Yeh提出了一種基于Knockout理論多播交換結構，每個輸入端口采用完全連接的方式連接到輸出接口模塊[3]。Chao提出了基于該結構的多播設計方案，但是由于文獻[3,4]結構的級間采用總線式完全連接方式，所以該結構存在線路器件驅動能力的極限問題，使該類方案在大規模擴展性能上存在瓶頸。

基于 banyan的多播交換結構大多采用多播復制的方法，Lee提出了一種內部無阻塞的復制網絡設計方案[5]，由于該方案累加和網絡及虛擬地址編碼器不適合大規模擴展，會發生滿溢(overflow)的現象；多播地址轉換所需緩存開銷龐大，結構過于復雜，難以滿足大規模擴展的需求。文獻[6]提出了一種能夠為復制網絡提供公平機制的方案，然而它進一步增加了結構復制絡的復雜性，使其難以應用于大規模的交換結構設計中。

文獻[7]提出了一種基于 Clos交換結構多播調度算法，引入了一種路徑分配向量，但整個路徑決策時間復雜度較高，無法大規模擴展。文獻[8]證明了對Clos網絡進行多播路徑匹配是NP完全問題。

基于Crossbar多播交換結構的研究則大都是關于多播調度算法。Hui和Ali分析了在隨機情況下扇出和非扇出交替類的多播調度算法的性能，這些研究都證明了由于信元頭阻塞（HOL blocking）會導致吞吐率大大降低[9,10]。Marsan在理論上證明了對于采用虛擬輸出隊列（VOQ）的大規模多播交換結構，不存在一個有限的提速因子能使許可的多播流量達到100%的吞吐率[11]。Pan提出了一種將信元載荷與目的地址信息分開存儲的方案，但其要求的(N+1)(N為輸入/輸出的端口數)倍于外部鏈路帶寬的加速比，本身就是大規模擴展的瓶頸[12]。

從以上對多播交換結構的研究中可以看出，現有的多播交換結構都無法滿足大規模可擴展、線速多播的要求，本文在分配格理論基礎上，通過將“統計線組”的技術應用到分治網絡中，用合適的集線器來代替該網絡中節點，并從理論上對該結構性能證明，從而得到具有低時延、無抖動和無需排隊緩存優勢以及滿足大規模可擴展以及線速多播需求的線速多播交換結構。該結構在一定條件下能很好地解決多播交換結構大規模可擴展以及線速多播問題的同時，又能保證較好的服務質量。

2 多級互聯完全分布式自路由模型和布爾多播交換單元

2.1 多級互聯分布式自路由模型

多級互連完全分布式自路由模型[13]以分治網絡(divide & conquer)[14]為基礎，而構建的具有高度模塊化，最低的器件復雜度（N lb N）等優點的多播交換結構模型。以N=64[ id:(65):(654):(63)(52)(41): (65): (654): id ]的分治網絡為例，如圖1所示。其中，“:”表示一級2×2單元，而兩級間連線方式用一組位置換群元素表示，如(63)(52)(41)。

圖1 64×64的分治網絡

該類網絡的自路由特性由其“跡trace”和“導guide”[15]序列共同決定，給出了網絡的“跡 trace（TK）”和“導guide(RK)”序列及其自路由過程。對于一個 N×N交換結構，多級互聯網絡（MIN,multi-stage interconnection network）由于其分布式自路由特性，以及其理想的單元復雜度 Θ(NlbN)，因而適用于構造大規模交換結構。交換結構的藝術就是由最基本的2×2元件通過各種拓撲結構以最低的代價構造出符合性能指標的大型交換系統。理想的結構是其規模可以任意遞歸擴展，不存在任何瓶頸。因此基于該分布式自路由模型構建多播交換結構模型的理由和動機是充分的、明顯的。構建多播交換結構的第一步應該分析分布式自路由模型的基本交換單元及其原理。

圖1所示基本單元是由圖2(a)～圖2(c)狀態的自路由排序單元構成，進入該2×2基本自路由排序單元的數據分組排序交換過程可以使用帶內信令來實現，例如，在數據分組的前面加上2位帶內信令。第一位A1表示當前時隙是否有數據分組，1表示存在有效數據分組，0表示不存在有效數據分組即為空分組；當A1為1時第二位D1表示分組的輸出目標端口地址才有意義，否則D1為無效位。故A1D1等于‘10’、‘11’、‘00’、‘01’時分別代表“輸出目標端口為0的有效數據分組”，“輸出目標端口為1的有效數據分組”，“空分組”，“空分組”。

自路由模型的基本2×2單元（如圖2(a)～圖2(c)）按如下規定的線性排序關系實現自路由：10＜00＜11，具體控制方式可參見表1。

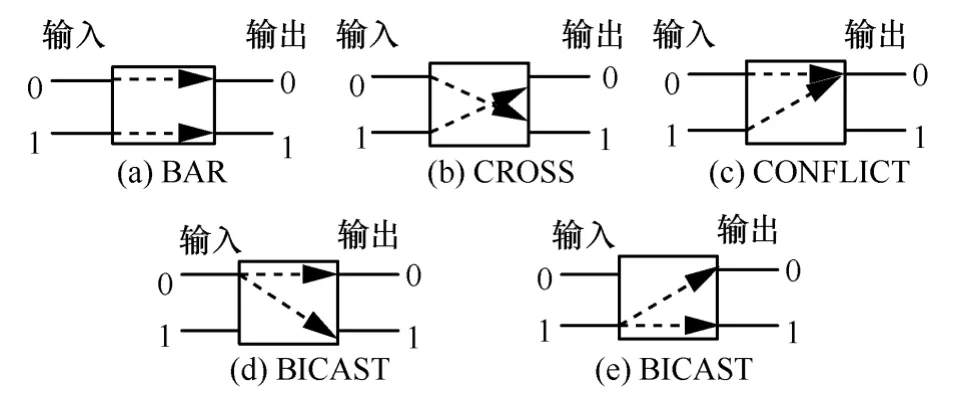
圖2 2×2基本自路由排序單元處于BAR、CROSS、CONFLICT、BICAST的狀態

表1中，CONF(CONFLICT)表示沖突，由其他方式比如優先級來決定哪個信號會被輸出。

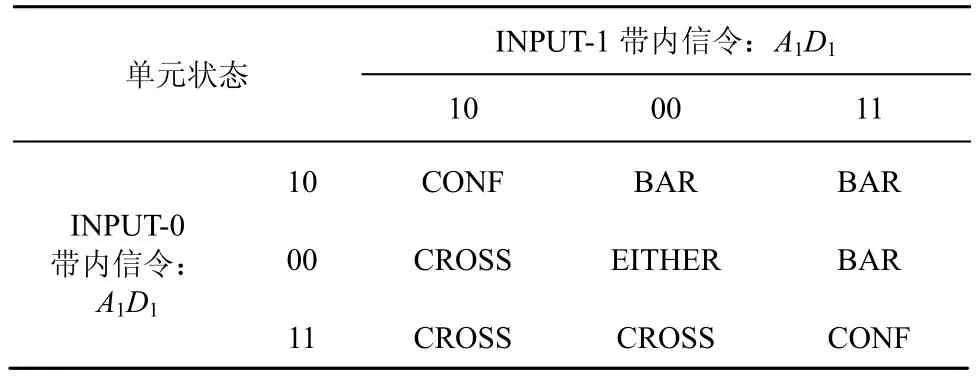
表1 單播2×2基本自路由單元以兩位帶內信令自路由的交換控制

自路由模型的基本單播2×2單元顯然不具備硬件電路拷貝的線速多播特性。為了達到線速多播交換的目的，需要將圖2中只有BAR和CROSS 2種單播路由方式的排序單元進行重新定義，使其成為一種全新的滿足多播要求的排序交換單元，稱為多播交換單元（如圖2(d)、圖2(e)所示）。基本交換單元在加入BICAST狀態后，需要滿足何種條件才能達到線速多播的要求，為了能夠方便描述和證明多播單元以及由其構成的多播網絡特性，本文將從分配格的理論角度來說明。

2.2 布爾多播交換單元

在表1中定義輸入控制的基礎上，可以進一步定義Ωroute={0-bound,1-bound,i dle}，即0?bound=10; 1?bound=11,idle=00。故 10＜00＜11 的線性排序等于如下規則的順序。

規則 1 0?bound＜idle＜1?bound

路由單元按照規則的序列排序即可將盡可能多的有效分組轉發到預定的輸出端口。當出現2個0-bound分組或2個1-bound分組的輸出爭用時，BAR/CROSS狀態的選擇依賴于特定的應用，如信號的優先級。這樣的操作不影響信號自路由的最優性。

當排序單元應用于多播時，必須定義新的帶內信令和相應的交換控制方式，例如表2所示。

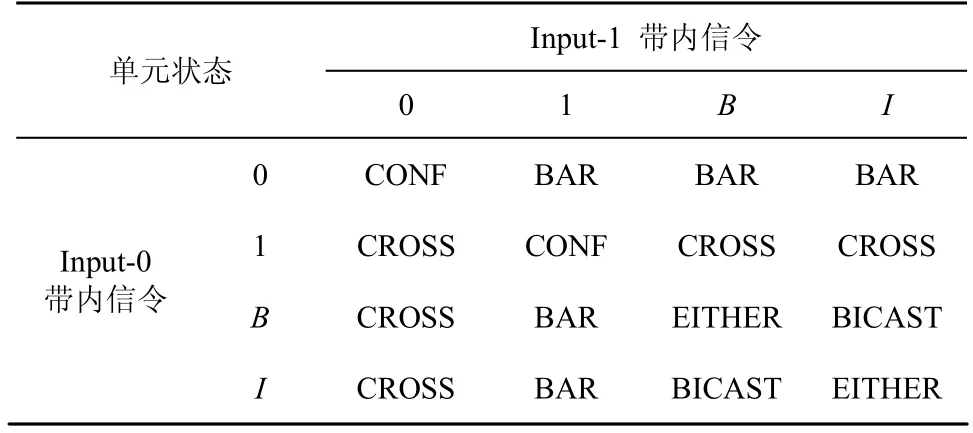
表2 支持多播以線速扇出的2×2多播排序單元的信號控制

表2中，B表示BICAST多播分組（如圖2(d)、圖2(e)所示）；I表示IDLE空分組。

可見支持多播的自路由帶內信令控制表必須擴展為?bicast=?route∪{bicast}。

這個擴展集合由規則1和規則2各自部分排序得到。多播單元對屬于集合?bicast的信號執行排序，當idle遇到bicast時交換控制遵循規則3。

規則 2 0?bound＜bicast＜1?bound

規則3 output-0端口輸出信號值0-bound，output-1端口輸出信號值1-bound，其后都跟隨著相同的負載。

這樣，分組的負載在通過多播單元時可以是BAR狀態、CROSS狀態或者BICAST狀態的硬件電路拷貝的線速多播方式。按這種方式，多播單元能將盡可能多的分組負載轉發到其預定目標端口。

為了能夠方便分析多播單元的特性，排序規則1、2與交換規則3需要尋求一種可以同時滿足3種排序規則的理論，而分配格理論剛好能夠滿足需求。格是一個有二元操作數布爾和∨與布爾積∧，且遵守布爾交換律、布爾結合律、布爾冪等律、布爾吸收率的集合[15]。

常見的格是遵守布爾操作中并集和交集運算的集合的一組子集。

規則4 a≤b?a∧b=a

根據規則4，每一個格都可以導出一個部分有序序列。如果一個部分有序集合（簡稱偏序集）中任意兩元素存在一個最大下界和一個最小上界，則稱這個偏序集為偏序格，用布爾和與布爾積表示這2個界限，偏序格邏輯上等同于格。圖3所示為2種格的舉例，其中圖3(a)是有3個變量的自由格，圖3(b)為分配格。

根據規則1和規則2，圖3(b)描述了?bicast的部分排序，很明顯偏序集?bicast具有偏序格的特性，因此被稱為格。至此多播單元運行的3個規則1到規則3能夠被統一于以下布爾規則（規則5）。

規則5 輸出端口0的值為2個輸入的布爾積，輸出端口1的值為2個輸入的布爾和。

如果一個格滿足分配律

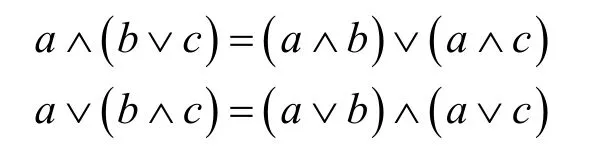
則此格為分配格。?bicast就是一個簡單的例子，如圖 3(b)所示。因此有時也把該多播單元稱為布爾單元。

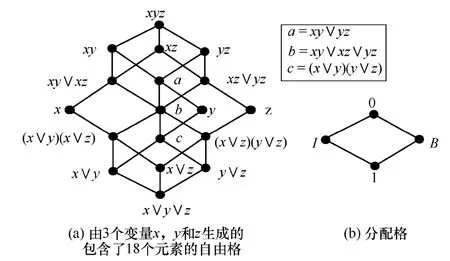
圖3 2種格的舉例

本研究采用分配格來構建多播排序和多播交換的自路由帶內信號表。到目前為止，常用交換結構信號表使用的都是線性有序集，尤其當信號值為數字表示的時候更是如此。對所有帶內信號進行完全排序的要求不僅限制了結構的應用范圍，而且完全阻礙了多播操作。把2×2多播單元與2×2單播單元從分配格的角度來對比可以清楚地看出這一點。

2.3 多播集線器到布爾多播集線器一般化

定理1 （多播集線器定理[16]）以排序單元多級互聯網絡構建的n-to-m的集線器（n個輸入，m個輸出的集線器）為參考，將其中的排序單元用多播單元替換。記信號表為?bicast，不妨設，輸入 V0個 0-bound，V1個 1-bound，以及VB個多播信號。可得到以下結論。

結論1 上面n?m個輸出端口最大可能產生共min｛n-m,V0+VB｝個0-bound和多播信號。

結論2 下面 m個輸出端口最大可能產生共min｛m,V1+VB｝個1-bound和多播信號。

2.2 節把基本交換排序單元統一到布爾單元并用布爾代數來描述，此處由基本單元多級互聯構成的多播集線器同樣用布爾代數來描述。

定義1 令Vj(0≤j≤n)為n個變量 X0,X1,…,X(n-1)的合取范式。若1≤m＜n，當

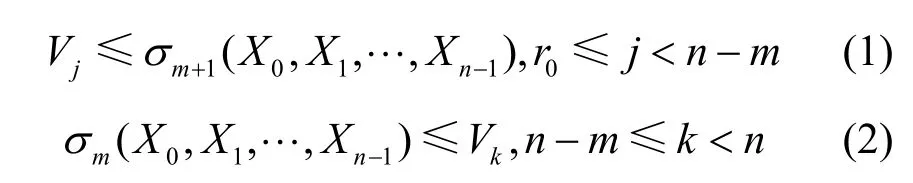
成立時，相應的布爾交換器被稱為是n-to-m布爾集線器。

n×n布爾排序器在一定條件下等同于布爾集線器。如2×2布爾排序器和2-to-1布爾集線器，其實和布爾單元一樣。

推論1 當Vj和σk應用在任意分配格中的n元素而不是變量 X0,X1,…,X(n-1)的時候，式(1)、式(2)在定義1中仍是正確的。

在推論1中分配格的假設是關鍵，因為分配率的應用在合取范式中的作用是非常重要。當一個有序集合是分配格時，布爾集線器相對于普通集線器是一個高級版本。

定理2 （布爾集線器的0-1原理[16]）當且僅當輸入任意包含n?m個0和m個1的序列后，上面的n?m個端口輸出值為0，下面m個端口輸出值為1時，n×n布爾交換器就是n-to-m布爾集線器。

3 大規模擴展線速多播交換結構模型

為了構建大規模擴展多播交換結構模型，本文把“統計線組”[15]技術應用到2.1節的分治網絡中。將自路由分治網絡中的每一個2×2節點放大為2G×2G節點，并用 2G-to-G布爾多播集線器替換該節點，交換網絡中每一根連接線用一束共G根線替換，從而構造了一個帶有統計復用特點的多播自路由結構，每G根輸出線共享一個群組地址。由于通信波動和突發性引發的分組丟失率隨 G值的增大呈指數級減小[13]，在可允許的輸入流量下，“統計線組”技術可以達到幾乎無阻塞交換。

在實際應用中G表示為群組，將G根線組成的一束記為一個群組，這個值一般比較大，K表示群組數，N表示交換結構的輸入/輸出的總線數N=KG。

如圖 4(a)所示為一個 N=128，K=16，G=8的多播路由交換結構。該結構是通過將 16×16的banyan網絡中每一個2×2節點替換為2G-to-G的由布爾單元組成的布爾集線器來實現。這里G=8，在實際應用中G本應該為一個大的數，所以一個2n×2n banyan-type的G-line版本的網絡構建成了一個 N×N的幾乎無阻塞的多播交換器。根據 fast knockout[17]集線器構造算法或利用 bitonic circular再配合一級半清器（half-cleaner）[15]，可構造G為任意大小的群組集線器，從而保證了交換結構的大規模可擴展性能。

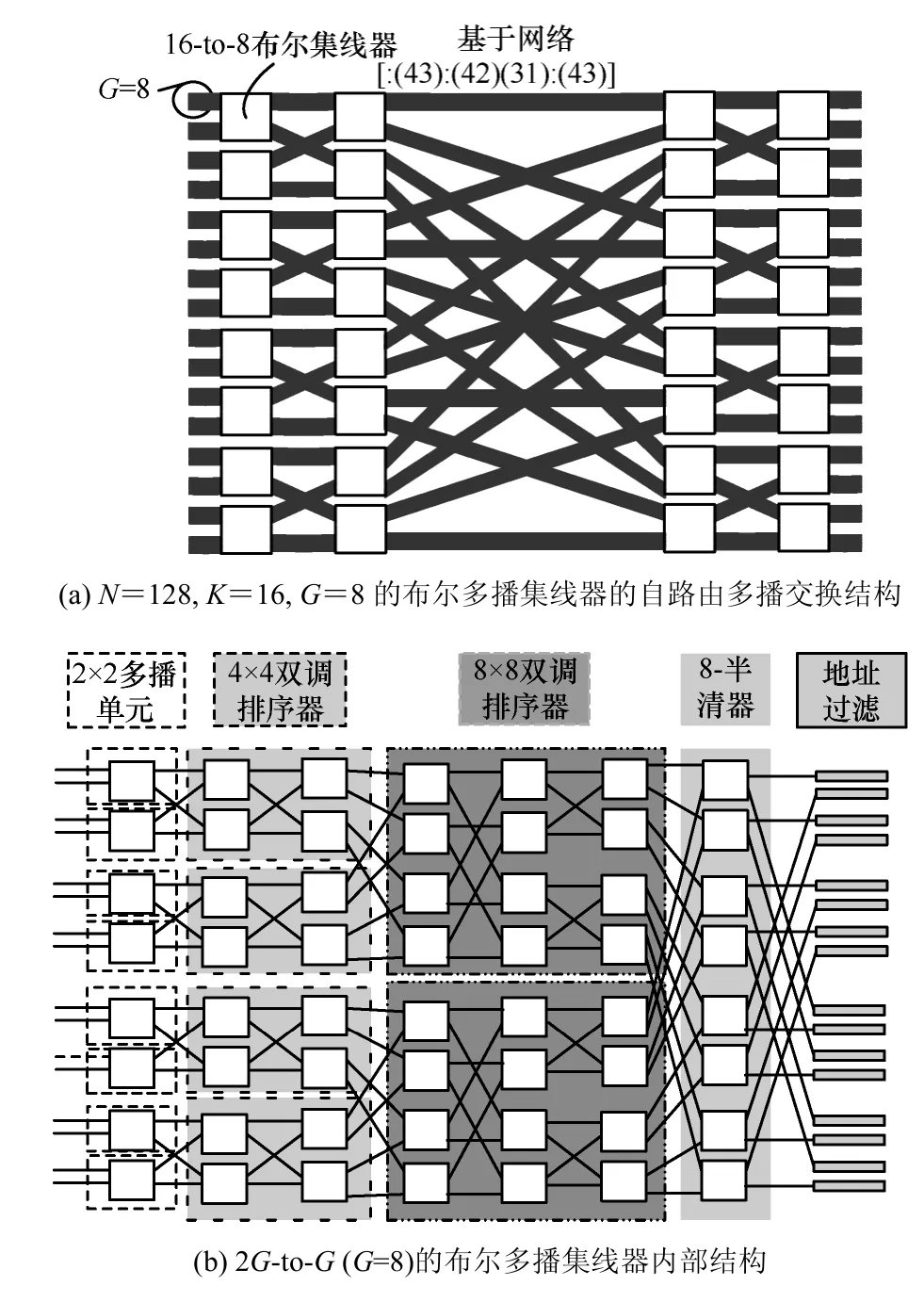
圖4 布爾多播集線器交換結構及內部結構

圖4(b)所示為圖4(a)中任一個2G-to-G的布爾多播集線器的內部結構圖。圖4(b)中的每一級（除了最后一級地址過濾器）中最小的單元即為2.2節的布爾多播交換單元。由圖4可以對本文提出線速多播交換的內部結構有一個更詳細的理解。

本文提出的線速多播交換模型所采用的完全自路由分治網絡結構和布爾多播集線器都具有良好的大規模可擴展性，交換結構中每個最小的交換單元使用硬件電路拷貝的方式實現多播，從而保證了交換結構的線速多播以及大規模可擴展特性。此外，交換結構模型中無排隊緩存，更不需要調度從而保證了多播時延不會高于某一個定值。

對于定理1，當有一個適當的多播信號表?bicast為輸入時，多播集線器就能夠達到最優的多播交換。而多播交換網絡則是由多播集線器遞歸構造而成，當用布爾單元代替集線器網絡中的排序單元時，對任意的一個格或分配格結構的信號表，該定理是否也成立。由此深入考慮?bicast格結構的支持多播集線器定理的本質屬性，仔細觀察發現?bicast在結論1中分為上部理想{0,B}和下部理想{1,1}，在結論2中類似地分為{1,B}和{0,1}。

定理3 如果格 ?的非空子集 S滿足條件x∈S,y∈S?x∧y∈S,x∨y∈S，則S為子格；如果x∈S,y∈S?x∧y∈S，則子格S是一個上部理想；如果x∈S,y∈S?x∨y∈S，則子格S是一個下部理想。

定義2 如果2個格之間映射保持布爾運算不變，則稱該映射為格同態。

如從格?到?2的格同態等同于格?劃分為一個上部理想和一個下部理想。

定理4 設μ是格?映射到?2的一個同態，那么格?上部理想為μ-1(0)和下部理想為μ-1(1)。若將格 ?劃分為上部理想 U和下部理想 L，對s∈U ,μ(s)=0和s∈L,μ(s)=1，則可以得到μ是格?到?2的同態。

定理5 對于由排序單元多級互聯網絡構成的n-to-m集線器，用布爾單元替換多級互聯網絡中所有的排序單元，所得到一個n-to-m布爾集線器網絡便稱之為布爾集線器。

將任意的分配格?劃分為上部理想U和下部理想L。從U中輸入u個值，0≤u≤m，從L中n-u個值進入集線器網絡之后，有如下結論。

結論3 上部n?m個端口輸出min{n-m,u}屬于U的值。

結論4 下部m個端口輸出min{m,n-u}屬于L的值。

證明 根據定理5可知上述的單元為一個n-to-m布爾集線器。為了證明定理剩下的部分，令μ表示和s∈L,μ(s)=1中?到?2的同態。

用μ(s)替換每一個輸入信號 s。這就將 n個輸入信號值轉變為u個0的和n?u個1的組合。從集線器網絡的性質可知，上部n?m端口輸出為min{n-m,u}個0和下部n端口輸出個1。因為μ是一個格同態，級間用同樣的信號替代。當替代后集線器的一個輸出端口輸出值0或1時，則替代前其輸出值分別屬于μ-1(0)=U 或μ-1(1)=L。證畢。

將定理5應用到Ω=Ωbicast，U={0,B}，L={I,1}，那么結論1和結論3變為完全相同。類似地，U={0,1}和L={B,1}結論2將和結論4一致。

定理6 針對大規模可擴展多播結構中的n-to-m集線器，將所有的排序單元用bicast單元來替換，則當信號表是?bicast時，以下結論中有一項成立。

結論5 上面的n?m個端口輸出僅為0-bound信號。

結論6 下面的 m個端口輸出僅為1-bound信號。

結論7 沒有端口輸出為idle信號。結論8 沒有端口輸出為bicast信號。

證明 信號值 0-bound，1-bound，bicast和idle分別為0，1，B和I。bicast單元組成的多級互聯網絡的精確輸入組合為：V0個 0，V1個 1，VB個B，VI個I。由圖3(b)可看到該信號表滿足分配格的結構，若將多級互聯網絡中的 bicast單元用布爾單元替換，則布爾集線器定理得以應用，同時也保證了布爾集線器網絡構成及式(1)、式(2)的應用。證畢。

將信號表?bicast表示的格劃分為上部理想U={0,B}和下部理想L={I,1}。可以得到由n元組構成的對稱多項式σm+1的如下性質。

性質1 如果 V1+VI≥m+ 1，可得 σm+1的值不是1就是I，因為σm+1中的一些單項式只與n個變量中賦值為1和B的值的變量有關。

性質2 如果 V1+VI≤m+ 1，可得 σm+1的值不是0就是B，因為σm+1中的一些單項式只與n個變量中賦值為0或B的值的變量有關。

另一種是，將理想的分為上部分U={1,B}和下部分L={0,I}。同理可得以下性質結論。

性質3 如果 V1+VB≥m+ 1，可得 σm+1的值是1或B。

性質4 如果 V1+VB≤m + 1，可得 σm+1的值是0 或 I。

假設性質2和性質4成立，σm+1唯一可能的值就是0，再由式(1)可以得出結論4成立。

對稱地，假設性質1和性質3成立，σm+1唯一可能的值就是1，因此σm=1，再由式(2)可以得出結論6成立。

假設性質2和性質3成立，σm+1唯一可能的值就是B，因此σm≥σm+1=B。從式(1)可以得出，上部分n?m 個端口輸出不可能為I。從式(2)可以得出，下部分m個端口輸出也不可能為I。所以結論7可以成立。

由對稱的特性可得，在性質1、性質4假設下結論8也成立。

在定理6中，0-bound和bicast信號總數在多級互聯網絡被逐級保留，1-bound和 bicast信號總數亦然。同樣可以看出結論5到結論8的每一個聲明都暗示著結論1和結論2成立。因此定理6應該可以說是布爾多播集線器原理的一個詳細版本。從定理6可以得出一個更通用的結論：布爾集線器理論不僅僅可以把盡可能多的信號路由到目的輸出群組，而且可以依據“優先級”的不同而達到最佳路由。此處的“優先級”要求集線器的信號表必須是分配格。這個定理適合通過各種可能的方式去劃分分配格的上部理想和下部理想。通過以下例子來說明。

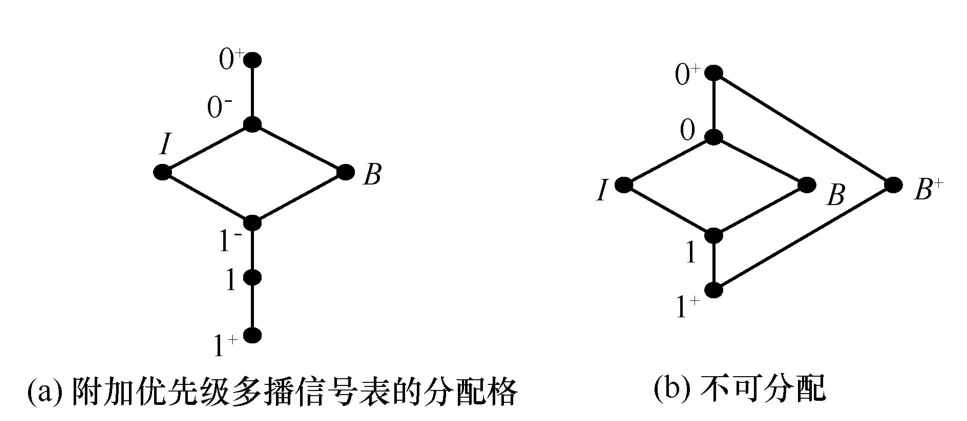
圖5 優先級多播信號表示例

設Ω={0+,0-,I,B,1-,1,1+}為在圖 5(a)中的分配格。?中元素的命名規則為：上標‘+’為到達期望集線器的目的地址0或1的最高優先級，‘?’表示最低優先級。?中所有通過一個n-to-m布爾集線器的路由信號的優先級涉及了所有可能的對 ?的劃分為上部理想U集合和下部的理想L集合。這里可以組合

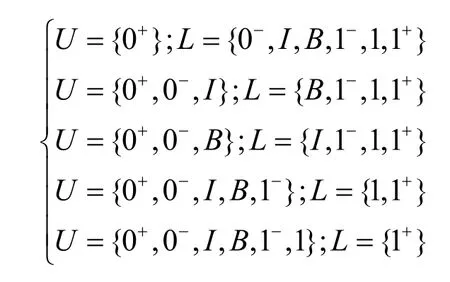
從定理5可以看出，在去往輸出群組0的元素中集合U中的每一個元素都比集合L中的元素的優先級要高；同樣，信號路由到輸出群組1也是如此。應用這個理論到上面所列出的5個劃分方法可以得到以下結論。

結論9 在有序子集{0+,0-,B,1-,1,1+}的信號中去往輸出群組 0的較小的元素被賦予較高優先級，然而去往輸出群組1的信號被賦予較高的優先級。布爾集線器的路由最佳性是和這個優先級的策略相一致的。

結論10 類似的優先級處理同樣可以應用在有序子集{0+,0-,I ,1-,1,1+}中。

結論11 同時，B和I這2個信號在路由向任意輸出群組時被賦予同樣的優先級，這就意味著B和I不能同時出現在彼此對立的輸出群組中。

如圖6(a)實例說明分配格?的信號通過一個8-to-4布爾集線器網絡的傳播過程，其中有上標‘+’的信號是具有高優先權處理的。0，1，B，I分別表示 0-bound，1-bound，bicast和 idle。圖中陰影部分單元表示發生多播的信號，在這里bicast和idle信號被0-bound和1-bound信號所替換。這樣輸出群組0得到盡可能多的0-bound和bicast信號，同時輸出群組 1得到盡可能的1-bound和bicast信號。此外，這個路由最優是和結論9和結論11相一致的。

例如，圖6(b)例證了圖5(b)中非分配格Ω={0+,0-,I,B,1-,1,1+}中信號值通過同一個8-to-3布爾集線網絡的傳播過程，其理想的交換是得不到保障的。因為在這個格中 B+∧I=0+和B+∨I=1+，一個高優先級的bicast信號在一個布爾單元中遇到一個idle信號后輸出高優先級0-bound和1-bound信號，從而導致輸出群組0丟失了一個有效信號，同時也只有一個有效信號出現在輸出群組0。這個次優的路由結果反應了在定義布爾交換，集線器或排序器中輸入信號需要滿足分配格的結構才能達到最優的多播交換。

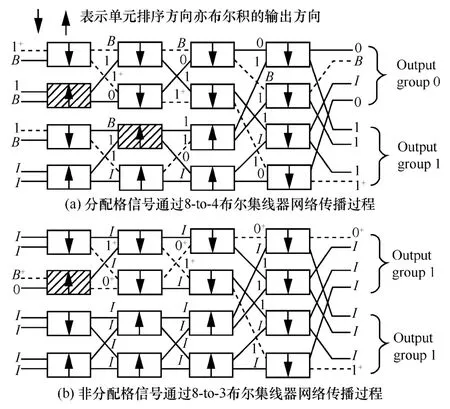
圖6 信號通過布爾集線器網絡傳播過程

在實際應用中非分配格有時會被用作信號表，因為高優先級多播通信在整個通信量中占很小一部分，那么布爾集線器理論依舊能夠被統計應用，這是一個特殊情況。

4 線速多播結構阻塞率模型分析

從上述布爾多播單元 bicast的狀態可以看出，該多播交換結構的特點是在交換網絡中線速扇出。當扇出為1時即是單播，否則就是多播，所以該交換多播交換結構支持單多播的混合輸入。分組的扇出率（多播扇出的個數）直接影響了其阻塞率。由于交換的規模是由其級數決定的，交換規模越大，多播分組扇出的可能性也就越大，交換的級數對阻塞率和扇出率也有直接的影響。

單播時自路由路徑 trace(guide)[15]信息表示為dφ(g)… dφ(2)dφ(1)1，其中，下角標φ (1),φ(2),…,φ(g)表示級間置換信息[13]。多播分組頭信息序列為…Q110Q010Q100Q000Q01Q10Q00Q1Q01，多播分組頭信息的第一位1為多播有效位，此分組序列包含了該多播中所有單播的信息，從右向左依次排序，可以分解為多個單播分組的信息頭，并且都滿足單播的級間置換規則。

不妨設第 i(1≤i≤m)級布爾集線器內單播分組控制信令為dφ(i)，多播分組控制信令為Qqi1，qi是二進制數，其長度為i?1。每當空分組I與多播分組B在同一個2×2的布爾單元相遇時，若該級滿足多播扇出控制要求，其兩端口的輸出控制信息則采用cut-through[15]的方法將多播信息頭進行分割，否則多播頭信息不發生變化。

下面具體分析線速多播交換結構在不同網絡負載下的分組阻塞率情況。假定各輸入群組所到達的分組滿足獨立同分布的要求，在某一時隙到達交換結構網絡中第i級2G-to-G布爾集線器中某交換單元某輸入/輸出群組的分組數目表示為XIi/XOi(1≤i≤m )，其中，0≤XIi≤G,0≤XOi≤G 。

設交換結構到達的業務數據總額為1，單播業務所占比例參數λ=P1，表示在單個時隙內單播業務到達的概率為P1，多播業務所占比例參數為λ=P2，表示單個時隙里多播業務到達的概率 P2，用XI1s表示進入交換結構的第一級中某輸入群組的單播分組個數，則

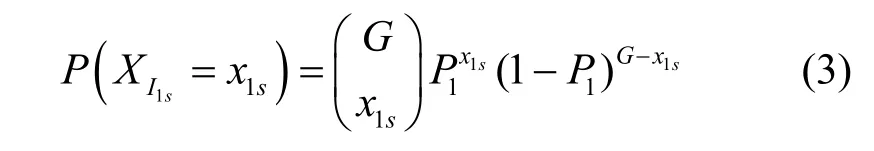
其中，XI1m表示進入交換結構的第一級某輸入群組的多播分組個數。

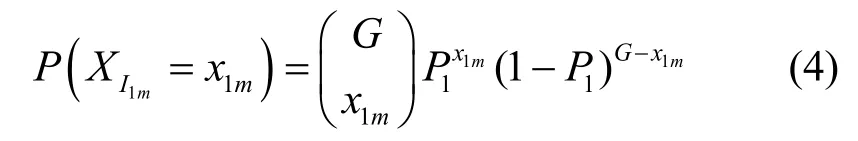
P=P1+P2,x1=xs+xm，其中，xs表示單播分組個數，xm表示多播分組個數。如果xm≠0，表示存在多播分組，由于多播分組扇出的特點，那么在交換結構中的某集線器最后輸出的分組個數在一定概率上要比輸入的分組多一些。假設每個多播分組在交換結構的每一級都要求發生多播，即其帶內多播控制信號全是由2k-1個B構成，由于布爾集線器的輸入信號表為嚴格的分配格結構，即當單播與多播在集線器內爭用同一個出口時，根據交換規則單播優先級高而占用輸出端口，導致其多播會被誤路由，所以該多播只能以一定的概率扇出。XI1，YI1為交換結構中第一級集線器的輸入，滿足獨立同分布要求。用AI1表示第一級布爾集線器輸入分組的總和。為了簡化表達式用DI(di)表示 DI=di時的概率P(DI=di)。

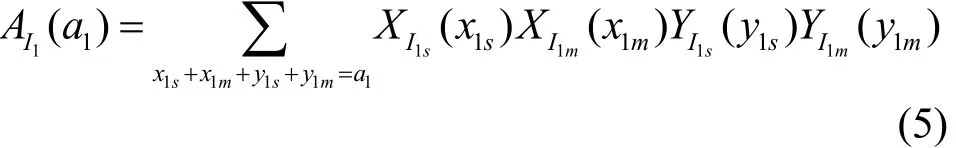
?a1≤2G,?I∧B=0,I∨B=1，使a1+x1m2+y1m2≤2G，其中，x1m=x1m1+x1m2，y1m=y1m1+y1m2，x1m1，y1m1為扇出為1的多播分組（即為單播分組），x1m2，y1m2為扇出2的多播分組。從而可得實際的輸出分組總和

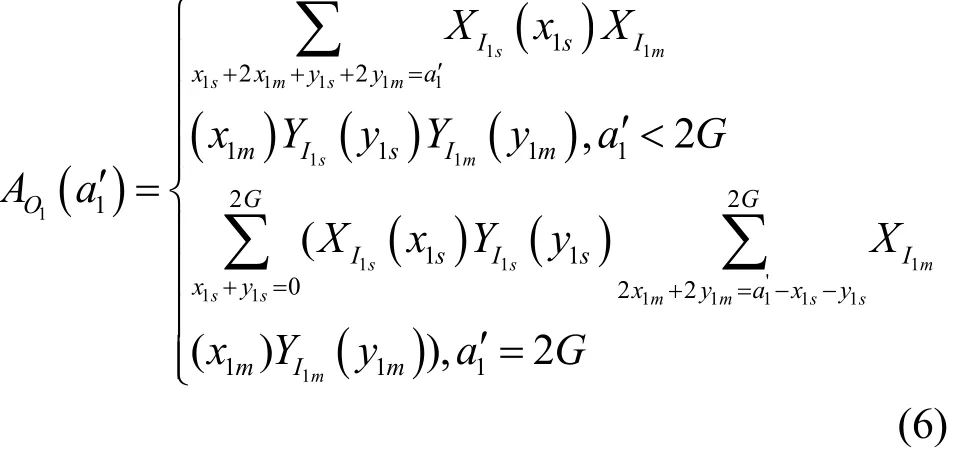
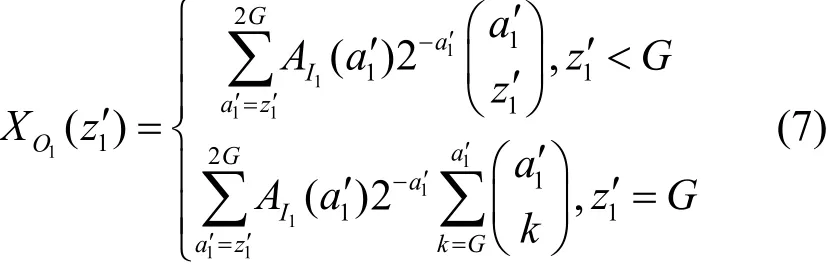
其中，λ1m=1-λ1s，λ1m=1-，已知多播交換結構的第i級集線器的輸出是第i+1級集線器的輸入，即滿足相同分布，由此可得集線器實際輸入的分組總數ai+1服從以下分布。

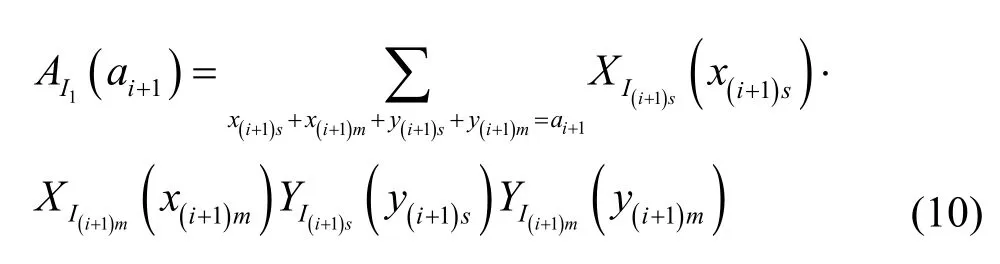
集線器實際輸出的分組總數ai′+1服從以下分布。

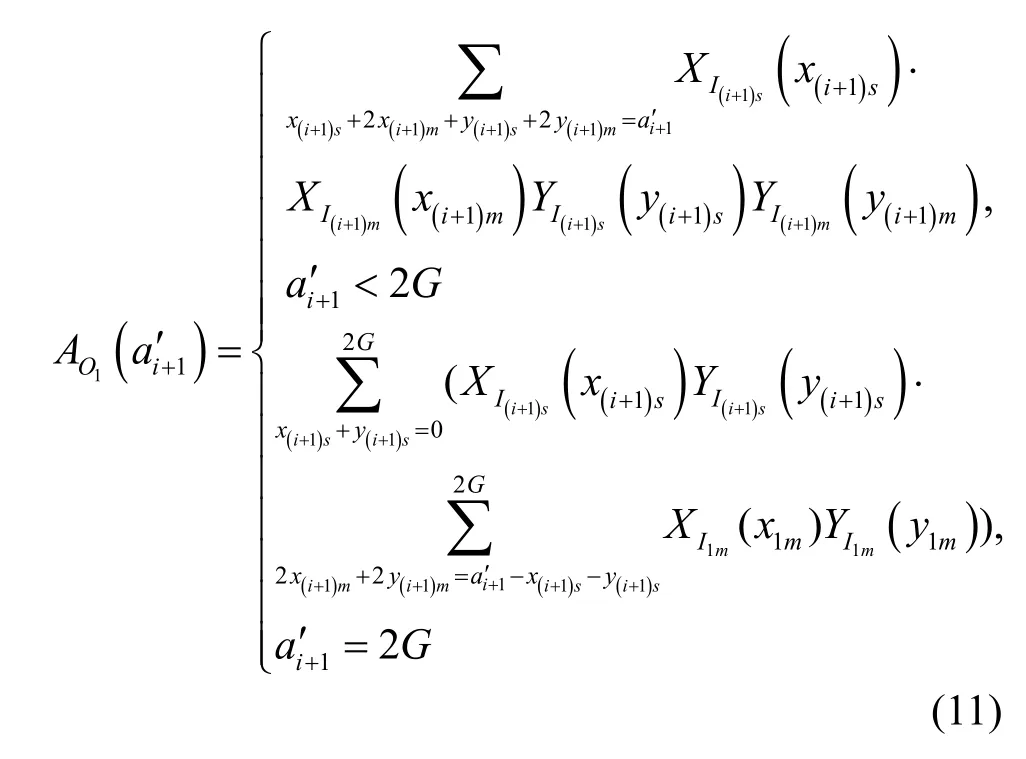
同樣可得出第i+1級布爾集線器的某輸出群組單多播分組總數的分布：

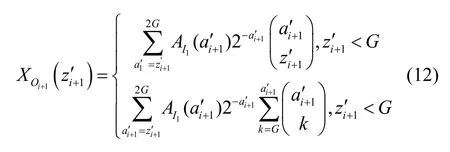
重復上述步驟可以推導出第i+1級布爾集線器輸出的單播分組個數XO(i+1)s分布，以及多播分組個數XO(i+1)m分布。通過的迭代的方法，可得第k級布爾集線器某輸出群組單多播分組個數的分布情況 XOks，XOkm。

單播阻塞率指平均輸入單播分組減去輸出單播分組數的平均值后再與平均輸入單播分組數的比，得式(13)。

多播的阻塞率要考慮扇出的因素，多播的輸出分組會遠大于輸入分組，所以多播的阻塞率應該為平均輸出多播分組數與理想最大輸出多播分組數的比，得式(14)。其中，(k+1)Gp2mod(G-Gp1)的含義為：因帶內控制信令由全B組成，所以理想最大可扇出分組數可表示為(k+1)Gp2，但受到輸出端口數G的限制和單播輸入分組數Gp1的與多播分組爭用端口的影響，最大可輸出多播分組數表示為(k+1)Gp2mod(G-Gp1)。

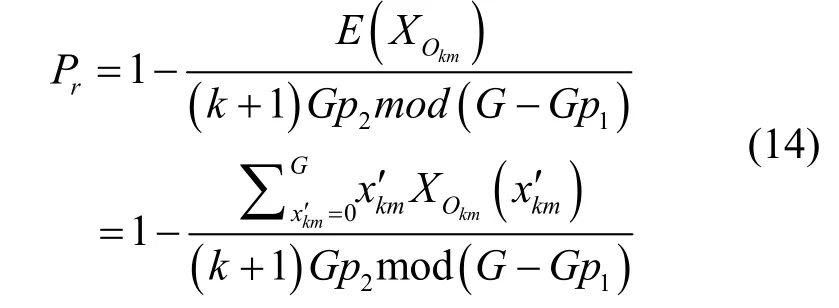
5 仿真結果

本節采用C++編程實現在均勻分布業務源下對線速多播交換結構的多播阻塞率和時延的仿真。阻塞率是指分組在經過交換系統時沒能被成功交換到目的端口的概率。時延是指分組第一個比特進入交換系統到分組第一個比特從交換系統輸出時所需要的時間。時延在交換系統中一般分為傳播時延和信號處理時延。仿真過程要求數據源滿足伯努利均勻分布，集線器的群組輸入業務要求服從二項分布，到達的業務強度用歸一化負載表示。

1)多播阻塞率仿真

負載強度對阻塞率有直接的影響，本節選取一個一個代表性的負載，不妨設單播業務所占負載的比例為P1=0.2，則可得多播業務所占負載的比例為0≤P2≤1-P1。在多播業務強度相對固定的情況下，通過改變交換網絡的級數參數K以及群組參數G的大小仿真多播阻塞率的情況。選取在K=4的條件下仿真并比較 G=8,16,32時多播的阻塞率情況。從圖7可以看出，隨著G增大其阻塞率而減小。因為參數K決定了交換結構網絡的級數，當K不變且單播業務負載強度相同時，則單播與多播在集線器中發生爭用的情況基本相同。然而若G變大，分組在布爾集線器內部發生爭用的概率就變小，阻塞率也就越小。

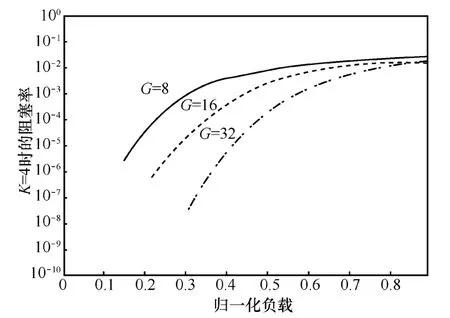
圖7 G不同時的多播阻塞率

圖8的顯示的是群組G=32時，K=4、8、16時得到的多播阻塞率仿真結果。從圖中曲線可看出K變大其阻塞率也變大，然而在同一負載點上，K的不同，其阻塞率區別不明顯。這是因為由于多播的扇出特性，當交換結構網絡級數不小于 4，歸一化負載P2≥0.2時，得到扇出的多播分組數接近G-0.2G=0.8G所以在最后的幾級布爾多播集線器中多播分組被扇出的概率會很小，所以在G=32歸一化負載下，雖然k不同，但其阻塞率差別并不明顯。

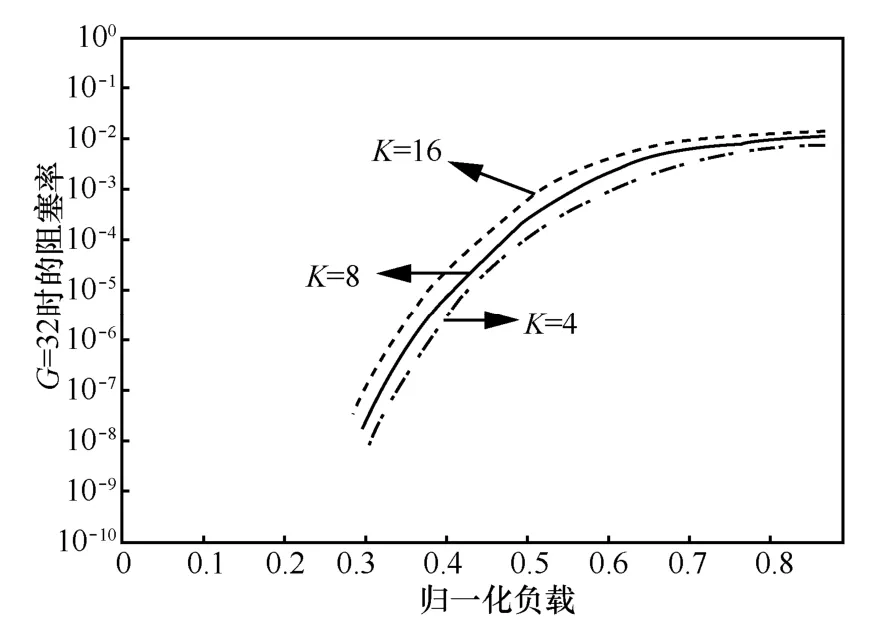
圖8 K不同時的多播阻塞率

2)多播分組時延仿真

多播分組在經過交換結構網絡的每一個布爾集線器中的每一個2×2布爾單元時，需要一定的時間完成對分組數據的處理，從而產生了時延。所以多播分組的時延主要由分組所經過基本布爾單元個數決定，設分組在經過任一個布爾單元時對數據處理的時間即時延為Δd。

多播交換結構網絡的規模由k決定，每一個布爾集線器的規模則是G決定，交換結構中布爾單元的個數則是由K和G共同決定。為了仿真多播時延數據，不妨先固定一個參數，設K=4，可以得到G=8,16,32的時延，如圖9所示。

從圖9中可看出G越小時延也越小。從圖中還可以看出 G不同時，各時延增長速度Tv的關系為Tv(G=32)＜Tv(G=16)＜Tv(G=8)，這是因為G=32的阻塞率是最小的，所以分組丟失的概率較小，統計分組時延也就會最低。隨著負載的增大，當負載大于 0.6時，時延增加的速度加快。

固定參數G=32時，得到K=4、8、12的時延仿真結果，如圖10所示，K越小其時延越小，K不同。從圖8可以得知，K不同，其阻塞率的變化不明顯，所以該時延曲線的變化也不明顯。該多播交換結構采用的多級互聯的結構，無論G，K參數如何變化，其時延也總會小于某一個定值。

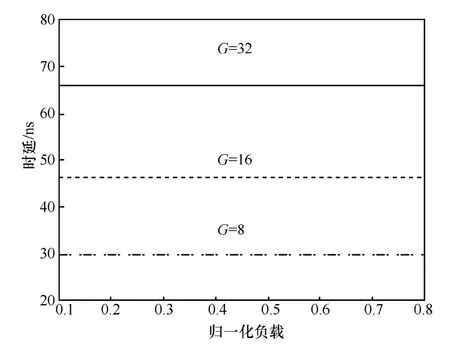
圖9 K=4，G不同時的多播時延

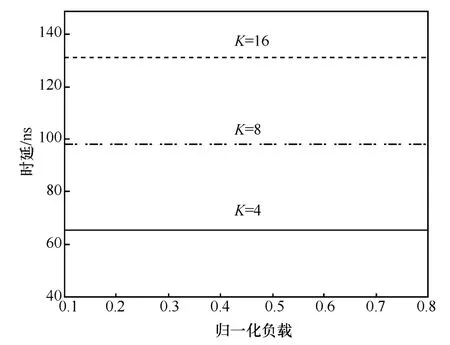
圖10 G=32，K不同時的多播時延

6 結束語

本文提出的基于分配格的線速多播交換模型，具有低時延、無抖動、可大規模擴展優點，當多播業務負載強度控制在一定可允許的范圍內時，其多播業務的阻塞率可以被接受，其多播時延總會小于某個定值，且該定值會在百納秒量級，所以該交換結構能夠為到達業務提供時延上限保障。該交換結構模型可以解決某些網絡環境中對業務的特殊需求應用的問題，如時延、阻塞率、線速多播等。

[1]HUANG A. Starlite: a wideband digital switch[A]. Proc Globecom'84[C]. Atlanta,GA,1984.1-5.

[2]SAITO H,YAMANAKA H,YAMADA H,et al. Multicast function and its LSI implementation in a shared multibuffer ATM switch[A].Networking for Global Communications,13th Proceedings IEEE[C].Toronto,Ont,1994.315-322.

[3]YEH Y S,HLUCHYJ M,ACAMPORA A. The knockout switch: a simple,modular architecture for high-performance packet switching[J].Selected Areas in Communications,1987,5(8):1274-1283.

[4]CHAO H J,CHOE B S,PARK J S,et al. Design and implementation of abacus switch: a scalable multicast ATM switch[J]. Selected Areas in Communications,1997,15(5):830-843.

[5]LEE T T. Nonblocking copy networks for multicast packet switching[J]. Selected Areas in Communications,1988,6(9): 1455-1467.

[6]CHAO H J,LIU B. High performance switches and routers[M].Wiley-IEEE Press,2007.

[7]MARCHOK D J,ROHRS C E,SCHAFER R M. Multicasting in a growable packet (ATM)switch[A]. INFOCOM'91. Proceedings. Tenth Annual Joint Conference of the IEEE Computer and Communications Societies Networking [C]. BalHarbour,FL,1991. 850-858.

[8]JASTRZEBSKI A,KUBALE M. Rearrangeability in multicast clos networks is np-complete[A]. Information Technology(ICJT)[C]. Gdansk,2010,183-186.

[9]HUI J Y,RENNER T.Queueing analysis for multicast packet switching[J]. IEEE Transaction Communications,1994,42(234): 723-731.

[10]ALI MK M,YANG S. Performance analysis of a random packet selection policy for multicast switching[J]. IEEE Transactions Communications,1996,44(3):388-398.

[11]MARSAN M A,BIANCO A,GIACCONE P,et al. Multicast traffic in input-queued switches: optimal scheduling and maximum throughput[J]. IEEE/ACM Transactions on Networking (TON),2003,11(3):465-477.

[12]PAN D,YANG Y. FIFO-based multicast scheduling algorithm for virtual output queued packet switches[J]. Computers,IEEE Transactions,2005,54(10):1283-1297.

[13]HE W,LI H,WANG B,et al. Load-balanced multipath self-routing switching structure by concentrators[A]. IEEE International Conference on Communications,ICC’08[C]. Beijing,China,2008.5935-5939.

[14]LI H,LI S Y R. Layout complexity of bit-permuting exchange in multi-stage interconnection networks[M]. Boston: Kluwer Academic Publishers,2001.259-276.

[15]LI S Y R. Algebraic switching theory and broadband applications[M].Academic Press,2001.

[16]LI S Y R. Unified algebraic theory of sorting,routing,multicasting,and concentration networks[J]. IEEE Transactions Communications,2010,58(1):247-256.

[17]LI S Y R,LI H,KOO G M. Fast knockout algorithm for self-route concentration[J]. Computer Communications,1999,22(17):1574-1584.

[18]LI H,LI S Y R. On the Complexity of Concentrators and Multi-stage Interconnection Networks in Switching System[D]. Hong Kong: Chinese University of Hong Kong,2011.