講究策略 學好三角函數

黃友波

（福建省寧德市第五中學，福建 寧德 352100）

三角函數是高中數學新課程中的重要內容，在這些內容中強調了三角函數作為函數的作用，強調了三角函數是刻畫周期現象的基本模型等，這是數學課程發展中的一個變化.雖然高中數學新課程已對一些內容降低了要求，但很多學生同樣不適應，不能很好地理解與掌握。高考試題中的三角函數題相對比較傳統，位置靠前，通常以簡單題形式出現。因此，在學習、復習過程中要特別注重三角知識的基礎性，突出三角函數的圖象及其變換、周期性、單調性、奇偶性、對稱性等性質，以及化簡、求值和最值等重點內容的學習，要求學生熟練記憶和應用三角公式及其恒等變形，同時要注重三角知識的工具性.對此本人從幾個方面加以闡述，希望能夠幫助學生認識“三角函數”在數學中的地位，能較為全面地把握“三角函數”知識脈絡，學好三角函數知識，提高綜合能力.

一、解決角的問題是學好三角函數的前提

（一）解決好特殊角的三角函數值的求法

在初中，學生對0°～90°之間的特殊角（30°、45°、60°）的三角函數值已了如指掌，但到了高中，隨著角度的擴展，求與特殊角有關的角的三角函數值也隨之增多，如對120°、135°、330°、—30°等角的三角函數值的求法開始出現了混亂。如何解決這一問題呢？通過學習誘導公式，學生明白了求這一類角的三角函數值，看似眾多，其實都與0°、30°、45°、60°、90°的三角函數值有關，且只有符號的異同。因此幫助學生弄清誘導公式所概括的“奇變偶不變，符號看象限”這一規律，計算這一類角的三角函數值的問題也就迎刃而解。

（二）解決好角與角之間的關系

相當多的學生直觀地把cos（α+β） 化為cosα+cosβ-sinαsinβ用于計算，造成運算煩瑣或無功而返。究其原因是缺乏整體思想，沒有注意到對角的關系進行觀察、分析。事實上若清楚β=（α+β）-α，則問題迎刃而解。又如：

（三）解決好隱含條件的問題

解題是數學學習中的一個主要環節，它的一般過程是：問題條件→知識方法→結果，可見尋找問題條件是解題的第一步.可是在一些數學題中，它的某些條件較為隱蔽，需要經過反復推敲，剖析題意.挖掘題設隱含條件，所謂隱含條件，是指題中若明若暗、含蓄不露的條件，它們常常巧妙地隱蔽在題設的背后，不易被人們所覺察，或者極易被人忽視，而直接制約整個解題過程，三角函數在許多方面如定義、公式、三角函數值，條件等式中都存在著隱含條件。在解三角函數題時，常因未能發掘其隱含條件造成一開始解題就無法進行，或者解到某一個階段而陷入困境，或者造成解題失誤。

例3.設△ABC的內角A、B、C的對邊長分別為a、b、c，cos，求B.

二、熟記，靈活運用公式是學好三角函數的基礎

（一）熟練掌握三角變換的公式

很多學生剛開始學習三角函數時，因為三角函數的公式太多，而造成混亂。其實公式之間也有一定的內在聯系，比如誘導公式（k∈z）中，只需把“α”看成銳角，畫出的終邊表示在X軸正半軸、X軸負半軸、Y軸正半軸、Y軸負半軸中的哪一個，終邊在X軸上則函數名不變，終邊在Y軸函數名改變；終邊再按順時針還是逆時針轉一個銳角定象限，確定函數符號。掌握了誘導公式以后，就可以把任意角的三角函數化為0°～90°間角的三角函數。又如：以兩角和的余弦公式為基礎推導得出兩角和與差的正弦、余弦、正切公式，以及二倍角的正弦、余弦、正切公式，掌握這些公式的內在聯系及推導的線索，能夠幫助我們理解和記憶這些公式；同角三角函數的基本關系式是進行三角變換的重要基礎之一，它們在化簡三角函數式和證明三角恒等式等問題中要經常用到，必須熟記，并能熟練運用.這也是學好本單元知識的關鍵.

（二）靈活運用三角公式

熟練掌握三角變換的所有公式理解每個公式的意義，特征；熟悉三角變換常用的方法——化弦法、降冪法、角的變換法等；并能應用這些方法進行三角函數式的求值、化簡、證明；掌握三角變換公式在三角形中應用的特點，并能結合三角形中的有關公式解決一些實際問題.

1.運用化弦（切）法：

2.運用增減倍與升降冪法：在運用公式化簡三角函數時，引導學生根據具體問題分析采用增倍還是減倍，升冪還是降冪。

因為函數f（x）在x=π處取最小值，所以sin（x+φ）=-1，由誘導公式知sinφ=1，因為0＜φ＜π，所以

例7：已知函數f（x）=sin2x+sinxcosx+2cos2x，x∈R.求函數（fx）的最小正周期和單調增區間；其中sinxcosx可轉化為sin2x，所以將sin2x、cos2x降冪同時把角轉化二倍角。

3.運用輔助角及常用模式的轉換法。在三角函數中除了運用課本內的公式外，還利用類似輔助角公式asinθ+bcosθ=進行解題。（這里輔助角φ所在象限由a、b的符號確定，φ角的值由tanφ確定。）而且在實際解題中，這一類問題大部分集中在sinα±cosα=cosα和等常用模式的轉化。

如上例7函數化簡為：

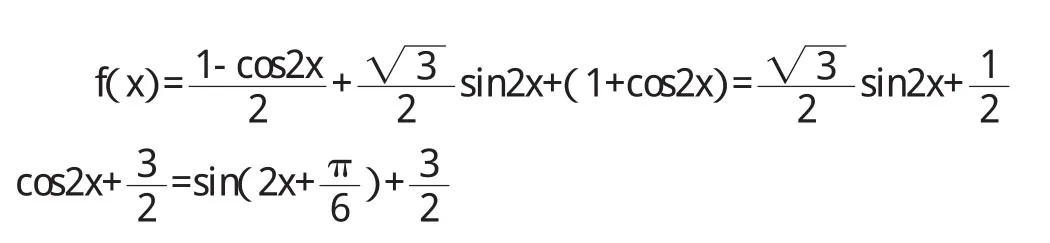
總之，只要我們讓學生注重三角函數的基礎知識，熟練掌握三角函數的圖象、性質，學會運用化歸轉化、分類討論、數形結合思想等思想方法解決問題，那么學生將會順利學好三角函數，使數學真正成為形成學生的理性思維和促進學生個人智力發展的動力，在提高學生的數學素養中，發揮出獨特的不可替代的作用。