甲板開口圍緣扁鋼加強方式研究

李霞麗，張世聯，李敏

上海交通大學船舶海洋與建筑工程學院，上海 200204

0 引 言

因總體布置需要，甲板通常具有較大的矩形開口。而開口容易破壞結構的連續性，使甲板變成間斷構件，致使甲板剖面上的應力重新分配，特別是在開口角隅處，會引起應力的高度集中，因而是船舶設計者十分關注的問題。為降低開口處的應力集中，通常采取的措施有：增加開口角隅板厚或貼板加強［1-2］、增大角隅圓弧半徑［3-4］或改善角隅形狀［5-10］，以及加設圍緣扁鋼［11-12］等。對于前兩種措施，已有較多文章探討過，而對圍緣扁鋼加強方式的研究則相對較少，尤其是在甲板大開口但沒有使用甲板端梁的情況下，圍緣扁鋼的尺寸參數對加強效果的影響明顯。本文將采用有限元法研究不同甲板尺寸和角隅半徑時，扁鋼尺寸參數的變化對開口處應力集中的影響，并基于最小應力集中系數（SCF）和最小結構重量的原則，進行開口處圍緣扁鋼加強方式的優化設計。

1 甲板開口模型

本文以某船主甲板上一矩形開口為研究對象，根據對稱性取半寬模型，沿船長方向取一個艙段范圍，甲板尺寸為24.8 m×15.3 m。考慮到在總縱彎曲作用下甲板受到的主要是面內載荷作用，此時，加強筋主要提供承載面積；而且通過對比同樣板厚情況下有甲板骨材和沒有甲板骨材兩種甲板開口受外力作用后的應力分布及應力集中效應，發現熱點應力集中在甲板骨材之間的甲板開口角隅邊緣上，骨材對應力集中的影響比較小；因此，將甲板上的骨材等效為板厚。等效后，甲板厚度td=14 mm，開口位于距中縱剖面6 m位置處，尺寸為2a×2b=7.7 m×2.7 m，開口角隅處采用圓弧過渡，半徑r=300 mm。甲板的材料為Q235鋼，彈性模量E=206 GPa，泊松比 μ=0.3。有限元計算模型如圖1所示，模型中橫剖面約束x和z向位移，中縱剖面處約束y和z向位移。模型兩端施加σ0=120 MPa的拉應力。甲板采用四邊形殼單元模擬，對開口周圍網格進行局部細化，尺寸為50 mm×50 mm，外圍區域網格尺寸為800 mm×800 mm。

2 未加強時的計算結果

根據計算，甲板開口未加強時的應力分布如圖2所示，其分布特點是：短邊上受壓，應力較小；長邊上受拉，應力較大，并逐漸向外遞減；4個開口角隅處會產生較大的應力集中，最大應力位置為圓弧與長邊的相切點。Von Mises應力最大值σmax=369 MPa，取甲板上遠離開口處的平均拉應力σ0為基準應力，則應力集中系數為

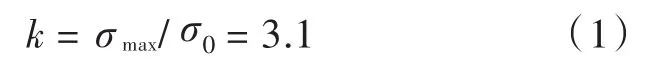
3 全范圍圍緣扁鋼加強

當外載荷以及開口尺寸一定時，對開口全范圍采用圍緣扁鋼加強。開口處的應力值主要與甲板的厚度td、扁鋼的寬度br及厚度tr相關，可將開口處的應力集中系數表達為

圖2 未加強時開口角隅處應力分布Fig.2 Stress distribution on deck around the opening corners without reinforcement

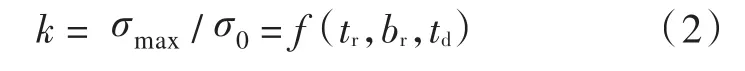
可將圍緣扁鋼的應力集中系數k定義為最大應力與甲板平均應力進行無量綱化作為其應力集中的度量，以便與甲板上的應力集中系數做橫向比較。

所謂全范圍加強，即繞開口內緣貼一整圈扁鋼取br=100～500 mm，每隔100 mm計算一個模型；取tr=10～30 mm，每隔1 mm計算一個模型。扁鋼單元大小取為50 mm×50 mm，研究開口處應力集中系數k隨br和tr變化的規律。

圍緣扁鋼加強時開口角隅處的應力分布如圖3所示。短邊上應力較小，長邊上應力較大，遠離角隅處的應力值逐漸減小；開口4個角隅仍出現較大的應力集中，但全局應力最大值的位置發生了變化，出現在了圓弧邊緣靠近轉角點處。

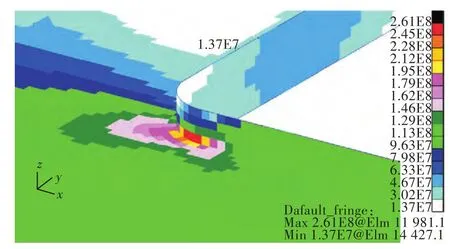
圖3 圍緣扁鋼加強時開口角隅處應力分布Fig.3 Stress distribution on deck around the opening corners attached ring plate

上述現象的原因可以通過其受力進行分析。圍緣扁鋼加強時，由于扁鋼對于甲板開口周圍的變形產生了約束，開口相連處除了沿開口的周向應力之外，還會產生較大的徑向應力，從而由單向應力狀態變為雙向應力狀態［12］。此時，最大應力不再只出現在最大周向應力位置，而是在周向應力與徑向應力共同形成的最大相當應力位置點，此位置偏離圓弧與長邊的切點處，更靠近轉角點，其具體位置與甲板和扁鋼的剛度相關。

3.1 扁鋼厚度、寬度的影響

在開口處采用圍緣扁鋼加強，應依據使開口區域應力集中系數k最小的原則確定最適宜的扁鋼尺寸（tr-opt，br-opt）。

在td和br一定時，甲板和扁鋼上的應力集中系數k隨扁鋼厚度比tr/td的變化趨勢如圖4所示，隨著tr的增加，圍緣扁鋼上的k逐漸減小，甲板上的k則是先減小后增大；開口區域的k先減小后增大，最大應力位置由甲板過渡到扁鋼上，k在tr/td=1.43，即tr-opt=20 mm時最小，kmin=2.16，應力集中水平降低約30%。

td一定時，不同扁鋼寬度br下開口處的應力集中系數k隨tr/td的變化趨勢如圖5所示，br越大，k越大；最佳tr-opt隨br的增加而逐漸減小。

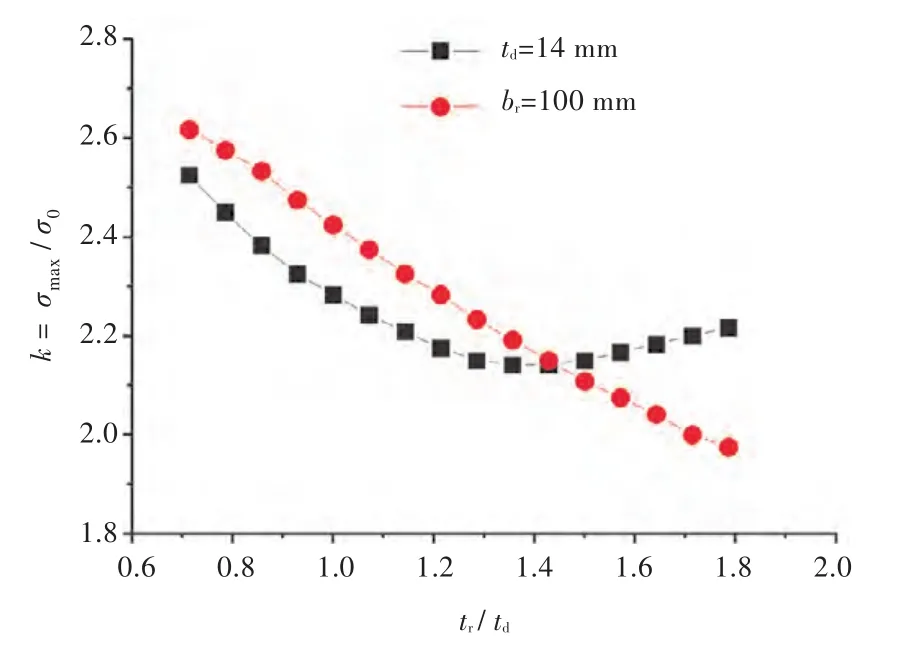
圖4 甲板及圍緣扁鋼上應力集中系數k隨tr/td的變化曲線Fig.4 Stress concentration factor（SCF）k on deck and ring plate versus tr/td

圖5 不同br時開口處k隨tr/td的變化曲線Fig.5 SCF k versus tr/tdwith br=100～500 mm

不同td和tr下，開口處k值隨br變化的趨勢如圖6所示。可以看出最佳br-opt受tr和td影響不大，均在br-opt=100 mm時取得最小的應力集中系數。

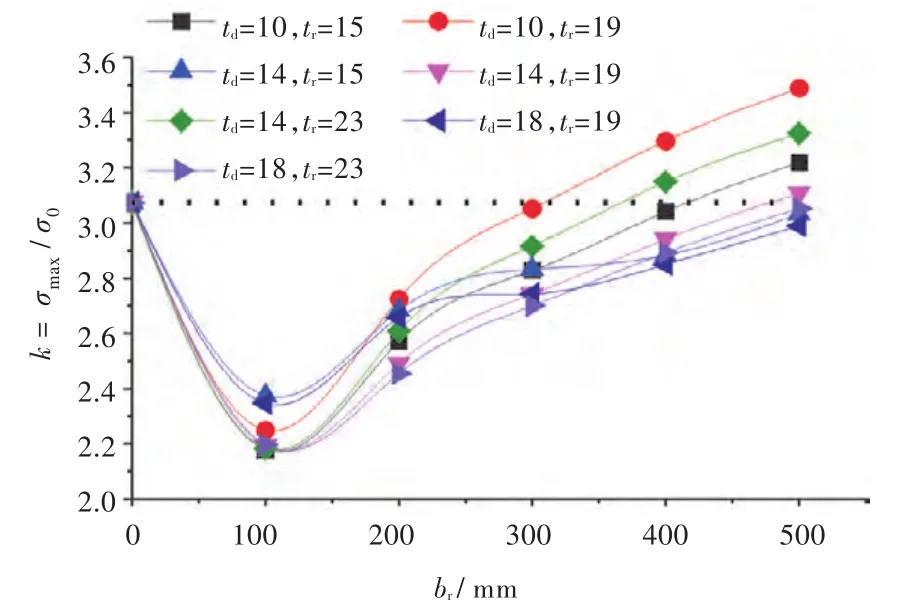
圖6 不同td和tr時，開口處k隨br的變化曲線Fig.6 SCF k versus brwith different td，tr

從其受力變形進行分析，甲板受到面內拉應力作用時，角隅處的圍緣扁鋼變形如圖7所示。扁鋼在與甲板連接處隨甲板一起發生了拉伸變形，上、下邊緣為自由邊，不受外力作用，相對于連接處便發生了受壓作用的皺折現象。這種皺折變形在圓弧止端達到最大，使扁鋼不能有效承擔外載荷，扁鋼及與其相連的甲板上應力分布發生變化，應力值大幅提高。

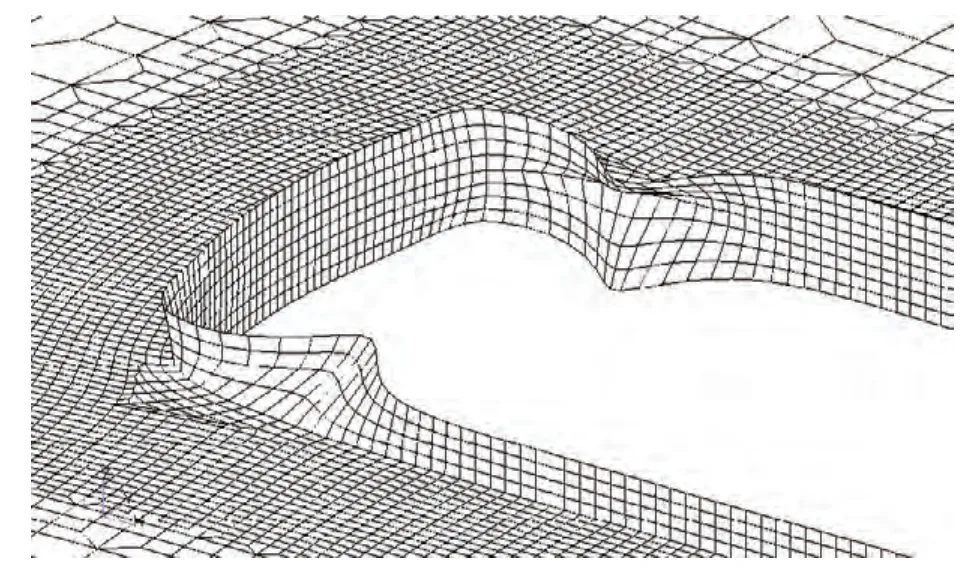
圖7 開口處變形示意圖Fig.7 Deformation around the opening corners

當tr/td超過一定數值后，扁鋼越厚，剛性越強，甲板受到共同變形的牽引作用便越大，應力值反而增加。扁鋼越寬，其柔性越大，皺折現象越嚴重，對應的應力值便越大，當寬度超過一定值后，不僅不能改善應力集中，反而會出現負效應，使得應力集中更顯著（圖6中虛線以上部分）。

由現有的經典結構力學知識可知，甲板開口的應力集中與r/a以及r/b數值相關［1］。本文保持角隅圓弧半徑r不變，變換開口長寬a和b值，研究不同開口尺寸下，開口處應力集中系數k隨扁鋼寬度br的變化規律，如圖8所示。由圖8可以看出，應力集中系數均在br-opt=100 mm時達到最小，說明最佳扁鋼寬度受開口尺寸的影響不大。通過進一步變換扁鋼寬度值（在0～100 mm（間隔10 mm）之間），發現扁鋼寬度在50～100 mm之間時應力集中系數最小，此時既不會產生明顯的皺折增加應力值，又能減小應力集中。隨著不同的開口尺寸變化，發現最佳扁鋼寬度在50～100 mm之間變化，但應力集中變化不大，此時扁鋼厚度是比較大的影響因素。實際應用中，可將br-opt=100 mm作為最佳扁鋼寬度設計值。

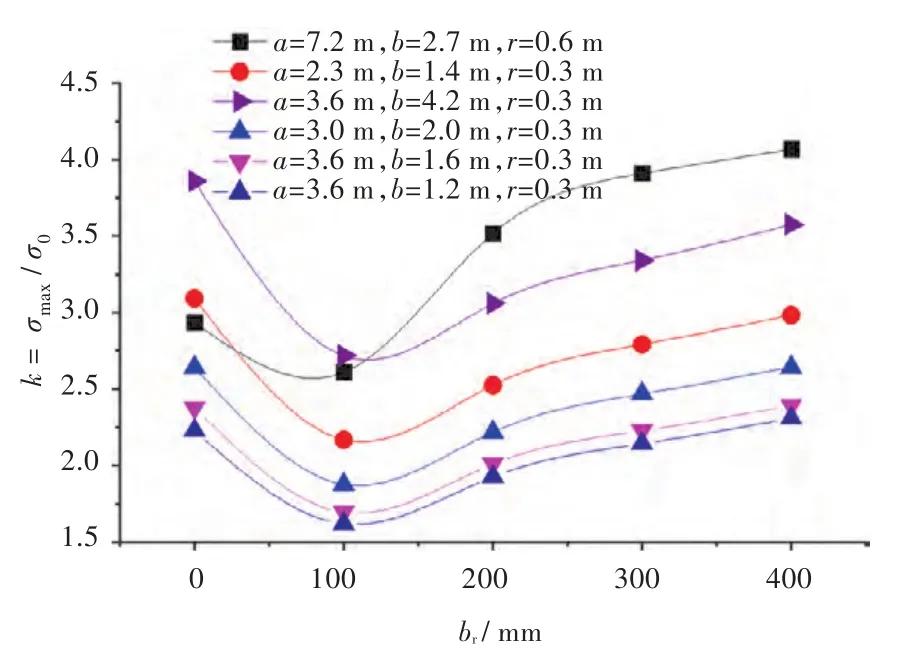
圖8 不同開口尺寸時，開口處k隨br的變化曲線Fig.8 SCF k versus brwith different opening sizes

3.2 扁鋼寬度、厚度的優化設計

由第3.1節的分析可知，增加扁鋼的寬度和厚度不一定能減小開口處的應力集中，應從最小應力集中系數出發對圍緣扁鋼進行優化設計，選取合適的扁鋼尺寸，以便獲得最佳的應力集中改善效果。

由文獻［1］可知，當未加強時，甲板開口時影響應力集中系數的主要因素是角隅半徑r與開口寬度b之比，r/b增大時應力集中系數急劇減小。扁鋼最佳板厚是r/b和甲板板厚td的函數。

確定tr-opt的方法有圖譜法和經驗公式計算法。

變換角隅圓弧參數 r/b（0.14～0.5）時，開口處應力集中系數k關于td和tr的曲線圖譜如圖9所示。確定扁鋼寬度后，根據甲板開口角隅圓弧參數r/b和甲板板厚td，再結合圖譜便可以確定最佳扁鋼厚度tr-opt，并可通過線性插值得到敷設該尺寸的圍緣扁鋼加強時能達到的最小應力集中系數。

此外，通過參數化分析發現，當r/b一定時，tr-opt與td基本呈線性關系，如圖10所示。線性擬合可得到tr-opt計算式（3），式中，參數m和n查表1得出。在最佳扁鋼厚度下，不同甲板厚度td時開口處的最小應力集中系數kmin隨r/b的變化趨勢如圖11所示。可以看出，kmin基本不隨td變化，僅由角隅圓弧參數r/b決定，隨著r/b的增大，應力集中系數迅速降低。可以認為kmin是r/b的單值函數，其關系可由式（4）表達。

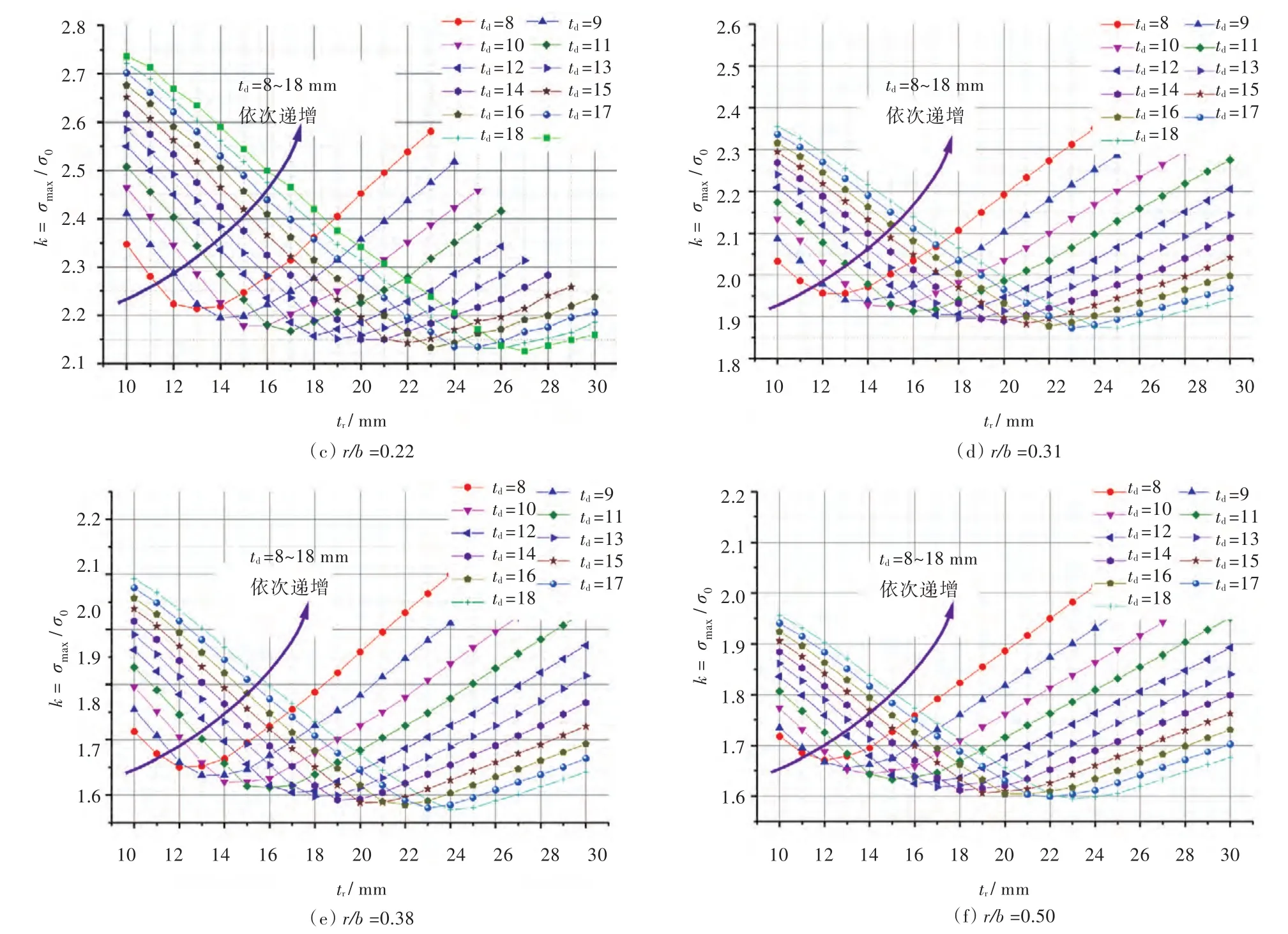
圖9 不同角隅圓弧參數r/b下，開口處應力集中系數k關于td，tr圖譜Fig.9 SCF k versus tr，tdwith different r/b

圖10 不同r/b時tr-opt關于td的曲線圖Fig.10 tr-optversus trwith different r/b

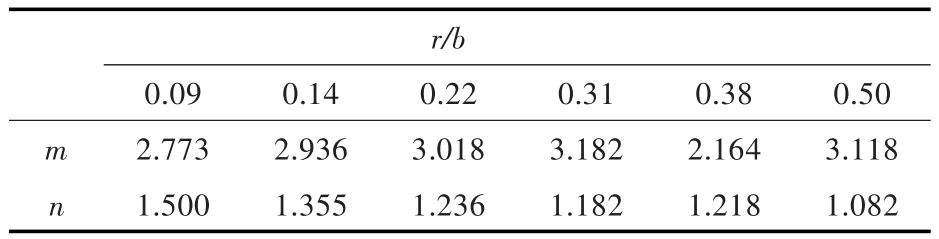
表1 不同r/b時的m和nTab.1 m，n with different r/b

圖11 不同td時開口處kmin關于r/b的變化曲線Fig.11 SCF k versus r/b with different td

3.3 實例驗證

為驗證式（3）和式（4）以及圖譜的適用性，選取一塊21.6 m×14.7 m的甲板，板厚為12 mm，甲板開口尺寸為2a×2b=4.5 m×1.4 m，角隅處圓弧半徑r=300 mm，r/b=0.43，扁鋼寬度為br-opt=100 mm，施加140 MPa的拉應力作用，進行計算分析。通過式（3）和式（4），計算得到扁鋼板厚（m和n分別通過線性插值取得）以及對應的應力集中系數為：

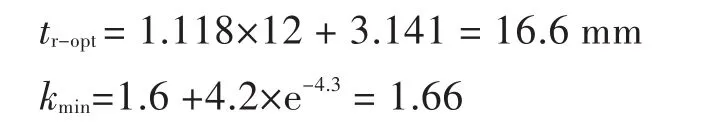
圍緣扁鋼最佳板厚為16.6 mm，此時應力集中系數為1.66，即最大應力值為232 MPa，同樣由圖9（e）和圖9（f）也可以估算出對應值。通過有限元數值計算，得到開口處最大應力值σmax和應力集中系數k隨扁鋼厚度tr的變化如表2所示。通過計算，得到tr=16 mm時應力集中系數最小，為1.71。最佳板厚和應力集中系數與提出的設計公式以及圖譜所得值吻合較好，誤差在3%左右。

表2 不同tr時開口處的k，σmaxTab.2 k，σmaxaround corner with different tr

4 局部圍緣扁鋼加強

由圖2～圖3的應力云圖可以看出，不管是加強還是未加強時，都僅在開口角隅處出現了應力集中，在遠離角隅的位置應力迅速衰減，扁鋼加強效果較小。從節省鋼料的角度出發，可以考慮只在應力集中的局部位置進行圍緣扁鋼加強的優化設計。

4.1 短邊局部加強

甲板和開口尺寸不變，角隅圓弧和長邊均增設圍緣扁鋼，扁鋼尺寸取100 mm×20 mm，這是全范圍加強的最佳扁鋼尺寸。以開口角隅圓弧與短邊切點為起點，在短邊上依次取圍緣扁鋼長度lb=0～1 m，間隔0.1 m，計算甲板和圍緣扁鋼上的應力。開口局部加強時，在角隅處以及扁鋼止端均有應力集中現象，最大應力值出現在角隅圓弧與長邊連接相切處，應力集中系數隨短邊扁鋼長度變化的趨勢如圖12所示。由圖可知，隨著開口短邊上圍緣扁鋼長度的變化，開口處應力集中系數幾乎不變。由此可以得出，短邊上的圍緣扁鋼對改善角隅應力集中貢獻比較小，可以根據實際結構設計和布置的需求，進而進行適當的截斷處理，進行優化設計。

圖12 開口處k隨短邊長度lb的變化曲線Fig.12 SCF k versus lb

4.2 長邊局部加強

在同樣的開口尺寸和甲板尺寸下，以開口角隅圓弧和長邊切點為起點，在長邊上取圍緣扁鋼長度la=0～3 m，間隔0.2 m，計算甲板和扁鋼上的應力。開口區域的應力分布如圖13所示，從中可見，在開口角隅處和和扁鋼止端均出現了較大的應力集中現象。

圖13 圍緣扁鋼長邊局部加強時開口區域應力分布Fig.13 Stress distribution on deck around the opening with local reinforcement on the long side

開口區域和角隅處的應力集中系數k隨la/a的變化趨勢如圖14所示。由圖可見，長邊局部加強時，隨著扁鋼長度的增加，開口角隅處k逐漸增大，扁鋼止端k逐漸減小。

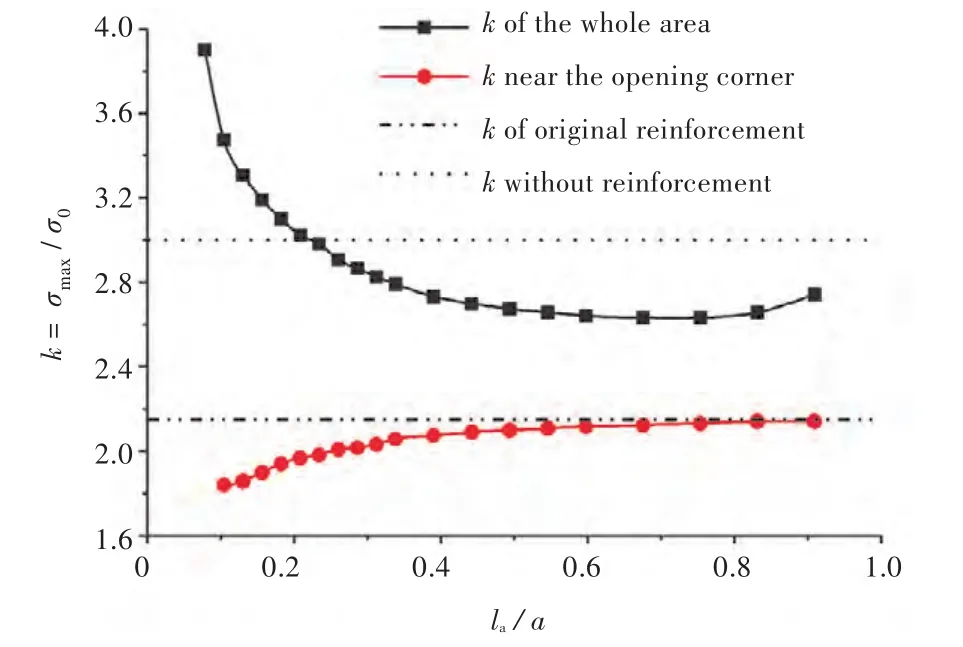
圖14 開口角隅處和扁鋼止端k隨扁鋼長度la/a變化曲線Fig.14 SCF k around the corner and at the end of the ring plate versus la/a

扁鋼止端k始終大于開口角隅處的k值，說明最大應力值始終出現在扁鋼長邊止端與甲板相連處。當開口長邊上扁鋼長度較短，即扁鋼止端接近角隅時，由角隅本身形狀突變引起的應力集中和由圍緣扁鋼中斷引起的應力集中疊加，會產生很大的應力；當圍緣扁鋼止端延伸至遠離角隅處時，兩種應力集中因素錯開，分別在角隅處和扁鋼止端產生應力集中，從而使得整體應力集中水平下降。

由以上分析可知，采用圍緣扁鋼進行局部加強時，應避免在開口的長邊上斷開。扁鋼在長邊上斷開，形成的新的間斷構件會產生附加的應力集中，不僅不能增強開口處的結構強度，反而會增加應力集中水平。在實際應用中，即使需要在長邊上打斷圍緣扁鋼，也應避免在開口角隅附近終止。適當地延長扁鋼長度至開口長度的20%（圖14中，la/a=20%時應力集中系數達到最小并趨于平穩），便能有效降低應力集中水平。

5 結 論

通過研究對不同尺寸的甲板及其矩形開口采用圍緣扁鋼加強時，扁鋼尺寸參數對開口處應力集中的改善效果，得到以下結論：

1）通過敷設適當尺寸的圍緣扁鋼加強可以有效降低甲板開口角隅處的應力集中。

2）敷設扁鋼使開口處的應力變為雙向應力狀態，扁鋼尺寸并非越大越好，當寬度和厚度增加到一定數值后反而會造成更大的應力集中，應力集中系數隨扁鋼尺寸的增大是先減小后增大，需要從最小應力集中的角度出發對圍緣扁鋼進行合理設計。

3）扁鋼的最佳寬度值通常在50～100 mm之間，最佳厚度是甲板厚度和角隅半徑參數的函數，采用式（3）和式（4）或設計圖譜，可以簡便、快速地得到合理的扁鋼厚度以及相應的應力集中系數。

4）從應力分析的角度來看，短邊上的圍緣扁鋼對改善應力集中的貢獻比較小，在實際結構布置允許的情況下，可以在圓弧切點處截止以優化設計。

5）圍緣扁鋼在長邊上中斷會產生較大的應力集中，應在全部長度范圍上連續敷設。若因布置的需要需在長邊上打斷圍緣扁鋼時，也應避免在開口角隅附近終止。扁鋼應延長至距離圓弧切點20%開口長度的位置以外，以避免產生過大的應力集中。

［1］楊代盛.船體強度與結構設計［M］.北京：國防工業出版社，1986.

［2］中國船級社.鋼質海船入級與建造規范［S］.北京：人民交通出版社，2010.

［3］趙建華，吳劍國，俞銘華.艦船甲板大開口應力集中的理論分析［J］.華東船舶工業學院學報（自然科學版），1996，10（4）：15-19.ZHAO Jianhua，WU Jianguo，YU Minghua.Theoretical analysis of stress concentration in a large deck opening［J］.Journal of East China Shipbuilding Institute（Natural Science Edition），1996，10（4）：15-19.

［4］王林，吳劍國，俞銘華，等.船體甲板和側壁大開口應力集中及其加強形式［J］.華東船舶工業學院學報（自然科學版），1998，12（3）：59-64.WANG Lin，WU Jianguo，YU Minghua，et al.Stress concentration of large opening in the deck and the sideboard of ship and its strengthening measures［J］.Journal of East China Shipbuilding Institute（Natural Science Edition），1998，12（3）：59-64.

［5］FRANCAVILLA A，RAMAKRISHNAN C V，ZIENKIEWICZ O C.Optimization of shape to minimize stress concentration［J］.The Journal of Strain Analysis for Engineering Design，1975，10（2）：63-70.

［6］KRISTENSEN E S，MADSEN N F.On the optimum shape of fillets in plates subjected to multiple in-plane loading cases［J］.International Journal for Numerical Methods in Engineering，1976，10（5）：1007-1019.

［7］王承先，陶政國.船舶甲板開口角隅形式的研究［J］.艦船科學技術，1984，（11）：10-14.

［8］俞銘華，徐昌文.船舶艙口角隅最佳形狀的研究［J］.華東船舶工業學院學報（自然科學版），1988（4）：1-8.

［9］俞銘華，徐昌文.甲板矩形開口角隅形狀優化設計和光彈性試驗［J］.中國造船，1991（2）：45-55.

［10］蔡乾亞，楊永謙，裘泳銘.集裝箱船艙口角隅的應力集中及其結構形式［J］.上海交通大學學報，1996（8）：125-129.

［11］吳家龍，何穎強，吳群益.純彎梁加環孔邊應力分析［J］.同濟大學學報，1983（3）：83-95.

［12］夏志皋.加強孔口應力集中系數的合理定義［J］.上海力學，1990（1）：81-84.