數字控制電壓調整器模塊的建模分析

1 引言

適用于未來微處理器的電壓調整模塊（Voltage RegulatorModule,VRM）是一種特殊的負載點（PointofLoad,POL）變換器，它有很高的性能要求：低輸出電壓（0.8～1.6V），高負載電流（可達150A）以及快速的動態響應（負載電流變化率可達2A/ns）[1,2]。

現如今，主流的VRM電路拓撲是多相的Buck變換器[3-5]。但是，隨著開關頻率的提高，傳統的多相Buck變換器會遇到很多問題：開關損耗高、驅動損耗高以及同步整流管的體二極管損耗高等。所以，為能使工作在較高開關頻率時有相對較高的效率，文獻[6]提出了一種運用在VRM上的零電壓開關（ZeroVoltageSwitching,ZVS）自驅非隔離全橋變換器。所有的MOS管都實現ZVS以減少開關損耗。變壓器的引入使變換器占空比得到拓展，導致MOS管開關損耗和體二極管反向恢復損耗進一步降低。同步整流管（SynchronousRectifier,SR）自驅的觀念，即變壓器二次電壓或其電壓的一部分用作整流管的驅動已被廣泛運用[7-10]。同步整流管自驅的好處是：驅動電路簡單、部分驅動的能量可再利用以達到低損耗，高效率的目的等。

雖然在低壓、大電流、高頻率的運用場合，現在仍多使用傳統的模擬控制器，但隨著電力電子技術的不斷發展，功率變換器向著小型化、模塊化和智能化發展[11,12]。傳統的模擬控制已不能滿足要求，因此數字控制變換器是發展的必然趨勢。數字控制器是個很有前景的研究課題，它自身有很多優勢：可編程、低功耗、可節省空間的使用、控制器整體的魯棒性好，即對寄生參數變化不敏感、易于實現先進和復雜的控制策略等。為了提高功率密度和動態特性，變換器的開關頻率越來越高，目前已達1MHz甚至更高。超高的開關頻率會給數字控制帶來新的問題。由于量化誤差的存在，可能產生有限環振蕩，影響系統的穩定性。另外，由于數模轉換器（Analog to Digital Converter, ADC）采樣時間和數字電路計算時間的存在，反饋系統中存在比較大的時間延遲，如果不能很好的建模和補償，會嚴重損害系統的動態特性。本研究是在目前數字電路小信號模型的基礎上，研究反饋回路上每一個環節對時間延遲的影響，從整體上得到一個完整準確的數字控制變換器小信號模型，以此來指導整個變換器控制補償的設計[13-17]。

數字控制的12VZVS自驅VRM包括了主電路和控制電路，其中主電路部分是一個模擬系統，而數字控制部分是數模混合系統。圖1給出了數字控制VRM的系統框圖，點劃線部分是數字控制器的內部結構。電壓和電流的ADC會將采樣回來的電壓和電流模擬信號轉換成離散值，所有的補償和計算等都是在數字的離散形式下完成的。然后通過數字脈寬調制器（Digital Pulse Width Modulation,DPWM），將離散的占空比值再轉換成模擬信號用以驅動開關管。

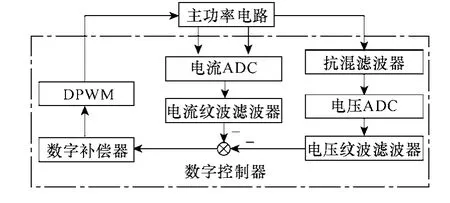
圖1 12VZVS自驅VRM的系統框圖Fig.1 System diagram of 12V ZVS self-driven VRM

因此要對數字控制VRM進行很好的控制，必須對其主電路和控制電路進行建模分析。另外還設計了自適應電壓定位（Adaptive Voltage Positioning，AVP）環路以保證電路實現AVP。

本文將詳細給出數字控制12VZVS自驅VRM的主電路和數字控制電路的小信號模型，并依此設計AVP環路，再通過仿真和實驗結果來驗證此設計方法。

2 主功率電路小信號模型的建立

12VZVS自驅VRM的主電路（圖2）本質上是Buck型全橋直流變換器，它的小信號模型與多相Buck變換器類似。圖3給出了12VZVS自驅VRM與兩相交錯并聯Buck電路的對應關系。圖中，12V自驅VRM中的Q2和Q4管分別對應兩相Buck中的Q2和Q1管；同步整流管S1和S2分別對應到兩相Buck中的S1和S2管。另外，12V自驅VRM中，Q1和Q3管的驅動信號與Q2和Q4管的互補。

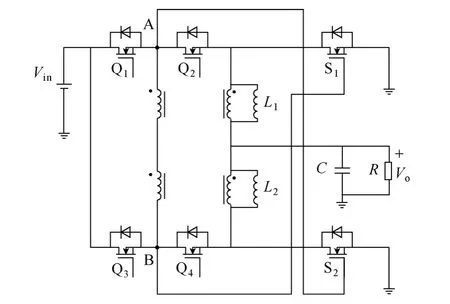
圖2 12V零電壓開關自驅電壓調整模塊Fig.2 12VZVSself-drivenVRM

圖3 兩相Buck和12V自驅VRM的比較Fig.3 Comparison between 2-phase Buck and 12V ZVSself-driven VRM

這兩個電路小信號模型的主要區別在于12V自驅VRM中存在變壓器的漏感，它的功能相當于一個阻尼電阻。由于采用PCB繞組，所以漏感值較小，其作用可以忽略。因此可以借鑒多相Buck主電路

模型推導的方式來推導12V自驅VRM主電路模型。

圖4是12VZVS自驅VRM的小信號模型。

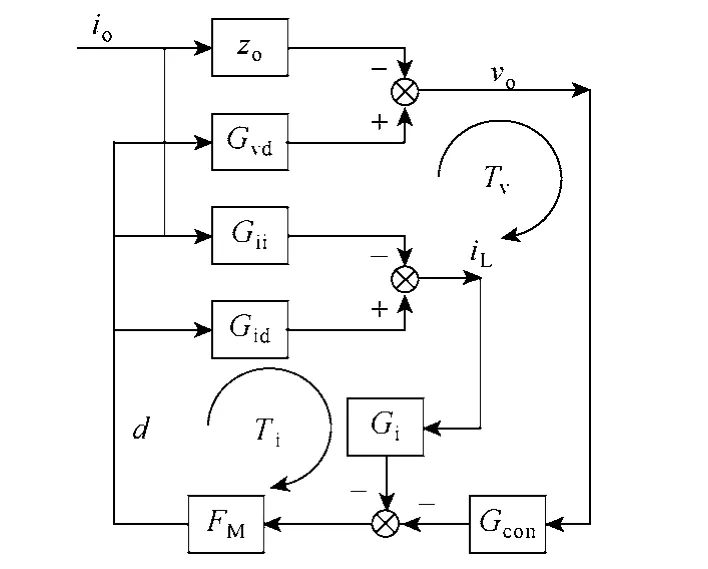
圖4 12VZVS自驅VRM的小信號模型Fig.4 Small signal model of 12V ZVS self-driven VRM

圖中，Gii是電感電流iL相對負載電流io的傳遞函數。Gid是電感電流iL相對占空比d的傳遞函數。FM模擬了電感電流的脈動效應。Gi代表電流的檢測，值通常取檢測電阻Ri。Gcon是電壓回路補償器的傳遞函數。

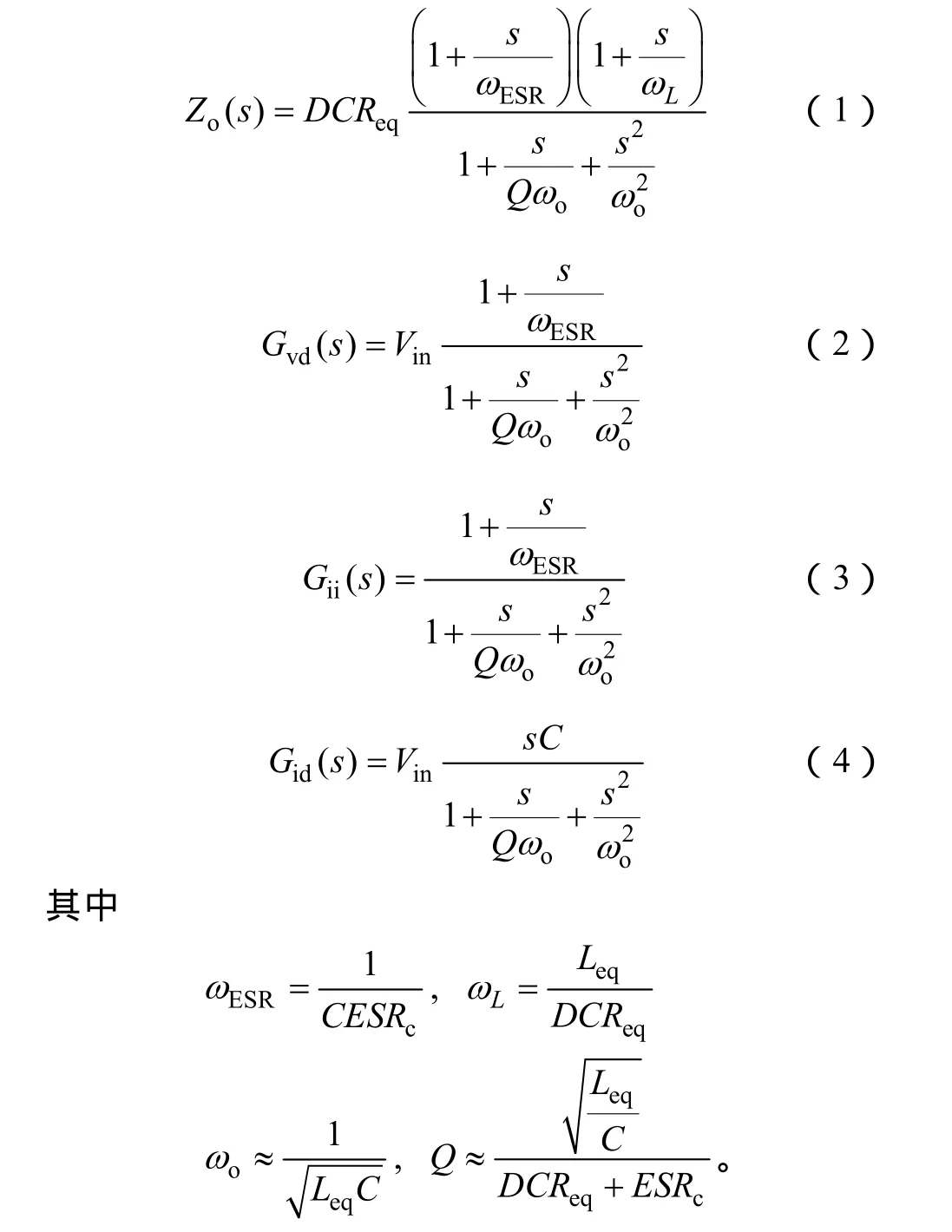
這里，Leq是等效的濾波電感，DCReq是其等效的直流電阻。由于是四相交錯并聯工作，因此Leq是單相濾波電感的四分之一，DCReq是單相直流電阻的四分之一。

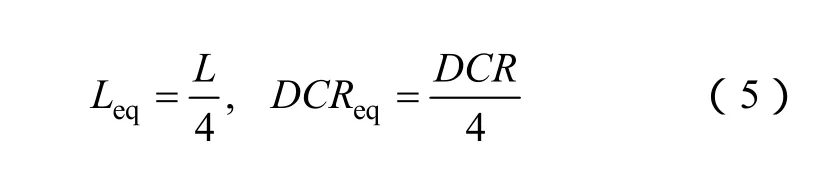
3 數字控制器小信號模型的建立

3.1 抗混濾波器小信號模型的建立

圖5給出了沒有限制帶寬的采樣信號頻譜圖。經過采樣之后，信號的基本頻譜會在采樣頻率的諧波頻率上重復延拓，諸如±fs，±2fs等。如果信號的頻譜不受限制，就會產生混疊效應。混疊效應會使得采樣后的信號修復變得困難。為減小這種效應的影響，加入了一個抗混濾波器。圖6給出了加入抗混濾波器后采樣信號的頻譜。這個濾波器的目的是消除采樣信號高于奈奎斯特頻率（采樣頻率的一半）的部分。數字控制器中，一階低通濾波器可用作抗混濾波器。它的傳遞函數表達式為

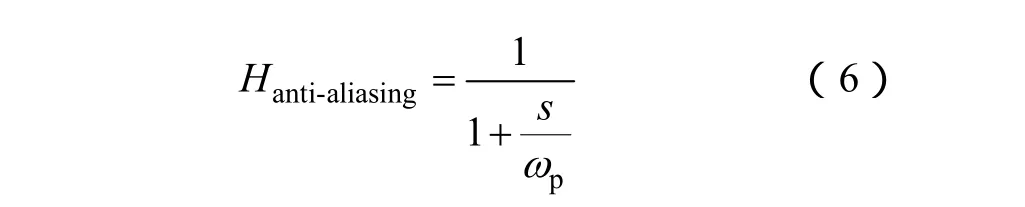
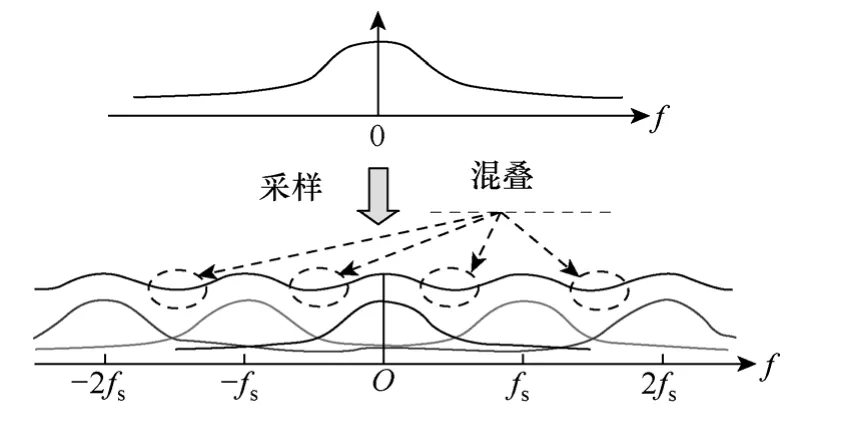
圖5 未限制帶寬信號的頻譜Fig.5 Spectrum of an unlimited band signal

圖6 加入抗混濾波器后信號的頻譜Fig.6 Spectrum of an unlimited band signal withanti-aliasing filter

3.2 電壓和電流ADC小信號模型的建立

圖1中電壓和電流采樣均需通過ADC將模擬信號轉換成數字信號，電壓和電流ADC的電路結構一樣。圖7是ADC的模型，它包括一個采樣器、一個延時器以及一個數字轉換器。

圖7 模數轉換器的經典模型Fig.7 Classical Model of an analog to digital converter

ADC的小信號模型可以分成兩部分。第一部分包括采樣和延時單元，表現出純粹的延時功能。而在整個數字控制系統中，不僅僅ADC存在延時，計算以及DPWM都存在延時，在此所有延時都統一起來考慮，其表達式如下

式中，Td表示整個數字控制系統的延時時間，即從輸出采樣到占空比作用的延時時間，包括ADC、計算以及DPWM時間。

數字補償器中，電壓和電流的采樣頻率是不同的。對于電壓ADC采樣頻率是開關頻率的兩倍，如圖8所示。采樣時刻都是在導通時間段和關斷時間段的中點。在這階段，假設模數轉換時間和計算時間足夠短，以至于采樣電壓在時刻nTs時，占空比會在緊接著的關斷邊緣更新。因此，稱這個延時為tdv1。同樣，當采樣時刻為(n+1)Ts，延時為tdv2。對小信號回路的分析，考慮這兩種延時的最壞情況。如

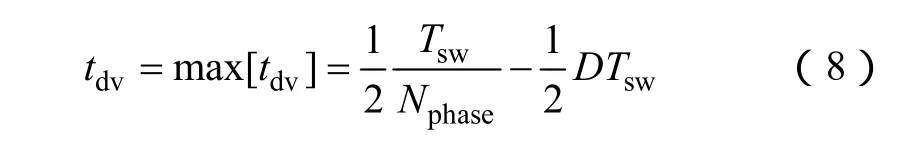
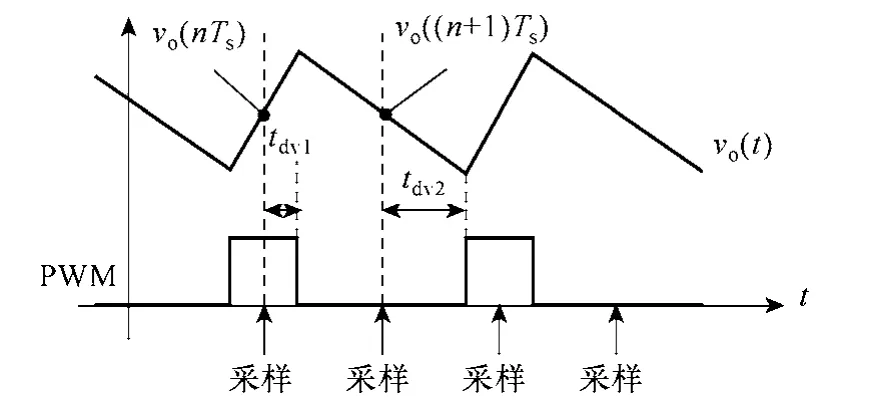
圖8 電壓模數檢測延時Fig.8 Voltage A-D sensing delay

對于電流ADC采樣頻率等于開關頻率。采樣時刻在每個開關關斷時間段的中點，如圖9所示。

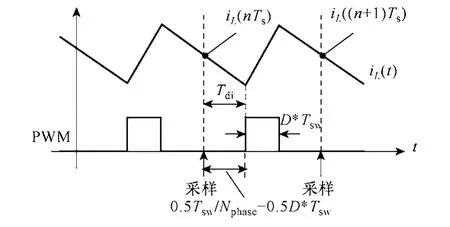
圖9 電流模數檢測延時Fig.9 Current A-D sensing delay

與電壓ADC推導的方法類似，電流回路的延時時間計算如下

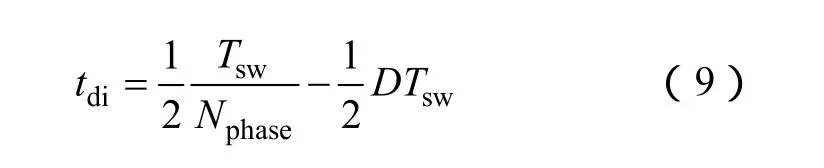
ADC包括一個數字轉換器。數字轉換器是一個非線性的模塊，它有非線性的增益。當擾動足夠大（相比于轉換器的階梯波幅值）時，非線性增益可簡化為線性的。故做出如下假設，數字轉換器的增益為一線性值，即

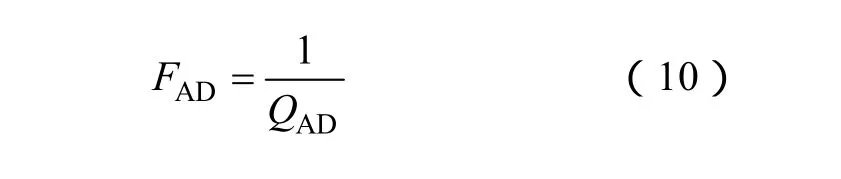
式中，QAD是轉換器的階梯波幅值。

對于電壓ADC，這個值通常是固定不變的。對于電流ADC，情況則有所不同。因為數控芯片內部會將檢測到的電流值重新轉換成它的真實值。例如，電感電流值是10A，考慮到檢測和采樣的增益，用于計算的電流信息設定為10A。在這情況下，電流ADC的整體增益就可以設定為1。

3.3 紋波濾波器小信號建模的建立

對于電壓回路，采樣頻率是開關頻率的兩倍。因此，采樣電壓仍會有開關頻率部分的噪聲，這是回路補償所不希望的。抗混濾波器是一階低通濾波器，其截止頻率大概在1MHz范圍，所以它不能消除開關頻率附近的紋波。為解決這個問題，引入了一個數字濾波器。

此濾波器的Z域傳遞函數如下

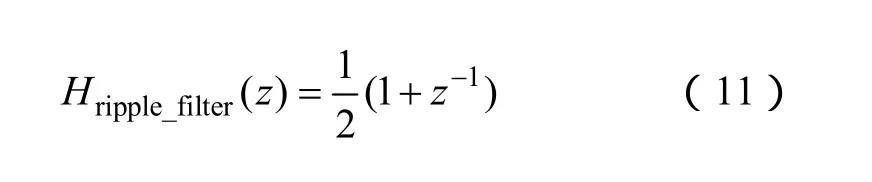
此濾波器的物理意義是將連續的兩個采樣值取平均。為得到它的等效S域傳遞函數，在此采用雙

其Z域和S域傳遞函數的伯德圖如圖10所示。

電流回路中電流紋波濾波器與其類似，這里不再贅述。

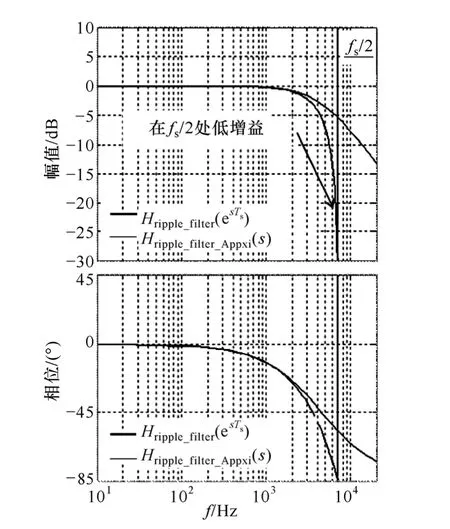
圖10 紋波濾波器Z域和S域伯德圖的比較Fig.10 Comparison of Bode plot of Z-domain andS-domain ripple filter

3.4 數字補償器小信號模型的建立

數字控制回路使用比例、積分、微分（PID）補償器來修正檢測的數字化電壓使其穩定在給定值。額外的二階微分增益和二階后置濾波器提供高階零、極點，進一步優化回路寬范圍的性能。所有回路參數在一定的范圍內是可編程的，允許的回路帶寬是10～300kHz，同時它也取決于主功率電路的形式。式（13）給出了一個通用的補償器的表達式。

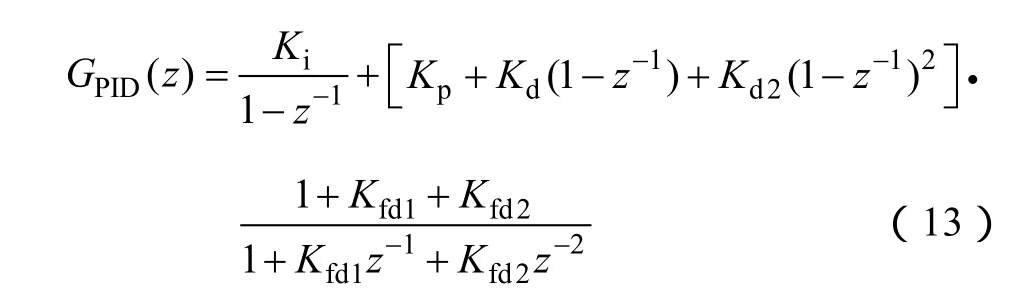
式中，Ki、Kp、Kd和Kd2分別是積分、比例、微分和二階微分增益；Kfd1、Kfd2是二階全極點低通后置濾波器的系數。

采用雙線性變換，等效的S域傳遞函數可推導如下

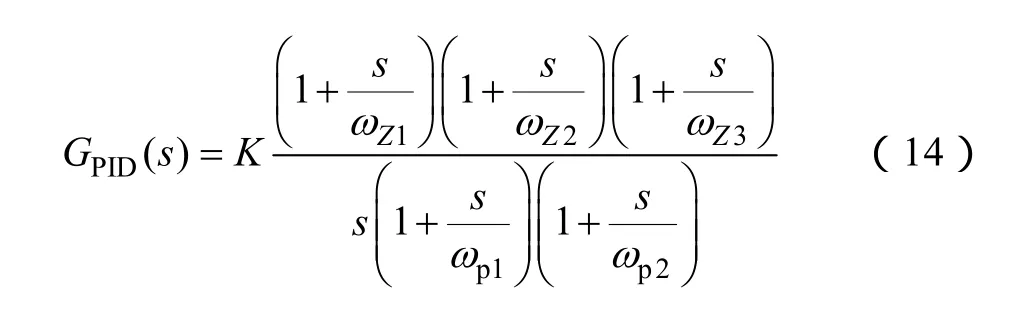
從式（14）可以看出，補償器實際上是一個三極點、三零點的補償器。

3.5 DPWM小信號模型的建立

控制電路中采用雙沿數字調制波。在小信號的分析，忽視非線性增益，將其視作為一個線性增益。圖11是DPWM的增益推導。

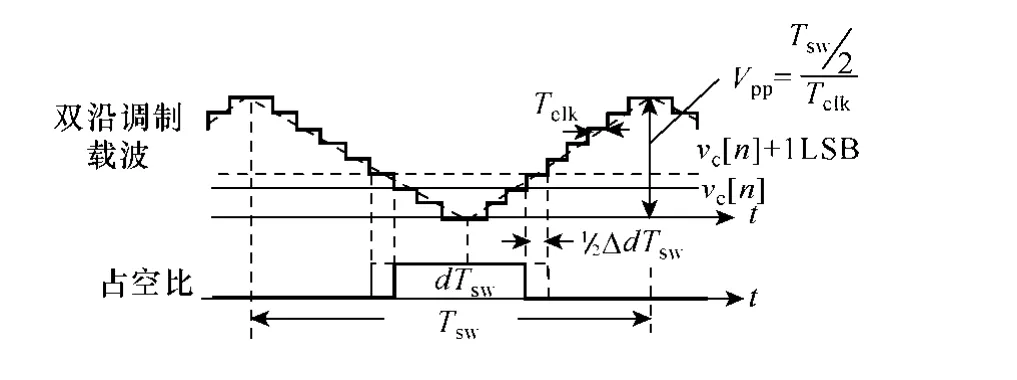
圖11 DPWM的增益推導Fig.11 Derivation of DPWM gain

與模擬的PWM推導類似，DPWM的增益如下

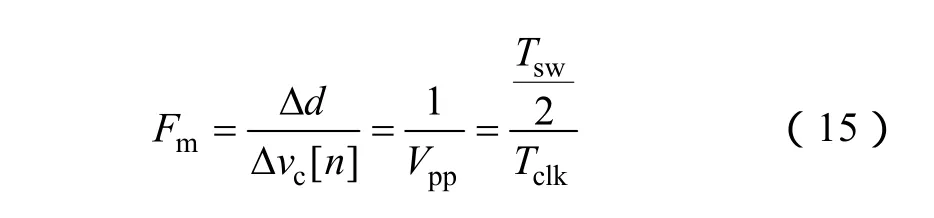
式中，Tsw是開關周期；Tclk是DPWM的分辨。

3.6 數字控制器完整小信號模型的建立

以上將數字控制電路各組成部分分別建模，依此圖12給出了完整數字控制器小信號模型。

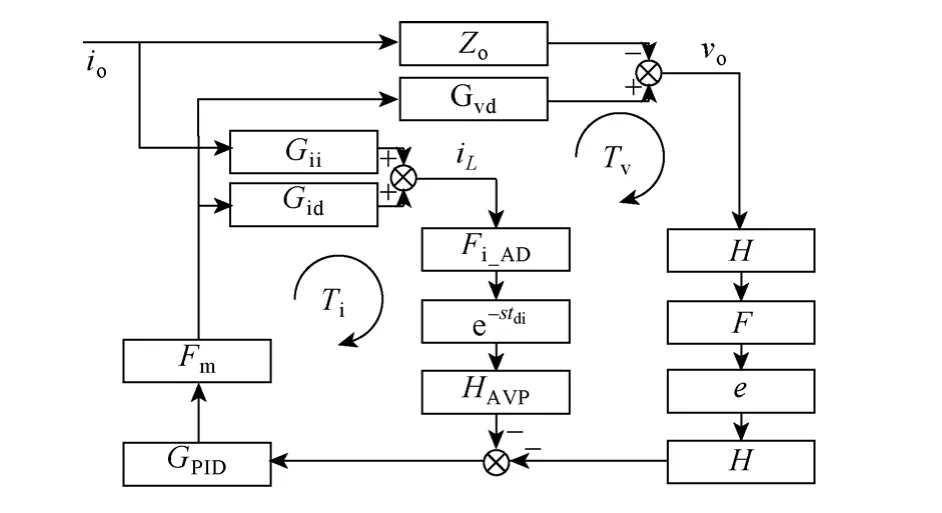
圖12 數字控制12V自驅VRM的小信號模型Fig.12 Small signal model of digitally controlled 12Vself-driven VRM

電流回路的增益是

電壓回路的增益（電流回路開路）是

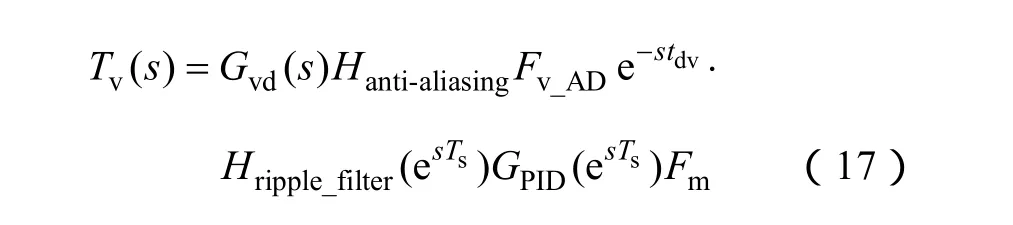
整個電壓回路的增益T2（電流回路閉合）是

4 自適應電壓定位設計方法

對于AVP回路的設計，借鑒了文獻[18]提出的恒定輸出阻抗設計概念。高帶寬的電流回路設計可將一個二階系統簡化成一階系統。當電流回路閉合及電壓回路開路時，變換器可當成一個理想的電流源，它的輸出阻抗近似表示如下

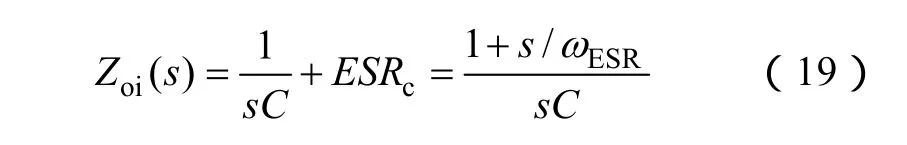
圖13是電流回路閉合時的電路圖，變換器因而簡化成一個一階系統。電流源的阻抗無窮大，故只有輸出電容會影響到系統的輸出阻抗。

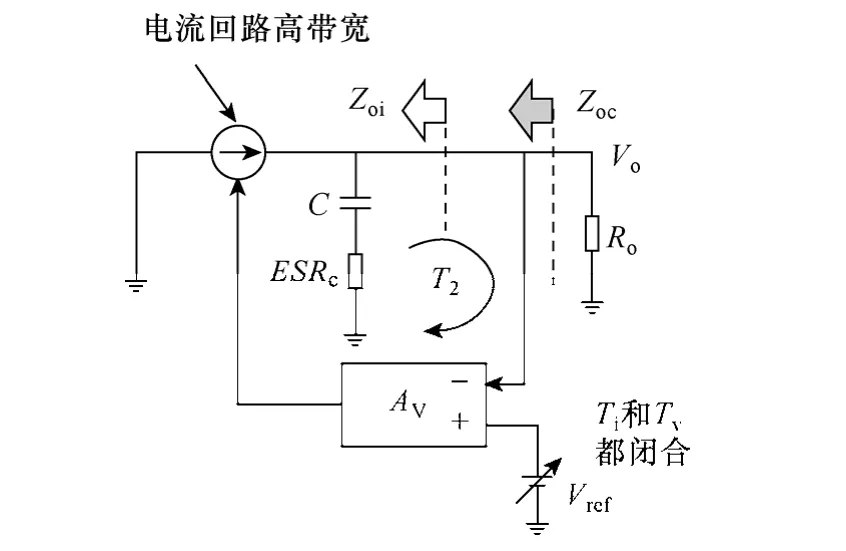
圖13 電流回路閉合12V自驅VRM電路圖Fig.13 Circuit diagram of 12V self-driven VRM withcurrent loop closed

圖14是恒定輸出阻抗設計示意圖。為了實現恒定的輸出阻抗，系統回路 T2應設計成斜率為-20dB/dec，截止頻率ωc由Rdroop值和全部的輸出電容決定。期望的T2是

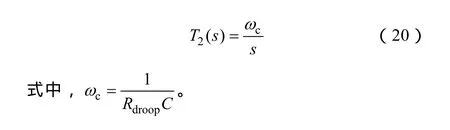
式（18）已經給出T2的表達式，將已知的表達式代入，聯立式（18）和式（20），可以得到補償器的確切表達式，并依此設計補償電路。一般的補償電路，只需要雙極點和單零點，形如

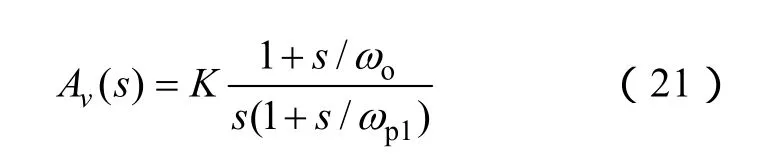
其中，積分環節是用來消除穩態誤差；零點是用來補償系統的雙極點；高頻域范圍的極點是用來進一步衰減開關噪聲的，但也可省略以簡化補償器的設計。設計K值，從而得到電流回路的高帶寬ωci。

圖14 恒定輸出阻抗設計Fig.14 Constant output impedance design

5 仿真和實驗結果

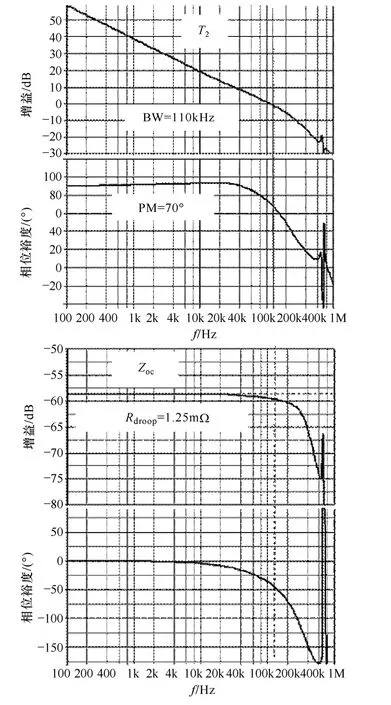
圖15 自適應電壓定位12V自驅VRM仿真結果Fig.15 Simulation results of 12V self-driven VRM with AVP

為驗證模型和設計策略，搭建了SIMPLIS仿真電路。圖15是T2的回路增益和閉合回路輸出阻抗的仿真模型。T2的帶寬是110kHz，相位裕度是70°，高于帶寬時輸出阻抗是恒定的。圖16是負載跳變（Io:0A→100A→0A）時域的仿真結果。

圖16 12V自驅VRM負載跳變的仿真結果Fig.16 Simulation results of 12V self-driven VRMof load transient

為了驗證理論分析的正確性，在實驗室制作了一臺實驗樣機，主功率電路的參數如表1所示。圖17是1UVRM樣機的圖片。圖18是實驗結果，控制帶寬是106kHz，相位裕度65°。圖19是負載跳變時實驗結果的時域波形。實驗結果表明，根據本文所提出的小信號模型，設計的電路控制參數可以滿足要求，實驗結果驗證了理論分析的正確性。這里輸出濾波電容的取值（2mF）較理論計算（1mF左右）的大。因為控制器的延時效應產生較大的電壓波動，而VRM對電壓的要求又很嚴格，沒有其他更好的方法消除，故只能增大輸出濾波電容。

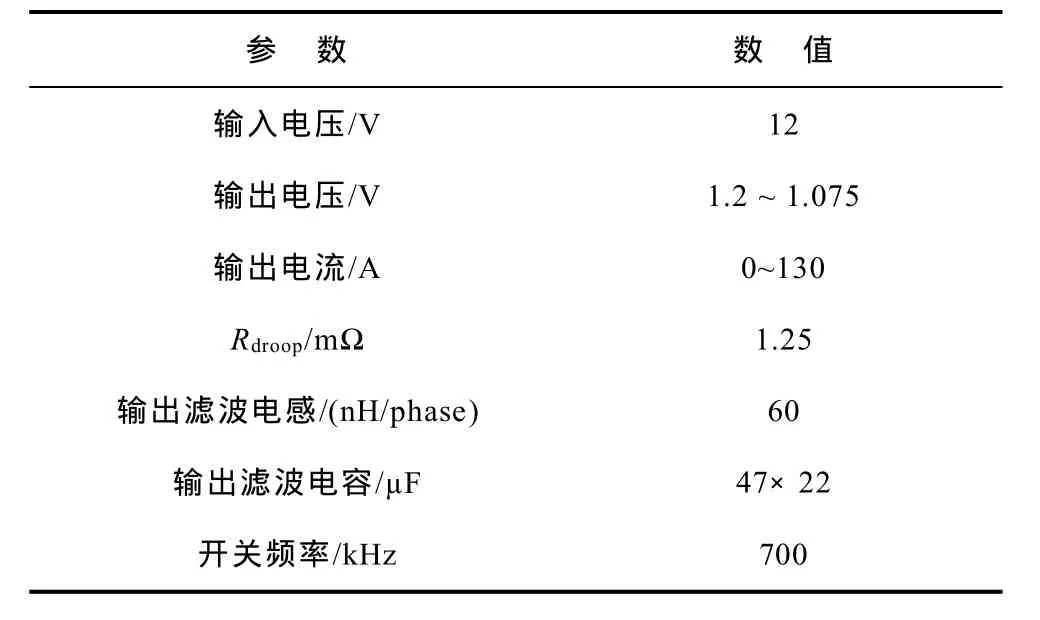
表 主功率電路參數Tab. Parameters of main circuit

圖17 原理樣機Fig.17 The prototype picture圖18

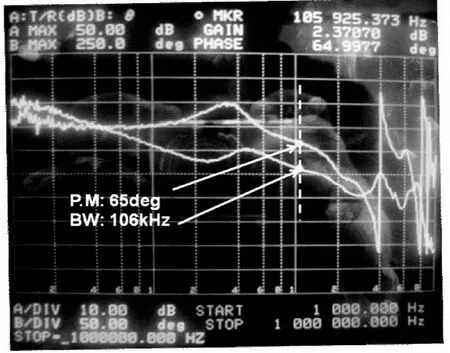
圖18 2mF電容的回路測量結果Fig.18 Loop measurement with 2mF capacitor

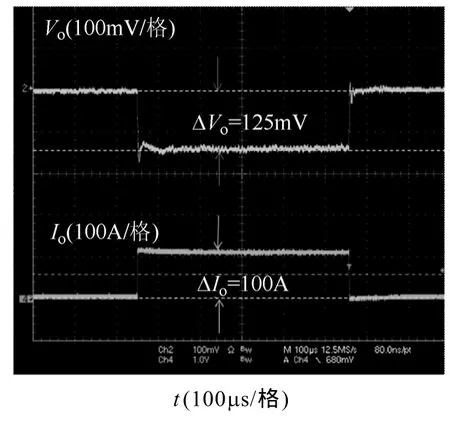
圖19 2mF電容的動態性能Fig.19 Load dynamics with 2mF capacitor

6 結論

本文提出了一種系統的數字控制VRM建模方法。對12VZVS自驅VRM的主電路和控制電路逐一進行建模，最后給出了完整模型。通過這種方法，可以更直觀地了解數字控制器。在此基礎上設計控制器并實現了AVP功能。這種方法準確、直觀。最后通過仿真及實驗結果很好地驗證了理論分析的正確性。

[1] Voltage regulator module(VRM) and enterprise voltageregulator-down(EVRD) 11.0 design guidelines[S].Santa Clara, CA: Intel Crop., 2006.

[2] Zhou X, Zhang X, Liu J. Investigation of candidate VRM topologies for future microprocessors[C]. Proceedingsof the IEEE APEC, 1998: 145-150.

[3] Yao K, Xu M, Meng Y, et al. Design considerationsfor VRM transient response based on the output impedance[J]. IEEE Transactions on Power Electronics,2003, 18(6): 1270-1277.

[4] Ren Y, Yao K, Xu M, et al. Analysis of the powerdelivery path from 12V VR to the microprocessor[J].IEEE Transactions on Power Electronics, 2004, 19(6):1507-1514.

[5] Zhang Z, Eberle W, Yang Z, et al. Optimal design ofresonant gate driver for buck converter based on anew analytical loss model[J]. IEEE Transactions onPower Electronics, 2008, 23(2): 653-666.

[6] Zhou J, Xu M, Sun J, et al. A self-driven softswitchingvoltage regulator for future microprocessors[J]. IEEE Transactions on Power Electronics,2005, 20(4): 806-814.

[7] Alou P, Cobos J A, Garcia O. A new driving schemefor synchronous rectifiers: Single winding self-drivensynchronous rectification[J]. IEEE Transactions onPower Electronics, 2001, 16(6): 803-811.

[8] Ren Y, Xu M, Sterk D, et al. 1 MHz self-driven ZVSfull-bridge converter for 48 V power pods[C]. PowerElectronics Specialist Conference, 2003: 1801-1806.

[9] 甘鴻堅，嚴仰光.高頻PWM 直-直變換的同步整流技術[J].電力電子技術,1998,32(4):105-108.Gan Hongjian, Yan Yangguang. Synchronous rectifierof high frequency DC-DC converters[J]. PowerElectronics, 1998, 32(4): 105-108.

[10]謝小高,張軍明,錢照明.基于新型同步整流驅動方案的綠色電源[J].電工技術學報，2007，22(3)：96-101.Xie Xiaogao, Zhang Junming, Qian Zhaoming. Agreen power supply based on a new synchronousrectification[J]. Transactions of China ElectrotechnicalSociety, 2007, 22(3): 96-101.

[11]錢照明，何湘寧.電力電子技術及其應用的最新發展(一)[J].中國電機工程學報,1997,17(6):361-366.Qian Zhaoming, He Xiangning. The recent developmentsof power electronics and its applications(1)[J].Proceedings of the CSEE, 1997, 17(6): 361-366.

[12]錢照明，董伯藩，何湘寧.電力電子技術及其應用的最新發展(二)[J].中國電機工程學報,1998,18(3):153-162.Qian Zhaoming， Dong Bofan， He Xiangning. Therecent developments of power electronics and itsapplications(II)[J]. Proceedings of the CSEE, 1998,18(3): 153-162.

[13]Van de Sype D M, De Gussems K, Van den BosscheA P. Experimental verification of the Z-domain modelfor digitally controlled converters[C]. Power ElectronicsSpecialists Conference, 2005: 2164-2170.

[14]Maksimovic D, Zane R. Small-signal discrete-timemodeling of digitally controlled PWM converters [J].IEEE Transactions on Power Electronics, 2007, 22(6):2552-2556.

[15]Maksimovic D, Zane R, Erickson R. Impact of digitalcontrol in power electronics[C]. Proceedings of ISPSD2004: 13-22.

[16]Corradini L, Mattavelli P. Analysis of multiplesampling technique for digitally controlled DC-DCconverters[C]. Power Electronics Specialists Conference,2006: 1-6.

[17]Corradini L, Mattavelli P. Modeling of multisampledpulse width modulators for digitally controlled DCDCconverters[J]. IEEE Transactions on PowerElectronics, 2008, 23(4): 1839-1847.

[18]Yao K, Meng Y, Xu P, et al. Design considerationsfor VRM transient response based on the outputimpedance[J]. IEEE Transactions on Power Electronics,2003, 18(6): 1270-1277.