基于支持向量機的物流量預測——以成都市為例
岳 輝,吳 波,單 翠,陳彥如
(1.中國中鐵二院工程集團有限責任公司,四川 成都 610031;2.西南交通大學經濟管理學院,四川 成都 610031)
0 引言
物流量預測作為物流系統規劃的重要環節,其預測精度直接影響到物流系統的分析建模、規劃布局等工作的科學性與有效性。因此,選取精度較高的預測方法,對提高物流規劃質量和運行效率具有重要的意義。
傳統的物流量預測方法,主要采用統計學預測方法、人工智能技術以及組合預測方法。武志惠等[1]采用Logistic模型確定區域物流業與區域經濟增長之間的數量關系,利用邊際分析和彈性分析計算出三大經濟圈物流業的單位增長帶來的區域經濟的貢獻。湯俊等[2]建立了基于最小二乘法的最優化模型(LaOR模型),該模型有效地降低了回歸模型的期望風險,但模型的泛化能力差。管春燕等[3]以武漢市區域物流量預測為實例,采用逐步回歸法建立模型,將影響程度大的變量依次納入模型中,提高了模型的運算效率。隨后Zhang G等[4]將人工神經網絡(ANN)用于預測,但人工神經網絡在解決復雜問題時容易陷入局部極小點。張曉磊[5]嘗試引用可以處理非線性、高復雜系統的人工神經網絡方法建立區域物流預測模型,但建模過程較為復雜。
支持向量機[6-7],簡稱SVM(Support Vector Ma?chine),是建立在統計學習理論上的機器學習方法,已經在實際應用中得到很大的發展。胡燕祝等[8]、Gao M[9]等考慮到SVM具有很強的迭代性能和非線性擬合功能的特點,將其用于物流需求預測。李春錦等[10]基于支持向量機模型預測方法,對我國石油需求預測進行了詳細研究。Smola A J等[11]揭示了支持向量機預測方法強大的泛化性能。Car?bonneau R等[12]詳細研究了自適應性的機器學習過程,并與傳統預測方法,如趨勢預測、移動平均等方法相比較,驗證了支持向量機良好的預測性能。Lu Shan等[15]證明應用于支持向量機在非線性類問題和功能評價方面的適用性。楊雯斌[14]研究了在大規模數據情況下支持向量機的應用,再次證明了支持向量機泛化能力的強大。
綜上所述,國內外學者對物流量預測進行了較多的分析研究,給出了具有重要參考價值的成果。不過部分研究方法存在著泛化能力弱、建模復雜、易陷入局部最優等局限。由于支持向量機理論具有強大的泛化能力,本文以成都市為背景,通過對該市的物流量預測實證分析,檢驗該方法的有效性。
1 支持向量機理論概述
在統計學理論中,學習機的風險有兩類:經驗風險和期望風險。經驗風險一般指在模型建模時,對已有樣本數據的擬合精度,而期望風險指模型的實際擬合精度。當樣本容量很大且樣本數據值無異常時,經驗風險和期望值風險的差異較小,但當樣本為小樣本或者數據包含異常數據時,難以保證傳統學習的泛化能力。而支持向量機基于結構化風險最小化的思想卻很好地解決此類問題。支持向量機的模型如下:
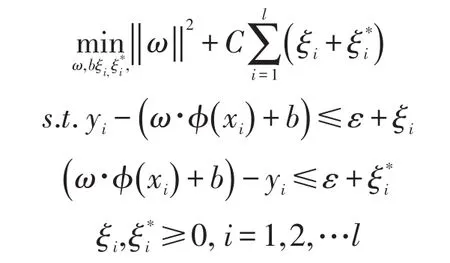
式中:目標函數用來控制泛化能力;約束條件用來減少經驗風險;C為懲罰函數,用來控制樣本誤差和機器泛化能力之間的平衡。
為了避免維數災難,支持向量機將原來空間維度非線性問題轉化為高維度線性問題,而高維度空間涉及到原樣本的之間內積運算,這種內積只要找到滿足Mercer條件下的核函數K(xi,xj),就會對應空間某個內積,如圖1所示。
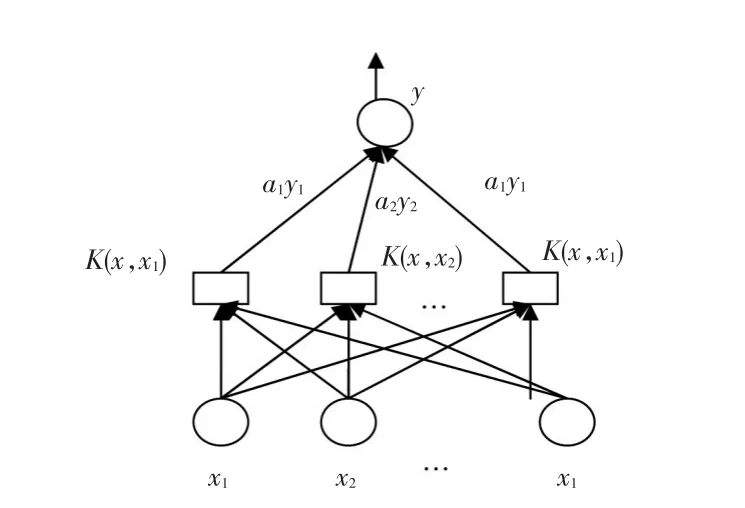
圖1 核函數
2 基于支持向量機的物流量預測模型建立
根據支持向量回歸機原理及物流量相關理論,本文建立了基于支持向量機的物流量預測模型,具體步驟如下。
2.1 確定物流量影響指標
首先需確定影響物流量的主要指標。為了保證物流量預測的準確性和科學性,通過相關性分析,本文選取的物流量影響指標有:第一產業產值(億元)、第二產業產值(億元)、第三產業產值(億元)、社會消費品零售總額(億元)、進出口貿易總額(億美元)、城鎮居民可支配收入(百元)、農村居民可支配收入(百元)以及貨運量(千萬噸)。
2.2 數據預處理
由于原始數據量綱不同,為了避免數據處理過程中由于數量級不同而影響預測結果,需要對原始數據進行統一的量綱處理。
2.3 構建模型
將已知樣本分為訓練樣本與測試樣本,對不同的訓練樣本進行反復訓練,根據訓練結果選擇最佳的模型參數,然后構造支持向量機模型并求解最優化問題。
3 成都市物流量預測實證分析
本文采用的支持向量機軟件為Libsvm—2.88。下面將以成都市為例,進行物流量預測。由于目前沒有直接的物流作業量統計指標,如倉儲量、配送量、流通加工量等統計值,并考慮到運輸是物流中最重要的環節,且在一定程度上運輸需求能反映物流需求,因此,本文選取貨運量作為物流量指標進行預測。
3.1 數據指標收集
以成都市貨運量為被解釋變量,指標統計數據如表1所示(數據來源于成都市1996—2010年統計年鑒)。

表1 成都市物流需求預測指標原始數據表

表1 (續)
3.2 數據預處理
按照Libsvm—2.88軟件輸入格式的規范,將原始數據轉化為表2所示的數據格式,同時建立訓練數據樣本和測試數據樣本。

表2 規范數據格式
3.3 支持向量機參數選擇
本文選擇ε-SVM回歸模型,核函數選擇RBF。利用gridregression.py包對模型參數進行優化,獲得的最佳參數分別為:C=64.0,g=0.125,p=0.5。
3.4 求解結果及數據分析
3.4.1 支持向量機回歸模型求解
在DOS窗口中,輸入svm-train-s 3-t 2-c 64.0-g 0.125-p 0.5 data.txt,從而獲得data.txt.mod?el,利用訓練的模型和測試的數據可以獲得相應的輸出值在out.txt中。
3.4.2 數據分析
由out.txt可以輸出通過支持向量機預測得到的2008—2010年的貨運量結果,表3~表5給出了不同試驗組得到的結果及與2008—2010年實際貨運量的對比。為了反映訓練數據樣本多寡對支持向量機預測結果的影響,分別選取2003—2007年、2002—2007年、…、1996—2007年作為訓練樣本中的第1組、第2組、…、第8組數據。
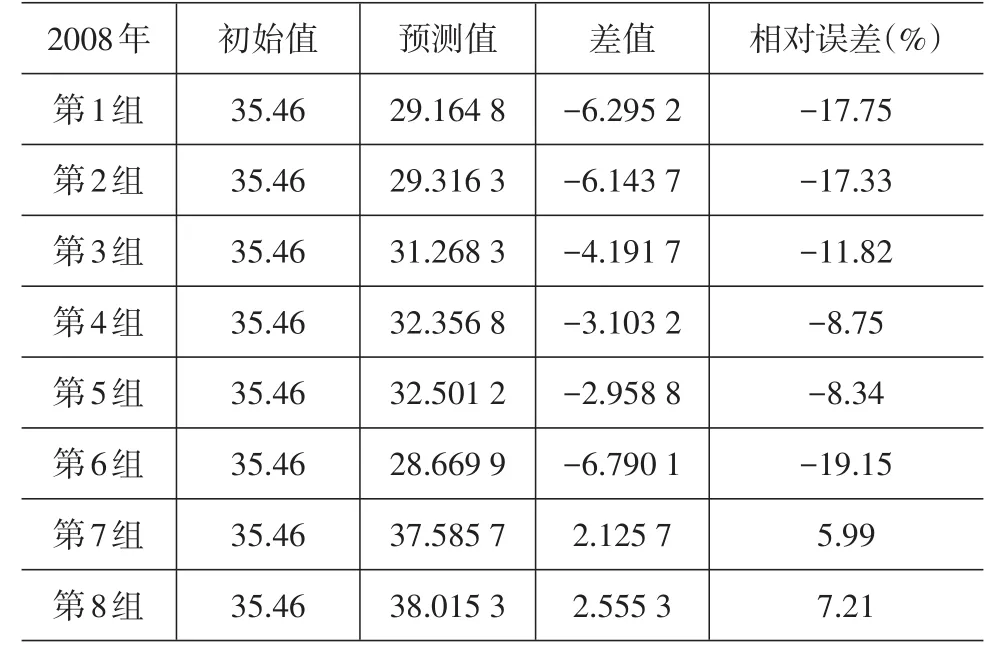
表3 向量機預測值和2008年實際值對比

表4 向量機預測值和2009年實際值對比
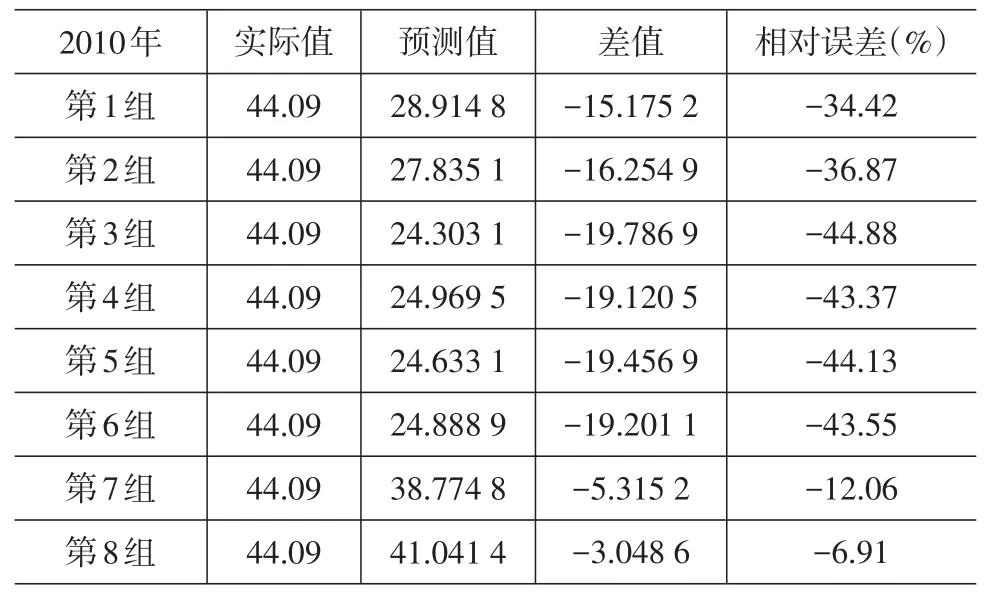
表5 向量機預測值和2010年實際值對比
從表3、表4、表5中可以看出,第1組的預測數據相對誤差達到了近20%,但隨著訓練樣本量的增加,整體的相對誤差呈減少趨勢,2008年、2009年分別在第7組及2010年在第8組的相對誤差達到最小值:5.99%、3.82%、-6.91%,誤差回落的速度較快。
為了驗證支持向量機的預測效果,本文運用多元線性回歸,采用同樣的分組對2008—2010年之間貨運量預測并與實際值進行對比,結果如表6~表8所示。
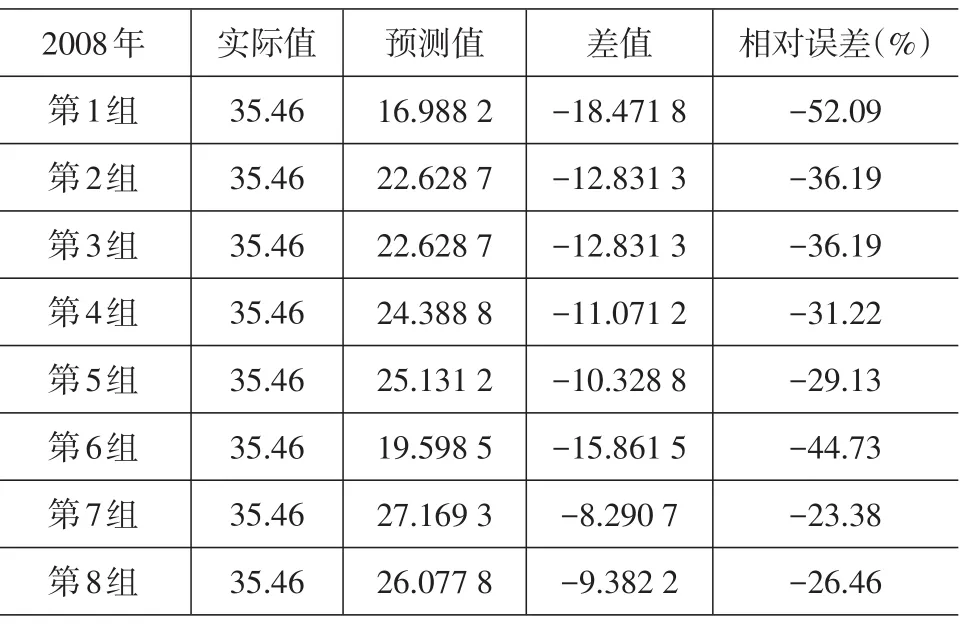
表6 回歸預測值和2008年實際值對比
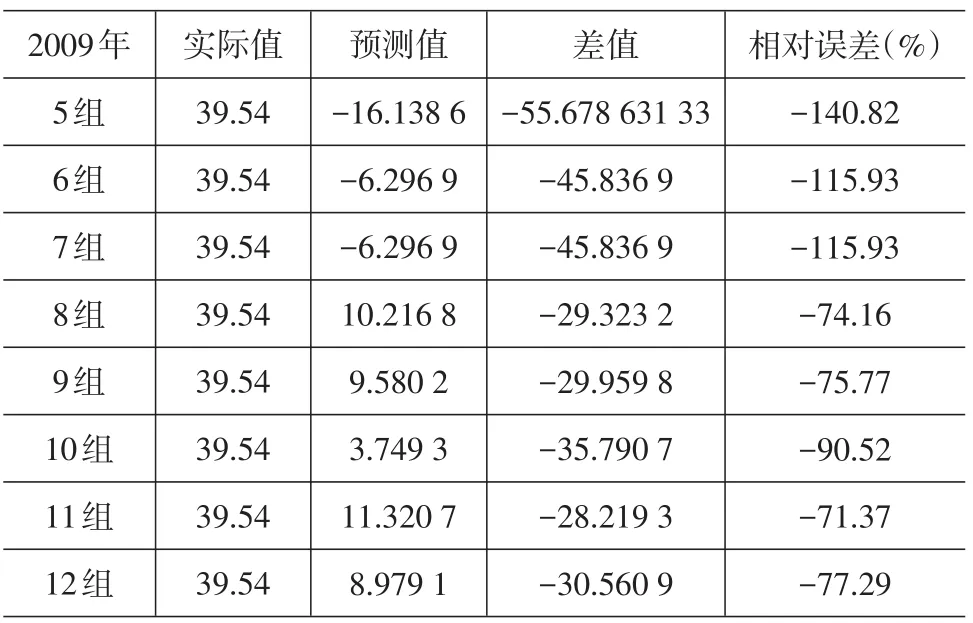
表7 回歸預測值和2009年實際值對比
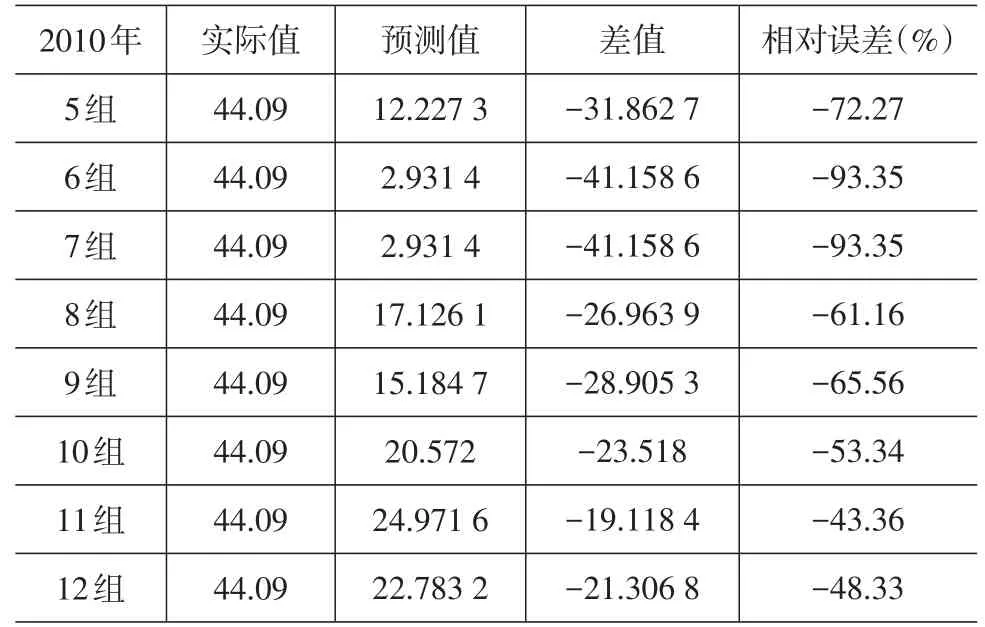
表8 回歸預測值和2010年實際值對比
從表6~表8可以發現,通過多元線性回歸得到預測值的相對誤差總體偏大,雖然隨著數據量的增加有明顯的回落趨勢,但最小的相對誤差達-23.38%,最大竟達到-140.82%,與支持向量機的預測效果差距比較明顯。
4 結語
本文考慮到支持向量機的預測優勢,將其用于成都市物流量預測中。結果表明,隨著訓練樣本數據的增加,預測值與實際值的相對誤差呈減少趨勢,誤差回落的速度較快,最小誤差為3.82%。此外選取多元線性回歸模型對相同的樣本進行預測,結果表明該模型預測值與實際值相對誤差總體偏大,雖然隨著數據量的增加有明顯的回落趨勢,但最小的相對誤差達到-23.38%,最大達到-140.82%,與支持向量機的預測效果差距明顯,證明了支持向量機用于物流量預測的有效性。
[1]武志惠,虞巧穎,申金升.三大經濟圈的物流業對區域經濟增長的實證分析[J].北京交通大學學報:社會科學版,2008,7(1):43-47.
[2]湯俊,肖建華.區域物流需求預測的LaOR方法[J].商業研究,2007,365(9):32-35.
[3]管春燕,蘇建美.基于逐步回歸分析的武漢區域物流量預測[J].企業導報,2012(16):133-135.
[4]Zhang G,Eddy Patuwo B,Y Hu M.Forecasting with artifi?cial neural networks:The state of the art[J].International journal of forecasting,1998,14(1):35-62.
[5]張曉磊.ANN分析在廣西區域物流需求預測中的應用[J].物流工程與管理,2011,33(3):58-60.
[6]Cristianini N,Shawe-Taylor J.支持向量機導論[M].北京:電子工業出版社,2004.
[7]張學工.關于統計學習理論與支持向量機[J].自動化學報,2000,26(1):32-41.
[8]胡燕祝,呂宏義.基于支持向量回歸機的物流需求預測模型研究[J].物流技術,2008,27(5):66-68.
[9]Gao M,Feng Q.Modeling and Forecasting of Urban Logis?tics Demand Based on Support Vector Machine[C]//Knowl?edge Discovery and Data Mining,2009.WKDD 2009.Sec?ond International Workshop on.IEEE,2009:793-796.
[10]李春錦,閆云聚.基于支持向量機的中國石油需求量預測研究[J].西安石油大學學報:自然科學版,2013,28(2):103-106.
[11]Smola A J,Sch?lkopf B.A tutorial on support vector re?gression[J].Statistics and computing,2004,14(3):199-222.
[12]Carbonneau R,Laframboise K,Vahidov R.Application of machine learning techniques for supply chain demand forecasting[J].European Journal of Operational Research,2008,184(3):1140-1154.
[13]Lu S,Han H,Dong J.Adaptability of SVR Time Series Analysis Used in Forecasting of Logistics Demand[C].In?ternational Conference on Transportation Engineering,2007:1298-1303.
[14]楊雯斌.支持向量機在大規模數據中的應用研究[D].上海:華東理工大學,2013.

